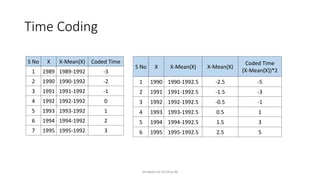
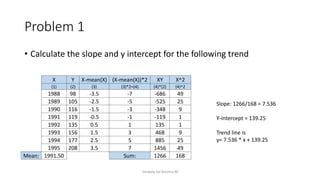
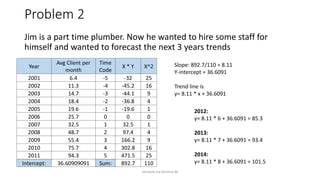
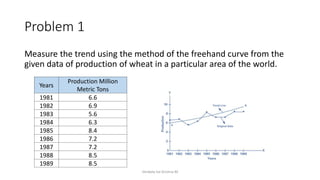
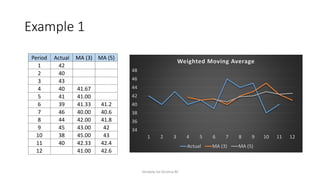
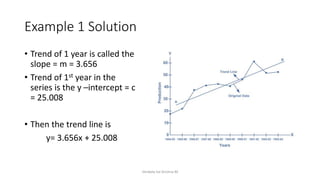
The document discusses forecasting in time series analysis, defining various types of variations such as secular trends, cyclical fluctuations, seasonal variations, and irregular variations. It emphasizes the importance of using historical data to project future trends, providing methods for fitting linear trends and estimating trends, including the least-squares method, moving averages, and freehand curves. The author illustrates these concepts through practical examples and calculations, showcasing how to determine slope and intercept for trend lines.