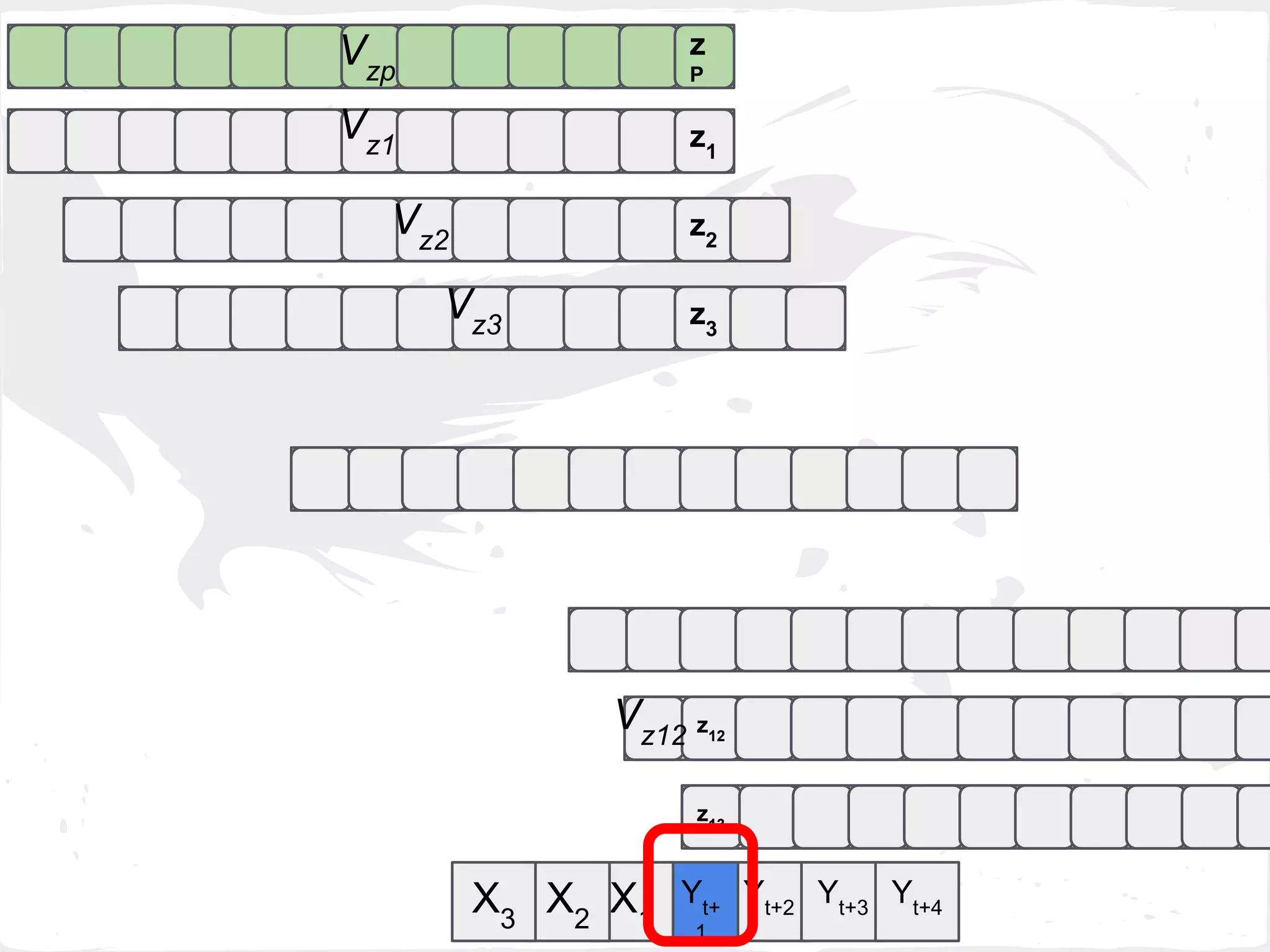
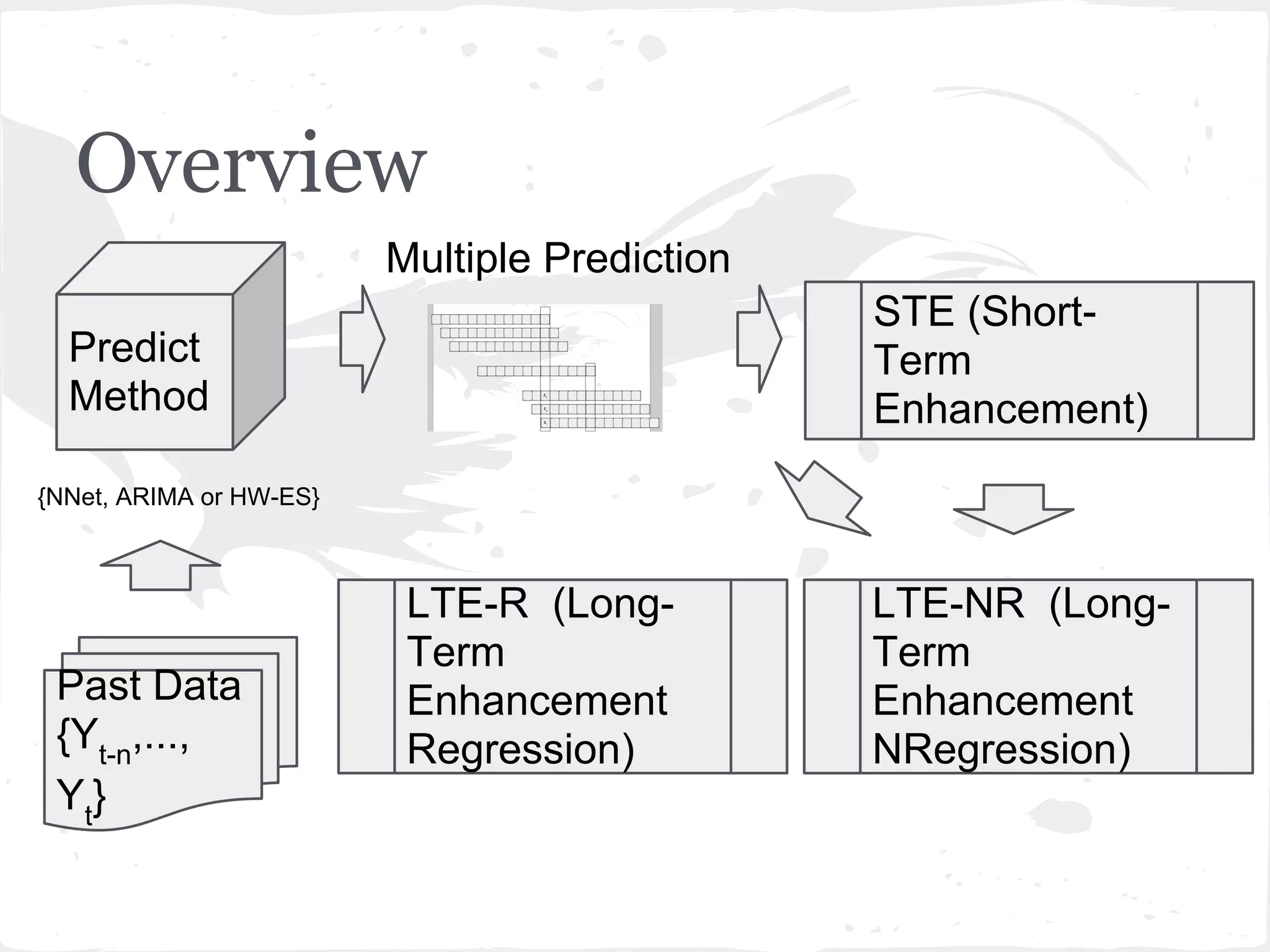
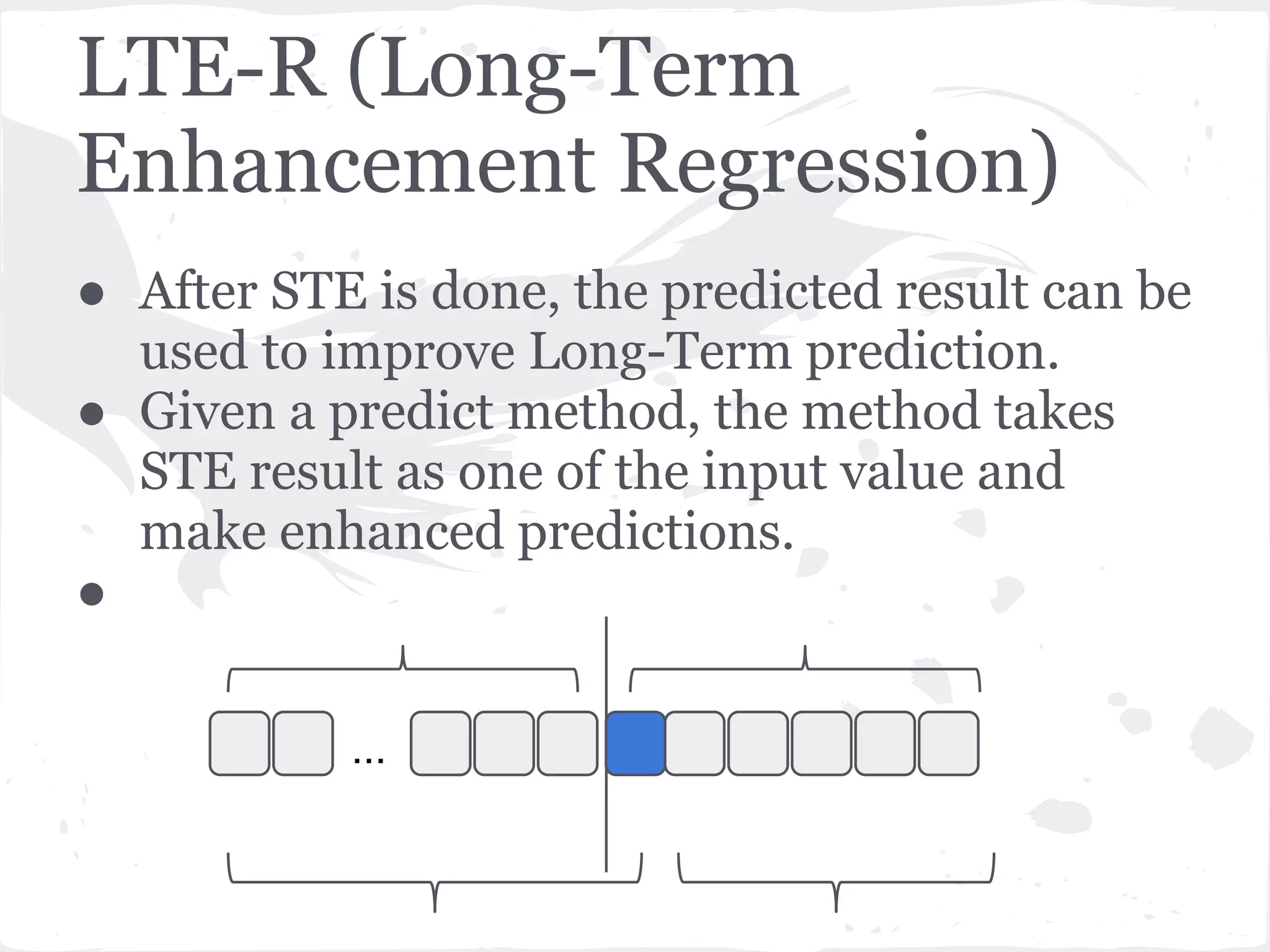
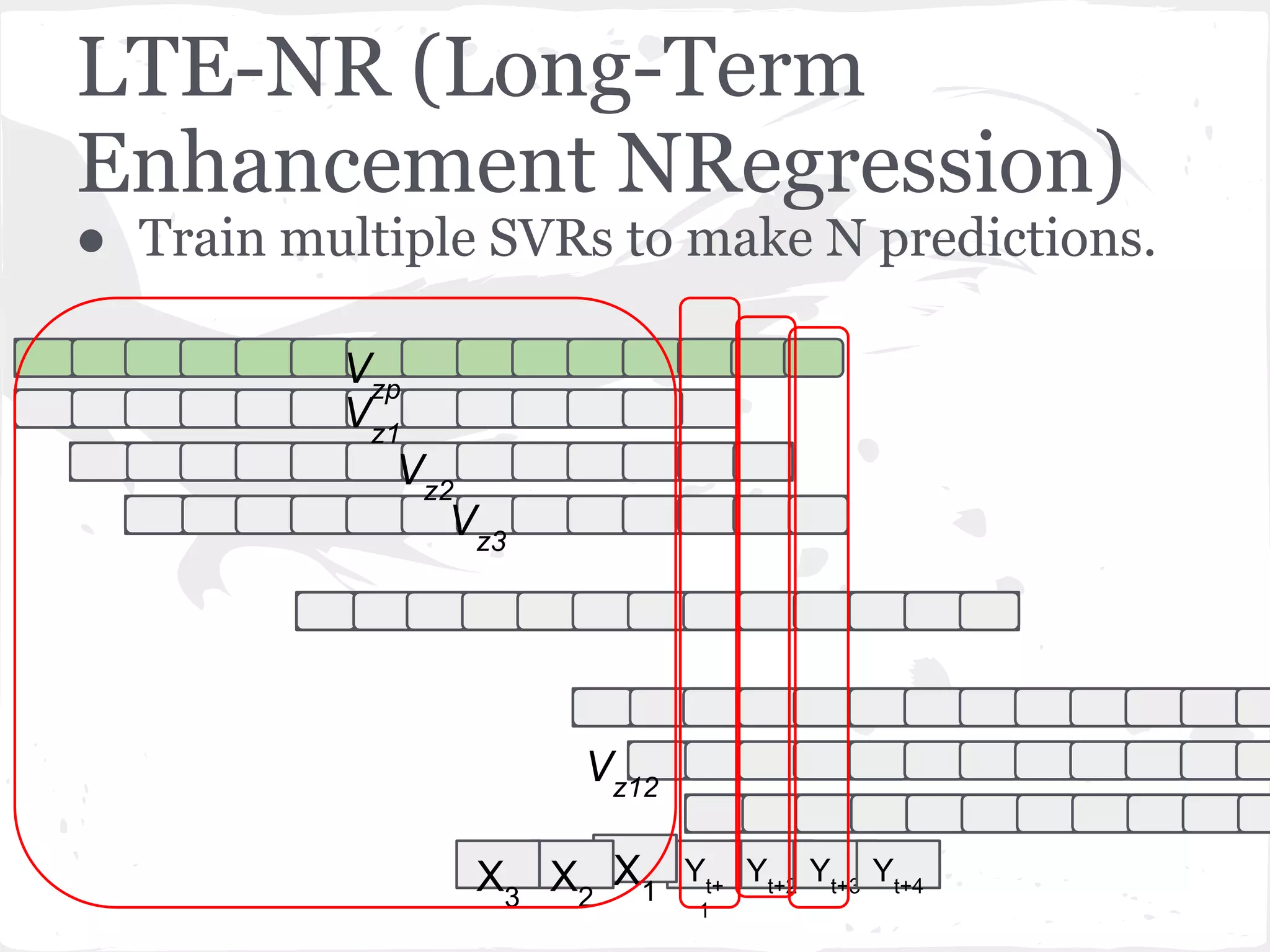
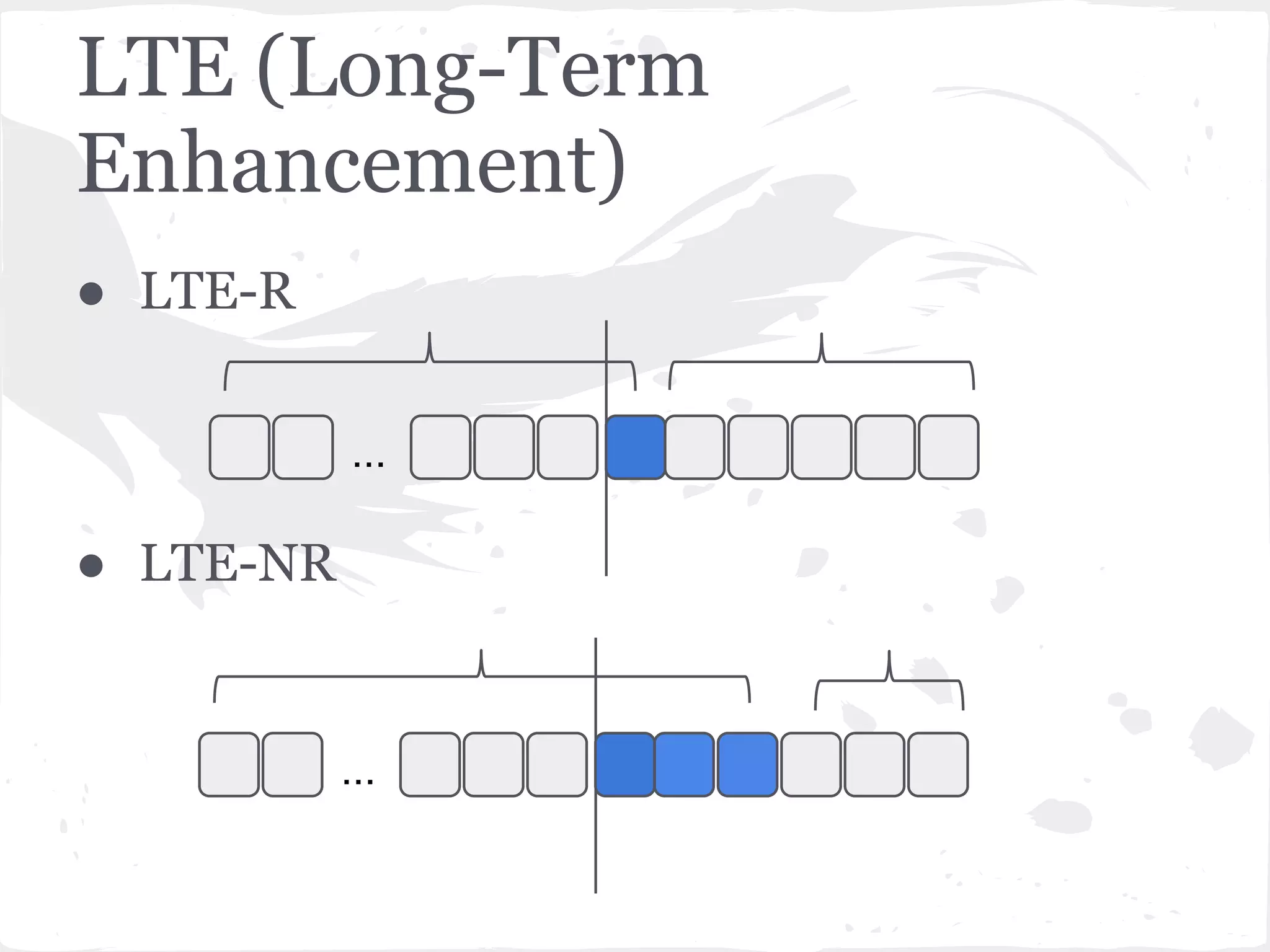
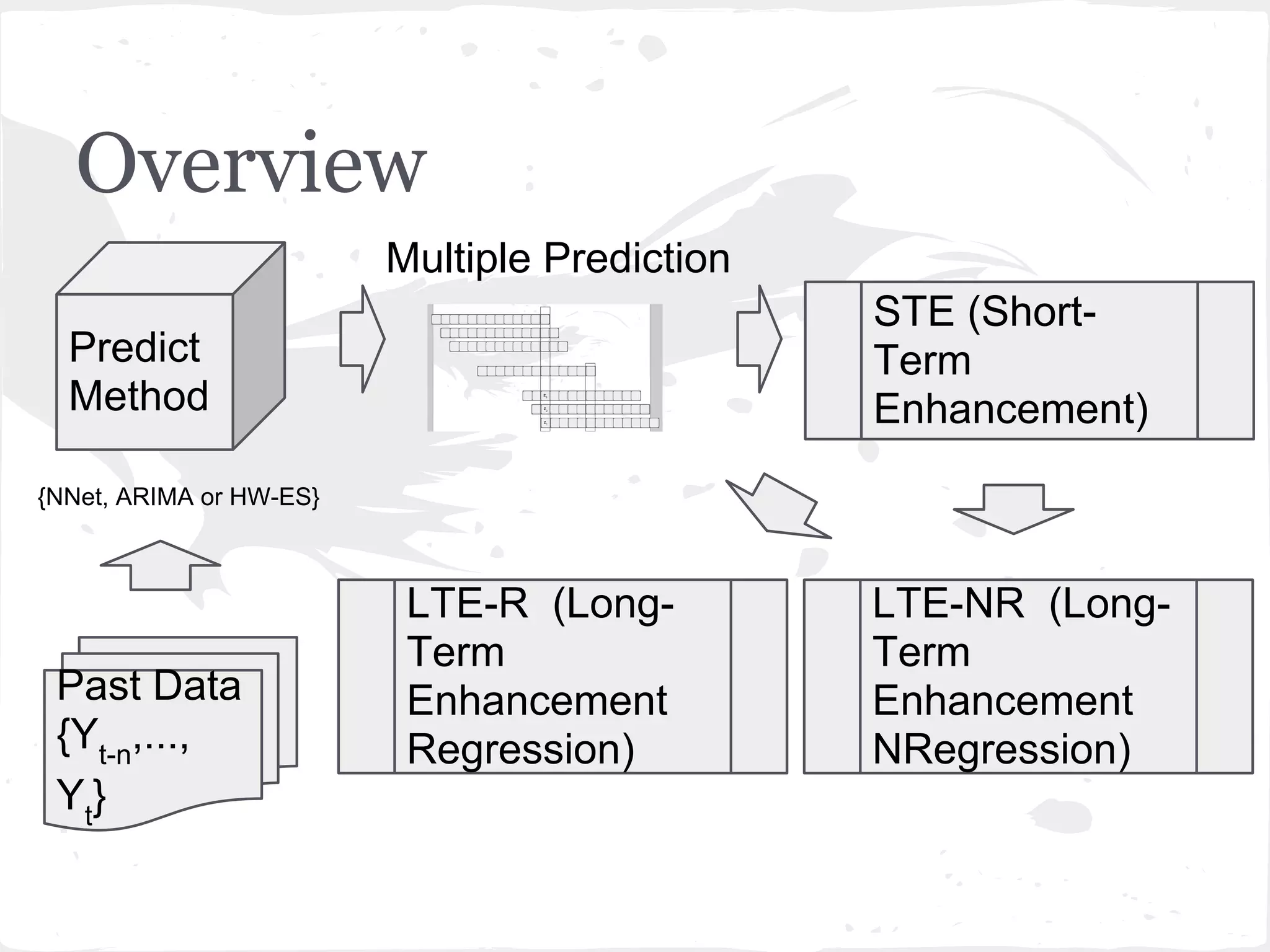
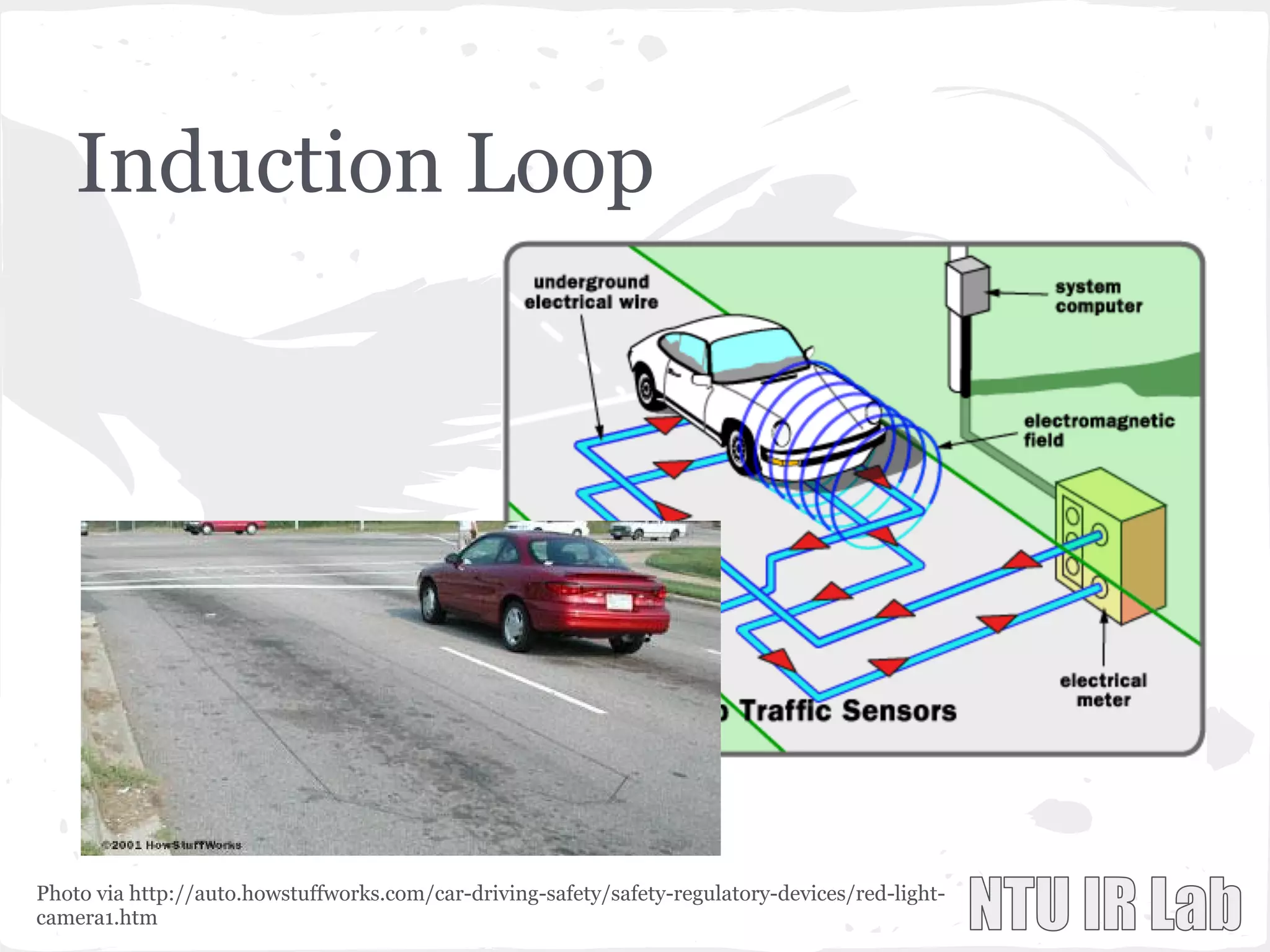
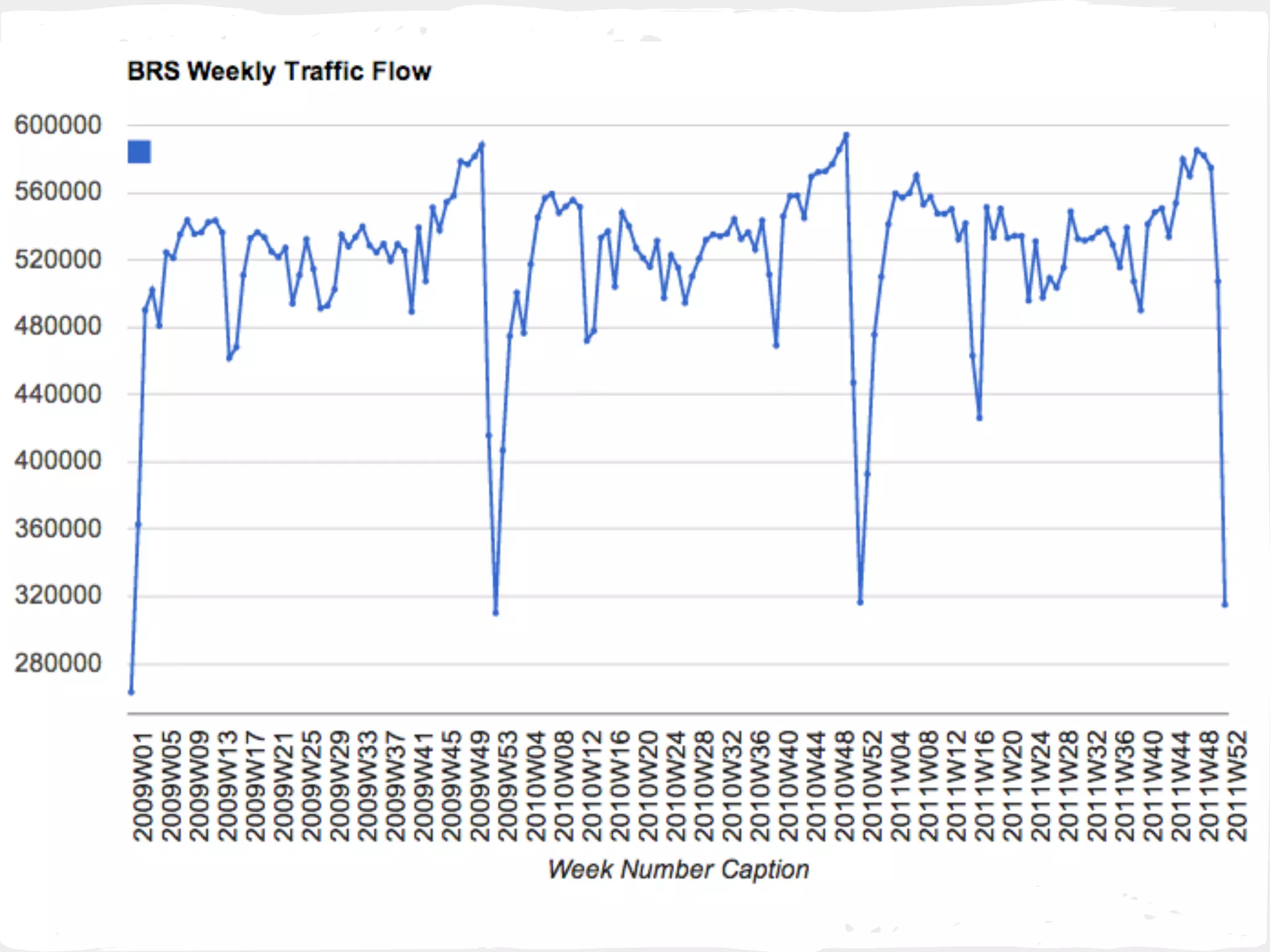
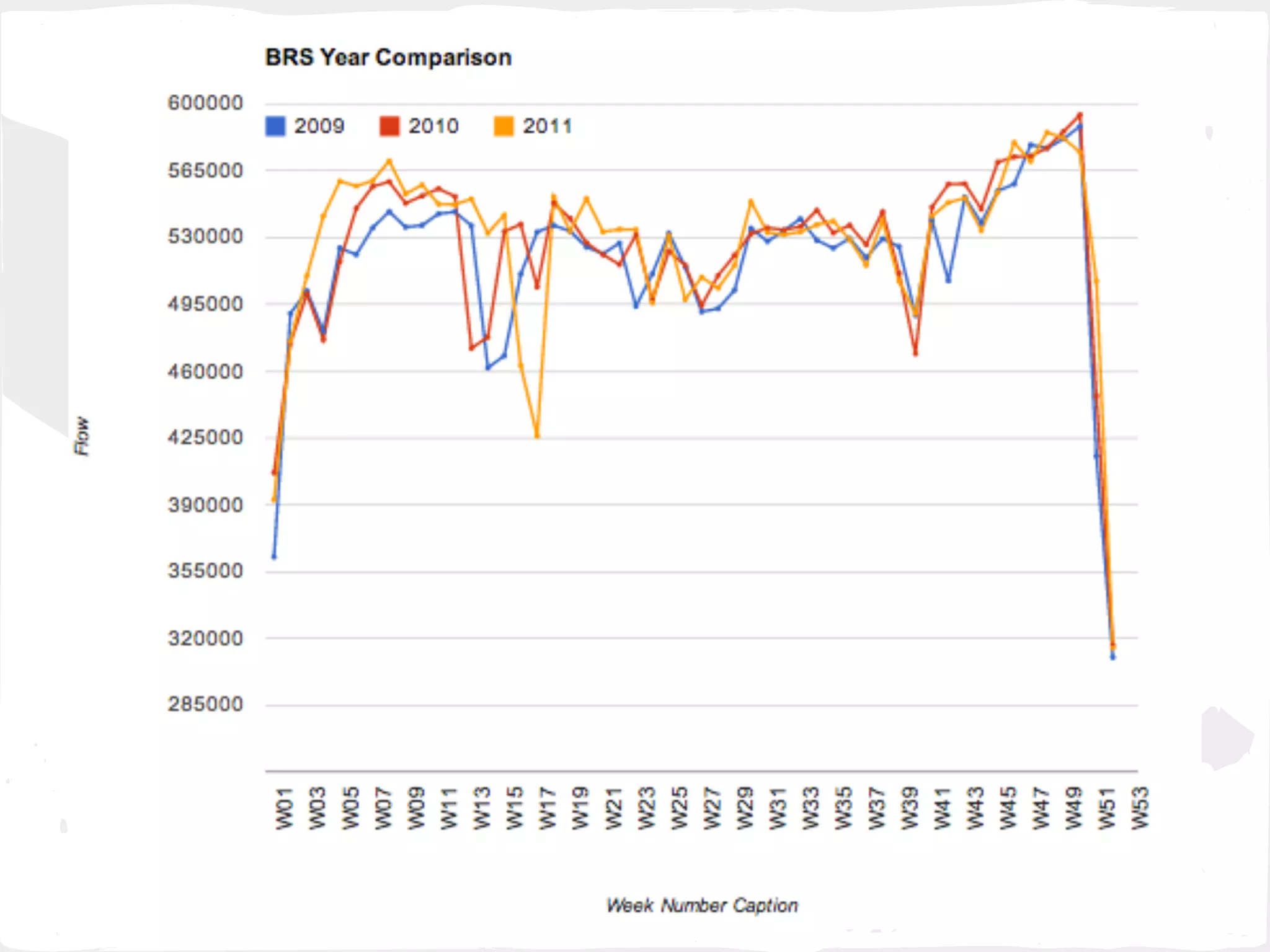
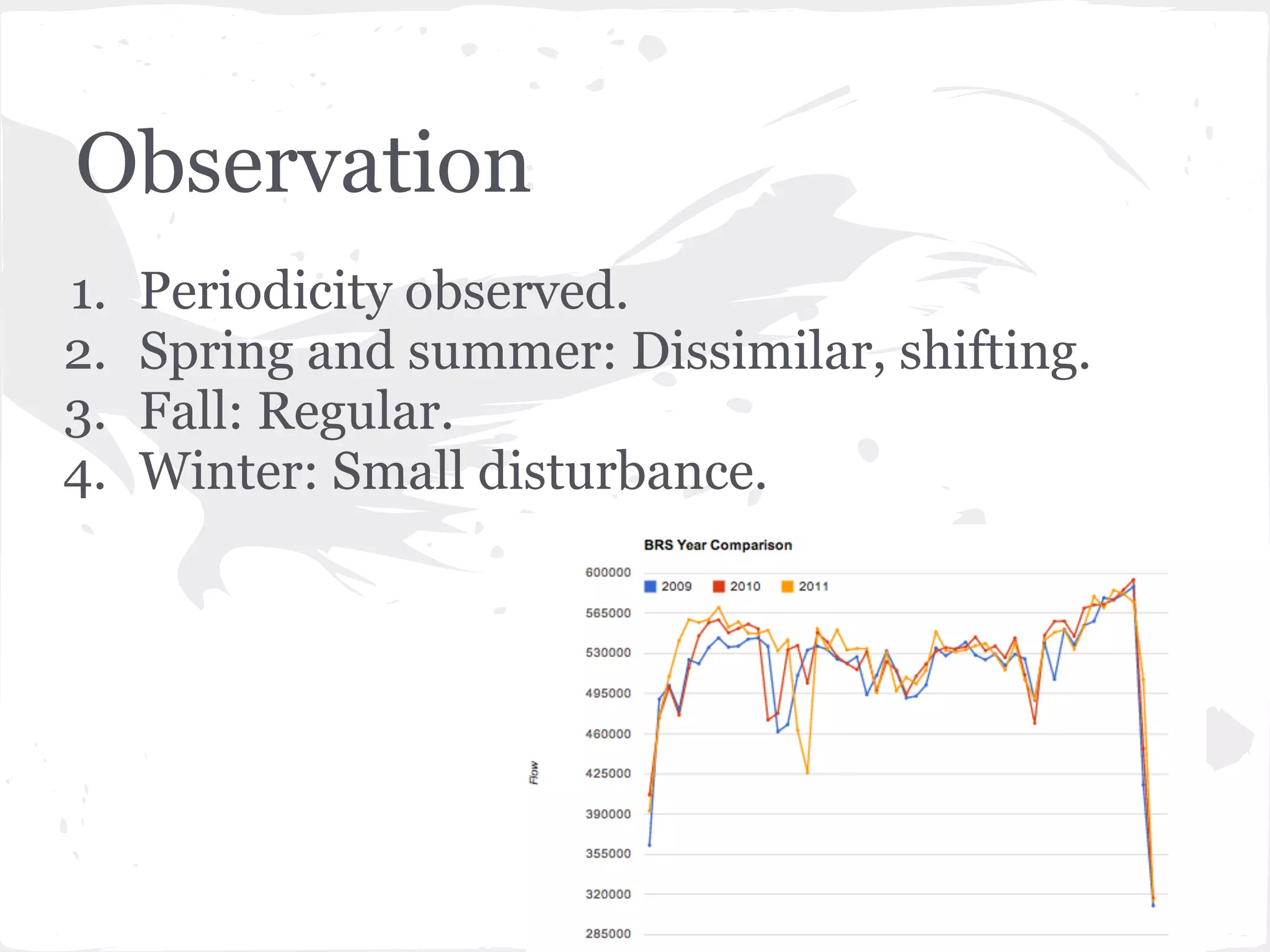
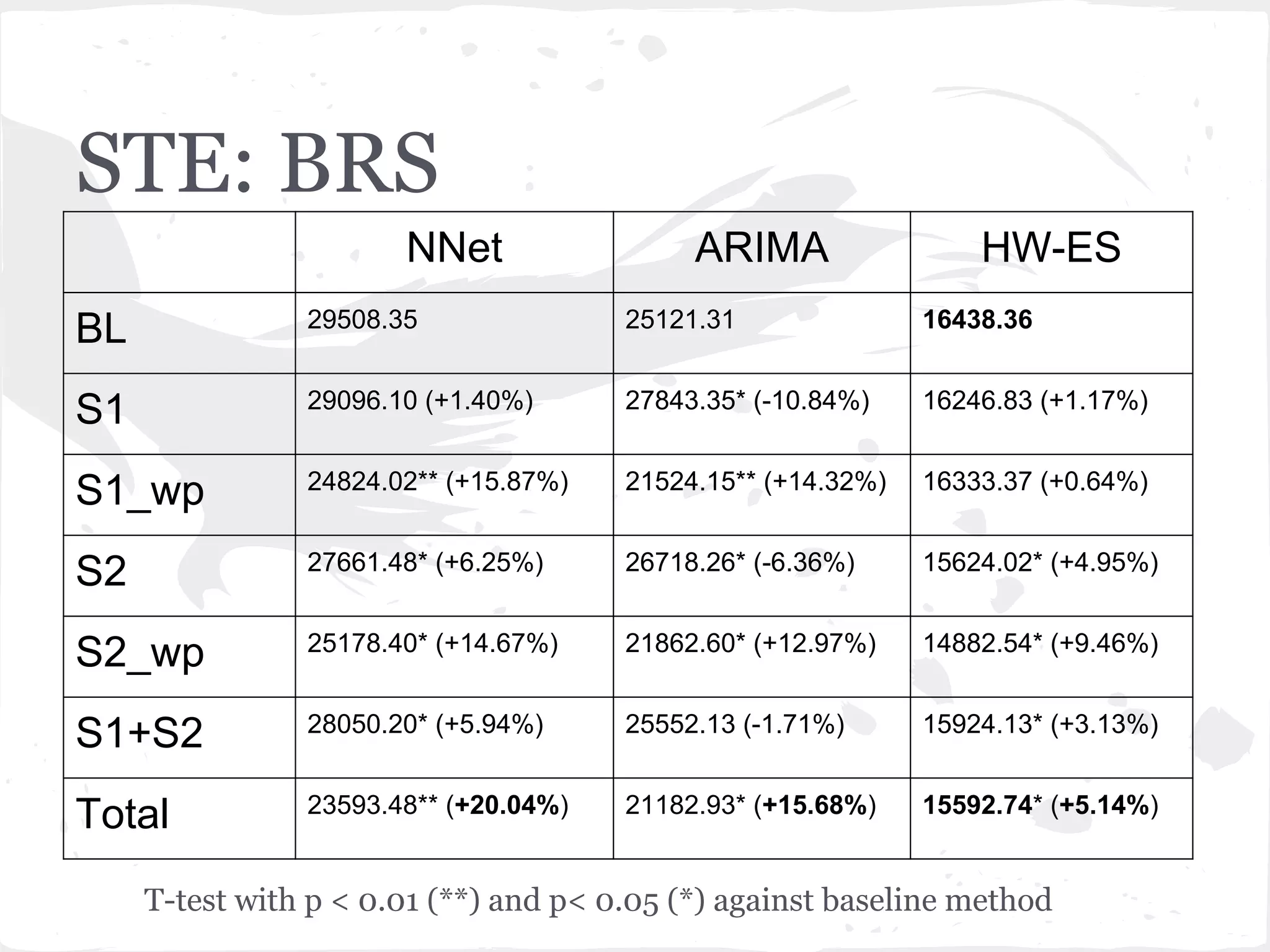
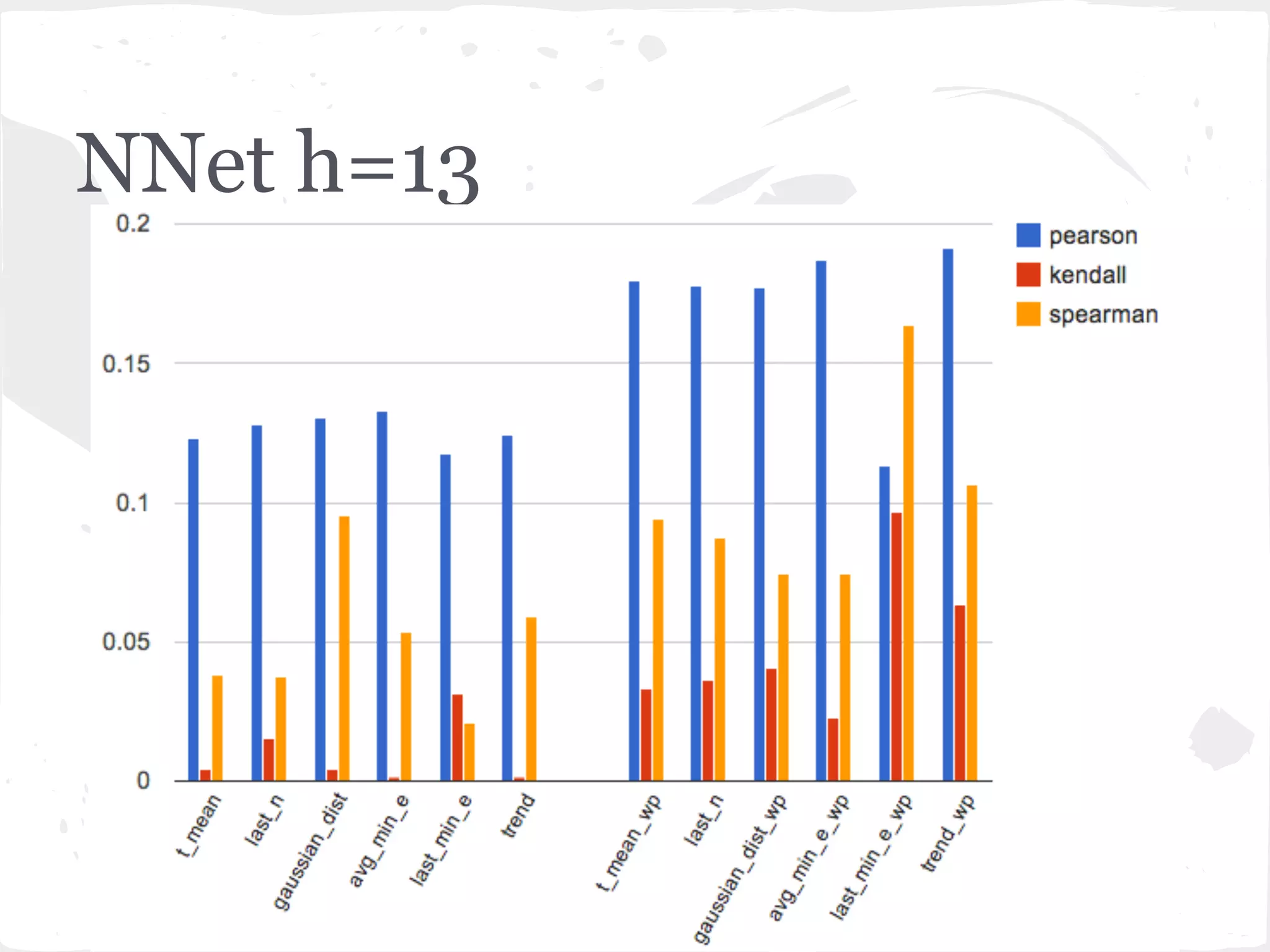
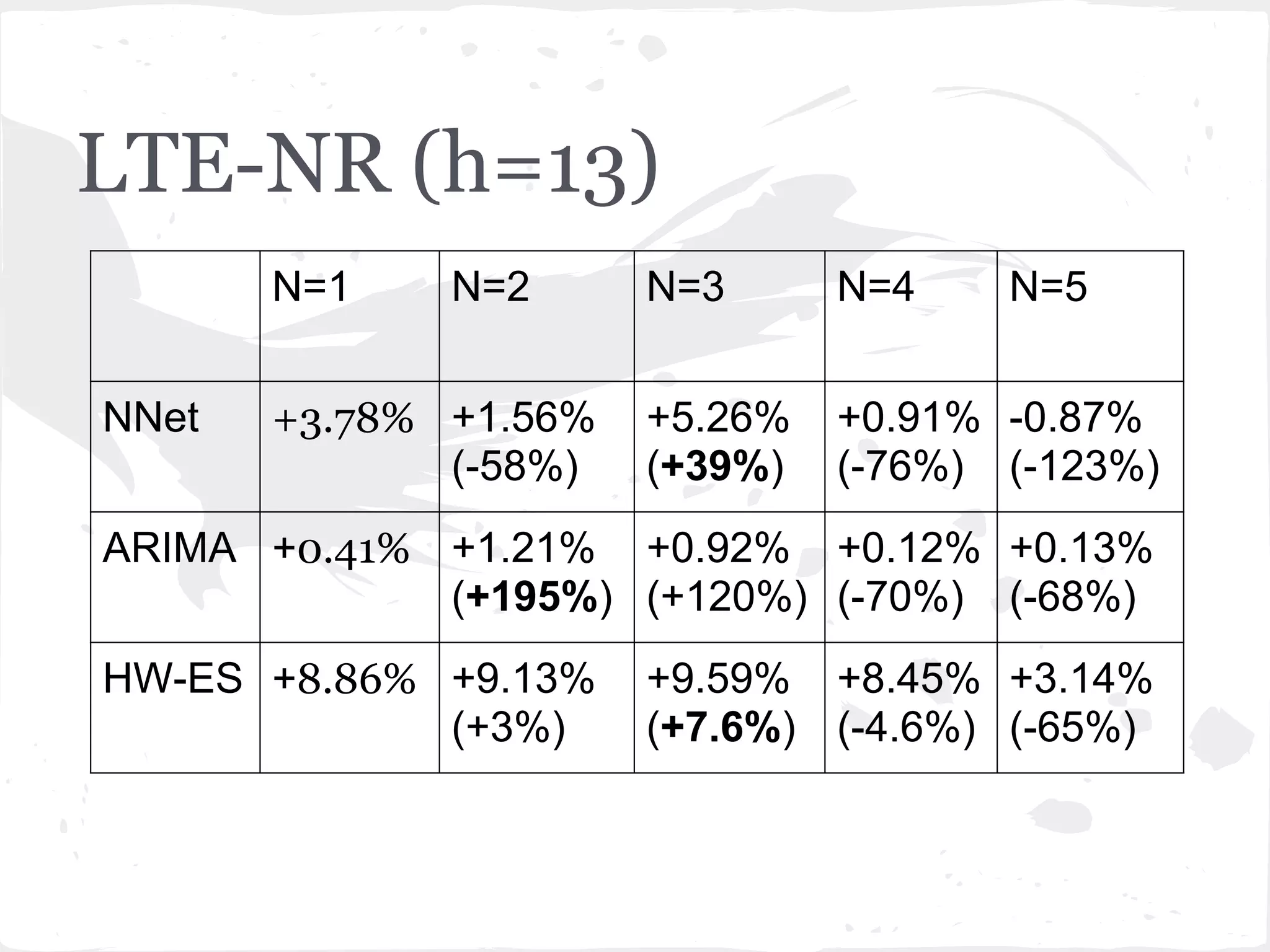
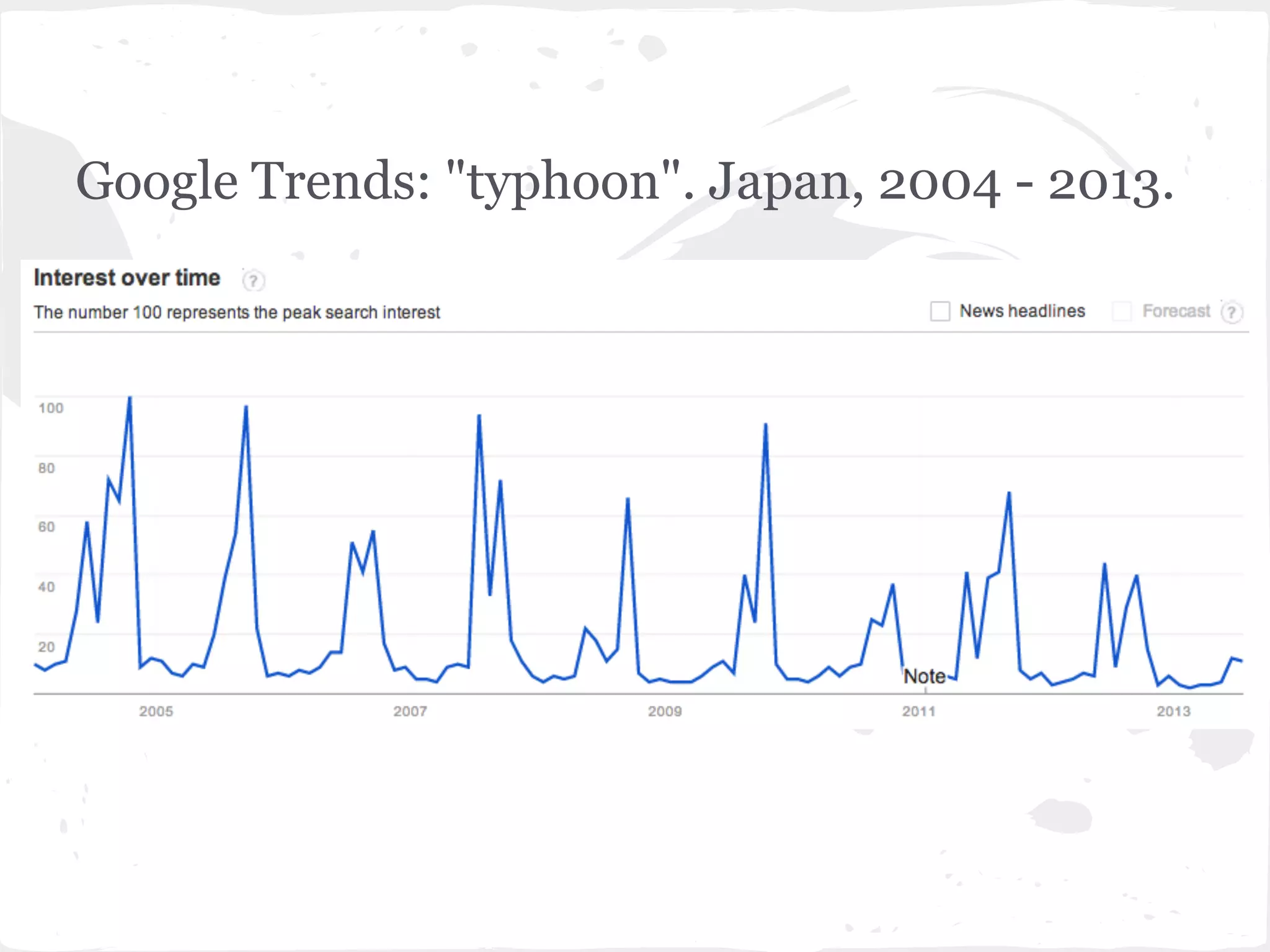
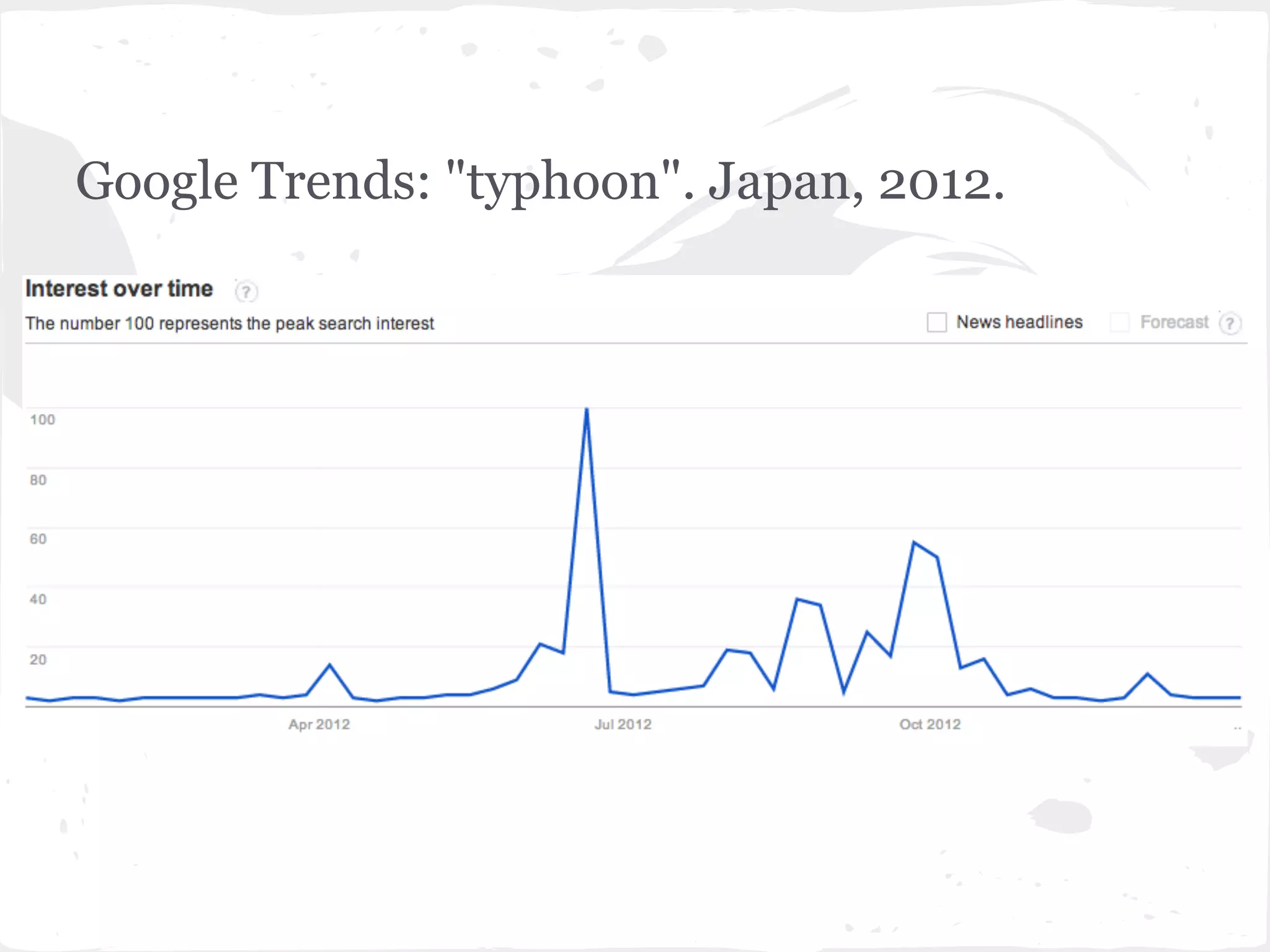
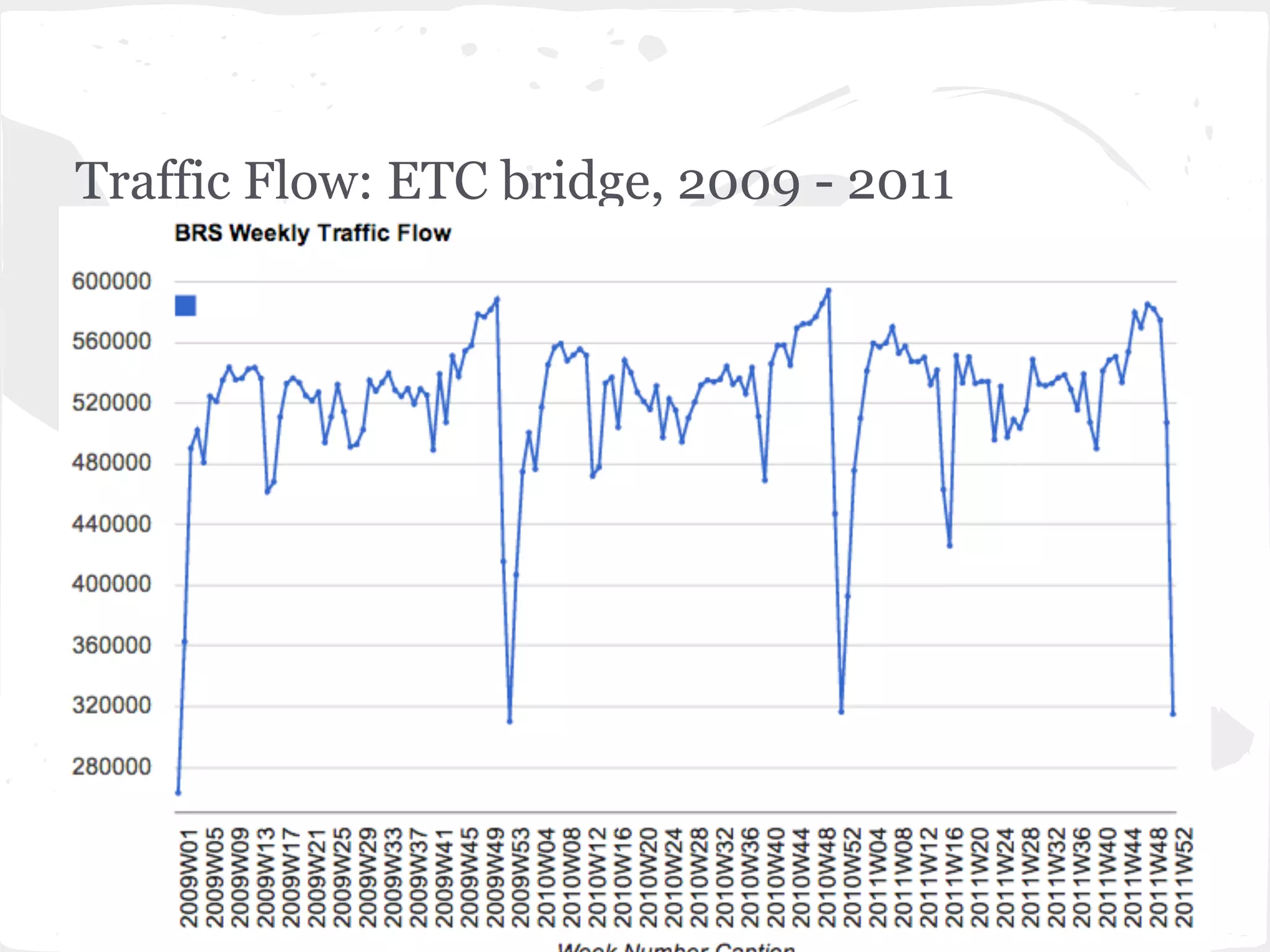
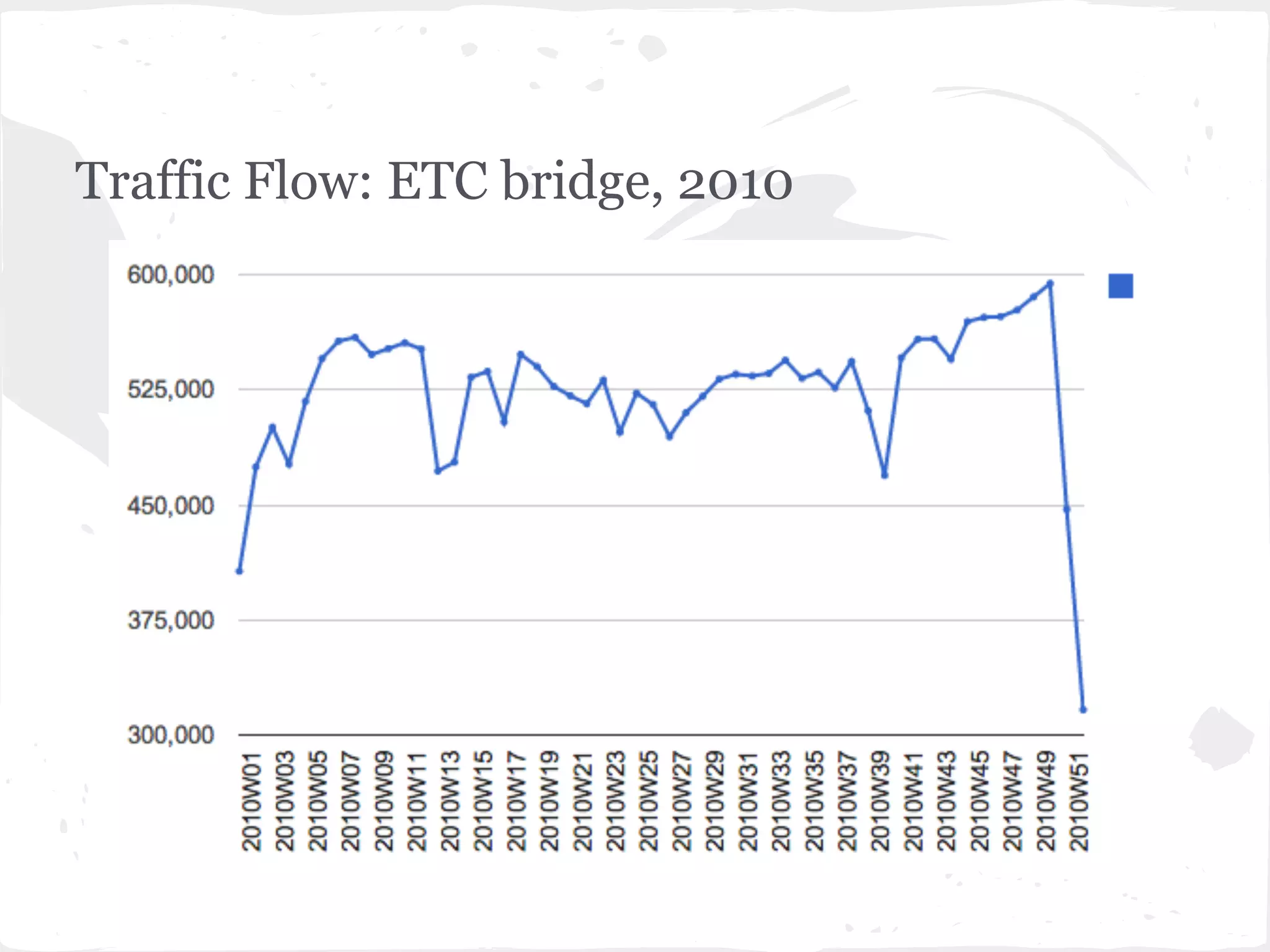
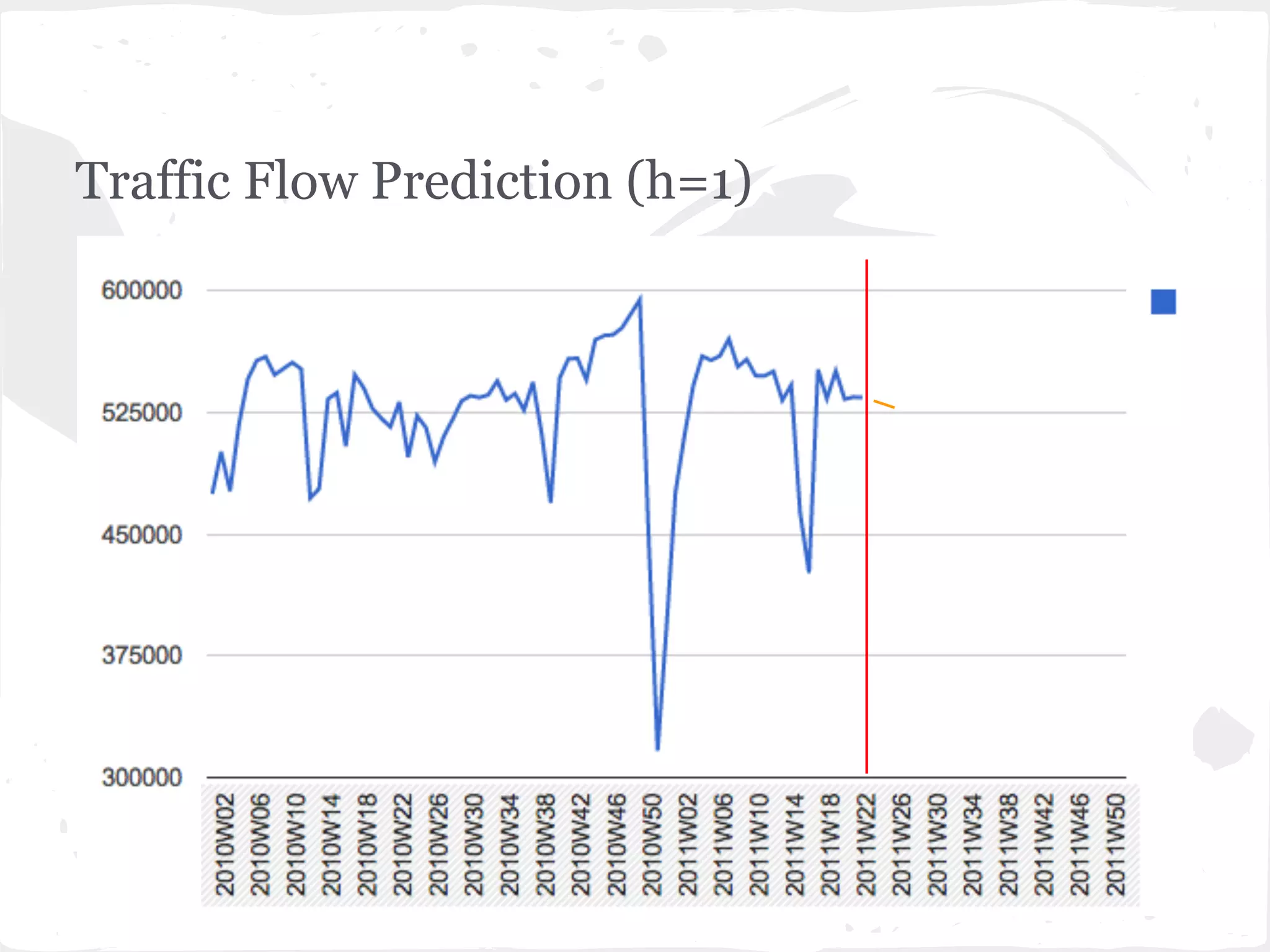
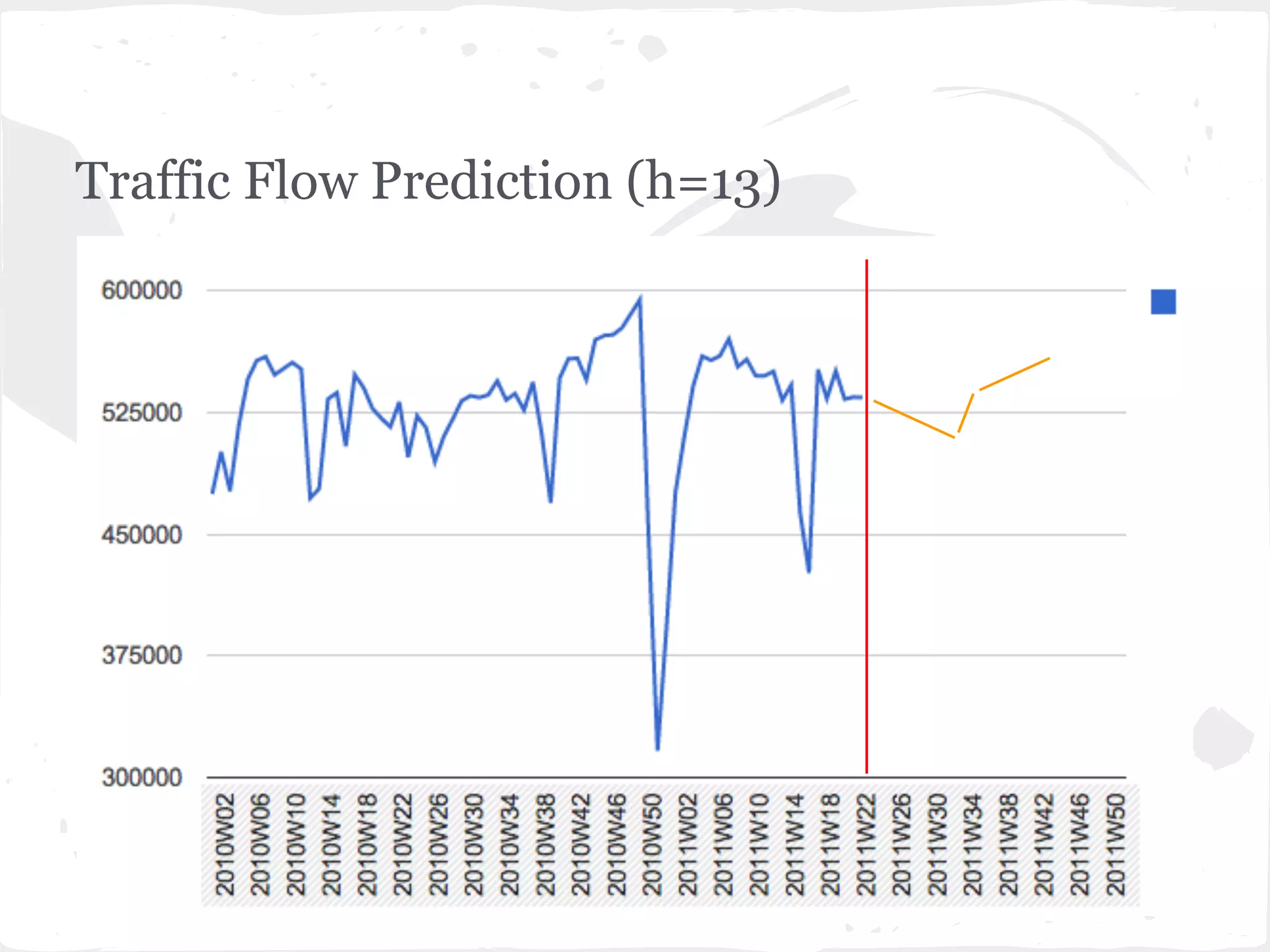
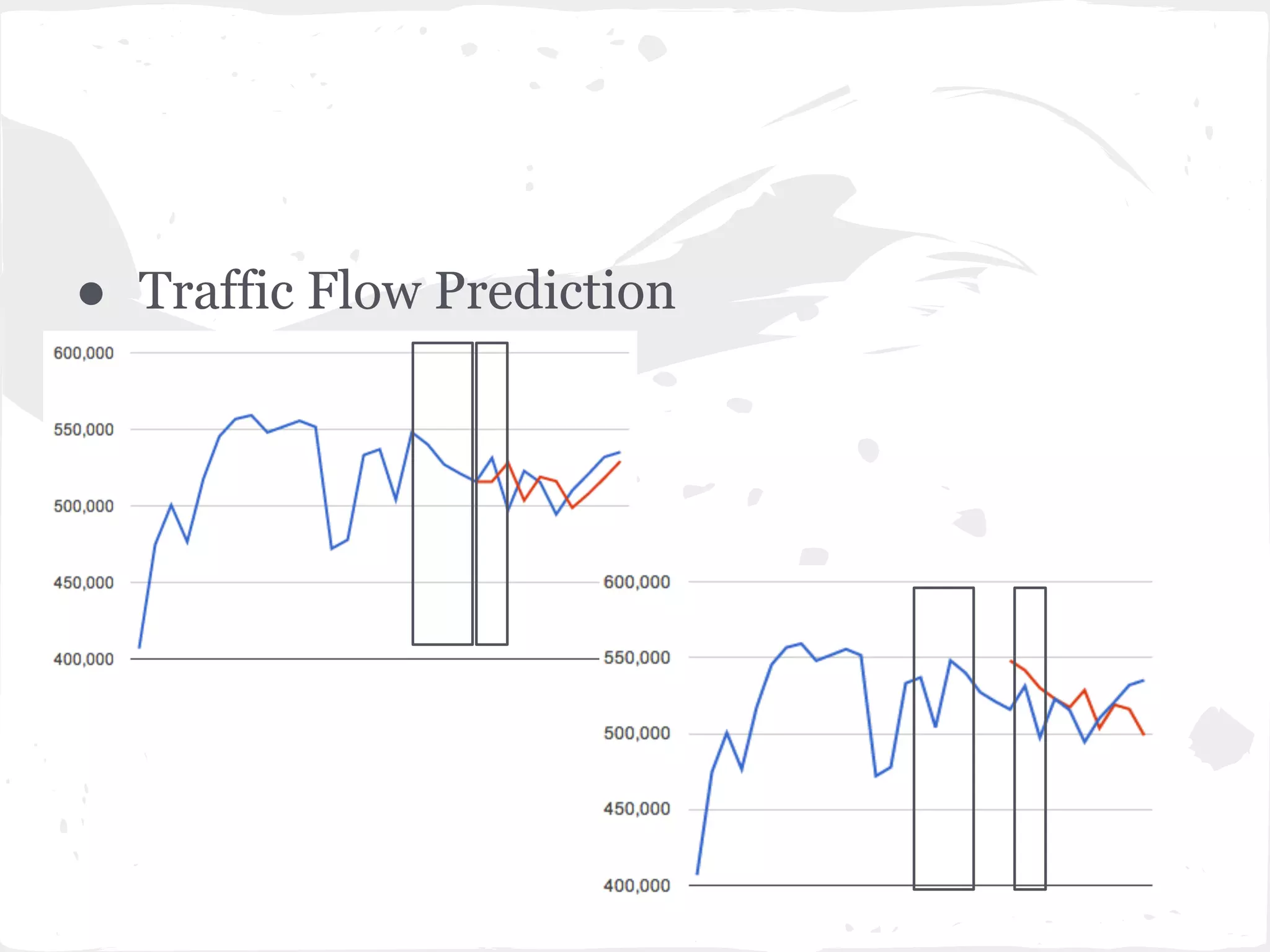
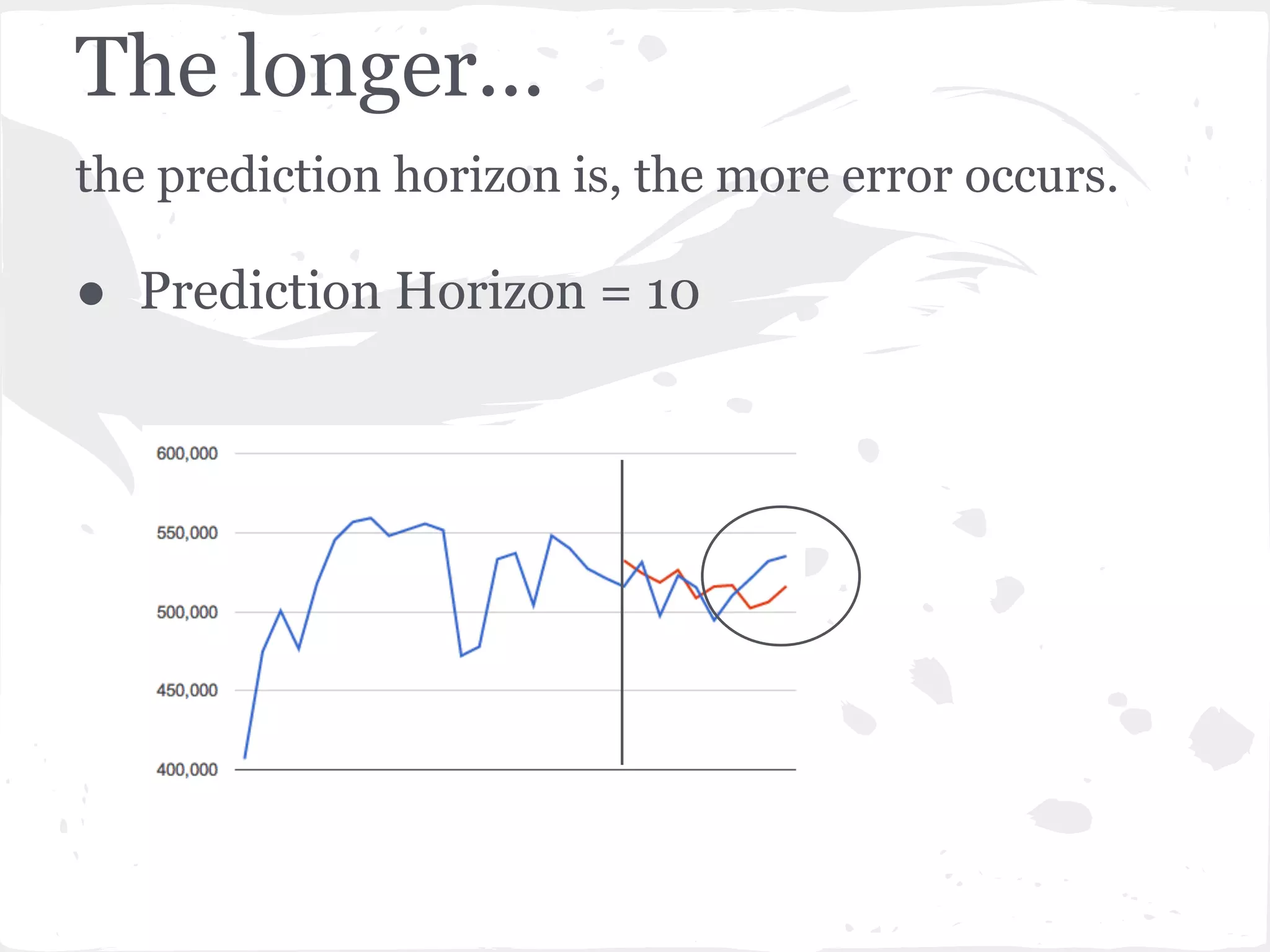
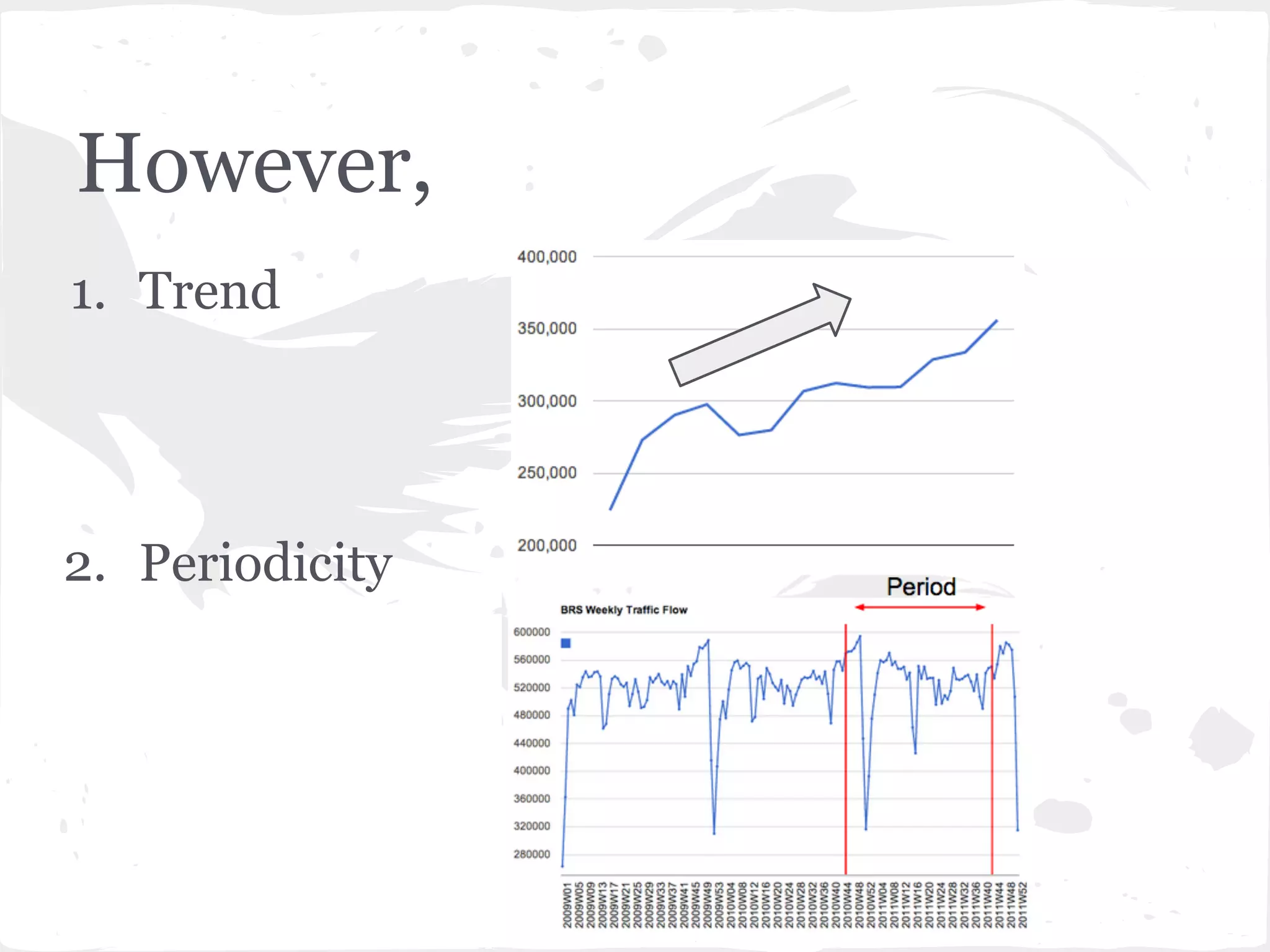
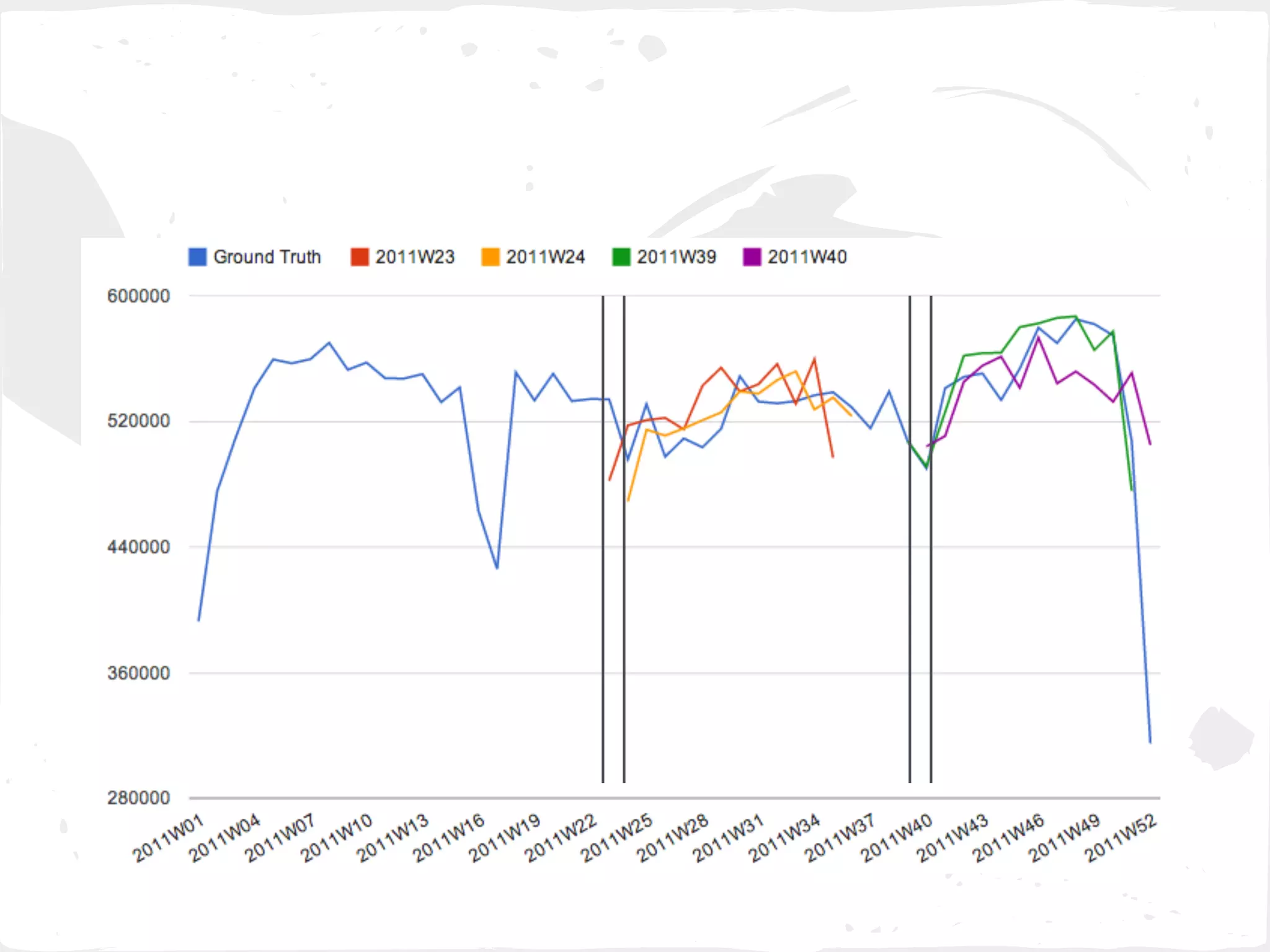
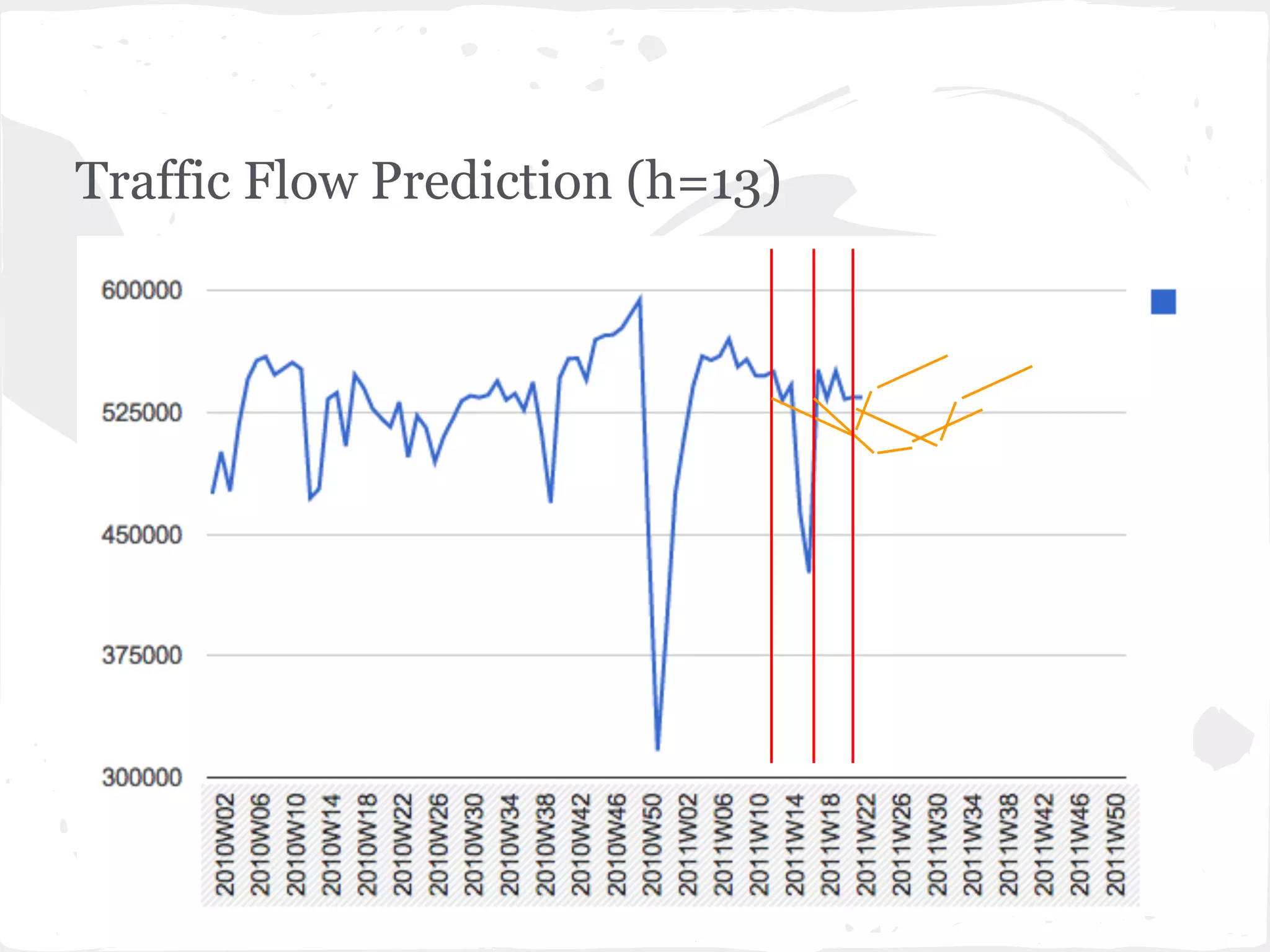
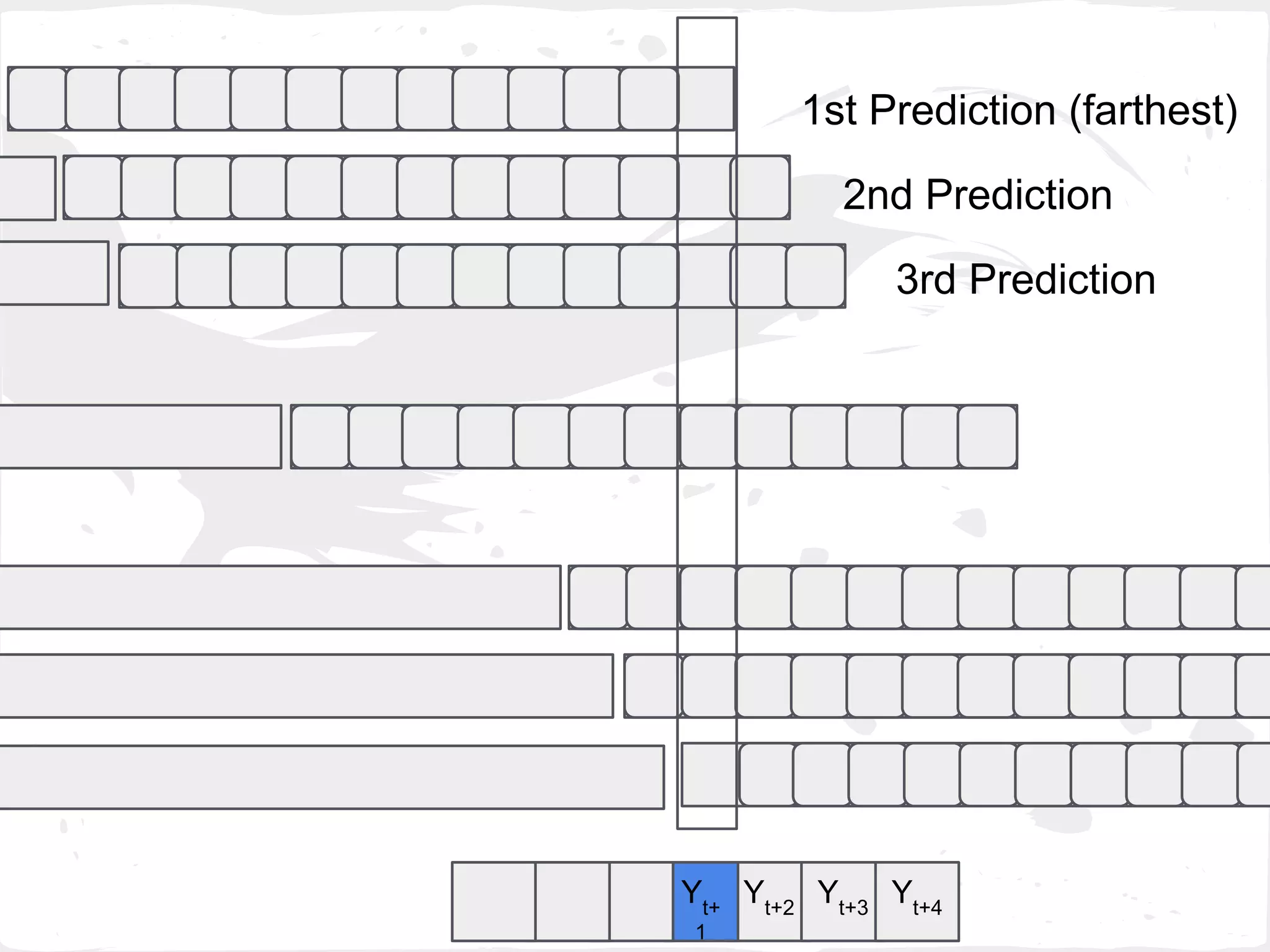
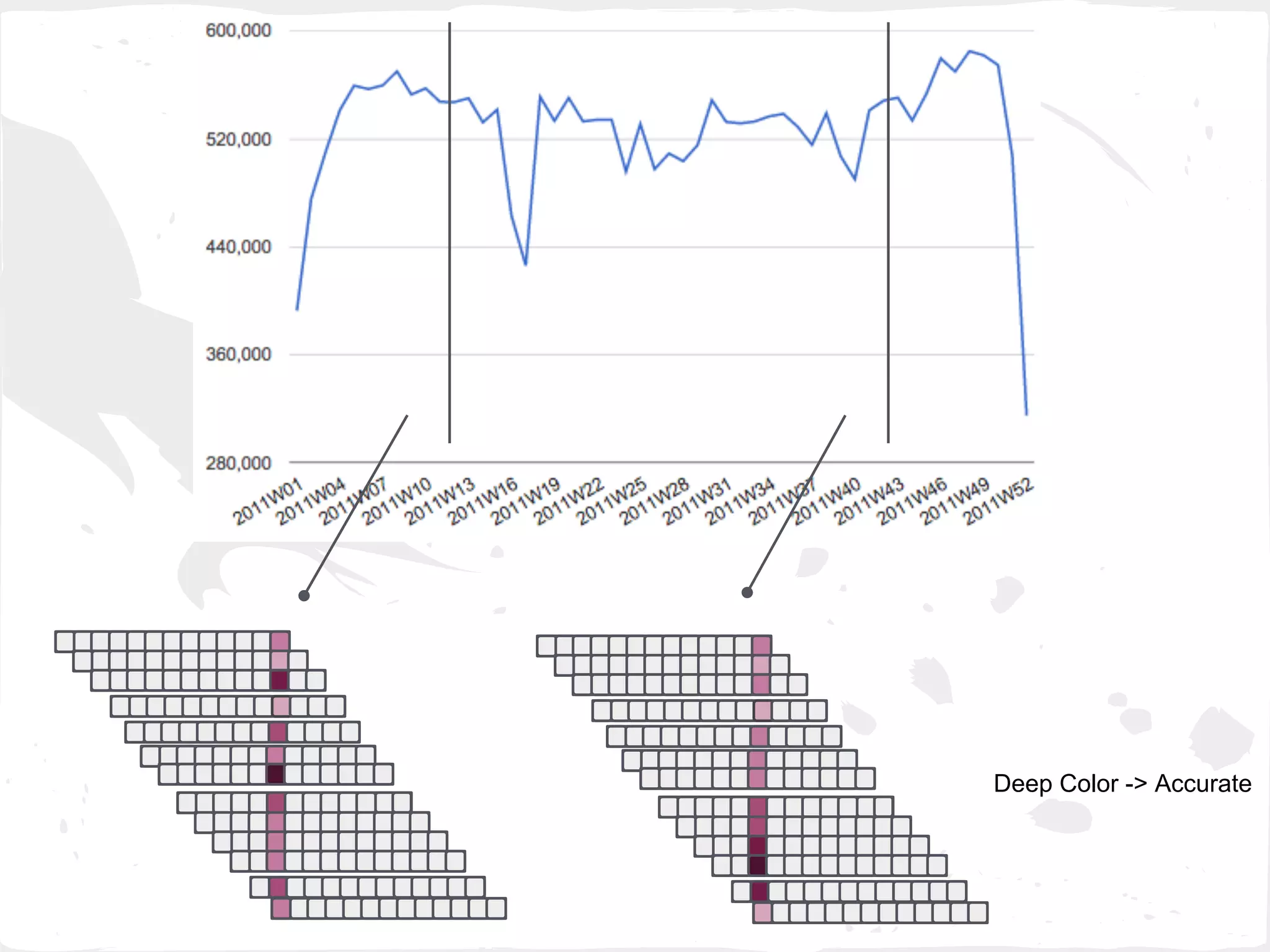
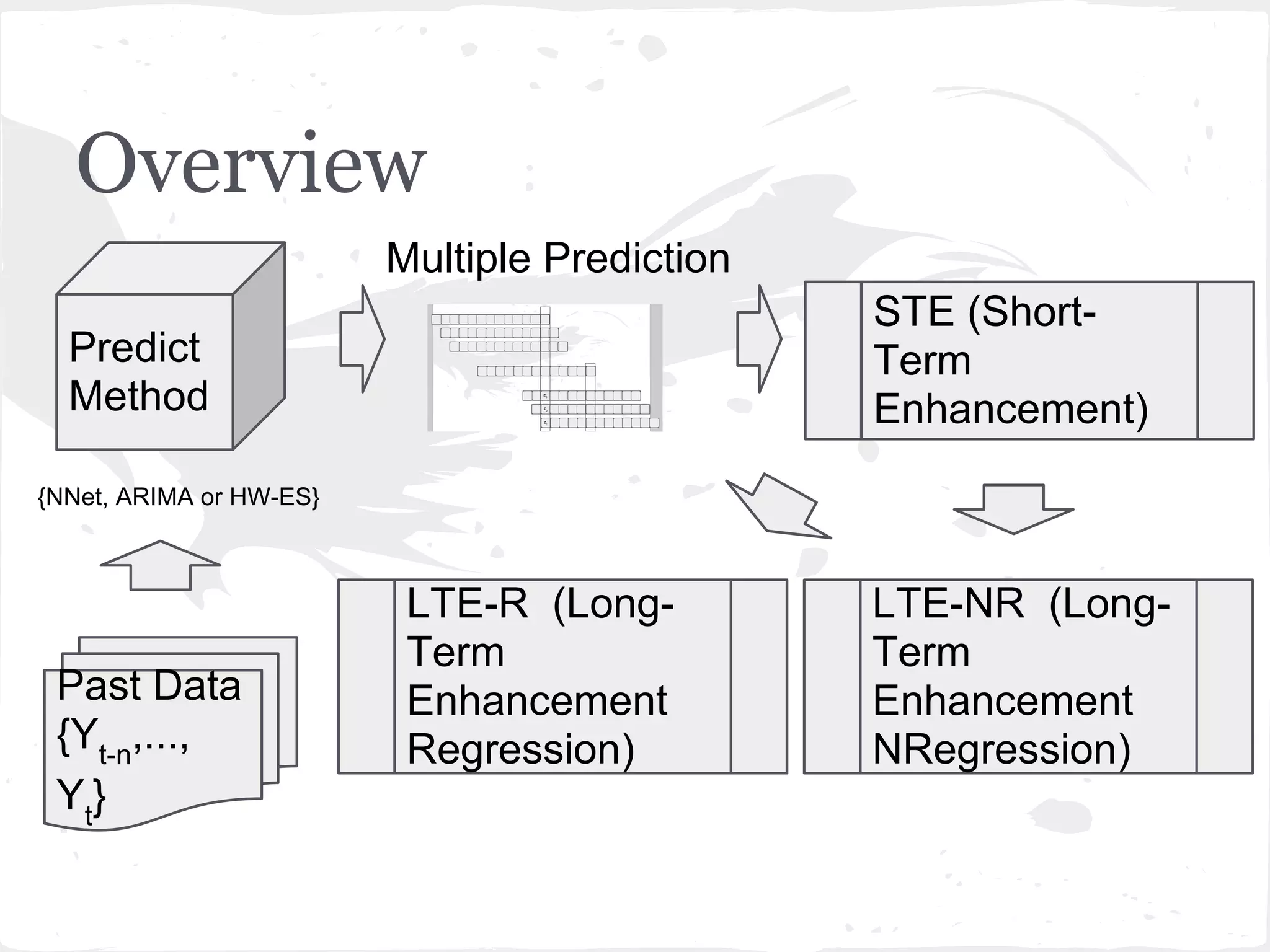
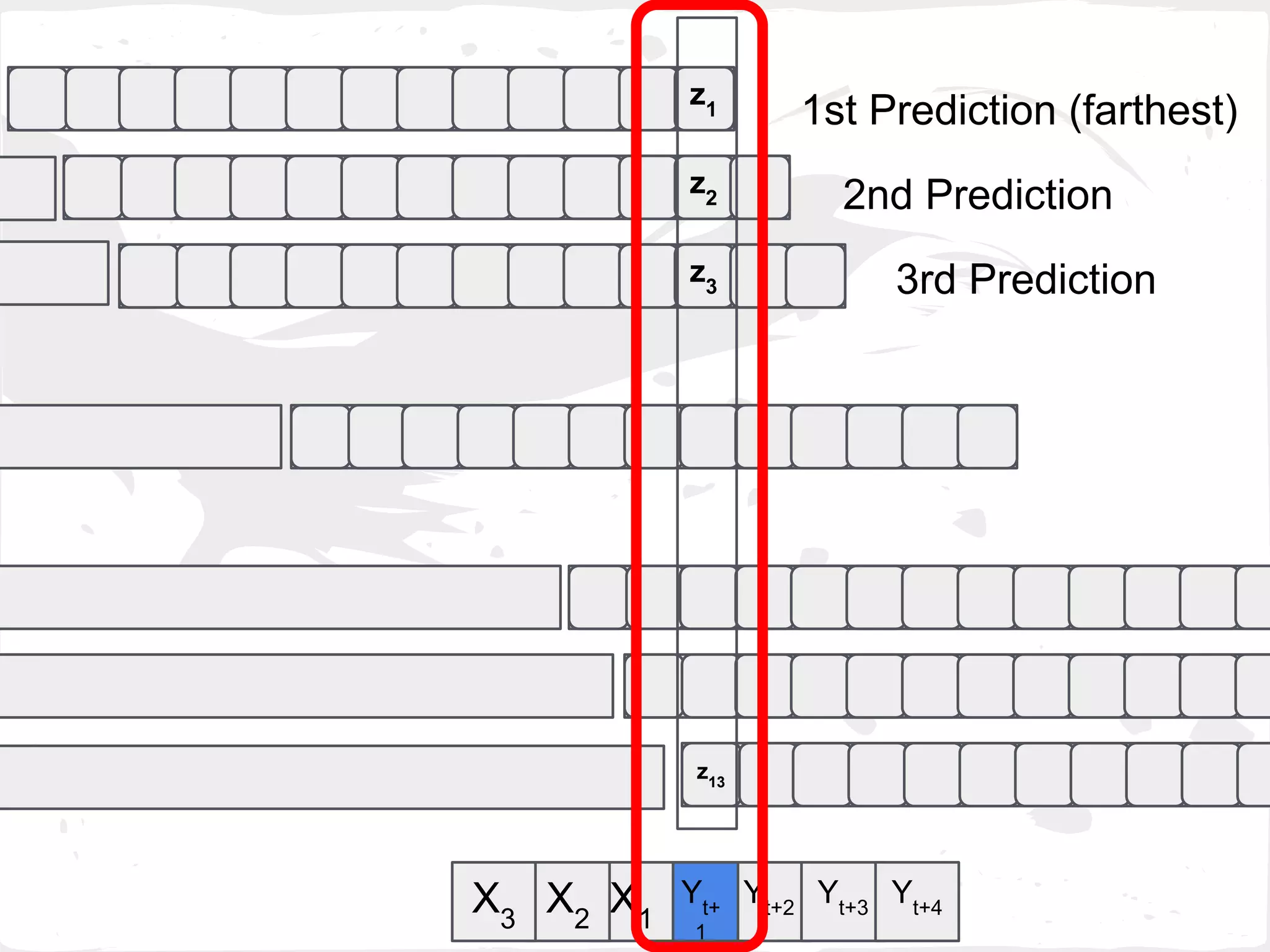
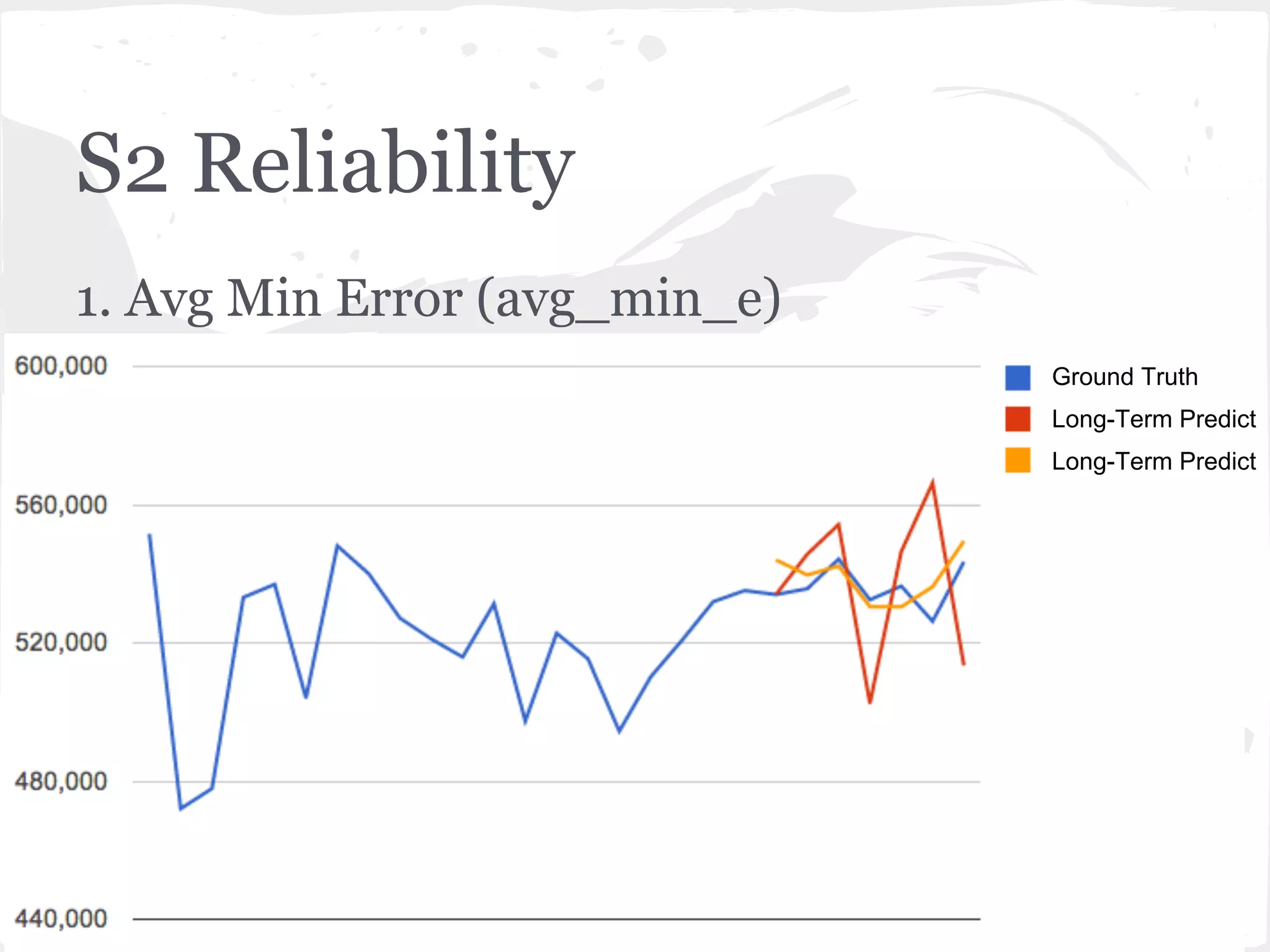
This document presents a general framework for enhancing time series prediction performance. It discusses using multiple predictions from a base method like neural networks, ARIMA or Holt-Winters to improve accuracy. Short-term enhancement uses support vector regression on statistic and reliability features of the multiple predictions to enhance 1-step ahead predictions. Long-term enhancement trains additional models on the short-term predictions to enhance longer-horizon predictions. The framework is evaluated on traffic flow data with prediction horizons of 1 week and 13 weeks.

1. A General Framework for
Enhancing Prediction
Performance on Time Series
Data
Chin-Hui Chen
陳晉暉
Prof. Pu-Jen Cheng
鄭卜壬教授
增進時序資料預測效能之一般化模型

2. 1. Motivation
2. Related Works
3. Framework
4. Experiment
5. Conclusion
Agenda

3. Motivation

4. ● Time series data is everywhere.
● For example:
○ Query Trend Data
○ Traffic Flow Data
Motivation

5. Google Trends: "typhoon". Japan, 2004 - 2013.

6. Google Trends: "typhoon". Japan, 2012.

7. Traffic Flow: ETC bridge, 2009 - 2011

8. Traffic Flow: ETC bridge, 2010

9. Predict Time Series Data
● Time series data: {Yi
} where i=1,...,t
(t = current timestamp)
Value Yi
is specific data property. E.g. Traffic
Flow, Query Frequency.
● Given {Yi
} and prediction horizon h, predict
the value of {Yj
} where j=t+1,...,t+h.

10. Predict Time Series Data
(cont'd)
● Many researches have been studying to
predict time series data. For example:
Neural Network based method, Regression
based method.
● These methods use past data {Yt-n
,..., Yt
} to
forecast future data {Yt+1
,..., Yt+h
}.
Predict
Method
Past Data
{Yt-n
,..., Yt
}
Future Data
{Yt+1
,...,
Yt+h
}

11. Predict Time Series Data
(cont'd)
● Short-term prediction
○ h=1
○ e.g. Predict {Yt+1
}.
● Long-term prediction
○ h>1
○ e.g. Predict {Yt+1
,..., Yt+13
}.

12. Traffic Flow Prediction (h=1)

13. Traffic Flow Prediction (h=13)

14. Intuitively...
● The nearer the dataset is, the more accurate
we predicts.
● The longer the prediction horizon is, the
more error occurs.

15. ● The nearer...
the dataset is, the more accurate we predicts.
● Predict Method: Exponential Smoothing
● We apply Exponential Smoothing on Traffic
Flow Data.

16. ● Traffic Flow Prediction

17. The longer...
the prediction horizon is, the more error occurs.
● Prediction Horizon = 10

18. However,
1. Trend
2. Periodicity

19. ● If the predict method captures the trend or
periodicity of the time series data, then...
● Predict Method: Neural Network
○ Capture Periodicity
nearer NOT ALWAYS accurate
longer NOT ALWAYS error

21. Also
● Continuous & Dependent
a. Time Series Data is continuous. So the prediction
can be continuous.
b. The neighbor prediction results may cover each
other and improve each other. If we want to predict
at time t, it is possible to use result at t-1 or t-2 to
cover the result.

23. Traffic Flow Prediction (h=13)

24. Multiple Prediction
● Therefore, for each data point in time series,
it has been predicted h times.
● We will have "multiple prediction" in given
data point in time series.

25. Yt+2
Yt+3
Yt+
1
Yt+4
1st Prediction (farthest)
2nd Prediction
3rd Prediction

26. Deep Color -> Accurate

27. Yt+2
Yt+3
Yt+
1
Yt+4
10/40
12/40
18/40

28. ● The most accurate result may not always
happen in the latest one.
● We propose a general enhancement
framework to utilize prediction results of
multiple prediction to improve the accuracy.

29. Related Works

30. Related Works
Time Series Predict Methods:
1. Machine Learning Based
a. Neural Network
2. Regression Based
a. ARIMA approach
b. Holt-Winters ES approach

31. Neural Network

32. NNet
The architecture of multilayer perceptron is as
follows:
● Notation: NNet(i, h)
● Input Layer: i neurons
● Single hidden layer: 4 neurons
● Output Layer: h neurons
○ The input neurons include {v(k), k = t−i+1, ..., t},
while the output neuron is {v(t+1)...v(t+h)}, where t
represents the current time.

33. ● Tangent sigmoid function and linear
transfer function are used for activation
function.
● This model is trained using back-
propagation algorithm over the training
dataset.

34. ARIMA

35. ARIMA
● Stands for "Autoregressive integrated
moving average"
● The model comprises 3 parts.
○ differencing
○ autoregressive (AR)
○ moving average (MA)
● Seasonal
○ NS-ARIMA: Nonseasonal ARIMA
○ S-ARIMA: Seasonal ARIMA

36. Differencing: non-stationary -> stationary
● stationary:
○ A stationary time series is one whose statistical
properties such as mean, variance, autocorrelation,
etc. are all constant over time.

37. NS-ARIMA
● Notation: ARIMA (p, d, q)
○ d = the order of differencing
○ p = the order of autoregressive
○ q = the order of moving average

38. NS-ARIMA
ARIMA(p, d, q):

40. S-ARIMA
ARIMA(p, d, q)(P,D,Q)s
:

41. S-ARIMA
ARIMA(p, d, q)(P,D,Q)s
:
e.g.
ARIMA(1,0,1)(1,1,2)12

42. ● In this work, S-ARIMA is adopted.

43. Holt-Winters ES

44. Holt-Winters ES
1. Stands for "Holt-Winters Exponential
Smoothing"
2.
Trend
ActualSmoothed
Periodicity

45. Framework

46. ● To improve time series prediction, a general
enhancement framework is proposed.
● The framework utilizes multiple prediction
results and tries to learn the data
dependency to improve the accuracy.

47. Predict
Method
Multiple Prediction
Overview
Past Data
{Yt-n
,...,
Yt
}
STE (Short-
Term
Enhancement)
LTE-NR (Long-
Term
Enhancement
NRegression)
{NNet, ARIMA or HW-ES}
LTE-R (Long-
Term
Enhancement
Regression)

48. ● Given a predict method, the multiple
prediction result can be generated. The
enhancement algorithms input these
information and learn from it.
● The multiple prediction result and the
corresponding labels are listed in the
following slide.

49. z13
z1
z2
z3
Yt+2
Yt+3
Yt+
1
X1
X2
Yt+4X3
1st Prediction (farthest)
2nd Prediction
3rd Prediction

50. STE (Short-Term
Enhancement)
● SVR (Support Vector Regression) is adopted.
● Target Value: Yt+1
● As the multiple prediction is done, it is
possible to have more accurate prediction
values among Z1 - Z13.

51. Feature Set
1. S1: Statistic
a. Trimmed Mean (t_mean)
b. Last N Prediction (last_n)
c. Gaussian Distribution Modeling (gaussian_dist)
2. S2: Reliability
a. Avg Min Error (avg_min_e)
b. Last Min Error (last_min_e)
c. Trend (trend)
3. Periodicity Feature

52. z13
z1
z2
z3
Yt+2
Yt+3
Yt+
1
X1
X2
Yt+4X3
1st Prediction (farthest)
2nd Prediction
3rd Prediction

53. S1 Statistic
1. Trimmed mean (t_mean)
It calculates the mean after discarding given
parts of a probability (P%) at high and low end.
Mean(Z1
,...,Zh
) trimmed with P = 10%.

54. 2. Last N Prediction (last_n)
For the elements: Zh
, Zh-1
,..., Z1
, get the lastest
N predictions. N = 1 is applied. (E.g. Z13
)

55. 3. Gaussian Distribution Modeling (gaussian_dist)
where μ = mean(Z1
,...,Zh
), σ = std(Z1
,...,Zh
)
Produce N values from the distribution. N =
1 is applied.

56. z12
z13
z1
z2
z3
Yt+2
Yt+3
Yt+
1
X1
X2
Yt+4X3
1st Prediction (farthest)
2nd Prediction
3rd Prediction
Vz1
Vz2
Vz3
Vz12

57. S2 Reliability
1. Avg Min Error (avg_min_e)
Ground Truth
Long-Term Predict
Long-Term Predict

58. 1. Avg Min Error (avg_min_e)
VZk
: the vector of partial predicted results
GTZk
: the corresponding ground truth of VZk
Select Zk
with the min MAE1
(VZk
, GTZk
)
where k = 1,...,h-1
1
MAE = Mean Absolute Error

59. 2. Last Min Error (last_min_e)
Ground Truth
Long-Term Predict
Long-Term Predict

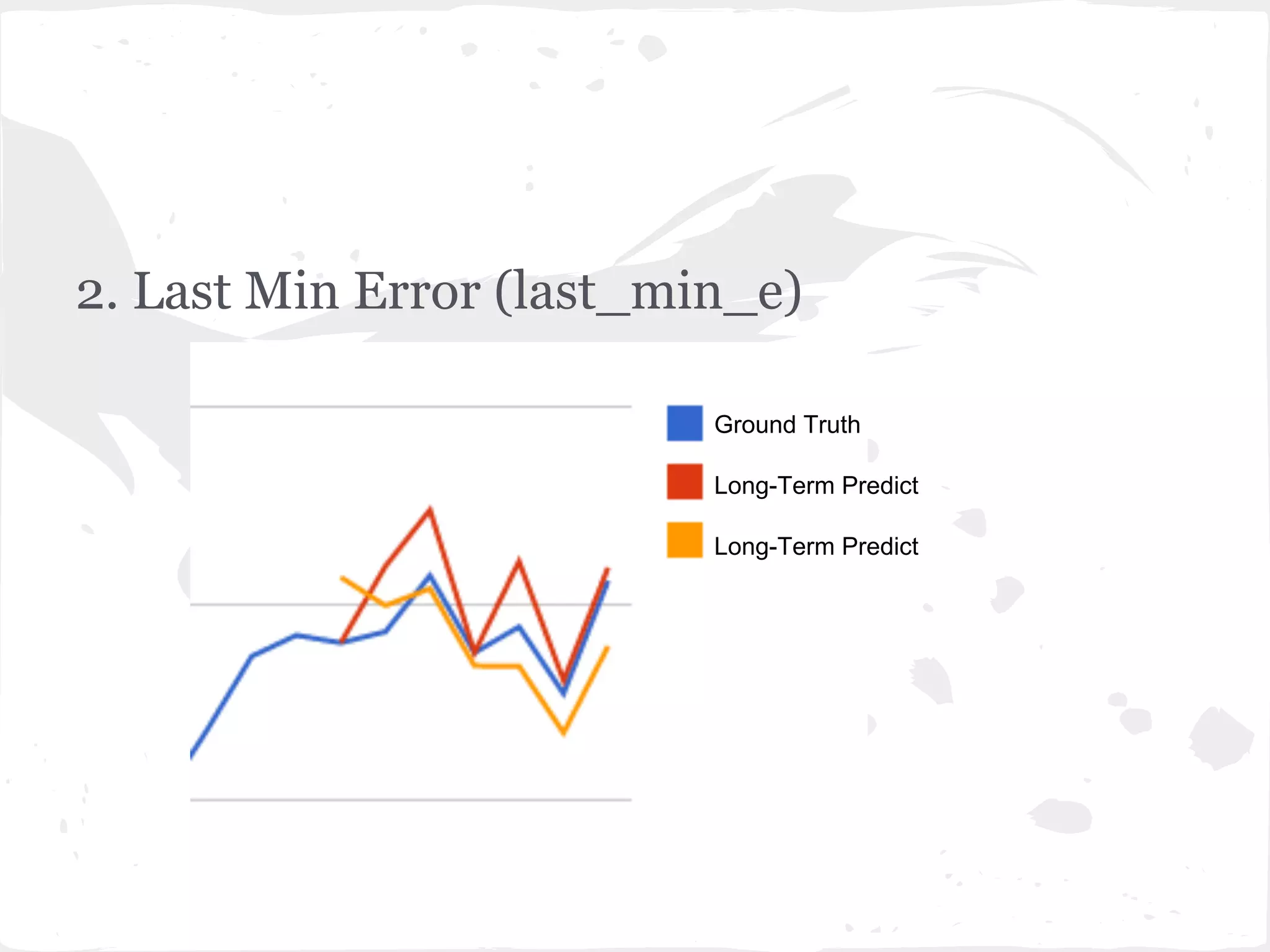
60. 2. Last Min Error (last_min_e)
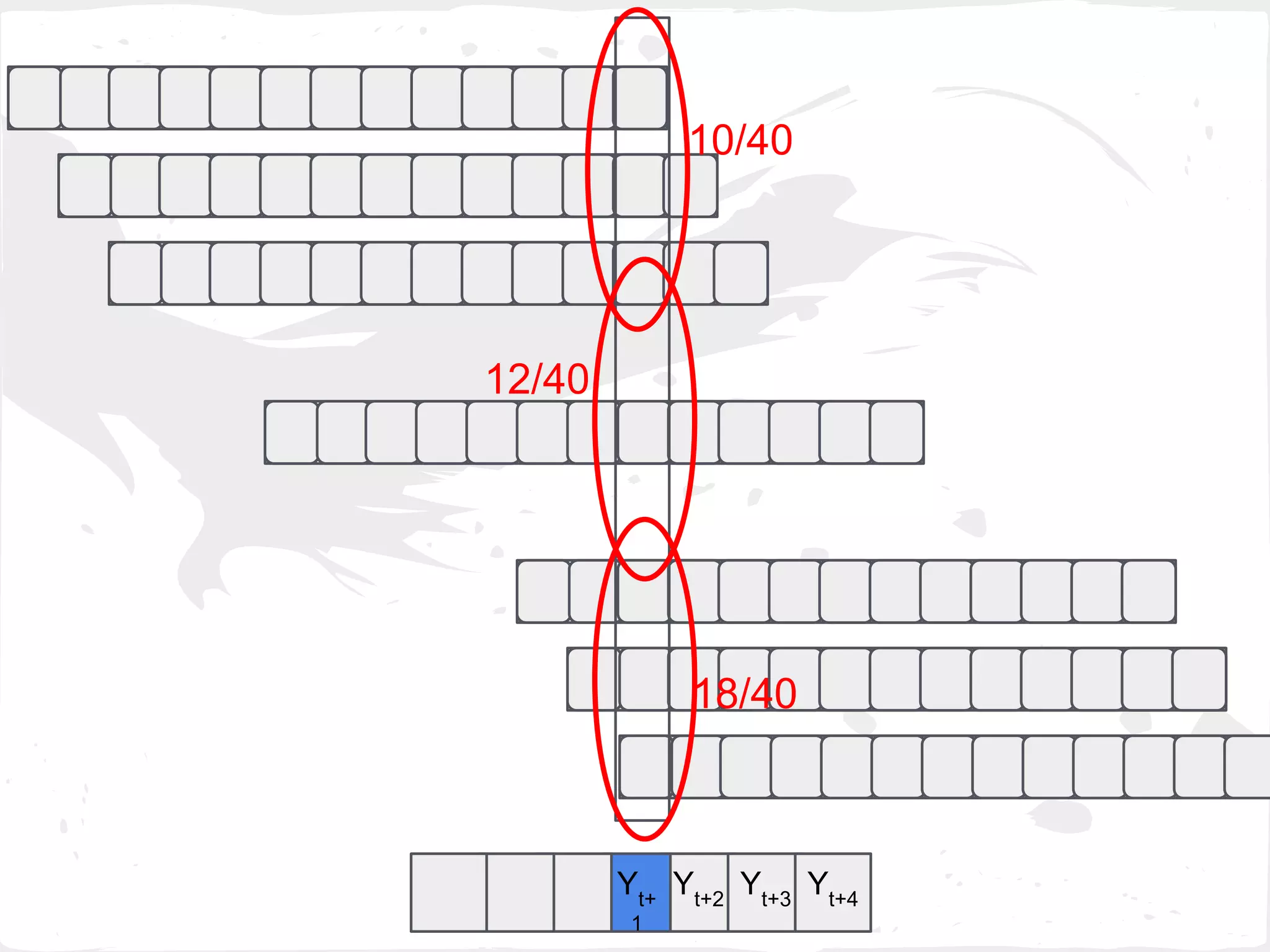
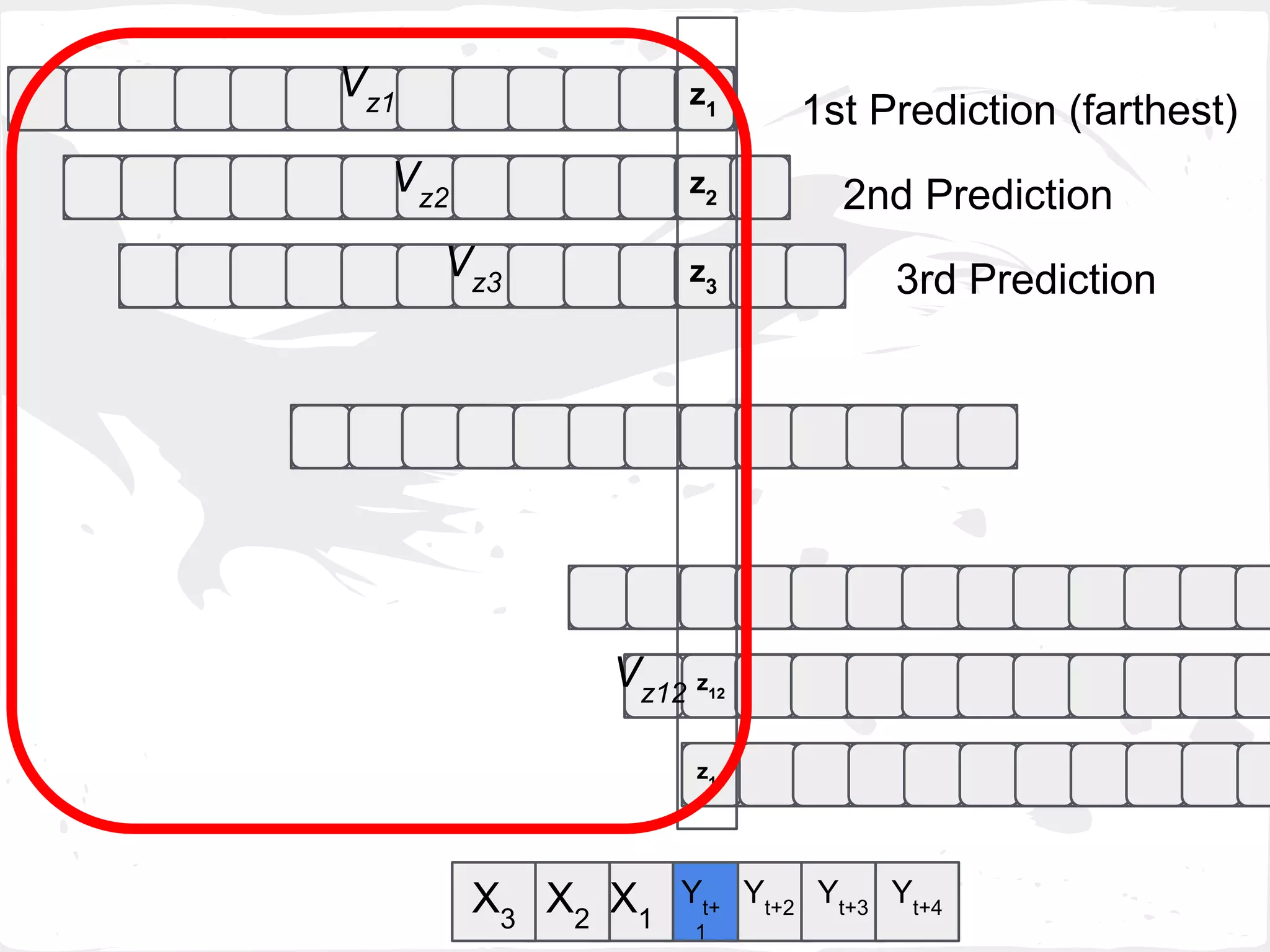
Select Zk
with the min MAE( VZk
[1] , GTZk
[1] )
where k = 1,...,h-1

61. 3. Trend (trend)
Ground Truth
Long-Term Predict
Long-Term Predict

62. 3. Trend (trend)
difference: d(m)
(t) = d(m)
(t) - d(m)
(t-1)
Select Zk
with the max
cosine_sim( d(1)
(VZk
) , d(1)
(GTZk
) )
where k = 1,...,h-1 and |VZk
|>3

63. Periodicity Feature
● The previous period data represents certain
accurate confidence. Therefore, we consider
periodicity into feature set property.
● Periodicity detection: FFT(Fast Fourier
transform)
● Add periodicity enhancement to S1 and S2.

64. Period

65. z12
z13
z1
z2
z3
Yt+2
Yt+3
Yt+
1
X1
X2
Yt+4X3
Vz1
Vz2
Vz3
Vz12
z
P
Vzp

66. Feature Set w/ Periodicity
1. S1: Statistic w/ Periodicity
a. Trimmed mean (t_mean_wp)
b. Last N Prediction (last_n)
c. Gaussian Distribution Modeling
(gaussian_dist_wp)
2. S2: Reliability w/ Periodicity
a. Avg Min Error (avg_min_e_wp)
b. Last Min Error (last_min_e_wp)
c. Trend (trend_wp)

67. S1 Statistic w/ Periodicity
1. Trimmed mean (t_mean_wp)
It calculates the mean after discarding given
parts of a probability (P%) at high and low end.
Mean(Z1
,...,Zh
,Zp
) trimmed with P = 10%.

68. 3. Gaussian Distribution Modeling
(gaussian_dist_wp)
where μ = mean(Z1
,...,Zh
,Zp
), σ = std(Z1
,...,Zh
,Zp
)
Produce N values from the distribution. N = 1 is
applied.

69. S2 Reliability w/ Periodicity
1. Avg Min Error (avg_min_e_wp)
VZk
: the vector of partial predicted results
GTZk
: the corresponding ground truth of VZk
Select Zk
with the min MAE(VZk
, GTZk
)
where k = 1,...,h-1,p

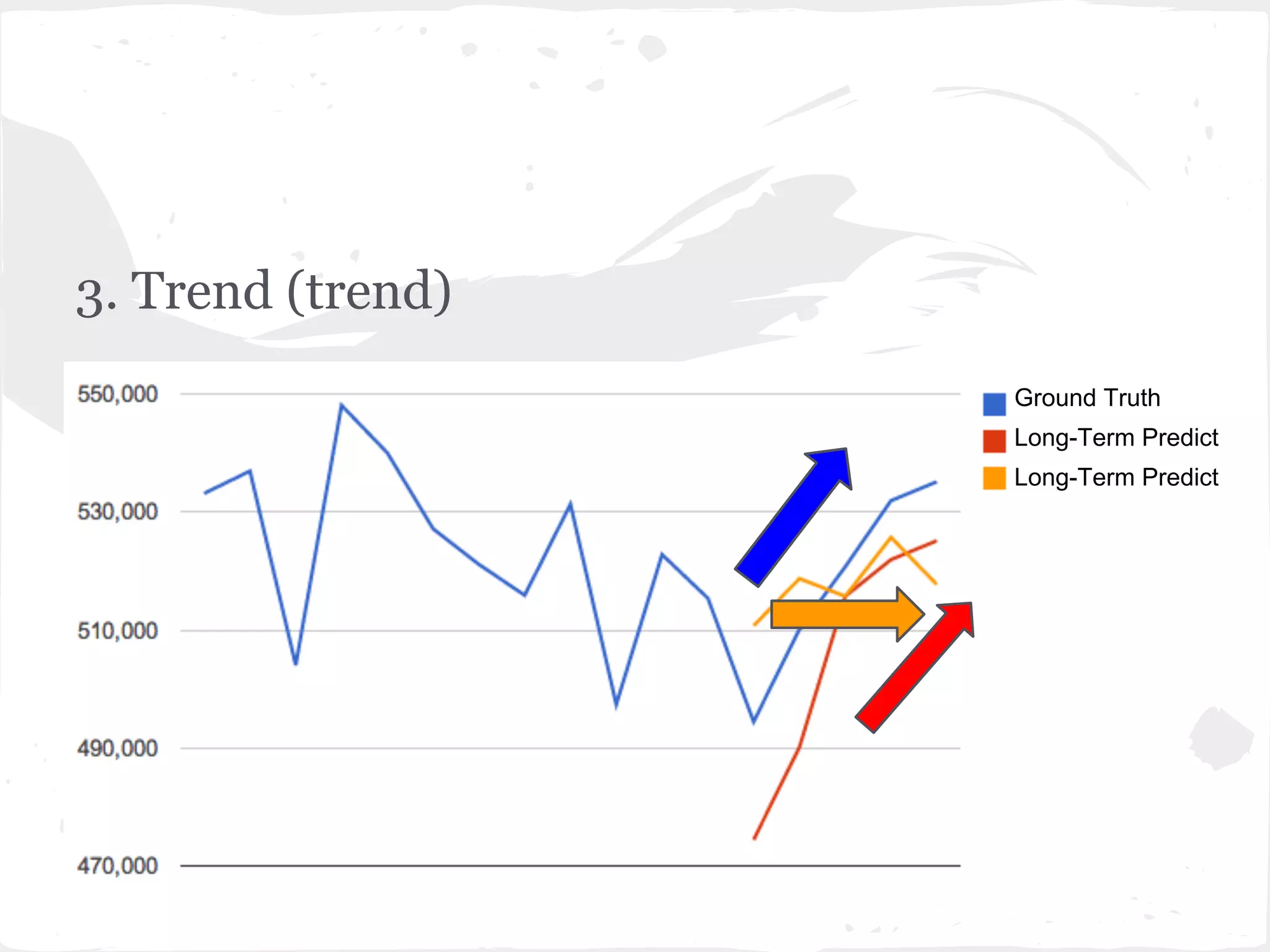
70. 2. Last Min Error (last_min_e_wp)
Select Zk
with the min MAE( VZk
[1] , GTZk
[1] )
where k = 1,...,h-1,p

71. 3. Trend (trend_wp)
difference: d(m)
(t) = d(m)
(t) - d(m)
(t-1)
Select Zk
with the max
cosine_sim( d(1)
(VZk
) , d(1)
(GTZk
) )
where k = 1,...,h-1,p and |VZk
|>3

72. Feature Set w/ Periodicity
1. S1: Statistic w/ Periodicity
a. Trimmed mean (t_mean_wp)
b. Last N Prediction (last_n)
c. Gaussian Distribution Modeling
(gaussian_dist_wp)
2. S2: Reliability w/ Periodicity
a. Avg Min Error (avg_min_e_wp)
b. Last Min Error (last_min_e_wp)
c. Trend (trend_wp)

73. z12
z13
z1
z2
z3
Yt+2
Yt+3
Yt+
1
X1
X2
Yt+4X3
Vz1
Vz2
Vz3
Vz12
z
P
Vzp

74. Predict
Method
Multiple Prediction
Overview
Past Data
{Yt-n
,...,
Yt
}
STE (Short-
Term
Enhancement)
LTE-NR (Long-
Term
Enhancement
NRegression)
{NNet, ARIMA or HW-ES}
LTE-R (Long-
Term
Enhancement
Regression)

75. LTE (Long-Term
Enhancement)
● LTE-R (Long-Term Enhancement
Regression)
● LTE-NR (Long-Term Enhancement
NRegression)

76. LTE-R (Long-Term
Enhancement Regression)
● After STE is done, the predicted result can be
used to improve Long-Term prediction.
● Given a predict method, the method takes
STE result as one of the input value and
make enhanced predictions.
●
...

77. LTE-NR (Long-Term
Enhancement NRegression)
● Train multiple SVRs to make N predictions.
Yt+2
Yt+3
Yt+
1
X1X2
Yt+4X3
Vz1
Vz2
Vz3
Vz12
Vzp

78. LTE-NR (Long-Term
Enhancement NRegression)
● These N predicted results can be passed into
the predict method to enhance the
prediction.
● LTE-R is the special case of LTE-NR when
N=1
● The behavior is illustrated.
...

79. LTE (Long-Term
Enhancement)
● LTE-R
● LTE-NR
...
...

80. Predict
Method
Multiple Prediction
Overview
Past Data
{Yt-n
,...,
Yt
}
STE (Short-
Term
Enhancement)
LTE-NR (Long-
Term
Enhancement
NRegression)
{NNet, ARIMA or HW-ES}
LTE-R (Long-
Term
Enhancement
Regression)

81. Experiment

82. Dataset
●
BRS:
ETC Data from Bridge
Roadside System in Oceania
Data Range Jan, 2009 - Dec, 2011 (3 yrs)
Time Interval Week (ISO Week Date)
Data Weekly Traffic Flow

83. ● Traffic-Flow Theory
○ Traffic stream properties: speed(v), density(k), flow
(q).
○ Flow(q)*:
i. x1
: a specific detection point.(e.g., induction loop)
ii. m: the number of vehicles passing through x1
.
iii. T: a predefined time interval. (e.g., 1 month)
* Henry Lieu (January/February 1999). "Traffic-Flow Theory". Public Roads (US Dept of
Transportation) (Vol. 62· No. 4).

84. Induction Loop
Photo via http://auto.howstuffworks.com/car-driving-safety/safety-regulatory-devices/red-light-
camera1.htm

87. Observation
1. Periodicity observed.
2. Spring and summer: Dissimilar, shifting.
3. Fall: Regular.
4. Winter: Small disturbance.

88. Experiment Setting
● Training Data: 2009, 2010 (104 weeks)
● Testing Data: 2011 (52 weeks)
● Prediction horizon:
○ Short-Term: h=1
○ Long-Term: h=13 (3 months)
● Evaluate: RMSD/RMSE (stands for Root-
Mean-Square Deviation/Error )

89. Model Parameters
● NNet:
○ 5-fold CV.
○ input neurons: 52
○ output neurons: h
● ARIMA:
○ d, p, q trained by Box-Jenkins approach
○ s = 52
● HW-ES:
○ τ = 52
● SVR:
○ 5-fold CV.
○ grid search: gamma(γ)= 2^(-3:3), cost(C)= 2^(-1:6)

90. STE
● Baseline: NNet, ARIMA, HW-ES

91. NNet ARIMA HW-ES
BL 29508.35 25121.31 16438.36
S1 29096.10 (+1.40%) 27843.35* (-10.84%) 16246.83 (+1.17%)
S1_wp 24824.02** (+15.87%) 21524.15** (+14.32%) 16333.37 (+0.64%)
S2 27661.48* (+6.25%) 26718.26* (-6.36%) 15624.02* (+4.95%)
S2_wp 25178.40* (+14.67%) 21862.60* (+12.97%) 14882.54* (+9.46%)
S1+S2 28050.20* (+5.94%) 25552.13 (-1.71%) 15924.13* (+3.13%)
Total 23593.48** (+20.04%) 21182.93* (+15.68%) 15592.74* (+5.14%)
STE: BRS
T-test with p < 0.01 (**) and p< 0.05 (*) against baseline method

92. ● NNet got the best improvement.
○ NNet (+20.04%) v.s. HW-ES (+5.14%)
● HW-ES is more accurate.
○ HW-ES (16438.36 -> 15592.74)
○ NNet (29508.35 -> 23593.48)
● Periodicity feature has great improvement.
○ NNet ( +5.94% -> +20.04% )
○ ARIMA ( -1.71% -> +15.68% )

93. Feature Analysis
● To better understand the effectiveness of
features, we analyze the correlation between
RMSE and specific feature value. (RMSE v.s.
Feature)
● Three standard measurements including
Pearson’s product-moment, Kendall’s tau
and Spearman’s rho are considered.
● The absolute values of measurements are
depicted below.

94. NNet h=13

95. ● Periodicity feature overall gets better
correlation.
● Without Periodicity
○ gaussian_dist
○ last_min_error
● With Periodicity
○ last_min_error_wp
○ trend_wp

96. LTE-R (h=13)
NNet ARIMA HW-ES
BL 24321.10 20648.60 25934.51
LTE-R 23401.23*
(+3.78%)
20562.28
(+0.41%)
23636.87*
(+8.86%)
T-test with p < 0.01 (**) and p< 0.05 (*) against baseline method

97. LTE-NR (h=13)
N=1 N=2 N=3 N=4 N=5
NNet +3.78% +1.56%
(-58%)
+5.26%
(+39%)
+0.91%
(-76%)
-0.87%
(-123%)
ARIMA +0.41% +1.21%
(+195%)
+0.92%
(+120%)
+0.12%
(-70%)
+0.13%
(-68%)
HW-ES +8.86% +9.13%
(+3%)
+9.59%
(+7.6%)
+8.45%
(-4.6%)
+3.14%
(-65%)

98. ● In LTE-R, ARIMA has the best prediction.
But HW-ES improves the most.
● In LTE-NR, we can observe that when N=3
(NNet, HW-ES)or N=2(ARIMA) , the prediction
is improved greatly.

99. Conclusion

100. ● We design a general framework for
enhancing prediction performance where the
predict method can capture trend or
periodicity property.
● We adopted Read-World traffic data. With
the great improvement,
○ City's competitiveness planning
○ Improves the budget and forecast estimation
○ Improve maintenance planning to optimize the
maintenance spending