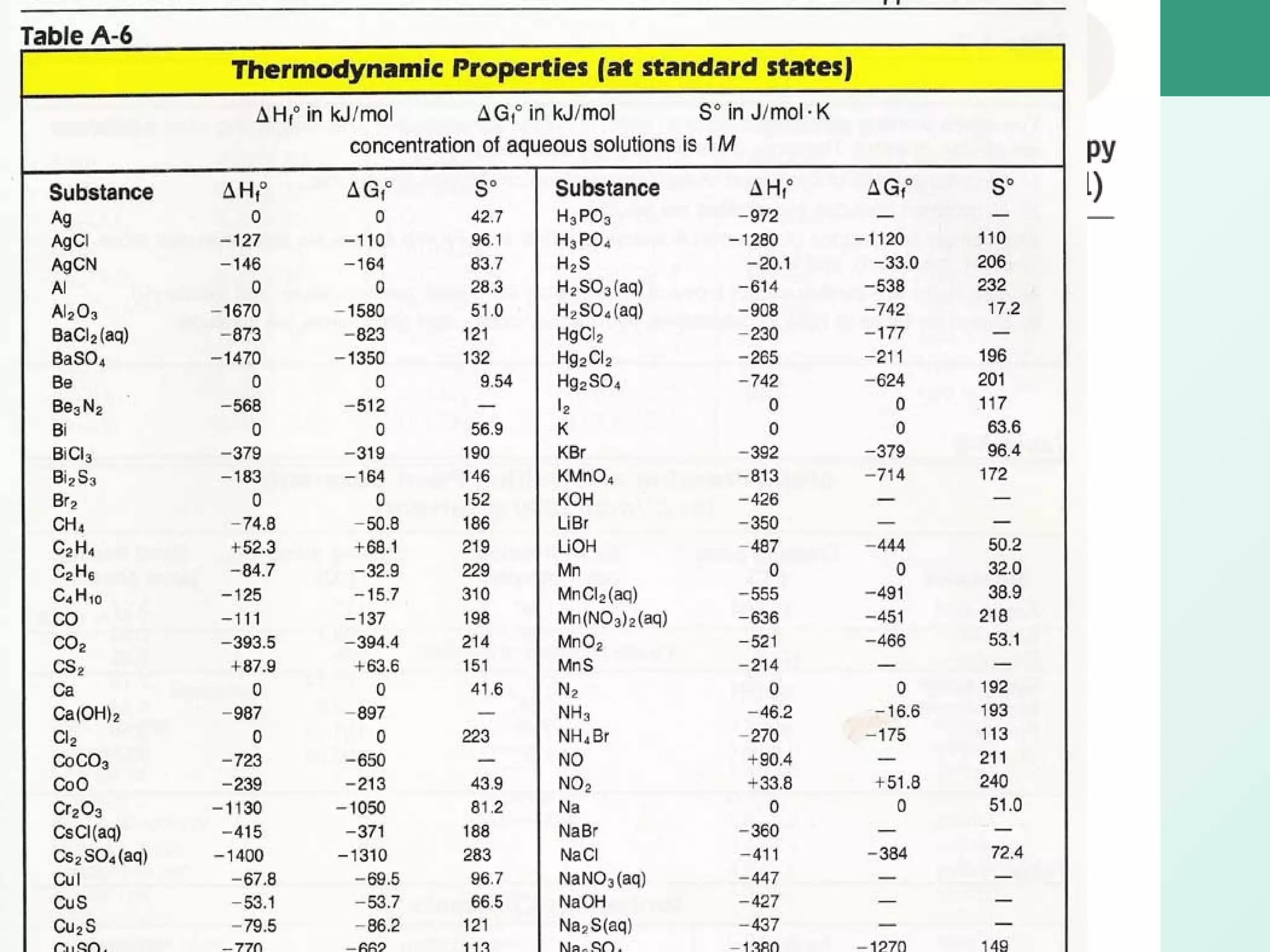
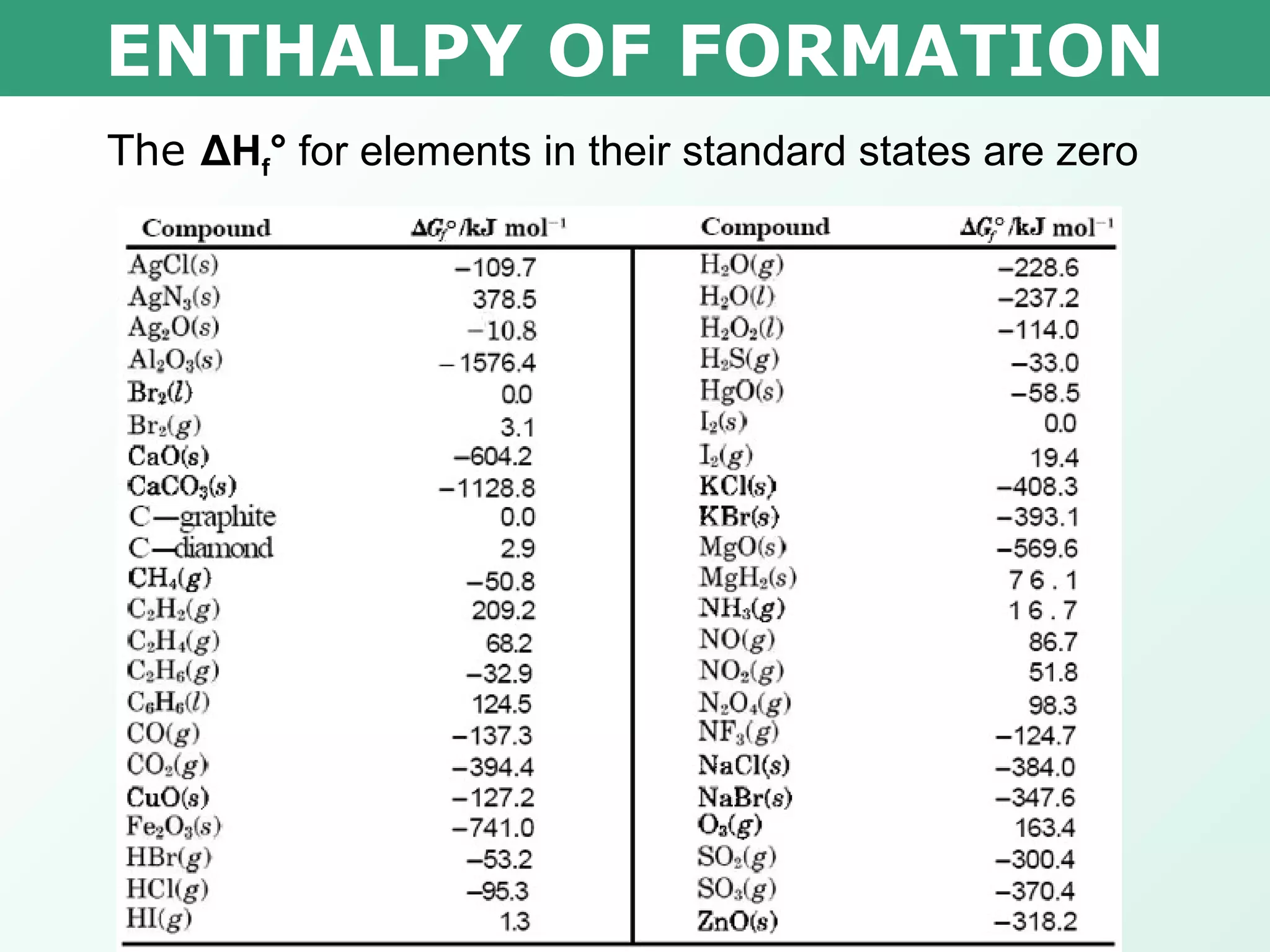
The document defines standard enthalpy of formation (ΔHf°) as the amount of heat absorbed or released when one mole of a substance is formed from its elements in their standard states at 25°C and 100kPa. ΔHf° values are used to calculate the enthalpy change (ΔH°) of a chemical reaction. Examples are provided to demonstrate how to determine the ΔHf° of a compound from combustion reactions and how to calculate ΔH° from the ΔHf° values of reactants and products.

1. ENTHALPY OF FORMATION

2. ENTHALPY OF FORMATION
Standard enthalpy of formation (ΔHf°):
Also called the standard heat of formation of
a substance
Standard heat of formation: The amount
of heat absorbed or released when one mole
of the substance is formed at 25°C and
100kPa (SATP) from its elements in their
standard states
ΔHf° units are always in kJ/mol

3. ENTHALPY OF FORMATION
Standard heat of formation: The amount of heat absorbed or
released when one mole of the substance is formed at 25°C and
100kPa (SATP) from its elements in their standard states
Example: What equation represents the formation of nitric acid?
Nitric acid = HNO3(l)
hydrogen nitrogen oxygenElements:
What are these elements in their standard (most common)
states?
½ H2(g) + ½ N2(g) + 3/2 O2(g)  HNO3(l)

4. ENTHALPY OF FORMATION
The ΔHf° for elements in their standard states are zero

5. ENTHALPY OF FORMATION
Determine the equationsfor the formation of:
a) KBrO3 K(s) + ½ Br2(l) + 3/2 O2(g)  KBrO3(s)
b) C2H5OH 2C(s) + 3H2(g) + 1/2O2(g)  C2H5OH(l)
c) NaHCO3 Na(s) + ½H2(g) + C(s) + 3/2O2(g)  NaHCO3(s)
Don’t forget that the equation must result in the
formation of one mole of the desired compound.

6. ENTHALPY OF FORMATION
Now we can assign the ΔH°f of the product as the ΔH°of
the whole reaction
2C(s) + 3H2(g) + 1/2O2(g)  C2H5OH(l) ΔH°= -235.2kJ/mol
This additional equation may assist solving Hess’ Law questions.

7. ENTHALPY OF FORMATION
How are these equations and ΔH°f
values useful?
CaO(s) + H2O(l)  Ca(OH)2(s)
By knowing the ΔH°f of each of the chemicals
in the above reaction, you can calculate the
ΔH° of the reaction without using
thermochemical equations and Hess’ Law

8. ENTHALPY OF FORMATION
∆∆H°H°ff
Formation reactions and their ΔH°f values may
be manipulated to determine balanced
equation and the ΔH°value of chemical
reactions.
ΔH°= ∑ΔH°f(products) - ∑ΔH°f(reactants)
∑ = “sum of”
Don’t forget that the equations should be
multiplied by the appropriate factor, as
necessary.

9. ENTHALPY OF FORMATION
Using ΔH°f values, calculate the ΔH° of combustion
of one mole of ethanol to produce carbon dioxide
gas and liquid water.
C2H5OH(l) + O2(g)  CO2(g) + H2O(l)3 2 3
-235.2kJ/mol 0.0000kJ/mol -393.5kJ/mol -285.8kJ/mol
ΔH° = ∑ΔH°f(products) - ∑ΔH°f(reactants)
= [(2 mol x -393.5kJ/mol) + (3 mol x -285.8kJ/mol)]
– [(1 mol x -235.2kJ/mol) + (3 mol x 0.0000kJ/mol)]
= -1644.4kJ – (-235.2kJ)
= -1409.2kJ
Since this equation already combusts 1 mole of ethanol, then the final answer is:
Therefore the heat of combustion is -1409kJ/mol of

10. ENTHALPY OF FORMATION
Using ΔH°f values, calculate the ΔH° for the following
reaction:
NaOH(s) + HCl(g)  NaCl(s) + H2O(l)
-425.6kJ/mol -92.30kJ/mol -411.2kJ/mol -285.8kJ/mol
ΔH° = ∑ΔH°f(products) - ∑ΔH°f(reactants)
= [(1 mol x –411.2kJ/mol) + (1 mol x -285.8kJ/mol)]
– [(1 mol x -425.6kJ/mol) + (1 mol x -92.30kJ/mol)]
= -697.0kJ – (-517.9kJ)
= -179.1kJ
Therefore the heat of the reaction is -179.1kJ

11. ENTHALPY OF FORMATION
Enthalpy of Combustion:
What is the reaction to produce C6H12O6?
6 CO2 + 6 H2O  6 O2 + C6H12O6
Where does this naturally occur?
How do we measure it?
In plant chloroplasts; it is not easy to
measure.

12. ENTHALPY OF FORMATION
Enthalpy of Combustion:
C6H12O6 + 6 O2  6 CO2 + 6 H2O
For complex organics, such as C6H12O6, it is
difficult to directly measure its formation.
Instead, the compound is combusted and
the products analyzed to determine ΔH°f for
the original compound.

13. ENTHALPY OF FORMATION
Enthalpy of Combustion:
∆∆H°H°cc
standard heat of combustion - the ΔH° for
the combustion of one mole of compound
Ex. CH3OH(g) + O2(g)  CO2(g) + H2O(l) ΔH°c= -727kJ

14. ENTHALPY OF FORMATION
x 0.000kJ -393.5kJ -285.8kJ
ΔH° = ∑ΔH°f(products) - ∑ΔH°f(reactants)
-1386kJ= [(2 mol x -393.5kJ/mol) + (2 mol x -285.8kJ/mol)]
– [(1 mol x x) + (3 mol x 0.000kJ/mol)]
-1386kJ= -1358.6kJ – x
x = 27.4kJ
Therefore the heat of formation is 27.4kJ/mol
Calculate the ∆H°f for C2H4.
C2H4(g) + 3 O2(g)  2 CO2(g) + 2 H2O(l) ∆H°c = -1386 kJ

15. ENTHALPY OF FORMATION
Enthalpy of Combustion:
C2H4(g) + 3 O2(g)  2 CO2(g) + 2 H2O(l) ∆H°c = -1386 kJ
Calculate the ∆H°f for C2H4.
2 CO2(g) + 2 H2O(l)  C2H4(g) + 3 O2(g) ∆H° = +1386 kJ
C(s) + O2(g)  CO2(g) ∆H° = -393.5 kJ
H2(g) + 1/2O2(g)  H2O(l) ∆H° = -285.8 kJ
2C(s) + 2H2(g)  C2H4(g) ΔHf° = ?
1
2
3

16. ENTHALPY OF FORMATION
Enthalpy of Combustion:
C2H4(g) + 3 O2(g)  2 CO2(g) + 2 H2O(l) ∆H°c = -1386 kJ
Calculate the ∆H°f for C2H4.
2 CO2(g) + 2 H2O(l)  C2H4(g) + 3 O2(g) ∆H° = +1386 kJ
x 2 2C(s) + 2O2(g)  2CO2(g) ∆H° = -787 kJ
x 2 2H2(g) + O2(g)  2H2O(l) ∆H° = -571.6 kJ
2C(s) + 2H2(g)  C2H4(g) ΔHf° = ?
1
2
3
2C(s) + 2H2(g)  C2H4(g) ΔHf° = 27.4kJ

17. ENTHALPY OF FORMATION