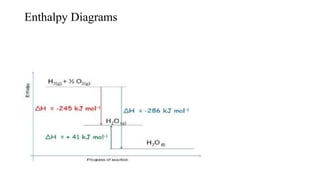
The document discusses enthalpy diagrams, which illustrate the relative internal energy of a system before and after a reaction, and how they relate to phases of matter. It explains Hess's Law, showing that the enthalpy change for an overall process can be determined by summing the enthalpy changes of individual steps, regardless of the path taken. The document also provides examples of calculating standard enthalpies of reaction and how to apply Hess's Law in chemical equations.

1. Enthalpy Diagram
Dr. K. Shahzad Baig
Memorial University of Newfoundland
(MUN)
Canada
Petrucci, et al. 2011. General Chemistry: Principles and Modern Applications. Pearson Canada Inc., Toronto, Ontario.
Tro, N.J. 2010. Principles of Chemistry. : A molecular approach. Pearson Education, Inc.

2. Enthalpy Diagrams

3. What Determines the Relative Stability of the
Solid, Liquid, and Gas Phases?
Phase
A form of matter that is uniform with respect to chemical composition and the state of
aggregation on both microscopic and macroscopic length scales.
For example,
i) liquid water
ii) ice and liquid water
Water solidifies T is lowered from 300 to 250 K at 1 atm. It vaporizes to form a gas.
When heated to 400 K at atmospheric pressure,
Dry ice (CO2), sublimes at 1 bar an normal temperature
The solid phase is the most stable state of a substance at sufficiently low temperatures, and
that the gas phase is the most stable state of a substance at sufficiently high temperatures.

4. Enthalpy Diagrams
Enthalpy diagrams are a representation of the relative internal energy of a system before
and after a reaction.
Horizontal lines are drawn to show the energy of the system at a particular time.
The formulae of all the elements or compounds present in the system including their state:
solid, liquid or gas.
A line at a higher level merely shows that the
enthalpy of the system has increased due to the
addition of heat from the surroundings, which
has caused a physical change (e.g. melting) or
chemical change (i.e. a reaction) in the system.

5. In an exothermic reaction :
Heat is evolved,
The enthalpy is decreased,
∆H is negative

6. Indirect Determination of Hess’s Law
∆H is an Extensive Property
Consider the standard enthalpy change in the formation of NO (g) from its elements at 25 oC
𝑁2 𝑔 + 𝑂2 𝑔 → 2𝑁𝑂 𝑔 ∆𝐻 𝑜 = 180.50𝑘𝐽
To express the enthalpy change in terms of one mole of we divide all coefficients
and the value by two
1
2
𝑁2 𝑔 +
1
2
𝑂2 𝑔 →
1
2
𝑥 2𝑁𝑂 𝑔 ∆𝐻 𝑜 =
1
2
𝑥 180.50𝑘𝐽 = 90.25 𝑘𝐽

7. ∆H Changes Sign When a Process is Reversed
if a process is reversed, the change in a function of state reverses sign. Thus,
∆H for the decomposition of 1 mole of NO (g) = - ∆H for the formation of 1 mole of NO (g)
𝑁𝑂 𝑔 →
1
2
𝑁2 𝑔 +
1
2
𝑂2 𝑔 ∆𝐻 𝑜 = − 90.25 𝑘𝐽
Imagine that this reaction as proceeding in two steps as given below
1
2
𝑁2 𝑔 +
1
2
𝑂2 𝑔 → 𝑁𝑂 𝑔 ∆𝐻 𝑜 = 180.50𝑘𝐽 = 90.25 𝑘𝐽

8. Imagine that the reaction as proceeding in two steps as:
1
2
𝑁2 𝑔 + 𝑂2 𝑔 → 𝑁𝑂 𝑔 +
1
2
𝑂2
∆𝐻 𝑜 = +90.25 𝑘𝐽
𝑁𝑂 𝑔 +
1
2
𝑂2 (𝑔) → 𝑁𝑂2 𝑔
∆𝐻 𝑜 = −57.07 𝑘𝐽

9. 1
2
𝑁2 𝑔 + 𝑂2 𝑔 → 𝑁𝑂 𝑔 +
1
2
𝑂2 ∆𝐻 𝑜 = +90.25 𝑘𝐽
𝑁𝑂 𝑔 +
1
2
𝑂2 (𝑔) → 𝑁𝑂2 𝑔 ∆𝐻 𝑜 = −57.07 𝑘𝐽
the overall
1
2
𝑁2 𝑔 + 𝑂2 𝑔 → 𝑁𝑂2 𝑔 ∆𝐻 𝑜 = +33. 18 𝑘𝐽

10. Hess’ s law
If a process occurs in stages or steps (even if only hypothetically),
the enthalpy change for the overall process is
the sum of the enthalpy changes for all the individual steps.
Hess s law is simply a consequence of the state function property of enthalpy.
Regardless of the path taken in going from the initial state to the final state,
∆H has the same value.

11. Applying Hess’s Law
Example 7.9
Use the heat of combustion data (given) to determine ∆H° for reaction
3𝐶 𝑔𝑟𝑎𝑝ℎ𝑖𝑡𝑒 + 4𝐻2 𝑔 → 𝐶3 𝐻8 (g) ∆H° = ?
Solution
𝑎) 𝐶3 𝐻8 𝑔 + 5 𝑂2 𝑔 → 3𝐶𝑂2 𝑔 + 4𝐻2 𝑂 𝑙 ∆H° = -2219.9 kJ
𝑏) 𝐶 𝑔𝑟𝑎𝑝ℎ𝑖𝑡𝑒 + 𝑂2 𝑔 → 𝐶𝑂2 𝑔 ∆H° = −393.5 kJ
𝑐) 𝐻2 +
1
2
𝑂2 𝑔 → 𝐻2 𝑂 𝑙 ∆H° = −285.8 kJ

12. Because our objective in reaction is to produce C3H8 (g), the next step is to find a reaction
in which C3H8 (g) is formed ---- the reverse of reaction (a)
𝑎) 𝐶3 𝐻8 𝑔 + 5 𝑂2 𝑔 → 3𝐶𝑂2 𝑔 + 4𝐻2 𝑂 𝑙 ∆H° = -2219.9 kJ
− 𝑎 : 3𝐶𝑂2 𝑔 + 4𝐻2 𝑂 𝑙 → 𝐶3 𝐻8 𝑔 + 5 𝑂2 𝑔 ∆H° = -(-2219.9) kJ = 2219.9 kJ
Now, we turn our attention to the reactants, C(graphite) and H2 (g). To get the proper
number of moles of each, we must multiply equation (b) by 3 and equation (c) by 4.
3 𝑥 𝑏): 3𝐶 𝑔𝑟𝑎𝑝ℎ𝑖𝑡𝑒 + 3𝑂2 𝑔 → 3𝐶𝑂2 𝑔
3 x ∆H° = 3 x −393.5 kJ = −1181 kJ
4 𝑥 𝑐) ∶ 4 𝑥 𝐻2 +4 𝑥
1
2
𝑂2 𝑔 → 4 𝑥 𝐻2 𝑂 𝑙 4 x ∆H° = 4 x−285.8 kJ =-1143kJ‘

13. Now, combine all the three modified equations,
Add,
Cancel out the similar available on the opposite sides of arrows,
Get, over all reaction equation
3𝐶 𝑔𝑟𝑎𝑝ℎ𝑖𝑡𝑒 + 4𝐻2 𝑔 → 𝐶3 𝐻8 𝑔 ∆H° = −104.0 kJ
In this example,
3 unrelated combustion reactions were used to determine the ‘enthalpy of
reaction’ of another reaction.

14. Standard Enthalpies of Reaction
Use Hess s law to calculate the standard enthalpy of reaction for the decomposition of
sodium bicarbonate, a minor reaction that occurs when baking soda is used in baking.
2𝑁𝑎𝐻𝐶𝑂3 𝑠 → 𝑁𝑎2 𝐶𝑂3 + 𝐻2 𝑂 𝑙 + 𝐶𝑂2 𝑔 ∆H° = ?
From Hess s law, we see that the following four equations yield the above given equation
when added together.
𝑎): 2𝑁𝑎𝐻𝐶𝑂3 𝑠 → 2𝑁𝑎 𝑠 + 𝐻2 𝑔 + 2𝐶 𝑔𝑟𝑎𝑝ℎ𝑖𝑡𝑒 + 3𝑂2 (g)
∆H° =-2 x ∆Hf° = [NaHCO3 (s)]
𝑏): 2𝑁𝑎 𝑠 + 𝐶 𝑔𝑟𝑎𝑝ℎ𝑖𝑡𝑒 +
3
2
𝑂2 𝑔 → 𝑁𝑎2 𝐶𝑂3 𝑠
∆H° = ∆Hf°[Na2CO3) (s)

15. 𝐶) ∶ 𝐻2 𝑔 +
1
2
𝑂2 𝑔 → 𝐻2 𝑂 𝑙 ∆H° = ∆Hf°[H2O] (l)
d): C(graphite) + 𝑂2 𝑔 → 𝐶𝑂2 𝑔 ∆H° = ∆Hf°[CO2] (g)
for reaction (a) is the negative of twice ∆Hf°[Na2CO3) (s).
Equations (b), (c) and (d) represent the formation of one mole each of Na2CO3 (s), CO2
(g) and H2O (l) and Thus, we can express the value of for the decomposition reaction as
∆H° = ∆Hf°[Na2CO3] (s) + ∆Hf°[H2O] (l) +∆Hf°[CO2] (g) - 2 * ∆Hf°[NaHCO3] (s)
The enthalpy change for the overall reaction is the sum of the standard
enthalpy changes of the individual steps

16. ∆𝐻 𝑜 = ∆𝐻 𝑑𝑒𝑐𝑜𝑚𝑝𝑜𝑠𝑖𝑡𝑖𝑜𝑛
𝑜
+ ∆𝐻𝑟𝑒𝑐𝑜𝑚𝑏𝑖𝑛𝑎𝑡𝑖𝑜𝑛
𝑜
∆ 𝐻 𝑑𝑒𝑐𝑜𝑚𝑝𝑜𝑠𝑖𝑡𝑖𝑜𝑛
𝑜
= ∗ 2 𝑥 ∆𝐻𝑓
𝑜
[𝑁𝑎𝐻𝐶𝑂3 𝑠 ]
∆ 𝐻𝑟𝑒𝑐𝑜𝑚𝑏𝑖𝑛𝑎𝑡𝑖𝑜𝑛
𝑜
= ∆𝐻𝑓
𝑜
𝑁𝑎2 𝐶𝑂3 𝑠 + ∆𝐻𝑓
𝑜
𝐻2 𝑂 𝑙 + ∆𝐻𝑓
𝑜
[ 𝐶𝑂2 𝑔 ]
∆𝐻 𝑜
= ∆𝐻𝑓
𝑜
𝑁𝑎2 𝐶𝑂3 𝑠 + ∆𝐻𝑓
𝑜
𝐻2 𝑂 𝑙 + ∆𝐻𝑓
𝑜
𝐶𝑂2 𝑔 − 2 𝑥 ∆𝐻𝑓
𝑜
[𝑁𝑎𝐻𝐶𝑂3 𝑠 ]
∆𝐻 𝑜
= 𝑣 𝑃 𝐻𝑓
𝑜
(𝑃𝑟𝑜𝑑𝑢𝑐𝑡𝑠) − 𝑣𝑔 ∆ 𝐻 𝑜
(𝑟𝑒𝑎𝑐𝑡𝑎𝑛𝑡𝑠) 7.21

17. Calculating from Tabulated Values of ∆Ho
Example 7.11
Let us apply equation (7.21) to calculate the standard enthalpy of combustion of ethane, a
component of natural gas
Solution
𝐶2 𝐻6 𝑔 +
7
2
𝑂2 𝑔 → 2𝐶𝑂2 𝑔 + 3 𝐻2 𝑂 𝑙
∆𝐻 𝑜 = 2 𝑚𝑜𝑙 𝐶𝑂2 𝑥∆ 𝐻𝑓
𝑜
𝐶𝑂2 𝑔 + 3 𝑚𝑜𝑙 𝐻2 𝑂 𝑥 + 3 𝑚𝑜𝑙 𝑥 ∆𝐻𝑓
𝑜
𝐻2 𝑂 𝑙
− 1𝑚𝑜𝑙 𝐶2 𝐻6 𝑥 ∆ 𝐻𝑓
𝑜
𝐶2 𝐻6 (𝑔) +
7
2
𝑚𝑜𝑙 𝑂2 𝑥 ∆𝐻𝑓
𝑜
𝑂2(𝑔)
= 2 𝑚𝑜𝑙 𝐶𝑂2 𝑥 (−393.5 𝑘𝐽/𝑚𝑜𝑙 𝐶𝑂2 𝑔 + 3 𝑚𝑜𝑙 𝐻2 𝑂 𝑥 ± 285.8 𝑘𝐽/𝑚𝑜𝑙 𝐻2 𝑂 𝑙
− 1𝑚𝑜𝑙 𝐶2 𝐻6 𝑥 − 847
𝑘𝐽
𝑚𝑜𝑙
𝐶2 𝐻6 𝑔 +
7
2
𝑚𝑜𝑙 𝑂2 𝑥 0𝑘𝐽 𝑂2(𝑔)
= −787.0 𝑘𝐽 − 857.4 𝑘𝐽 + 847 𝑘𝐽 = -1559.7 kJ

18. Calculating an Unknown Value
Use the data here and in Table 7.2 to calculate of benzene, C6H6 (l)
2𝐶2 𝐻6 𝑙 + 15 𝑂2 𝑔 → 12𝐶𝑂2 𝑔 + 6𝐻2 𝑂 𝑙 ∆𝐻0 = −6535 𝑘𝐽
Solution
2𝐶2 𝐻6 𝑙 + 15 𝑂2 𝑔 → 12𝐶𝑂2 𝑔 + 6𝐻2 𝑂 𝑙 ∆𝐻0
= −6535 𝑘𝐽
? 0 -393.5 -2858
∆𝐻 𝑜
= 𝑣 𝑃 𝐻𝑓
𝑜
(𝑃𝑟𝑜𝑑𝑢𝑐𝑡𝑠) − 𝑣𝑟 ∆ 𝐻 𝑓
𝑜
(𝑟𝑒𝑎𝑐𝑡𝑎𝑛𝑡𝑠) 7.21
∆𝐻 𝑜
= 12 𝑚𝑜𝑙 𝐶𝑂2 𝑥 −393.5
𝑘𝐽
𝑚𝑜𝑙
+ 6 𝑚𝑜𝑙 𝐻2 𝑂 𝑥 −285.5
𝑘𝐽
𝑚𝑜𝑙
− 2 𝑚𝑜𝑙 𝐶6 𝐻6 𝑥 ∆𝐻𝑓
0
𝐶6 𝐻6 𝑙 } = −6535 𝑘𝐽
∆𝐻𝑓
0
𝐶6 𝐻6 𝑙 = ? [Solve]

19. Ionic Reactions in Solutions
ions of a single type cannot be created in a chemical reaction because cations and anions
are produced simultaneously.
Therefore, a particular ion need to be chosen to which an enthalpy of formation of zero
can be assigned, in its aqueous solutions.
The ion we arbitrarily choose for our zero is H+.
Now let us see how we can use expression (7.21) and data to determine the enthalpy of
formation of OH- (aq).
𝐻+
𝑎𝑞 + 𝑂𝐻−
𝑎𝑞 → 𝐻2 𝑂 𝑙 ∆𝐻 𝑜
= −55.8 𝑘𝐽
∆𝐻 𝑜 = 𝑣 𝑃 𝐻𝑓
𝑜
(𝑃𝑟𝑜𝑑𝑢𝑐𝑡𝑠) − 𝑣𝑟 ∆ 𝐻𝑓
𝑜
(𝑟𝑒𝑎𝑐𝑡𝑎𝑛𝑡𝑠) 7.21

20. ∆ 𝐻 𝑜 = 1 𝑚𝑜𝑙 𝐻2 𝑂 𝑥 ∆𝐻𝑓
𝑜
𝐻2 𝑂 𝑙
− 1 𝑚𝑜𝑙 𝐻+
𝑥 ∆𝐻𝑓
𝑜
𝑎𝑞 ] + 1 𝑚𝑜𝑙 𝑂𝐻−
𝑥 ∆𝐻𝑓
𝑜
(𝑎𝑞)] = −55.8 𝑘𝐽
∆𝐻𝑓
𝑜
𝑂𝐻− 𝑎𝑞 =
55.8 𝑘𝐽 + (1 𝑚𝑜𝑙 𝐻2 𝑂 ∆ 𝐻𝑓
𝑜
𝐻2 𝑂 𝑙 − ( 1 𝑚𝑜𝑙 𝐻+
𝑥 ∆𝐻𝑓
𝑜
𝐻+
𝑎𝑞 )
1 𝑚𝑜𝑙 𝑂𝐻−
∆𝐻𝑓
𝑜
𝑂𝐻− 𝑎𝑞 =
55.8 𝑘𝐽 − 285.8𝑘𝐽 − 0 𝑘𝐽
1 𝑚𝑜𝑙 𝑂𝐻−
= −230.0
𝑘𝐽
𝑚𝑜𝑙
𝑂𝐻−

21. Problem Statement
Ammonia is used in the industrial preparation of nitric acid according to the equation:
4 NH3(g) + 5O2(g) → 4 NO(g) + 6 H2O(g)
What is the standard enthalpy change ∆H for this reaction?
∆𝐻 𝑜 = 𝑣 𝑃 𝐻𝑓
𝑜
(𝑃𝑟𝑜𝑑𝑢𝑐𝑡𝑠) − 𝑣𝑟 ∆ 𝐻𝑓
𝑜
(𝑟𝑒𝑎𝑐𝑡𝑎𝑛𝑡𝑠) 7.21
∆Ho = [4 × (90.3) + 6 × (-241.8)] – [4 × (-45.9) + 5 × (0)]
= -906 kJ
Solution