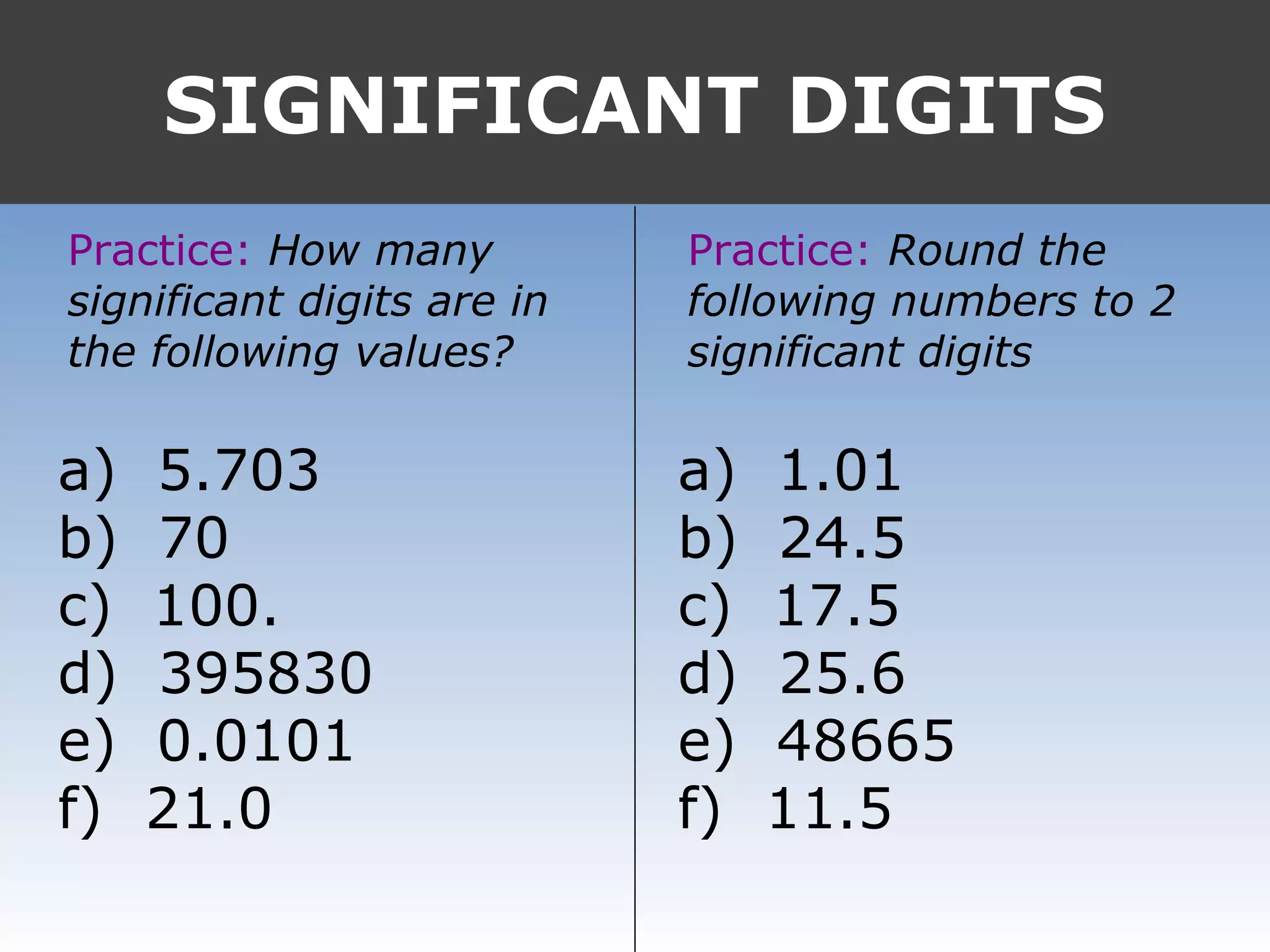
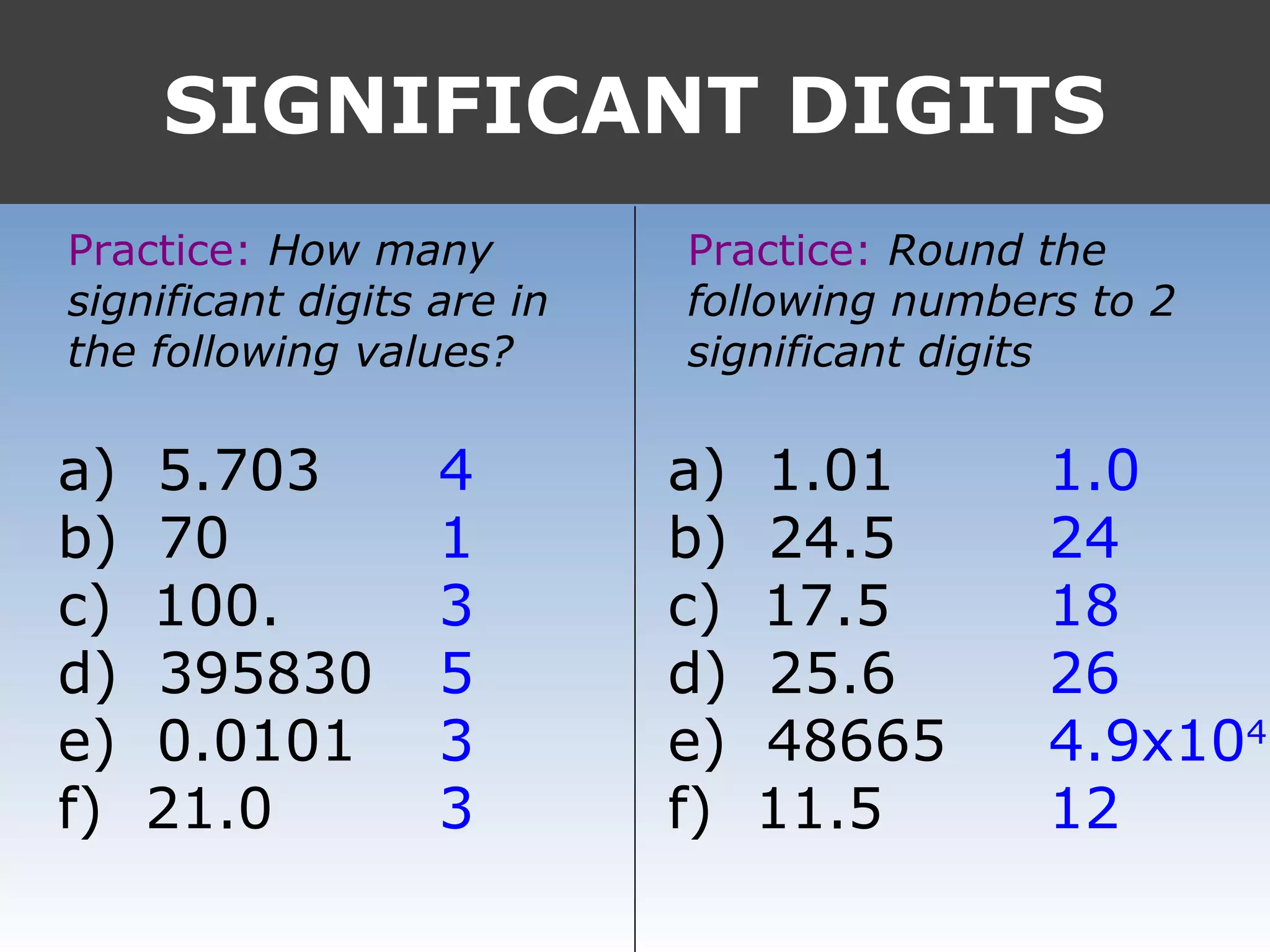
This document discusses the rules for determining significant digits in measurements and calculations. It defines four main rules: 1. All non-zero digits are significant, as are zeros between non-zero digits. 2. Leading zeros are not significant. 3. Trailing zeros may or may not be significant, depending on whether a decimal is present. 4. In calculations, the answer should match the least number of significant digits in the input values. 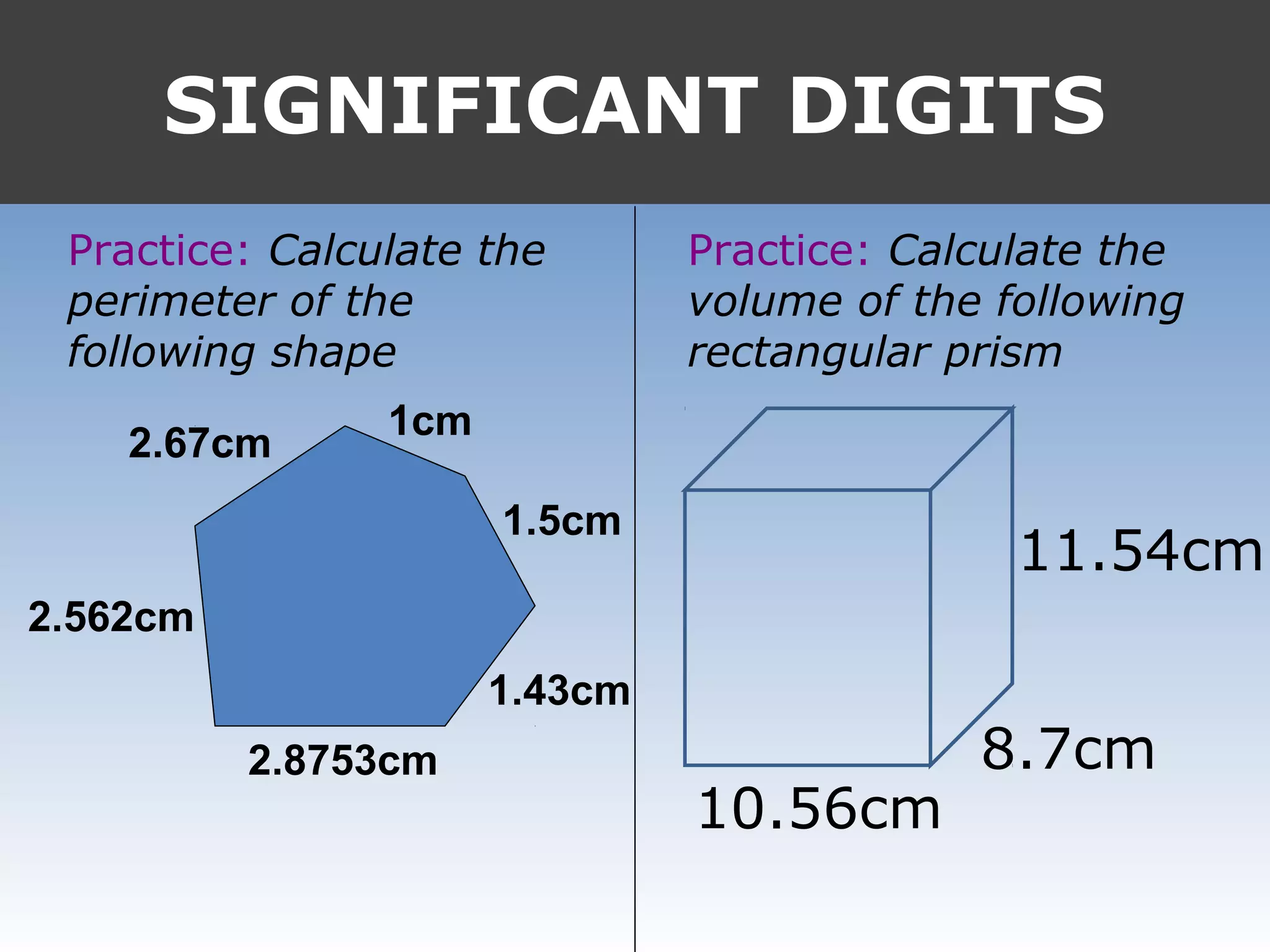It provides examples like 0.08006 having 4 significant digits, and 1000mL having 1 significant digit. The document also covers rounding rules and calculating volumes and perimeters based on measurements to the correct number of significant digits.

1. SIGNIFICANT DIGITS

2. SIGNIFICANT DIGITS
Rule #1:
All non-zero numbers are significant
Ex. 5489.213  7 significant digits

3. SIGNIFICANT DIGITS
Rule #2:
All zeros located between non-zero
numbers are significant
Ex. 0.08006  4 significant digits

4. SIGNIFICANT DIGITS
Rule #3:
Zeros located to the left of a value
are not significant
Ex. 0.00004  1 significant digit

5. SIGNIFICANT DIGITS
Rule #4:
Zeros that are located to the right of
a value may or may not be
significant
Ex. 1000.mL
4 significant digits
Ex. 1000mL
1 significant digit

6. SIGNIFICANT DIGITS
Ex. 1000mL  1 significant digit
Why?
1000mL could have been anything from
951mL to 1049mL

7. SIGNIFICANT DIGITS
Ex. 1000.0mL  5 significant digits
Why?
Rule #5
Any 0’s to the right of a decimal that
are not followed by any number are
significant

8. CALCULATIONS WITH
SIGNIFICANT DIGITS
Rule #1: Multiplying and Dividing
1.008 x 4.67
= 4.70736
= 4.71
This value has the
lowest number of
significant digits
The value with the lowest number of significant
digits determines how many significant digits
will appear in the answer

9. CALCULATIONS WITH
SIGNIFICANT DIGITS
Rule #2: Adding and Subtracting
1.008 + 4.67
= 5.678
= 5.68
This value has the
lowest number of
decimal places
The value with the lowest number of decimal
places determines how many decimal places
will appear in the answer

10. CALCULATIONS WITH
SIGNIFICANT DIGITS
Rule #3: Rounding
If greater than 5, round up
If less than 5, round down

11. CALCULATIONS WITH
SIGNIFICANT DIGITS
Rule #3: Rounding
If 5, then...
...Round up if the preceding number is
odd
Ex. 18.35
Odd
number
 18.4

12. CALCULATIONS WITH
SIGNIFICANT DIGITS
Rule #3: Rounding
If 5, then...
...Round down if the preceding number
is even
Ex. 18.25
Even
number
 18.2

13. CALCULATIONS WITH
SIGNIFICANT DIGITS
12cm
6.782cm
5.18cm
Calculate the volume of the
rectangular prism

14. CALCULATIONS WITH
SIGNIFICANT DIGITS
12cm
6.782cm
5.18cm
V= l x w x h
= (5.18cm) x (6.782cm) x (12cm)
= 421.56912cm3
= 4.2 x 102
cm3
“12” has the lowest number of significant
digits. So the answer must have 2
significant digits.

15. SIGNIFICANT DIGITS
Practice: How many
significant digits are in
the following values?
a) 5.703
b) 70
c) 100.
d) 395830
e) 0.0101
f) 21.0
Practice: Round the
following numbers to 2
significant digits
a) 1.01
b) 24.5
c) 17.5
d) 25.6
e) 48665
f) 11.5

16. SIGNIFICANT DIGITS
Practice: Calculate the
perimeter of the
following shape
Practice: Calculate the
volume of the following
rectangular prism
2.67cm
2.562cm
1cm
1.5cm
2.8753cm
1.43cm
11.54cm
8.7cm
10.56cm

17. SIGNIFICANT DIGITS
Practice: How many
significant digits are in
the following values?
a) 5.703 4
b) 70 1
c) 100. 3
d) 395830 5
e) 0.0101 3
f) 21.0 3
Practice: Round the
following numbers to 2
significant digits
a) 1.01 1.0
b) 24.5 24
c) 17.5 18
d) 25.6 26
e) 48665 4.9x104
f) 11.5 12

18. SIGNIFICANT DIGITS
Practice: Calculate the
perimeter of the
following shape
Practice: Calculate the
volume of the following
rectangular prism
2.67cm
2.562cm
1cm
1.5cm
2.8753cm
1.43cm
11.54cm
8.7cm
10.56cm
= 12.0373cm
= 12cm
= 1060.20288cm3
= 1.1x103
cm3

19. SIGNIFICANT DIGITS
Significant digits for logarithmic values:
If a solution had an H+
concentration of 2.5x10-4
mol/L,
then what is the pH to the correct number of significant
digits?
i.e. pH = - log [2.5x10-4
mol/L]
pH = 3.602059
These two digits are significant
This digit is derived from the power of 10, so it is not a significant digit
The two digits to the right of the decimal are significant
.: pH = 3.60

20. SIGNIFICANT DIGITS
What is the volume of the graduated cylinder?
What digits are you absolutely sure about?
6.6mL, 6.61mL, or
6.62mL?
6.6mL
So there are 2 significant digits in your measurement

21. SIGNIFICANT DIGITS
What is the volume of the graduated cylinder?
What digits are you absolutely sure about?
21.5mL or
21.50mL?
21.5mL
So there are 3 significant digits in your measurement

22. SIGNIFICANT DIGITS
If the scale says that your
sample is 30.69g, then
how many significant
digits are in this value?
4 significant digits
It is NOT 30.690g, because the scale is not accurate to 3 decimal places
You cannot be more accurate than what your
instrument allows.