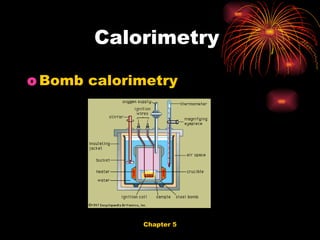
This document provides an overview of key concepts in thermochemistry, including: 1) Kinetic and potential energy, and how temperature relates to the average kinetic energy of molecules. Heat is energy transferred between objects of different temperature. 2) The first law of thermodynamics states that the change in energy of a system equals the heat added plus work done. Enthalpy (H) accounts for heat and pressure-volume work. 3) Hess's law allows determining the enthalpy change of a reaction by summing the enthalpy changes of intermediate steps. Standard enthalpies of formation (ΔH°f) quantify energy released when compounds form from elements.

1. THERMOCHEMISTRY Chapter 5

2. WARNING There is a high risk of me assuming you know or understand things that you do not. Stop me as necessary.

3. The Nature of Energy Section 5.1 is really physics Let’s look at those parts that are germane to chemistry

4. Kinetic energy E k = ½ mv 2 Kinetic energy depends on mass and velocity Temperature is a measure of the average kinetic energy of the molecules in a sample Question: why does an iceberg have more energy, then a bucket of molten iron? The Nature of Energy

5. Potential energy Usually associated with positional E p ; the rock on top of the hill In chemistry, we care more about chemical and electrostatic potential energies Chemical energies will be covered later in the chapter The Nature of Energy

6. Electrical potential energy E ep Electrical potential energy is proportional to the charges involved divided by distance We can make it equal by multiplying by a proportionality constant: E ep = k Q 1 Q 2 /d K = 8.99 x 10 9 J m/ C 2 (joule meters per coulomb squared) 1J=1Kg m 2 / s 2 The Nature of Energy

7. Calorie: a measure of heat Capitalization is IMPORTANT: 1c =4.184 J 1C = 1000c Food wrappers use C One c is the energy required to heat 1g of water one Kelvin Yes, in thermodynamics K and R must be used instead of C and F The Nature of Energy

8. Transferring energy: work & heat Work w = F orce x d istance Heat is energy transferred between objects of different temperatures (you DO NOT want to know the equations for heat transfer yet) The Nature of Energy

9. Stoichiometry is accounting for mass (atoms in must equal atoms out) Thermodynamics is accounting for energy Thermodynamics

10. System & Surroundings - The system is what we are looking at, the surroundings are the rest of the universe If work or energy are POSITIVE , work or heat go INTO the system, NEGATIVE work or heat go OUT Thermodynamics

11. `

12. Internal Energy – the sum of ALL types of energy contained in a system In thermodynamics, we look at the changes in energy, ∆E ∆ E = E final – E start If ∆E is negative, energy left the system Thermodynamics

13. The first law of thermodynamics equates energy, heat and work ∆ E = ∆q (heat) + ∆w (work) In English  the change in energy of a system is the sum of the change in heat and the work done It means “You can only get out what you put in” TANSTAAFL (There aint no such thing as a free lunch) Thermodynamics

14. ∆ E of reactions: ∆E rxn Some reactions liberate heat, others require heat to go HCl aq + NaOH aq  H 2 O+ NaCl+ HEAT This is exothermic (heat exits) HgS (s) + HEAT  Hg (l) + S 9s) This is endothermic Thermodynamics

15. State functions (and I DON’T mean dinner with Barak) State functions ONLY depend on what the state system is in NOW. I’m in front of the room. That’s a state system. It doesn’t mater how I got here, right now, I’m here. Thermodynamics

16. The distance I traveled to get here is NOT a state function. I could have went right from the door to here. I could have come in, put my stuff down on the first desk, went to the bathroom (washed my hands for 20 sec), came back, and walked to the front. Thermodynamics

17. Pressure – Volume work When a system changes volume and does work w = -P ∆V (negative since if the volume decreases, the work is done to the system Enthalpy

18. In this chapter, the pressure always stays the same , so the work done id through changing volume  w = -P ∆V It’s negative since if the piston expands, the work is done to the surroundings Enthalpy

19. Enthalpy (H) is from the Greek word enthalpein meaning to warm It equals the heat flow when P-V work is the only work done H = E + PV or ∆H = ∆ E + P ∆ V Enthalpy

20. If E = q + w , then we can put it in the enthalpy reaction as: ∆ H = ∆E – w ∆ H = ∆( q +w ) -w ∆ H = ∆q p Enthalpy

21. ∆ H is the change in enthalpy from start to final ∆H=H finish -H start In a chemical reaction, the start are the reactants and the end is the products, so: ∆ H rxn =H products -H reactants Enthalpy of Reaction

22. HCl + NH 3 -> NH 4 Cl H NH3 is -80.29; H NH4Cl is -314.4 H HCl is -92.30 ΔH = H products - H reactants ΔH products = -314.4 ΔH reactants = -92.30 + (-80.29) = -172.59 ΔH = -314.4 - 172.59 = 141.8 Enthalpy of Reaction

23. HCl + NH 3 -> NH 4 Cl + 141.8 kJ Heats of reactions and enthalpies of compounds at specified temperatures & pressures are found in tables For any class problems, they will be given to you. Enthalpy of Reaction

24. The Rules Enthalpy is EXTENSIVE it depends on the amount of material. Enthalpies are usually given in kJ/mol Enthalpy of Reaction

25. The enthalpy of a reaction is equal to the enthalpy of the reverse reaction, but the opposite sign. H 2 + F 2  2HF + 542kJ Positive means heat given off H 2 + F 2 - 542kJ  2HF 542 kJ is how much energy needed to break 2HF back to it’s components Enthalpy of Reaction

26. The enthalpy of a reaction depends on the physical state of the reactants. It takes energy to evaporate liquids and melt solids, and energy is released from condensing gases and freezing liquids. This energy MUST be accounted for. Enthalpy of Reaction

27. Enthalpy of Reaction C 6 H 12 O 6(s) + 6O 2  6CO 2(g) + 6H 2 O (l) ∆ H =-2803 Kj/mol. What if the water is a gas? ∆ H H 2 O (l)  H 2 O (g) +88 Kj/mol

28. Measurement of heat flow Requires the use of heat capacity and specific heat Heat capacity (C)– temperature change when a mass of substance absorbs a certain amount of heat (go in a sauna wearing a necklace) C is the amount of heat required to raise the object’s one kelvin Calorimetry

29. Calorimetry Specific heat is a molar quantity – the amount of heat required to one gram one Kelvin

30. How J are required to raise the temperature of 250g of Fe from 25 o C to 100 o C? 25 o C = 298K, 100 o C = 373K C s Fe= 0.45 J/gK C s = q/m∆T  0.45= q/250*75 q= 8437.5J Calorimetry

31. Works for solutions too. How J are required to raise the temperature of 250g of 2M NaCl from 25 o C to 100 o C? C s sol= 1.2 J/gK C s = q/m∆T  1.2= q/250*75 q= 22,500J Calorimetry

32. Bomb calorimetry Calorimetry

33. In a calorimeter, all the energy entering the system can be accounted for. If we subtract the energy inputs, the only other heat source is the burning sample. So the heat derived from the sample is the ∆H rxn Calorimetry

34. When a 1.000 g sample of the rocket fuel hydrazine, N 2 H 4 , is burned in a bomb calorimeter which contains 1200 g of water, the temperature rises from 24.62°C to 28.16°C. If the C for the bomb is 840 J/°C, calculate ∆ H rxn reaction for combustion of a one-gram sample ∆ H rxn for combustion of one mole of hydrazine in the bomb calorimeter Calorimetry

35. Solution For a bomb calorimeter, use this equation: ∆H rxn = -(q water + q bomb ) ∆ H rxn = -(4.18 J / g·°C x mwater x Δt + C x Δt) ∆ H rxn = -(4.18 J / g·°C x mwater + C)Δt where q is heat flow, m is mass in grams, and Δt is the temperature change. Plugging in the values given in the problem: ∆ H rxn = -(4.18 J / g·°C x 1200 g + 840 J/°C)(3.54°C) ∆ H rxn = -20,700 J or -20.7 kJ Calorimetry

36. Hess’s Law If a reaction is carried out in a series of steps, the ∆H rxn is the sum of all the intermediate ∆Hs\ The works if you can artificially separate a reaction into a number of steps. There are tables of ∆H rxn to help

37. Sometimes the tables of ∆H rxn use fractions in the chemical equation. If you have a problem using Hess’s law, you have to look at the tables and try to break your reaction into steps that are listed there. Hess’s Law

38. Use the thermochemical equations shown below to determine the enthalpy for the reaction: 2H 2 O (l) +NH 3(g) =>NO 2(g) +7/2H 2(g) 2NH 3(g) =>N 2(g) + 3H 2(g) H=138KJ 1/2N 2(g) + 2H 2 0 (l) =>NO 2(g) +2H 2(g) H=255KJ Hess’s Law

39. Hess’s Law 2H 2 O (l) +NH 3(g) =>NO 2(g) +7/2H 2(g) 2NH 3(g) =>N 2(g) + 3H 2(g) H=138KJ We only have 1 NH 3(g) , let’s divide the equation in half: NH 3(g) => ½ N 2(g) + 3/2 H 2(g) H=69KJ ½ N 2(g) + 2H 2 0 (l) =>NO2 (g) +2H 2(g) H=255KJ

40. NH 3(g) => ½ N 2(g) + 3/2 H 2(g) H=69KJ Eq. 2: ½ N 2(g) + 2H 2 0 (l) =>NO 2(g) +2H 2(g) H=255KJ Now add eq. 1 to eq. 2: NH 3(g) +½ N 2(g) + 2H 2 0 (l)  ½ N 2(g) + 3/2 H 2(g) NO 2(g) +2H 2(g) 69KJ+255Kj Hess’s Law

41. NH 3(g) + ½ N 2(g) + 2H 2 0 (l)  ½ N 2(g) + 3/2 H 2(g) NO 2(g) + 2H 2(g) 69KJ+255Kj Let’s cancel the N 2 s and add the H 2 s: 2H 2 O (l) +NH 3(g) =>NO 2(g) +7/2H 2(g) Since the two steps complete the Rxn., we add the ∆Hs Hess’s Law

42. NH 3(g) => ½ N 2(g) + 3/2 H 2(g) H=69KJ ½ N 2(g) + 2H 2 0 (l) =>NO2 (g) +2H 2(g) H=255KJ ∆ H rxn = 69KJ+ 255KJ = 324KJ Hess’s Law

43. It is a good thing to know how much energy is liberated when compounds are formed from their constituent elements This is called the enthalpy of formation ∆H f Enthalpy of Formation

44. To compare enthalpies, we need to evaluate the reactions at the same environmental conditions The is called the standard state The standard state is defined as 298K and 1 atmosphere (101.3 KPa) We denote the fact the enthalpy is measured at standard conditions with a superscript ∆H o f Enthalpy of Formation

45. Elements in their LOWEST ENERGY STATE have enthalpies of 0 The lowest energy state for oxygen is O 2 NOT O. Energy must be added (495 Kj/mol) to break the molecules, os the enthalpy is not 0 Enthalpy of Formation

46. Negative ∆H o f indicate that heat is given off during formation Positive ∆H o f indicate energy must be added during formation Compounds that require energy to be formed are those that will give off energy when decomposing (fuels) Enthalpy of Formation

47. You can use ∆H o f to determine ∆H rxn From the following heats of reaction 2 SO 2(g) + O 2(g)  2 SO 3(g) ∆ H = – 196 kJ (a) 2 S (s) + 3 O 2(g)  2 SO 3(g) ∆ H = – 790 kJ (b) calculate the heat of reaction for S (s) + O 2(g)  SO 2(g) (c) Enthalpy of Formation

48. Enthalpy of Formation Eq a 2 SO 2(g) + O 2(g)  2 SO 3(g) has the 2 SO 2(g) on the left. We can re-write the equation as the reverse reaction if we change the sign of the ∆H 2 SO 3(g)  2 SO 2(g) + O 2(g) ∆ H= +196KJ

49. (a) 2 SO 3(g)  2 SO 2(g) + O 2(g) Eq b has the SO 3 as well: (b) 2 S (s) + 3 O 2(g)  2 SO 3(g) Lets combine a & b (b first) 2 S (s) + 3 O 2(g)  2 SO 3(g) (b) 2 SO 3(g)  2 SO 2(g) + O 2(g) (a) Cancel out the 2SO 3 s and one of the O 2 s gives 2S (s) + 2O 2(g)  2SO 2(g) Enthalpy of Formation

50. 2S (s) + 2O 2(g)  2SO 2(g) Eq c was S (s) + O 2(g)  SO 2(g) So that’s HALF of –a+b. Adding those ∆H and dividing by 2: ½ (196 + – 790 kJ) = -297KJ Enthalpy of Formation

51. They are the same thing, the only difference is one goes into a gas tank, the other in a mouth. Determining the energy available from food or fuel should be easy for you now, we’ve done it for the past 20 slides. Food & Fuels