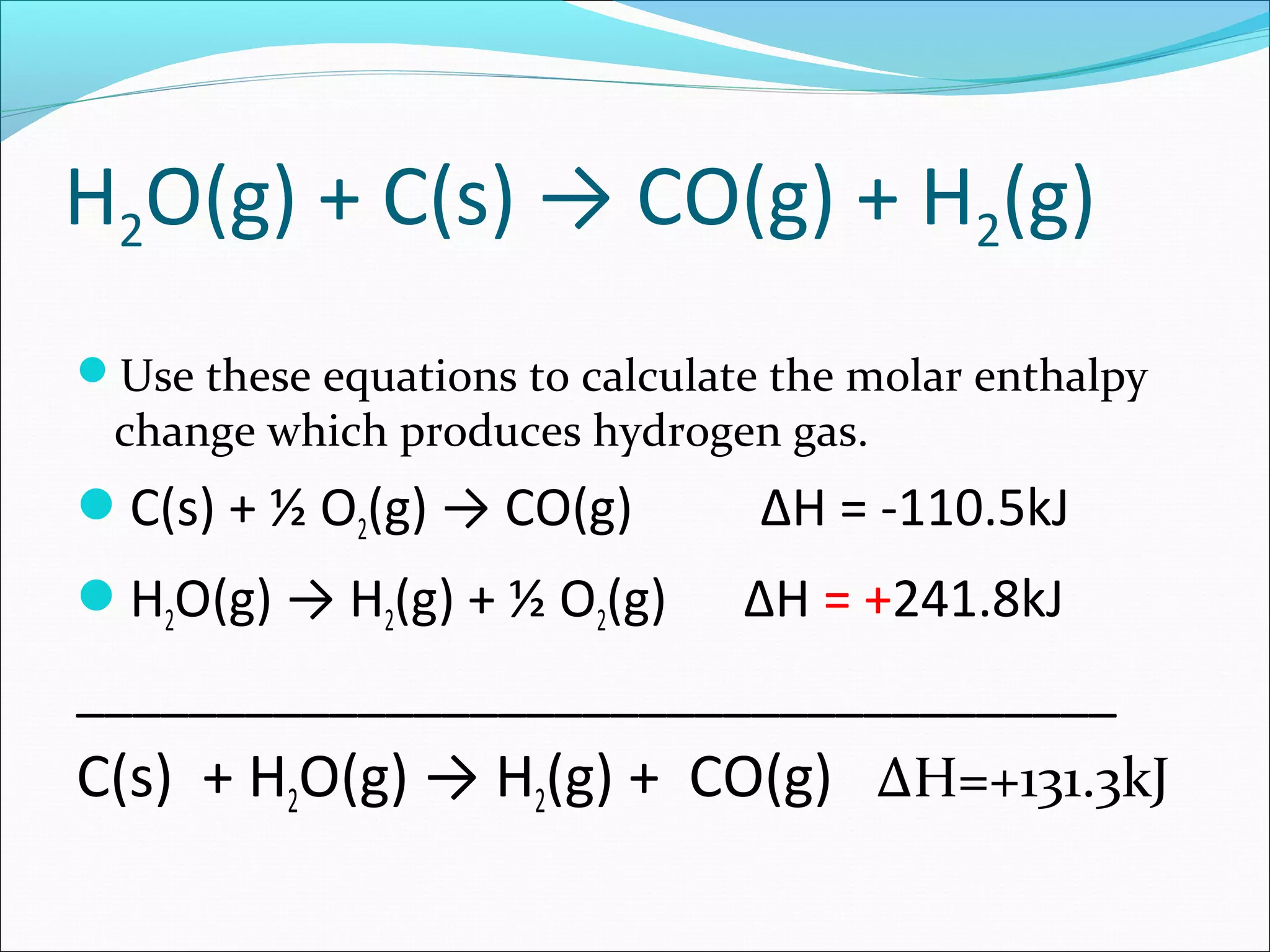The document discusses Hess's law, which states that the heat of reaction is the same whether a chemical process occurs in one or multiple steps. Specifically: - Hess's law allows adding together multiple chemical equations to determine the enthalpy change of the overall equation. - Two examples are provided to demonstrate calculating the enthalpy change of an overall reaction by combining individual reaction enthalpies. - In both examples, the individual reactions are rearranged and combined to produce the overall reaction, and the enthalpy terms are summed to find the enthalpy change of the overall reaction.

1. the heat evolved or absorbed in a chemical process is
the same whether the process takes place in one or
several steps.

2. if two or more chemical equations can be added
together to produce an overall equation, the sum of the
enthalpy equals the enthalpy change of the overall
equation.
This is called the Heat of Summation, ∆H

3. Analogy for Hess's Law
There is an old Chinese proverb
which says: There are many ways to
the top of a mountain, but the view
from the top is always the same.

4. Develop an analogy for soccer
and scoring a goal.

5. Develop an analogy for soccer
and scoring a goal.

6. Hess’s Law
Read through the whole question
Plan a Strategy
Evaluate the given equations.
Rearrange and manipulate the equations so that they
will produce the overall equation.
Add the enthalpy terms.

7. H2O(g) + C(s) → CO(g) + H2(g)
Use these equations to calculate the molar enthalpy
change which produces hydrogen gas.
C(s) + ½ O2(g) → CO(g) ∆H = -110.5kJ
H2(g) + ½ O2(g) → H2O(g) ∆H = -241.8kJ
Example 1

8. H2O(g) + C(s) → CO(g) + H2(g)
Use these equations to calculate the molar enthalpy
change which produces hydrogen gas.
C(s) + ½ O2(g) → CO(g) ∆H = -110.5kJ
H2O(g) → H2(g) + ½ O2(g) ∆H = +241.8kJ
_____________________________________
C(s) + H2O(g) → H2(g) + CO(g) ∆H=+131.3kJ

9. 4C(s) + 5H2(g) → C4H10(g)
Use these equations to calculate the molar enthalpy
change which produces butane gas.
C4H10(g) + 6 ½ O2(g) → 4CO2(g) + 5H2O(g) ∆H= -2657.4kJ/mol
C(s) + O2(g) → CO2(g) ∆H= -393.5kJ/mol
H2(g) + ½O2(g) → H2O(g) ∆H= -241.8kJ/mol
Read through the whole question
Plan a Strategy
Evaluate the given equations.
Rearrange and manipulate the equations so that they will produce the overall
equation.
Add the enthalpy terms. REWRITE THE CHANGES.
Example 2

10. 4C(s) + 5H2(g) → C4H10(g)
Use these equations to calculate the molar enthalpy
change which produces butane gas.
C4H10(g) + 6 ½ O2(g) → 4CO2(g) + 5H2O(g) ∆H= -2657.4kJ/mol
C(s) + O2(g) → CO2(g) ∆H= -393.5kJ/mol
H2(g) + ½O2(g) → H2O(g) ∆H= -241.8kJ/mol
Example 2

11. 4C(s) + 5H2(g) → C4H10(g)
Use these equations to calculate the molar enthalpy
change which produces butane gas.
5H2O(g) + 4CO2(g) → 6 ½ O2(g)+ C4H10(g) ∆H= +2657.4kJ/mol
C(s) + O2(g) → CO2(g) ∆H= -393.5kJ/mol
H2(g) + ½O2(g) → H2O(g) ∆H= -241.8kJ/mol
Example 2

12. 4C(s) + 5H2(g) → C4H10(g)
Use these equations to calculate the molar enthalpy
change which produces butane gas.
5H2O(g) + 4CO2(g) → 6 ½ O2(g)+ C4H10(g) ∆H= +2657.4kJ/mol
4(C(s) + O2(g) → CO2(g)) ∆H= 4(-393.5kJ/mol)
H2(g) + ½O2(g) → H2O(g) ∆H= -241.8kJ/mol
Example 2

13. 4C(s) + 5H2(g) → C4H10(g)
Use these equations to calculate the molar enthalpy
change which produces butane gas.
5H2O(g) + 4CO2(g) → 6 ½ O2(g)+ C4H10(g) ∆H= +2657.4kJ/mol
4C(s) + 4O2(g) → 4CO2(g) distribute the 4 ∆H= 4(-393.5kJ/mol)
H2(g) + ½O2(g) → H2O(g) ∆H= -241.8kJ/mol
Example 2

14. 4C(s) + 5H2(g) → C4H10(g)
Use these equations to calculate the molar enthalpy
change which produces butane gas.
5H2O(g) + 4CO2(g) → 6 ½ O2(g)+ C4H10(g) ∆H= +2657.4kJ/mol
4C(s) + 4O2(g) → 4CO2(g) distribute the 4 ∆H= 4(-393.5kJ/mol)
5(H2(g) + ½O2(g) → H2O(g)) distribute the 5 ∆H= 5(-241.8kJ/mol)
Example 2

15. 4C(s) + 5H2(g) → C4H10(g)
Use these equations to calculate the molar enthalpy
change which produces butane gas.
5H2O(g) + 4CO2(g) → 6 ½ O2(g)+ C4H10(g) ∆H= +2657.4kJ/mol
4C(s) + 4O2(g) → 4CO2(g) ∆H= 4(-393.5kJ/mol)
5H2(g) + 2½O2(g) → 5H2O(g) ∆H= 5(-241.8kJ/mol)
Example 2

16. 4C(s) + 5H2(g) → C4H10(g)
Use these equations to calculate the molar enthalpy
change which produces butane gas.
5H2O(g) + 4CO2(g) → 6 ½ O2(g)+ C4H10(g) ∆H= +2657.4kJ/mol
4C(s) + 4O2(g) → 4CO2(g) ∆H= 4(-393.5kJ/mol)
5H2(g) + 2½O2(g) → 5H2O(g) ∆H= 5(-241.8kJ/mol)
_____________________________________________________
∆H = -125.6kJ/mol
Example 2