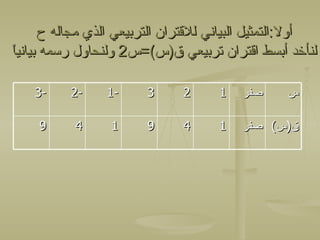
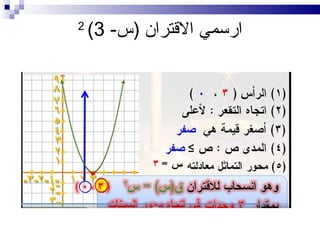
تتناول الوثيقة كيفية تمثيل وحل القترانات التربيعية، بدءًا من التعريف الأساسي للقتران تربيعي وكيفية رسمه. تشرح الوثيقة خطوات حساب قيم القتران وتقديم أمثلة على كيفية رسم المنحنى والتعريف بالرأس ومدى القتران. كما تتضمن أيضًا استخدام التمثيل البياني لحل المعادلات التربيعية.

1. ‫تمثيل القترانات التربيعية‬
‫يمكننا استخدام الرسم البياني لحل القتران‬
‫التربيعي ق)س(=أس2+ب س+ج, كما‬
‫سيتضح من المثلة اللحقة , ولكن دعنا أو ً‬
‫ل‬
‫نتعرف طريقة رسم القتران التربيعي .‬

2. ‫القتران التربيعي هو كل اقتران )س( يمكن‬
‫كتابته على الصورة:ق)س(=أس2+ب س+ج‬
‫حيث أ ب ج تنتمي ح ,أ ل تساوي صفر.‬

3. ‫ليكن ق)س(=س2+5س_6 أوجد:‬
‫ق)0(,ق)-1(,ق)1(,ق)2(,ق)-3(.‬
‫ق)0(=صفر2+خ×صفر-6=-6.‬
‫ق)-1(=)-1(2+خ×-1_6=1_5=-01.‬
‫ق)1(=)1(2+5×1_6=1+5_6=صفر.‬
‫ق)2(=)2(2+5×_6=4+01_6=8.‬
‫ق)-3(=)-3(2+5×-3_6=9+-51_6=-21‬

4. ‫إذا كان ق)س(=3_س2,أوجد:‬
‫ق)1(,ق)-1(,ق)2(,ق)0(,ق)-2(,ق)أ+1(.‬
‫ق)1(=3_)1(2=2,ق)-1(=3_)-1(2=2‬ ‫‪‬‬
‫ق)2(=3_)-2(2=_1,ق)0(=3_)0(2=3‬
‫ق)-2(=3_)-2(2=-1,ق)أ+1(=3_)أ+1(2‬

5. ‫إذا لم ُحدد المجال في السؤال يعتبر المجال‬
‫ي‬
‫جميع العداد الحقيقية ح أما مدى القتران‬
‫فهو مجموعة جميع القيم الممكنة للقتران.‬

6. ‫أول:التمثيل البياني للقتران التربيعي الذي مجاله ح‬
‫ا‬
‫لنأخد أبسط اقتران تربيعي ق)س(=س2 ولنحاول رسمه بيانيً‬
‫-3‬ ‫-2‬ ‫-1‬ ‫3‬ ‫2‬ ‫1‬ ‫صفر‬ ‫س‬
‫9‬ ‫4‬ ‫1‬ ‫9‬ ‫4‬ ‫1‬ ‫ق)س( صفر‬

8. ‫وإذا حاولنا دراسة هذا القتران بشكل أكثر فإننا نلحظ ما بأتي:‬
‫1(أصغر قيمة يأخذها القتران هي صفر وتحدث عند النقطة‬
‫)0,0(‬
‫2(القتران متماثل حول محور الصادات.‬
‫3(مدى القتران {ص:ص ≤ صفر}‬
‫4(النقطة)0,0(تسمى الرأس.‬
‫5(يسمى المنحنى المرسوم أعله قطع ً مكافئ ً.‬
‫ا‬ ‫ا‬

9. ‫إن التمثيل البياني لي اقتران تربيعي هو قطع‬
‫مكافىء.‬

10. ‫القتران ق)س(=س2+ن هو انسحاب للقتران‬
‫ق)س(=س بمقدارن‬
‫2‬
‫وحدة باتجاه محور الصادات الموجب إذا كانت‬
‫ن موجبة والسالب إذا كانت ن سالبة .‬

11. ‫3‬ ‫2+‬
‫ارسمي القتران س‬

12. ‫القتران ق)س(=)س_م(2 هو انسحاب‬
‫للقتران ق)س(=س2 بمقدار م باتجاه‬
‫محور السينات الموجب إذا كانت م موجبة‬
‫والسالب إذا كانت م السالبة.‬

13. ‫2‬
‫ارسمي القتران )س- 3(‬

14. ‫إن التمثيل للقتران ق)س(=)س-م(2 +ن هو‬
‫انسحاب للقتران ق)س(=س2 بمقدار م وحده‬
‫بإتجاه محور السينات ثم ن وحدة بإتجاه محور‬
‫الصادات وتكون احداثيات رأس القطع‬
‫المكافىء هي )م,ن(.‬

16. ‫مثال:‬

17. ‫كيف انسحب القتران:‬

18. ‫ثم:‬

19. ‫ثانيً: استخدام التمثيل البياني في حل المعادلة‬
‫ا‬
‫التربيعيه.‬

20. ‫ارسم المنحنى التقريبي للقتران‬
‫ق)س(=س2-4س+1 ثم استخدم الرسم في حل‬
‫المعادلة س2-4س+1=صفر‬
‫الحل:نحاول الكتابه س2-4س+1على صورة )س_م(2 +ن‬
‫س2_4س+1 =)س2-4س+4(+1-4‬
‫=)س-2(2+-3‬
‫=)س-2(2+-3‬
‫الرأس )2و-3( إن حل المعادلة س2-4س+1=صفر هو‬
‫الحداثي السيني لنقطة تقاطع القتران س2-4س+1مع‬
‫محور السينات ومن الرسم نلحظ أن س=٫3 0؛س=٫7 3‬