الحدوديات جدع مشترك علمي

53
أحمد الناجي أستاذ مادة الرياضيات ثانوية بئر أنزران التأهيلية
الكف اءات ا لمستهدفة
التعرف على دالة كثير حدود و على درجتها.
حل مسائل تستخدم فيها معادلات أو مت ا رجحات
من الدرجة الثانية.
  أبو بكر الكرخي )الكرجي( مثلث الكرخي لنشر n
a  b
هو أبو بكر محمد بن الحسن الكرخي . ولد في كرخ إحدى ضواحي بغداد، ولا يعرف تاريخ
ولادته ويعد أحد كبار الرياضياتيين العرب . اهتم الكرخي اهتماماً كبي ا رً بعلمي الحساب والجبر
إلا أنه لم يكن ميالاً لاستعمال الأرقام بل كان يثبت الأعداد مكتوبة بالأحرف على الطريقة اليونانية.
اعتمد في أعماله على مؤلفات الخوارزمي خاصة في الجبر ولكنه ا زد عليه في المعادلات والإكثار
من الب ا رهين سواء في الطول أو في درجات المعادلات .
أوجد الكرخي في كتابه ) البديع في الجبر والمقابلة ( طرق اً جديدة لإيجاد القيم التقريبية للأعداد
والكميات التي لا يمكن استخ ا رج جذورها واستعمل في ذلك طرقاً جبرية تدل على قوة الفكر وسعة
العقل ومعرفة تامة بعلم الجبر ، ومن أشهر كتب الكرخي كتاب ) الفخري في الجبر والمقابلة (
الذي اشتمل على نظريات جديدة لم يسبقه إليها أحد ، تدل على أصالة الكرخي في التفكير ومنها
) أن العدد الذي لو أضيف إليه مربع لكان الناتج مربعاً ولو طرح منه مربعه لكان الناتج مربع اً (
كما استنبط الكرخي قانونا جديداً لإيجاد الجذر التربيعي . وفي كتاب ) الكافي في الحساب ( أوجد
2

53
2
-1 2 3
2
3
4
5
-1
-2
0 1
1
x
y
الكرخي حلولاً متنوعة وفريدة لمعادلات الدرجة الثانية . وتوفي الكرخي في عام 0101 م.
أنشطة
نشاط أول
عدد حقيقي. x
x3  2x 1x2 1 : 1. أنشر و بسط ثم رتب العبارة
2. هل العدد 103121 أولي ؟
نشاط ثان
تمثيلها البياني في Cf  و ليكن f (x)  x2  6x  المعرفة على كما يلي: 5 f نعتبر الدالة
. O, i, j  معلم
لدينا: x 1. تحقق أن من أجل كل عدد حقيقي
  و 2 f (x)  x 1x 5
f (x)  x 3  4
التالية: x المناسبة حل في المعادلات ذات المجهول f (x) 2. باستعمال عبارة
f (x)  3  جـ( 0 f (x)  ب( 5 f (x)  ا( 0
f (x)  20  و( 0 f (x)   هـ( 4 f (x)  x  د( 1
ماذا تمثل حلول كل معادلة من المعادلات السابقة ؟
نشاط ثالث
  ذا المعادلة: 2 P المنحني  O; i , j  نعتبر في معلم
y  x 1 3
) أنظر الشكل المقابل (
1. عين شعاع الانسحاب الذي يسمح بالانتقال من القطع
P إلى المنحني y  x المكافئ ذي المعادلة 2
التالية: x 2. حل جبريا في المعادلة ذات المجهول
  2
x 1 3  0
اشرح كيف يمكن إيجاد حلول المعادلة السابقة بيانيا.
و النتائج السابقة عين في P 5. باستعمال المنحني

53
2
حلول المت ا رجحة:
  2
x 1 3<0
التالية: x 4. استنتج في حلول المت ا رجحة ذات المجهول
  2
x 1 30
تحقق جبريا .
أنشطة
نشاط ا ربع
ورد في كتاب " المختصر في حساب الجبر و المقابلة " لمحمد ابن موسى الخوارزمي ما يلي:
" ... و أما الجذور و العدد التي تعدل الأموال فنحو قولك ثلاثة أجذار و أربعة من العدد يعدل مالا فبابه أن تنصف
الأجذار فتكون واحدا و نصف فاضربها في مثلها فتكون اثنين و ربعا فزدها على الأربعة فتكون ستة و ربعا فخذ
جذرها و هو اثنان و نصف فزده على نصف الأجذار و هو واحد و نصف فتكون أربعة و هو جذر المال و المال
ستة عشر. و كل ما كان أكثر من مال أو أقل فاردده إلى مال واحد ... "
تحقق أن المعادلات المشار إليها في النص هي x و بجذر المال x 1. علما أن في النص السابق يعنى بالمال 2
" 3x  4  x و أن المثال المذكور هو: " 2 " bx  c  ax من الشكل: " 2
3 المقدم من قبل الخوارزمي – كلاميا – x  4  x 2. أكتب باستعمال الرموز حل المعادلة 2
bx  c  x 5. أعط حسب الخوارزمي في الحالة العامة صيغة الحل الموجب للمعادلات من الشكل: 2
3x  20  2x 4 و 2 x  5  x تطبيق: عين الحل الموجب لكل من المعادلتين: 2
3 استعان الخوارزمي بالشكل الهندسي الموالي. كيف أنجز ذلك x  4  x 4. لتبرير الحل المقدم كلاميا للمعادلة 2
؟
المعطيات:
مربع ABCD
AB  x
EC  3
EC منتصف القطعة F
مربع EFGH
GI  BE
نشاط خامس

53
2
 .... 2x2  x 1  0 : x نعتبر المعادلة ذات المجهول
يؤول إلى حل المعادلة  1. بين أن حل المعادلة 1
2x 1
x
 
ذا H  و القطع ال ا زئد y  2x  المستقيم ذا المعادلة 1 O, i, j  2. باستعمال ورق ميليمتري ارسم في معلم
المعادلة 1
y
x

تحقق من صحة النتائج. . 5. استنتج بيانيا حلول المعادلة
الدرس
الدوال كثي ا رت الحدود
1. الدالة كثير حدود
معرفة على بـِ: f تعريف: نسمي دالة كثير حدود ) أو كثير حدود ( كل دالة
1
1 1 0 ( ) ... n n
n n f x a x a x a x a 
     
أعداد حقيقية ثابتة. an ، ... ، a1 ، a عدد طبيعي و 0 n حيث
أمثلة:
. x هي دالة كثير حدود و بصفة خاصة الدالة المعدومة: 0  k  x k : كل دالة ثابتة 
هي كثي ا رت حدود. x x5 ، x  x  2x2  2 ، x 0,3 x2  x  الدوال: 2 
2. درجة كثير حدود
تكتب بطريقة وحيدة على الشكل: f مبرهنة و تعريف: كل دالة كثير حدود غير معدومة
1
1 1 0 ( ) ... n n
n n f x a x a x a x a 
 an  مع 0     
p معاملاته و يسمى an ، ... ، a1 ، a تسمى الأعداد 0 ، f درجة كثير الحدود n يسمى العدد الطبيعي
p الحد a x
. p الذي درجته
أمثلة:
كل دالة ثابتة:  0   x a 0 . هي كثير حدود درجته 0 a  0
. هي كثير حدود درجته 1  a  0  x ax  b : كل دالة تآلفية 
هي كثير حدود درجته 2 ) تسمى أيضا ثلاثي حدود من الدرجة الثانية(  a  0  x ax2  bx  c : كل دالة 
ملاحظة: درجة كثير الحدود المعدوم غير معيّنة.

53
2
3. تساوي كثي ري حدود
مبرهنة:
يكون كثير حدود معدوما إذا و فقط إذا كانت كل معاملاته معدومة. 
يكون كثي ا ر حدود ، غير معدومين، متساويين إذا و فقط إذا كانا من نفس الدرجة و كانت معاملات الحدود من نفس 
الدرجة متساوية.
ax3  bx2  cx  d  2x3  x  3 : x مثال: إذا كان لدينا من أجل كل عدد حقيقي
. d  و 3 c  1 ،b  0 ، a  فإن: 2
طرائق
تمرين محلول 1
هل الدوال التالية كثي ا رت حدود ؟ في حالة الإجابة بنعم حدد درجتها.
ب( f (x)  x 12x2 3 ) ا
4 2
2
2 1
( )
1
x x
g x
x
 


  جـ( 2
h(x)  sin x 3sin x  2
كثير حدود إذا أجبنا بنعم على السؤالين التاليين: f طريقة: تكون الدالة
على الشكل: 1 f (x) معرفة على ؟ 2( هل يمكن كتابة f 1( هل
1 1 0 ... n n
n n a x a x a x a 
 ؟    
حــل:
f (x)  2x3  2x2  3x 3 : x معرفة على و لدينا من أجل كل عدد حقيقي f ا( الدالة
دالة كثير حدود من الدرجة الثالثة. f إذن الدالة
x2 1  0 ، x معرفة على لأن من أجل كل عدد حقيقي g ب( الدالة
  : x لدينا من أجل كل عدد حقيقي 2
2
2
2
1
( ) 1
1
x
g x x
x

  

دالة كثير حدود من الدرجة الثانية. g إذن الدالة
على الشكل: 1 h(x) ليست دالة كثير حدود لأنه لا يمكن كتابة h جـ( الدالة
1 1 0 ... n n
n n a x a x a x a 
    
f (x)  x3  x2  4x  دالة كثير حدود معرفة بـِ: 4 f
: x بحيث يكون من أجل كل عدد حقيقي c و b ، a 1. عين الأعداد الحقيقية

40
2
   2 f (x)  x 1 ax bx  c
f (x)  0 : x 2. حل في المعادلة ذات المجهول
حــل:
  .1 2 3 2 2 3 2 (x 1)(ax bx  c)  ax bx  cx  ax bx c)  ax  (a b)x  b c x c
ax3  (a b)x2  b cx c  x3  x2  4x  4 : x إذن من أجل كل عدد حقيقي
وهذا يعني
1
1
4
4
a
a b
b c
c
 

  
   
  
أي:
1
0
4
a
b
c
 
 
   
f (x)  x 1x2  4 : x ومنه من أجل كل عدد حقيقي
ومنه x2  أو 4 x   أي: 1 x2  4  أو 0 x 1 أي 0  x 1x2  4  يعني 0 f (x)  0 .2
S    2,1,2  : 2- ، و 2 إذن مجموعة الحلول هي ، - الحلول هي 1
الدرس
عمليات على كثي ا رت الحدود
1. عمليات على كثي ا رت الحدود
تسمح ق واعد الحساب الجبري من التوصل إلى النتائج التالية:
نتائج:
1. مجموع، فرق و جداء كثيرات حدود هي كثيرات حدود.
2. مركب كثيري حدود هو كثير حدود.
. n  p على الترتيب هو كثير حدود درجته p و n 5. جداء كثيري حدود غير معدومين درجتاهما
ليس كثير حدود و تسمى الدالة: g على كثير حدود f ملاحظة: بصفة عامة حاصل قسمة كثير حدود
( )
:
( )
f x
h x
g x
دالة ناطقة.
2. جذر كثير حدود
عدد حقيقي.  كثير حدود درجته أكبر من أو تساوي 1 و f تعريف: ليكن
. f ( )  يعني 0 f جذر لكثير الحدود  العدد
مثال:
f (x)  x3  x2  x  كثير الحدود المعرف بـِ: 2 f ليكن

41
2
 f (0)  2  f (0)  بينما العدد 0 ليس جذ ا ر له لأن 0 f ومنه 2 هو جذر لكثير الحدود f (2)  لدينا: 0
 x   3. تحليل كثير حدود باستعمال العامل
عدد حقيقي.  كثير حدود درجته أكبر من أو تساوي 1 و f مبرهنة: ليكن
لدينا: x بحيث من أجل كل عدد حقيقي g فإنه يوجد كثير حدود ) f جذر لكثير الحدود  ( f ( )  إذا كان 0
f (x)  (x  ) g(x)
مثال:
f (x)  x3 6x2 11x  كثير الحدود المعرف بـِ: 6 f ليكن
f (3)  و 0 f (2)  و 0 f (1)  لدينا 0
. f 2 و 5 هي جذور لكثير الحدود ، و منه الأعداد 1
و لدينا: f يمكن إذن تحليل
f (x)   x 1 x  2 x 3
طرائق
g(x)  3x2  x  و 1 f (x)  2x  المعرفتين بـِ: 1 g و f نعتبر الدالتين كثيري الحدود
. g f 2 و f  3 g ، f  g : 1. عين كثيرات الحدود التالية
محددا درجته. f  g 2. عين كثير الحدود
حــل:
1. بتطبيق قواعد الحساب الجبري نحصل على:
    2 f  g x  f (x)  g(x)  3x 3x
    2 2 f 3g x  2 f (x) 3g(x)  9x  x 5
      2 g f x  g f (x)  12x 10x 3
   .2 3 2 . هي 5 f  g و لدينا درجة f  g x  f (x) g(x)  6x  x  x 1
f (x)  x3  x2  4x  دالة كثير حدود معرفة بـِ: 4 f
f تحقق أن العدد 2 جذر لكثير الحدود

42
-
-
-
2
f (x)   x  2 g(x) : x بحيث يكون من أجل كل عدد حقيقي g عين كثير حدود
حــل:
بحيث من أجل كل g إذن حسب المبرهنة يوجد كثير حدود . f و منه العدد 2 جذر لكثير الحدود f (2)  لدينا: 0
f (x)  (x  2) g(x) : لدينا x عدد حقيقي
باستعمال تساوي c و b ، a ثم تعيين المعاملات g(x)  ax2  bx  c يمكن فرض g(x) طريقة: لتعيين
كما يمكن استعمال خوارزمية القسمة. (x  2) g(x) كثيري حدود و ذلك بعد نشر و تبسيط و ترتيب العبارة
g(x) : الطريقة العملية لتعيين
x2 3 2 x  x  4x  4
x3  2x2 x2  x  2 g(x)  x2  x  نجد هكذا: 2
x2  4x  4 f (x)  x  2x2  x  2 : و منه
2 x  2x
2x  4
2x  4
0
الدرس
المعادلات من الدرجة الثانية
1. المعادلة من الدرجة الثانية
ax2  bx  c  كل معادلة يمكن كتابتها على الشكل: 0 ، x تعريف: نسمي معادلة من الدرجة الثانية، ذات المجهول
. a  أعداد حقيقية ثابتة مع 0 c و b ، a حيث
a  0 ax2  bx  c : 2. الشكل النموذجي لثلاثي الحدود
2 2 b c : لدينا x من أجل كل عدد حقيقي
ax bx c a x x
a a
 
      
 
و بما أن
2 2
2
2 2 4
b b b
x x x
a a a
 
     
 
فإن
2 2
2
2 2 4
b b b
x x x
a a a
 
     
 

45
2
ومنه
2 2 2 2
2
2 2
4
2 4 2 4
b b c b b ac
ax bx c a x a x
a a a a a
      
              
     
نجد   b2  4ac بوضع
2
2
2 2 4
b
ax bx c a x
a a
   
       
  
a  0 ثلاثي حدود من الدرجة الثانية ax2  bx  c تعاريف: ليكن
 و نرمز إليه بالرمز ax2  bx  c مميز ثلاثي الحدود b2  4ac يسمى العدد 
يسمى 
2
2 2 4
b
a x
a a
   
    
  
ax2  bx  c الشكل النموذجي لثلاثي الحدود
a  0 ax2  bx  c  3. حل المعادلة: 0
a  0 ax2  bx  c  التالية: 0 x نعتبر المعادلة من الدرجة الثانية ذات المجهول
باستعمال الشكل النموذجي نبرهن على المبرهنة التالية:
مبرهنة
على الشكل: ax2  bx  c هي: يتم تحليل ax2  bx  c  إذا كان: حلول المعادلة 0
  0 1 2
b
x
a
  
2 ،  2
b
x
a
  
    1 2 a x  x x  x
1 2   0 2
b
x x
a

    2
1 a x  x
لا توجد حلول لا يمكن تحليل   0 2 ax  bx  c
تقبل حلا مضاعفا. ax2  bx  c  نقول أن المعادلة 0   ملاحظة: إذا كان 0
طرائق
f (x)  x2  3x  المعرف بـِ: 4 f نعتبر ثلاثي الحدود من الدرجة الثانية
f (x) 1. عين الشكل النموذجي لـِ
لدينا: x 2. بين أنه من أجل كل عدد حقيقي 25
( )
4
تقبل على قيمة حدية يطلب تحديدها. f استنتج أن . f x  
حــل:
لدينا: x 1. من أجل كل عدد حقيقي
2 2
2 3 9 3 25
3 4 4
2 4 2 4
x x x x
   
            
   
و منه
2
3 25
( )
2 4
f x x
 
    
 
. f (x) و هو الشكل النموذجي لـِ

44
2
بالعدد f (x) 2. لمقارنة 25
4
نقوم بد ا رسة إشارة الفرق  25
( )
4
f x
  
    
  
لدينا من السؤال الأول:
2
25 3
( ) ( )
4 2
f x x
 
     
 
وبما أن
2
3
0
2
x
 
   
 
نستنتج أن 25
( ) ( ) 0
4
f x   
لدينا: 25 x إذن من أجل كل عدد حقيقي
( )
4
. f x  
بما أن 25
( )
4
و f x   3 25
2 4
f
 
    
 
فإن 3
( )
2
f x f
 
   
 
تقبل على قيمة f نستنتج أن الدالة
حدية صغرى هي 25
4
و تبلغها من أجل القيمة  3
2
للمتغير. 
حل في المعادلات التالية:
x2  x  6  د( 0 x2  4x  4  جـ( 0 x2  x 1  ب( 0 x2  2x  ا( 0
نستعمل بصفة عامة المميز إلا أنه يمكن في بعض الحالات a  0 ax2  bx  c  طريقة: عند حل المعادلة 0
يقبل تحليلا ظاه ا ر. ax2  bx  c ملاحظة ما إذا كلن ثلاثي الحدود
حــل:
S 2,0 ومنه مجموعة الحلول هي x   أو 2 x  أي 0 x x  2  تعني 0 x2  2x  ا( 0
 2    ومنه c  و 1 b 1 ، a  ب( لدينا 1
S  إذن ليس للمعادلة حلول ومنه   1 4 1 1  3
  تكافئ 2 x2  4x  4  جـ( 0
S  2 ومنه x  إذن للمعادلة حل مضاعف 2 x  2  0
 2    ومنه c   و 6 b 1 ، a  د( لدينا 1
إذن للمعادلة حلان متماي ا زن:   1  4 1 6  25
1
1 25
2
2
x
 
و 2  
1 25
3
2
x
 
S 3,2 ومنه   
الدرس
المت ا رجحات من الدرجة الثانية
1. المت ا رجحة من الدرجة الثانية
كل مت ا رجحة يمكن كتابتها على أحد الشكلين ، x تعريف: نسمي مت ا رجحة من الدرجة الثانية، ذات المجهول
. a  أعداد حقيقية ثابتة مع 0 c و b ، a حيث ax2  bx  c  0 ، ax2  bx  c  التاليين: 0

43
2
a  0 ax2  bx  c : 2. إشارة ثلاثي الحدود
  0 : الحالة 1
2    لدينا
1 2 حيث: ax bx  c  a x  x x  x
1 2
b
x
a
  
و 2  2
b
x
a
  
. 
نحصل على الجدول المقابل x1  x بفرض 2
  0 : الحالة 2
2   لدينا 2
1 حيث: 1 ax bx c  a x  x 2
b
x
a

a و إشارته هي إشارة x  x من أجل 1 ax2  bx  c  ومنه 0 
. x  x من أجل كل 1
  0 : الحالة 3
لدينا
2
2
2 2 4
b
ax bx c a x
a a
    
        
   
و بما أن
2
2 0
2 4
b
x
a a
    
     
   
. a هي إشارة ax2  bx  c إشارة ، x فإن من أجل كل عدد حقيقي
مبرهنة
  0
لا تقبل حلولا ax2  bx  c  المعادلة 0
a هي من نفس إشارة ax2  bx  c إشارة ، x من أجل كل عدد حقيقي
  0
x تقبل حلا مضاعفا 1 ax2  bx  c  المعادلة 0
 1 x  x
ax2  bx  c a 0 إشارة a إشارة
  0
x و 2 x تقبل حلين متمايزين 1 ax2  bx  c  المعادلة 0
  1 2 x < x
 2 x 1 x  x
ax2  bx  c a 0 إشارة a 0 إشارة a إشارة
طرائق
حل في المت ا رجحات التالية:
x2  x  4  جـ( 0 x2 10x  25  2 ب( 0 x2  4x  6  ا( 0
 2 x 1 x  x
- 0 + + 1 x  x
- - 0 + 2 x  x
a x  x1  x  x2  a 0 إشارة a 0 إشارة a إشارة

43
-2 -1 2 3
2
-1
-2
-3
0 1
1
x
y
2
أو ax2  bx  c  0 ، ax2  bx  c  0 ، ax2  bx  c  طريقة: يؤول حل مت ا رجحة من الشكل 0
2 ax2  bx  c إلى د ا رسة إشارة ثلاثي الحدود ax  bx  c  0
حــل:
ومنه حلول المعادلة   أ( لدينا 64
2 2 هما: 5- و 1 x  4x  6  0
S   3; 1 : مجموعة الحلول هي إذن
ومنه للمعادلة   ب( لدينا 0
2 . حلا مضاعفا هو 3 x 10x  25  0
S   5 : مجموعة الحلول هي إذن
ومنه ليس للمعادلة    جـ( لدينا 15
2   حلولا لأن 0 x  x  4  0
S  : مجموعة الحلول هي إذن
f (x)  x2  x  المعرفة على بـِ: 2 f 1. باستعمال أحد ا رسمات المنحنيات مثل بيانيا الدالة
x2  x  2   2. استنتج بيانيا حلول المت ا رجحة
حــل:
1. انظر الشكل المقابل.
يقطع محور الفواصل f 2. نلاحظ أن المنحني الممثل للدالة
في نقطتين فاصلتاهما 1- و 2 على الترتيب كما نلاحظ أنه يقع
و يقع تحته من أجل x 1;2  فوق هذا المحور من أجل
لدينا إذن: . x ;1  2;
S   ;1  2; : إذن مجموعة الحلول هي
أعمال موجهة
x  3 1 
2 + 0 - 0 + 2x  4x  6
x  5 
2 - 0 - x 10x  25
x  
2 + x  x  4
x  1 2 
2 - 0 + 0 - x  3x  2

43
2
مجموع و جداء حلي معادلة من الدرجة الثانية
التالية: x نعتبر المعادلة من الدرجة الثانية ذات المجهول الحقيقي
2 a  0 مع 1 ..... ax  bx  c  0
حيث: x و x ) تقبل حلين ) جذرين 1 فإن المعادلة   نعلم أنه إذا كان 0
2 4
2
b b ac
x
a
  
و  
2 4
2
b b ac
x
a
  
 
جداؤهما بين أن: P هو مجموع الحلين و S حيث P  x x و S  x x إذا وضعنا
b
S
a
و   c
P
a

تطبيق 1: حساب أحد الحلّين بمعرفة الآخر
P أو الجداء S إذا علم أحد الجذرين يمكن حساب الجذر الآخر و ذلك باستعمال المجموع
عدد حقيقي .  2 حيث x2  x 3  تمرين تطبيقي: نعتبر المعادلة التالية: 0
حلا لهذه المعادلة ثم استنتج الحل الآخر. 3 حتىيكون  عين
تطبيق 2: تعيين عددين علم مجموعهما و جداؤهما
: x إذا و فقط إذا كانا حلين للمعادلة ذات المجهول P و جداؤهما هو S مبرهنة: يكون مجموع عددين هو
2 x  S x  P  0
أنجز برهانا لهذه المبرهنة.
.36cm 77 و محيطه cm تمرين تطبيقي: عين بعدي مستطيل مساحته 2
؟ 20cm 30 و محيطه cm هل يوجد مستطيلا مساحته 2
تطبيق 3: تعيين إشارة حلي معادلة من الدرجة الثانية
.a  0 مع 1 ..... ax2  bx  c  مبرهنة: نعتبر المعادلة: 0
1. إذا كان 0
c
a
تقبل حلين إشارتاهما مختلفتان. 1 فإن المعادلة 
2. إذا كان 0
c
a
و 0   و 0 
b
a
تقبل حلين موجبين تماما. 1 فإن المعادلة  
5. إذا كان 0
c
a
و 0   و 0 
b
a
تقبل حلين سالبين تماما. 1 فإن المعادلة  
أنجز برهانا لهذه المبرهنة.
التالية: x وجود و إشارة حلول المعادلة ذات المجهول m تمرين تطبيقي: ناقش حسب قيم الوسيط الحقيقي
    2 m1 x  2 m1 x m  0

43
أعمال موجهة
المعادلات و المت ا رجحات مضاعفة التربيع
1. المعادلات مضاعفة التربيع
ax4  bx2  c  كل معادلة يمكن كتابتها على الشكل: 0 ، x تعريف: نسمي معادلة مضاعفة التربيع، ذات المجهول
. a  أعداد حقيقية ثابتة مع 0 c و b ، a حيث
يؤول إلى حل الجملة: ax4  bx2  c  بين أن حل المعادلة 0
2
2 0
X x
aX b X c
  
   
مجهولا مساعدا. X يسمى المجهول
ax4  bx2  c  نستنتج حلول المعادلة 0 a X 2  b X  c  بعد حل المعادلة 0
التالية: x تطبيق: حل في المعادلات ذات المجهول
4 2 )1 4 2 )2 x  x  6  0 4 2 )5 x  5x  4  0 2x  5x  2  0
2. المت ا رجحات مضاعفة التربيع
كل مت ا رجحة يمكن كتابتها على أحد الشكلين التاليين: ، x تعريف: نسمي مت ا رجحة مضاعفة التربيع، ذات المجهول
4 2 . a  أعداد حقيقية ثابتة مع 0 c و b ، a حيث ax4  bx2  c  0 ، ax  bx  c  0
ax4  bx2  c يؤول حل مت ا رجحة مضاعفة التربيع إلى د ا رسة إشارة
د ا رسة مثال:
 .... x4  7x2 12  0 : x نعتبر في المت ا رجحة ذات المجهول
f (x)  x4  7x2  1. نضع: 12
X 2  7X 12  0 : X تحقق أن 5 و 4 هما حلا المعادلة ذات المجهول
f (x)  x2 3x2  4 : لدينا x 2. بين أنه من أجل كل عدد حقيقي
يمكنك استعمال جدول ( ( f (x) إشارة x 5. أدرس حسب قيم
 4. استنتج حلول المت ا رجحة
التالية: x تطبيق: حل في المت ا رجحة ذات المجهول

43
2
4 2 x  4x  5  0
مسائل محلولة
و 2 2 2 S1 1 2  ...  n : نهدف إلى حساب المجموعين التاليين
2 عدد طبيعي. n حيث S 1 2  ...  n
S 1. حساب 1
f (x 1)  f (x)  x : x من الدرجة الثانية يحقق من أجل كل عدد حقيقي f عين كثير حدود 
. n بدلالة S ثم استنتج حساب 1 S1  f (n 1)  f ( بين أن: ( 1 
أحسب مجموع الألف عدد طبيعي غير المعدومة الأولى. 
S 2. حساب 2
g(x 1)  g(x)  x2 : x من الدرجة الثالثة يحقق من أجل كل عدد حقيقي g عين كثير حدود 
ثم استنتج مجموع مربعات الألف عدد طبيعي غير المعدومة الأولى. n بدلالة S أحسب 2 
S 1. حساب 1
a  أعداد حقيقية مع 0 c و b ، a حيث f (x)  ax2  bx  c نفرض 
f (x 1)  a(x 1)2 b x 1c  ax 2  2a b x a b c : لدينا
f (x 1) f (x )  (ax 2 2a b x a b c) (ax 2 bx c)  2ax a b ومنه
إذا و فقط إذا كان: x من أجل كل عدد حقيقي f (x 1)  f (x)  x يكون
2 1
0
a
a b
 
  
أي
1
2
1
2
a
b

 
  

نجد هكذا: 1 2 1
( )
2 2
. c  ويمكن مثلا أخذ 0 f x  x  x  c
و منه 1 2 1
( )
2 2
f x  x  x
n  f (n 1)  f (n) ، ... ، 2  f (3)  f (2) ،1 f (2)  f ( نلاحظ أن ( 1 
1 2... n   f (2)  f (1) f (3)  f (2)... f (n 1)  f (n) و منه
S1  f (n 1)  f ( نجد هكذا بعد عملية الاخت ا زل: ( 1
    و f (1)  بما أن 0 2
1 1 ( 1)
( 1)
2 2
n n n n
f n
   
فإن:    ( 1)
1 2 ...
2
n n
n

   
1000 1001
1 2 ... 1000 500500
2

    
نتبع نفس الطريقة( ( S 2. حساب 2

30
2
 3 2 1 1 1
( )
3 2 6
g x  x  x  x  c
 2 2 2 ( 1)(2 1)
1 2 ...
6
n n n
n
 
   
   2 2 2 1000 1001 2001
1 2 ... 1000
6
 
   
مسائل محلولة
AB نقطة من M . AB  حيث 4 AB نعتبر دائرة قطرها
. MB و AM ننشئ الدائرتين اللتين قط ا رهما
إلى مساحة القرص a إلى مساحة الحيز الملون و بـِ S نرمز بـِ
AM  x نضع .AB الذي قطره
. x بدلالة S 1. أحسب
يكون من أجلها: M 2. هل توجد وضعية للنقطة 1
2
؟ S  a
التي يكون من أجلها: x 3. عين قيم 1
4
. S > a
x بدلالة S 1. حساب
فإن: a بـِ 2 MB و إلى مساحة القرص الذي قطره a بـِ 1 AM إذا رمزنا إلى مساحة القرص الذي قطره
1 2 S  a  a  a
لدينا:
2
4
4
2
a  
 
   
 
،
2
2
1
1
2 4
x
a   x
 
   
 
  و
2
2
2
4 1
4
2 4
x
a   x
  
    
 
ومنه:
 2 2 1 1
4 4
4 4
S     x    x
 2 4  : بعد النشر و التبسيط نجد
2
S x x

  
حيث: M 2. تعيين وضعية 1
2
S  a
1
2
 2    يكافئ S  a 1
4 4 2
2 2
x x

x2  4x  4  أي: 0 x2  4x  4  أي: 0      
  يكافئ 2 x2  4x  4  لدينا: 0
x  و منه: 2 x  2  0
التي يكون من أجلها: 1 M وضعية النقطة
2
.AB هي منتصف القطعة S  a

31
2
التي يكون من أجلها: x 3. تعيين قيم 1
4
S > a
1
4
 2    يكافئ S > a 1
4 4
2 4
x x

x2  4x  2 > أي: 0   > 
x2  4x  لندرس إشارة 2
x  2 و 2 x  2 يقبل جذرين هما: 2 x2  4x  و منه 2   لدينا 8
x 0 2 2 2 2 4
2 - 0 + 0 - x  4x  2
التي يكون من أجلها: 1 x مجموعة قيم
4
 2  2 ;2  2  : هي S > a
  .
أعمال تطبيقية
)Horner( خوارزمية هورنر
  حيث: 3 2 f نعتبر دالة كثير حدود من الدرجة الثالثة
3 2 1 0 عدد حقيقي ثابت. a و f x  x  x  x 
a 1. معاملات هورنر المرفقة بالعدد
، h2 2  ah3 ، h3  نضع: 3
1 1 2 h0 0 ah و 1 h   ah
.a معاملات هورنر المرفقة بالعدد h و 3 h2 ، h1 ، h تسمى الأعداد 0
f (a) 2. حساب
f a  h ثم استنتج أن: 0 f x   3x 2 x 1 x  تحقق أن: 0
x  a 3. التحليل باستعمال العامل
    2  : بين أن f x   f a انطلاقا من تحليل
3 2 1 0 f x  x a h x  h x  h  h
4. استعمال مجدول لتعيين معاملات هورنر
f x   2x 3  x 2 5x  المعرفة بـِ: 2 f مثال: نعتبر الدالة
تنظيم الحساب 
في a ثم نحجز قيمة E إلى غاية الخلية 1 B في خط أفقي انطلاقا مثلا من الخلية 1 f (x ) نقوم بحجز معاملات
.A و نحجز 0 في الخلية 3 A الخلية 2
 B1 B الدستور: 2 B و في الخلية 3  $A$2*A الدستور: 3 B نحجز في الخلية 2
.E ثم ننقلها بال ا زلق إلى غاية العمود B و 3 B للحصول على معاملات هورنر نحدد الخليتين 2
h0  و 0 h1 1، h2  3،h3  2 :a   نق ا ر هكذا المعاملات المرفقة بالعدد 2
0
1 ah


1
2 ah


2
3 ah

 3 
0 h 1 h 2 h 3 h

32
2
)A في الخلية 2 a 7 و 25 -) يكفي تغيير قيمة ،1.2،- حساب صور: 2 
f 25   و 30498 f 7  702 ،f 1.2  0.896 ،f (2)  لدينا: 0
x  2 باستعمال المعامل f (x ) تحليل 
f x   x  22x 2  3x 1: لدينا f 2  بما أن 0
أعمال تطبيقية
برنامج حل معادلة من الدرجة الثانية
3. مخطط البرنامج
A  مع 0 Ax 2  Bx C  التالية: 0 x نعتبر في المجموعة المعادلة ذات المجهول
D  B 2  4AC : نضع
A,B,C
نعم لا
D=0
نعم لا
D>0
X 1  B  D / 2A حل مضاعف
2
B
X
A
    2 لا توجد حلول X  B  D / 2A
Ti83plus 4. برنامج للآلة
ثم نعطي اسما للبرنامج. New في البداية نختار اللمسة ثم نختار
ثم ندخل البرنامج المقابل. Equ نسميه مثلا: 2
القيمة 0 =$A$2*A3 =B1+B2
PRGM

35
2
إرشادات
، Prompt للحصول على 
نضغط على ClrHome و Disp
I /O و نختار
 للحصول على 
نضغط على اللمسة
أو = نضغط على ثم اللمسة .  للحصول على 
،Then ، If للحصول على 
نضغط على End و Else
CTL و نختار
.3x 2  2x  3  0 ، 4x 2  4x 1 0 ، x 2  x 1 تطبيق:حل في المعادلات التالية: 0
كثي ا رت الحدود
أصحيح أم خطأ ؟
هي كثير حدود من f (x)  3x 1 2x العبارة 3
الدرجة الثالثة .
  العبارة 2
هي كثير حدود من f (x)  x  3
الدرجة الأولى .
العبارة 4
2
( )

f x 
x
هي كثير حدود .
كثيري حدود من الدرجة g(x) و f (x) إذا كان
يكون من الدرجة ال ا ربعة . f (x)  g(x) الثانية فإن
كثيري حدود من الدرجة g(x) و f (x) إذا كان
يكون من الدرجة السادسة . f (x)  g(x) الثالثة فإن
هي f في كل حالة من الحالات المقترحة أدناه الدالة
كثير حدود ؛ يطلب تعيين درجته.
)1 1
:
2
2 )2 f x  f : x 2x 1 x
2 )3 1
f : x 2x   3
x
)4
2 9
:
3


x
f x
x
2 4 2 )5 f : x x cos x  3x  xsin x  3
هو جذر x في كل حالة من الحالات المقترحة أدناه 0
. P(x) لكثير الحدود
2 )1 x0   و 1 P(x)  x  5x  6
3 2 )2 x0  و 3 P(x)  2x  5x  8x  3
4 2 )3 x0  و 3 P(x)  x  x  2x  6
في كل حالة من الحالات المقترحة أدناه كثير الحدود
يقبل جذرين متمايزين . P(x)
2 )1 P(x)  x  571x  6
2 )2 P(x)  7x  x  6
2 )3 P(x)  2x  7x  5
3 2 )4 P(x)  x  3x  5x  7
2 )5 3
( ) 6 1
2
P x  x  x 
عددان حقيقيان . b و a
x إذا كان من أجل كل عدد حقيقي
3 3 2 .a b فإن x  6x  x  (b  a)x  (b  5)x
PRGM
PRGM
2nd
STO 
MATH
1
4
5
2
3
6
7
8
9

34
أسئلة متعددة الاختيارات
عين الجواب الصحيح من بين الأجوبة المقترحة.
. P(x)  x3  3x2  x  ليكن كثير الحدود 3
. P(x) : 1( العدد 2 هو جذر لـ
. P(x) : 2( العدد 3 هو جذر لـ
لا يقبل جذور . P(x) )3
هي دالة كثير حدود من f
الدرجة الثانية ، تمثيلها البياني
موضح في الشكل المقابل.
سالب . f (x) 1( مميز
يقبل جذرين متمايزين. f (x) )2
. f (x)  0 : x 3( من أجل كل عدد حقيقي
هي إشارة معامل حدّه الذي له أعلى درجة f (x) 4( إشارة
التمثيل البياني المقابل
معرفة بـ : f لدالة
)1 2 f (x)  2x  3x 1
)2 2 f (x)  x  3x  3
)3 2 f (x)  x  3x  2
)4 2 f (x)  x  3x  2
f (x)  3x2  4x  يعطى 7
يحلل على الشكل : f (x)
)1
7
( ) 3( 1)( )
3
f x  x  x 
f (x)  (x 1)(x  7) )2
f (x)  (x 1)(7x  3) )3
(O ; i ; j) المستوي منسوب إلى معلم متعامد
هو y  x2  x  القطع المكافئ ذو المعادلة 3
بـ : y  x صورة القطع المكافئ ذي المعادلة 2
1( التناظر العمودي بالنسبة إلى محور الفواصل .
2( الانسحاب الذي شعاعه 1 11
2 4
ثم u  i  j
التناظر العمودي بالنسبة إلى محور الفواصل .
3( مركب الانسحاب الذي شعاعه 1 11
2 4
u  i  j
والتناظر العمودي بالنسبة إلى محور الفواصل .
الدوال كثيرات الحدود
. Df دالة معرفة على المجموعة f
ليس كثير حدود في كل الحالات f (x) اشرح لماذا
المقترحة .
)1 3 Df   و f (x)  2x  3x  5
)2
2 1
( )
1
x
f x
x
 


Df  1 و
)3
2
2
2 3
( )
3
x x
f x
x
  


Df  و
  )4 2
Df  و f (x)  | x |  5
من بين الدوال التالية عين الدوال كثي ا رت الحدود.
)1 2 f : x (x  3)(x  2)
  )2 2
f : x x 1  2
)3
3
2
5 10
:
2
x x
f x
x


)4 2 2 f : x 2cos x  sin x 1
كثيرة f في كل حالة من الحالات التالية ، عين دالة
الحدود من الدرجة الثانية حيث :
تأخذ قيمها موجبة تماما . f )1
.  تأخذ قيمها في المجموعة f )2
تنعدم من أجل قيمتين مختلفتين . f )3
الدالة كثير حدود حيث : f نعتبر
2 f (x)  3x  2x 1
على الشكلين التاليين: f (x) 1( تحقق من أنه يمكن كتابة
؛ (x 1)(3x 1)
2
1 4
3
3 3
x
 
    
 
يطلب تعيينهما. f 2( بين أن العدد 0 له سابقتين بالدالة
تقبل قيمة حدية عظمى على . f 3( بين أن الدالة
على . f 4( أعط اتجاه تغير الدالة
كثير حدود من الدرجة الثانية تحقق f عين دالة
الشرطين التاليين :
10
11
-1 2 3
2
-1
-2
-3
-4
0 1
1
x
y
2 3
2
3
0 1
1
x
y 12
13
14
15
18
19
16
17

33
2 ، تنعدم من أجل القيمتين 4 f
f هي صورة العدد 0 بالدالة 24
العمليات على كثيرات الحدود
على الشكل المبسط والمرتب P(x) أكتب كثير الحدود
ثم عين درجته في كل من الحالات الآتية :
11 2 P(x)  (x  3)(x  2)
12 2 P(x)  (x  5)(x  2x 1)
13 2 P(x)  (x  5)(x  3)
14 2 2 P(x)  (3x  2)  9(x  2)
كثي ا ر حدود. Q(x) و P(x) ليكن
عين في كل حالة من الحالتين التاليتين كثي ا ر حدود :
2 P(x)  3 Q(x) ؛ P(x) Q(x) ؛ P(x) Q(x)
)1 2 Q(x)  2x2  4x  و 1 P(x)  3x  x  5
)2 3 Q(x)  2x2  و 4 P(x)  2x  x  5
عين درجة ومعامل الحد الأعلى درجة لكل من كثي ا رت
الحدود التالية :
)1 2 3 P(x)  (2x  x)(5  3x )
)2 3 4 Q(x)  (3x 1) (x  3)
)3 2 3 2 2 3 R(x)  (x  x)(x  2)  x (2  2x  x )
في كل حالة من الحالات المقترحة التالية بين أن العدد
. f (x) هو جذر لكثير الحدود 
)1 3 2    و 1 f (x)  x  x  x  3
)2 3 2   و 2 f (x)  2x  x  2x 16
)3 3 2   و 3 f (x)  x  x  3x  3
حيث : P(x) نعتبر كثير الحدود
3 2 P(x)  x  x  4x  4
بحيث يكون ، من أجل c ، b ، a 1( عين الأعداد الحقيقية
. P(x)  (x 1)(ax2  bx  c) ، x كل عدد حقيقي
إلى جداء كثي ا رت الحدود من الدرجة الأولى P(x) 2( حلل
. P(x) 3( عين كل جذور
كثير الحدود حيث : P(x)
3 2 P(x)  4x  4x 15x 18
. P(x) هو جذر لِـ  1( أثبت أن 2
إلى جذاء كثي ا رت الحدود من الدرجة الأولى P(x) 2( حلل
P(x) 3( عين كل جذور
كثير حدود حيث : f (x) عددان حقيقيان و b ، a
3 f (x)  2x  ax  b
f (x) جذ ا ر لـ  بحيث يكون 2 b و a عين
. f (0)  و 5
كثير حدود حيث : f (x) أعداد حقيقية و c ، b ، a
3 2 2 f (x)  ax  3(x  b)x  cx  (x  3)x
بحيث من أجل كل عدد c ، b ، a عين الأعداد
معدوما. f (x) يكون x حقيقي
المعادلات من الدرجة الثانية
على الشكل النموذجي ، ثم f (x) أكتب كثير الحدود
في كل حالة من ، f (x)  حل في المعادلة 0
الحالات الآتية :
)1 2 f (x)  x  6x  8
)2 2 f (x)  x  x  6
)3 2 f (x)  x  3x  5
)4 2 f (x)  3x  7x  2
)5 2 4
( ) 2
5
f x  x  x 
)6 2 f (x)  5x 15x
في كل حالة من الحالات المقترحة أدناه ، أكتب
معادلة من الدرجة الثانية معاملاتها أعداد صحيحة
. x" و x' وتقبل الحلين
x"  و 5 x'  1 ؛ x"  و 3 x'  2
1
'
2
؛ x"   و 3 x  1
'
2
و x  1
"
3
x  
؛ x"  و 3 x'  0 3
'
2
x

x"  و 0 
2
20
21
22
23
24
25
28
27
26
29

33
؛ x'  x"  2 2
' "
3
x  x 
بدون حساب المميز ، حل في كلا من المعادلات
التالية : x ذات المجهول
2 )1 2 )2 x  3x  0 x  4  0
2 )3 2 )4 3x  3  0 4x  7  0
2 )5 2 )6 x  9  0 x  2x 1  0
2 )7 2 )8 x  6x  9  0 (x  3)  4
2 (4x  3)2  (3x  2)2  0 ، 2x - 2 2 x 1  0
؟ (67971 x  31527)2  ماهو مميز المعادلة 0
: x برّر أن المعادلة ذات المجهول
2 1962 x 110364 x  2007  0
تقبل حلين متمايزين .
في كل حالة من الحالات المقترحة أدناه ، حل المعادلة
: f (x) ثم استنتج تحليلا لـ f (x)  0
)1 2 f (x)  x  3 x  2
)2 2 f (x)  3x  5 x  2
)3 2 f (x)  9x  3x  2
)4 2 f (x)  5x  8 x  3
)5 2 f (x)  2x  3 x  3
التالية: x حل في كلا من المعادلات ذات المجهول
)1 2 x  3 x 10  0
)2 2 3x  5 x  2  0
)3 2 2x  7 x  8  0
)4 2 x  5 x  5  0
)5 2 x 18 x 19  0
التالية : x ذات المجهول (E) نعتبر المعادلة
2 ax  b x  c  0
غير معدوم. a أعداد حقيقية و c ، b ، a حيث
نضع '
2
b
b 
. c ، b' ، a بدلالة ، (E) مميز المعادلة ،  1( أحسب
2( نضع '
4

. c ، b' ، a بدلالة ' أحسب ،  
تقبل حلين (E) فإن المعادلة '  3( أثبت أنه إذا كان 0
b ' ' هما
a
   b ' ' ؛
a
  
)(E) يسمى المميز المختصر للمعادلة ' (
باستعمال المميز المختصر حل في كلا من
المعادلات التالية :
)1 2 x 18 x 19  0
)2 2 x  200x  9999  0
)3 2 2x  2 6 x  3  0
تمارين تطبيقـية
حل في المعادلات الآتية :
)1 2 t  5t  6  0
)2 2 u 16u 17  0
)3 2 x  (3 2) x  3 2  0
)4 2 1 r  r  0
والوسيط x ذات المجهول الحقيقي (E) نعتبر المعادلة
: m الحقيقي
2 2 2 (m  4)x  2mx  m  2m1  0
من (E) حتى تكون المعادلة m 1( عين قيم العدد الحقيقي
الدرجة الثانية
ثم (E) حتى يكون 0 حلا للمعادلة m 2( عين قيمة
استنتج الحل الآخر لها.
عدد حلول m ناقش حسب قيم الوسيط الحقيقي
في كل من الحالات التالية: x المعادلة ذات المجهول
)1 2 x  2mx  5  0
)2 2 mx  (2m 3)x  m 3  0
)3 2 (m1)x  (2m1)x  m 2  0
)4 2 (m  3)x  (2m 1)x  m  2  0
)5 2 (2m 1)x  4mx  2m 1  0
باستعمال حاسبة بيانية، حل بيانيا كلا من المعادلات
التالية :
30
31
32
34
35
36
33
39
40
37
38

33
2 2 2x  5x  3  0 x  3x 1  0
2 2 3x  6x 1  0 2x  3x  5  0
2 2 3x  3x 1  0 5x  2 10 x  2  0
m باستعمال حاسبة بيانية عين قيم العدد الحقيقي
بحيث يكون لكل من المعادلات التالية حلول في :
2 2 x  3x  m  0 2x  3x  2  m  0
2 2 2x  5x  m 1  0 3x  2 6 x  m  0
  1( أنشر العبارة 2
3 1
التالية : x 2( حل في المعادلة ذات المجهول
2 4x  2(1 3)x  3  0
f : x x2  ( 2  3)x  لتكن الدالة 6
f (x)  الهدف هو حل بطريقتين مختلفتين المعادلة 0
استنتج تحليلا لـ ؛ (x  x1 )(x  x 1( أنشر العبارة ( 2
. f (x)  ثم حل المعادلة 0 f (x)
f (x)  2( استعمل المميز لحل المعادلة 0
5( هل ينتج من كلتا الطريقتين نفس الحل ؟
في الشكل أدناه مساحة المستطيل هي 8 م ا رت مساحة
المربع ،
أحسب طول ضلع المربع.
في الشكل المقابل ، الدائرتان لهما
نفس المركز.
أحسب نصف القطر لكل منهما
بحيث تكون مساحة إحدى الدائرتين
تساوي ثلاث م ا رت مساحة الأخرى.
مثلث متقايس ABC
، 3 m الأضلاع ارتفاعه
محاط بثلاث مربعات.
  1 ـ أنشر العبارة 2
1 3
2 ـ أحسب طول ضلع المثلث ،علماٌ أن
. 12  3m مساحة الشكل الملون هي 2
نريد ملئ علبة قاعدتها مربعة الشكل بمكعبات متقايسة .
ما هو عدد المكعبات الممكنة التي تشملها
هذه العلبة حيث إذا حذفنا المكعبات الموجودة
في المحيط ، يبقى في العلبة 4 مكعبات ؟
مجموع وجداء حلي معادلة من الدرجة الثانية
في كل حالة من الحالات المقترحة أدناه ، تحقق أن
المعادلة تقبل حلين ثم بدون حساب الحلين عين مجموعهما
وجدائهما .
2 2 2x  3x  4  0 2x  3x  7  0
2 2 x  7x 1  0 x  4x  3  0
2 x  (m 1)x 1  0
2 2 x  2mx 1 m  0
: x ذات المجهول الحقيقي (E) لتكن المعادلة
2 أعداد حقيقية c ، b ، a حيث ax  bx  c  0
غير معدوم . a و
(E ') و ، (E) هما حلا المعادلة x" و x' 1( نفرض أن
x2  (x ' x")x  x ' x"  هي المعادلة 0
متكافئتان . (E ') و (E) أثبت أن المعادلتين
)لهما نفس الحلين(
x" و x' أكتب معادلة من الدرجة الثانية تقبل الحلين
في كل حالة من الحالات التالية :
x"  و 3 x'  0 x"   و 7 x'  4
و x'  3 1
"
3
و x' 1 x  2
"
3
x  
x" 1m و x' 1m
x"  5  و 2 x '  5  2
x" و x' أكتب معادلة من الدرجة الثانية تقبل حلين
42
44
12 m
5 m
45
2 cm
A 46
B C
43
47
41
48
2
50
49
51
2

33
x' x"  4 ؛ x' x"  يحققان الشرطين التاليين : 7
. x" و x' ثم عين
في كل حالة من b و a عين العددين الحقيقيين
الحالات التالية :
14
33
a b
a b
  
  
25 ؛
100
a b
a b
   
  
4 ؛
1
a b
a b
  
   
10
21
1
21
a b
a b

  
  

؛
0
49
4
a b
a b
  
   
؛
1 3
3
1
2
a b
a b
   

   
الحالات التالية : 5
8
a b
a b
  
  
4
1
a b
a b
  
   
2 7
5
a b
a b
  
   
3 8
5
a b
a b
  
  
الحالات التالية :
8
1 1 8
15
a b
a b
  
  
؛
2 2 73
24
a b
a b
  

  
| | | | 11 ؛
| | 24
a b
a b
  
  
عددين حقيقيين حيث: y ، x ليكن
3 3
17
1241
x y
x y
  
  
  1( أنشر 3
. xy ثم إستنتج قيمة ، x  y
y و x بدون حساب x2  y 2( احسب قيمة 2
. x2  7x  34  0 : (E) تعطى المعادلة
تقبل حلين غير معدومين لا (E) 1( برّر أن المعادلة
يطلب تعيينهما .
2( أكتب معادلة من الدرجة الثانية تقبل الحلين 1
x '
و 1
x "
. (E) هما حلا المعادلة x" و x' حيث
. 3x2  2x  5  0 : (E) تعطى المعادلة
مختلفين ، x" و x' تقبل حلين (E) 1( برّر أن المعادلة
في الإشارة لا يطلب تعيينهما .
؛ x ' 2 x" 2( أحسب 2 1 1
x ' x"
؛ (x ' x")2 ؛ 
4 4 x '  x"
بحيث يكون للمعادلات m عين قيم الوسيط الحققي
يحققان العلاقة المقترحة. x" و x' المعطاة أدناه ، حلان
)1 2 x'  3x" 3 و x  2mx 1  0
)2 2 4 و x  (1 m)x  2m  0 1
' "
4
. x  x 
)3 2 2 x' 2x"  و 1 (m 1)x  (1 m )x  m  0
والوسيط x ذات المجهول الحقيقي (E) لتكن المعادلة
x2  (2m  3)x  m2  2  حيث : 0 m الحقيقي
. (E) حتى يكون 1 حل للمعادلة m 1( عين قيم العدد
وجود واشارة حلول m 2( أدرس حسب قيم الوسيط
. (E) المعادلة
إن أمكن ، حتى يكون ، m عين قيم العدد الحقيقي
للمعادلات التالية ، حلان مختلفان في الإشارة:
)1 2 x  8x  5m 1  0
)2 2 2 (m1)x  (2m 3)x  m 1  0
)3 2 (m  3)x  2(m 4)x  m 2  0
)4 2 (2m 1)x  4mx 1 3m  0
إن أمكن ، حتى يكون ، m عين قيم العدد الحقيقي
للمعادلات التالية حلان موجبان:
)1 2 x  9x  3m  4  0
)2 2 mx  (3m1)x  m1  0
)5 2 (m1)x  2(m 2)x  m1  0
)4 2 (1 m)x  mx  3m  4  0
28 ومحيطه m حقل مستطيل الشكل مساحته 2
23 أحسب طولي بعديه . m
m مربع طول ضلعه ABCD
52
53
55
54
56
58
59
57
60
62
63
61

33
أحسب طول لكل من بعدي m  3cm 1( نفرض أن
ABCD المستطيل الذي محيطه هو نفس محيط
. ABCD ومساحته نصف مساحة
ABCD 2( هل يوجد مستطيل له نفس المحيط للمربع
. ABCD ومساحته أكبر تماما من مساحة المربع
بعدي المستطيل الذي له نفس مساحة m 5( أحسب بدلالة
. ABCD ومساحته هي ثلث مساحة ABCD
إشارة كثيرات الحدود
إشارة كثي ا رت x أدرس حسب قيم المتغير الحقيقي
الحدود المقترحة في الحالات التالية :
. P(x)  (x  2)(2x 1) )1
. P(x)  (3  2x)(x 1) )2
. P(x)  (x 1)(x  2)(x  3) )5
)4 2 2 . P(x)  (x  3)(x  2)
)3 4 . P(x)  x 1
)3 2 . P(x)  3x  7x
)3 3 2 P(x)  2x  3x
)1 2 . P(x)  2x  x  6
)2 2 . P(x)  3x  8x  4
)5 2 . P(x)  6x  x  2
)4 2 . P(x)  5x  x 1
)3 2 . P(x)  2x  6 2 x  9
)3 2 . P(x)  5x  2 15 x  3
)3 2 . P(x)  x 12x  36
)3 2 . P(x)  x  2 3 x  3
)3 2 1
( ) 9
2
. P x  x  x 
)1 3 2 . P(x)  2x  3 x  2x  3
)2 3 2 . P(x)  x  2 x  6x  5
)5 3 2 . P(x)  x  4 x  5x  2
)4 3 2 . P(x)  3x 11x 12x  4
)3 4 3 2 . P(x)  x 3x  x  3x
ثم أدرس إشارته حسب قيم المتغير P(x) حلل
في كل حالة من الحالات التالية : x الحقيقي
)1 4 2 . P(x)  x  3 x  2
)2 4 2 . P(x)  x  3 x  4
)5 4 2 . P(x)  3x  2 x 8
4 3 2 P(x)  2x  7x  9 x  21x  9
و 1 P( أحسب ( 3 
2
P
 
 
 
P(x) ثم حلل
. x حسب قيم المتغير الحقيقي P(x) استنتج إشارة 
عدد حلول كلا m ناقش حسب قيم الوسيط الحقيقي
الآتية : x من المعادلات ذات المجهول
)1 2 . (m1)x  3mx  m1  0
)2 2 . (1 2m)x  2mx  m  2  0
)5 2 . mx  (m1)x  m 2  0
)4 3 2 (m1)x  (5  m)x  (6  m)x  2  m  0
( ) f كثير حدود . أدرس f هو التمثيل البياني للدالة C
في f (x) إشارة ، x بيانيا ، حسب قيم المتغير الحقيقي
كل من الشكلين التاليين :
حل في كلا من المت ا رجحات التالية :
)1 2 2x  5x  3  0
)2 2 3x  5x  2  0
)5 2 2x  x 15  0
)4 2 3x 11x 10  0
2
66
64
65
67
68
69
70
-4 -3 -2 -1 2 3 4 5
2
3
4
-1
-2
-3
0 1
1
x
y
-3 -2 -1 2 3 4
2
3
4
-1
0 1
1
x
y
( ) f C
( ) f C
71

30
)3 2 2x  x  5  0
)3 2 2x  2x  4  0
)3 2 4x  x  9  0
)3 2 x  3x  7  0
)3 2 9x  6 5 x  5  0
حل في كلا من المت ا رجحات التالية :
)1 3 2 x  x  3x  3  0
)2 3 2 2x  2x  x 1  0
)5 3 2 x  2x  x  2  0
)4 4 2 x  5x  6  0
)3 2008 1962 3x 11x 1964  0
المعادلات والمتراجحات المختلفة
المعرفة بالشكل : f نعتبر الدالة
2
2
5 11 2
( )
3 7 2
x x
f x
x x
 

 
. f 1( عين مجموعة تعريف الدالة
. f (x)  0 ، x 2( حل في المعادلة ذات المجهول
الآتية: x حل في كلا من المعادلات ذات المجهول
3 3
2 1
x x
x x


 
2 1
3 1
x x
x x


 
4 1 5
1
2 1 2 1
x x
x x

 
 
7 4
2
4 7
x x
x x
 
 
 
1 1 2
x 5 x 3 x 4
 
  
2 2 x  3  2x 1  0 8 x  x  16x 17
3x 1  x  4  3 4x  7  2  2x
x  4  2x  6 11
x حل في كلا من المت ا رجحات ذات المجهول
3x  7  x  الآتية: 3
2x  3  x 1
x  2  x  2
2 2 x  3 | x 1| 0 x  4 | x  2 | 0
4 2 x  4 | x 1| 3 | x  2 | 1  0
2 (x  2)  3(x  2)  2  0
x  5 x  6  0
x  x  6  0
2
3 7
2 0
x x
  
: x ذات المجهول (E) نريد حل في المعادلة
4 3 2 (E) . . . 3x  7x  8x  7x  3  0
(E) 1( تحقق من أن العدد 0 ليس حل للمعادلة
(E ') مكافئة للمعادلة (E) 2( برهن أن المعادلة المعادلة
حيث :
: (E ')
2
1 1
3 x 7 x 2 0
x x
   
        
   
. 3u2  7u  2  5( حل في المعادلة : 0
. (E) 4( استنتج حلول المعادلة
حيث : x كثير الحدود للمتغير الحقيقي P(x) ليكن
3 2 P(x)  4x  4( 3 1) x  (9  4 3)x  9
. P(x)  1( حل في المعادلة 0
. P(x)  2( حل في المت ا رجحة 0
: x ذات المجهول (E) لتكن المعادلة
2 ax  bx  c  0
غير معدوم. a أعداد حقيقية و c ، b ، a حيث
. x" و x' حلين هما (E) نفرض أن للمعادلة
بين أن العدد  ' 4 "
5
x  x . x" و x' محصور بين
استنتج إشارة العدد  2
' 4 " ' 4 "
5 5
x x x x
a ab ac
   
   
 
5x2  7x  3  0 : (E) : تطبيق عددي
  ماهي إشارة العدد 2
؟ x ' 4x"  7x ' 28x"15
عدد حقيقي غير معدوم ، بحيث إذا أضفنا له a
. a مقلوبه نحصل على 5 . عين العدد
72
79
73
74
75
76
78
80
81
82
77

31
A B
M
H
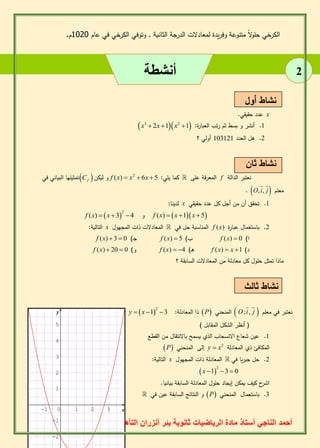
كثي ا رت الحدود
مسـائل
. قطعة مستقيمة طولها 3 [AB]
بحيث يكون : M النقطة [AB] عين على القطعة
2 MA  AB.MB  0
. AB  في نعتبر نصف الدائرة ذات القطر 8
من هذا نصف الدائرة حيث مسقطها M عين النقطة
H هو [AB] العمودي على
.MA2  3MH2  و 18
المعرفة بالشكل : 3 f نعتبر الدالة
f (x)
x
. 
في معلم متعامد f المنحني الممثل للدالة (h) نسمي
. (O ; i : j) ومتجانس
عدد نقط تقاطع m 1( ناقش حسب قيم العدد الحقيقي
ذي المعادلة (D) مع المستقيم (h) المنحني
. y  2x  m
نقطتان مشتركتان (D) و (h) 2( في الحالة التي تكون ل ـِ
منتصفات I عين مجموعة النقط ، M" و M '
. [M 'M "] القطعة
مربع طول ABCD
نقطة I ، ضلعه 1
[BD] من القطر
EBFI تعيّن مربعين
. HIGD و
بحيث يكون مجموع مساحتي I كيف يمكن اختيار النقطة
يساوي 2 HIGD و EBFI المربعين
3
.
ABCD ليكن المستطيل
AB  3 cm عرضه
. BC  5 cm وطوله
ونضع [AB] تتغير على القطعة المستقيمة M النقطة
P[AD] حيث AMNP نرسم المربع . AM  x
. NPDQ و MBRN والمستطيلين
مجموع S(x) حتى تكون x 1( عين قيم العدد الحقيقي
أكبر ما يمكن. NPDQ و MBRN مساحتي المستطيلين
تساوي نصف S(x) تكون x 2( من أجل أي قيم للعدد
. ABCD مساحة المستطيل
على بما يلي : P نعرف الدالة
2 P(x)  2x  6x  3
في مستو منسوب إلى P المنحني الممثل للدالة ( ) ليكن
. (O ; i : j) معلم متعامد ومتجانس
ذات الإحداثيتين 3 3 S لتكن النقطة
;
2 2
 
  
 
.
P(x)  a(x  b)2  c على الشكل P(x) 1( أكتب
أعداد حقيقية يطلب تعيينها. c ، b ، a حيث
ثم . (S ; i : j) في المعلم ( ) 2( أكتب معادلة للمنحني
. ( ) أرسم
ثم وضح أصغر قيمة P 5( أنجز جدول تغي ا رت الدالة
على . P للدالة
. x[ إذا كان[ 2 ; 3 P(x) 4( أعط حص ا ر للعدد
. P(x)  x 3( حل في المت ا رجحة
المستقيم ذي المعادلة (O ; i : j) 3( مثل بيانيا في المعلم
. P(x)  x ثم تحقق بيانيا من نتائج المت ا رجحة y  x
ثلاث دوال معرفة على بـِ : h ، g ، f
2 ؛ g(x)  f (| x |) ؛ f (x)  x  2x  3
h(x) | f (x) |
على h ، g ، f منحيات الدوال Ch ، Cg ، Cf ليكن
الترتيب ، الممثلة في مستو منسوب إلى معلم متعامد
. (O ; i : j) ومتجانس
؟ Cf انطلاقا من Cg زوجية ، كيف يستنتج g 1( بين أن
83
84
85
86
87
88
89
A
D
G
C
F
E B
I
H
x
A
C B
D P
N
R
Q M
2

32
الشكل f (x) يمكن كتابة ( . f 2( أدرس تغي ا رت الدالة
النموذجي(
على . g 5( استنتج تغي ا رت الدالة
. x حسب قيم العدد الحقيقي f (x) 4( عين إشارة
بدون رمز القيمة المطلقة. h(x) 3( اكتب
في نفس الرسم . Ch ، Cg ، Cf 3( ارسم المنحنيات

الحدوديات جدع مشترك علمي

More Related Content

What's hot

Viewers also liked

Similar to الحدوديات جدع مشترك علمي

More from AHMED ENNAJI

Recently uploaded

الحدوديات جدع مشترك علمي