الكتاب يتناول موضوع الرياضيات للمرحلة الإعدادية ويتضمن خمسة فصول تغطي مواضيع أساسية مثل الدوال، المعادلات، المثلثات، الهندسة، والإحصاء. يُستخدم كمرجع للطلاب ويتضمن أمثلة تطبيقية تهدف لتسهيل فهم المحتويات. الهدف منه هو تعزيز مهارات الطلاب في المادة وتحضيرهم للمواضيع المتقدمة.

1. ‫اق‬‫ﺮ‬‫اﻟﻌ‬ ‫ﺟﻤﻬﻮرﻳﺔ‬
‫اﻟﺘﺮﺑﻴﺔ‬ ‫ارة‬‫ز‬‫و‬
‫ﻟﻠﻤﻨﺎﻫﺞ‬ ‫اﻟﻌﺎﻣﺔ‬ ‫اﻟﻤﺪﻳﺮﻳﺔ‬
‫اﻷدﺑﻲ‬ ‫اﺑﻊ‬‫ﺮ‬‫اﻟ‬
‫ﺗــﺄﻟــﻴﻒ‬
‫ﺍﻟﺤﺪﻳﺜﻲ‬ ‫ﺭﺟﺐ‬ ‫ﺷﻌﺒﺎﻥ‬ ‫ﻃﺎﺭﻕ‬ / ‫ﺍﻟﺪﻛﺘﻮﺭ‬
‫ﺍﻟﺠﻮﺍﻫﺮﻱ‬ ‫ﺍﻟﻐﻔﻮﺭ‬ ‫ﻋﺒﺪ‬ ‫ﻣﺤﻤﺪ‬
‫ﺍﻟﻤﻌﻤﺎﺭ‬ ‫ﺷﺮﻳﻒ‬ ‫ﻳﻮﺳﻒ‬
‫٥١٠٢م‬ / ‫٦٣٤١ﻫـ‬ ‫اﻟﺜﺎﻣﻨﺔ‬ ‫اﻟﻄﺒﻌﺔ‬

2. ‫ﺍﻟﻄﺒﻊ‬ ‫ﻋﻠﻰ‬ ‫ﺍﻟﻌﻠﻤﻲ‬ ‫ﺍﻟﻤﺸﺮﻑ‬
‫ﻣﻌﻴﻮﻑ‬ ‫ﺣﻤﻮﺩ‬ ‫ﺷﺎﻛﺮ‬
‫ﺍﻟﻄﺒﻊ‬ ‫ﻋﻠﻰ‬ ‫ﺍﻟﻔﻨﻲ‬ ‫ﺍﻟﻤﺸﺮﻑ‬
‫ﻛﺎﻃﻊ‬ ‫ﺍﻟﺴﺎﺩﺓ‬ ‫ﻋﺒﺪ‬ ‫ﺷﻴﻤﺎﺀ‬

3. :‫مقدمة‬
‫اسة‬‫ر‬‫الد‬ ‫لطلبة‬ ‫الرياضيات‬ ‫كتب‬ ‫سلسلة‬ ‫يف‬ ‫األول‬ ‫الكتاب‬ ‫هذا‬ ‫عد‬ُ‫ي‬
‫معتمدين‬ ‫والتدرج‬ ‫األمثلة‬ ‫كرثة‬ ‫إعداده‬ ‫يف‬ ‫روعي‬ ‫وقد‬ ‫األديب‬ ‫للفرع‬ ‫اإلعدادية‬
. ‫الرياضيات‬ ‫مادة‬ ‫يف‬ ‫حصيلة‬ ‫من‬ ‫الطالب‬ ‫لدى‬ ‫ما‬ ‫عىل‬
: ‫هي‬ ‫فصول‬ ‫خمسة‬ ‫الكتاب‬ ‫هذا‬ ‫شمل‬
. ‫العددية‬ ‫التطبيقات‬ ‫وبعض‬ ‫ومتثيلها‬ ‫الدالة‬ ‫مفهوم‬ ‫يتضمن‬ : ‫األول‬ ‫الفصل‬
. ‫اجحات‬‫رت‬‫وامل‬ ‫املعادالت‬ ‫يتضمن‬ : ‫الثاين‬ ‫الفصل‬
. ‫املثلثات‬ ‫حساب‬ ‫مبادئ‬ ‫يف‬ ‫أولية‬ ‫معلومات‬ ‫يتضمن‬ : ‫الثالث‬ ‫الفصل‬
. ‫اإلحداثية‬ ‫الهندسة‬ ‫مجال‬ ‫يف‬ ‫أساسية‬ ‫مفاهيم‬ ‫يتضمن‬ : ‫ابع‬‫ر‬‫ال‬ ‫الفصل‬
‫درسه‬ ‫ملا‬ ً‫ا‬‫امتداد‬ ‫جاء‬ ‫الذي‬ ‫الوصفي‬ ‫اإلحصاء‬ ‫يتضمن‬ : ‫الخامس‬ ‫الفصل‬
. ‫املتوسطة‬ ‫املرحلة‬ ‫يف‬ ‫الطالب‬
‫العزيز‬ ‫اق‬‫ر‬‫الع‬ ‫لبلدنا‬ ‫الخري‬ ‫فيه‬ ‫ملا‬ ‫يوفقنا‬ ‫إن‬ ‫الله‬ ‫من‬ ‫نرجو‬ ‫الختام‬ ‫يف‬
... ‫املوفق‬ ‫والله‬ ‫التطوير‬ ‫بهدف‬ ‫مبالحظاتهم‬ ‫موافاتنا‬ ‫زمالئنا‬ ‫من‬ ‫ونأمل‬
‫املؤلفون‬

4. ‫الحقيقية‬ ‫الدوال‬ : ‫األول‬ ‫الفصل‬
. (‫اجعة‬‫ر‬‫م‬ ) ‫الدالة‬ ‫مفهوم‬ [ 1 - 1 ]
. ‫للدالة‬ ‫الرياﴈ‬ ‫التعبري‬ [ 1 - 2 ]
. ‫الحقيقية‬ ‫الدوال‬ [ 1 - 3 ]
. ‫للدوال‬ ‫البياين‬ ‫التمثيل‬ [ 1 - 4 ]
. ‫التﻐري‬ [ 1 - 5 ]
. ‫الطردي‬ ‫التﻐري‬ -
. ‫العكﴘ‬ ‫التﻐري‬ -
. ‫املﺸرتك‬ ‫التﻐري‬ -

5. 5
‫اﻟﺤﻘﻴﻘﻴﺔ‬ ‫اﻟﺪوال‬ : ‫اﻷول‬ ‫اﻟﻔﺼﻞ‬
: ‫اﻵﻲﺗ‬ ‫بالتعريﻒ‬ ‫وعرفناها‬ ‫الدالة‬ ‫السابقة‬ ‫املرحلة‬ ‫يف‬ ‫درسنا‬
‫من‬ ‫عنﴫ‬ ‫كل‬ ‫كان‬ ‫اذا‬ ‫دالة‬ ‫انها‬ (B) ‫مجموعة‬ ‫اﱃ‬ (A) ‫مجموعة‬ ‫من‬ ‫لعالقة‬ ‫يقال‬
‫املحددة‬ ‫املرتبة‬ ‫االزواج‬ ‫احد‬ ‫يف‬ ‫فقﻂ‬ ‫واحدة‬ ‫،مرة‬ ‫اول‬ ‫كمسقﻂ‬ ‫يظهر‬ (A) ‫عناﴏ‬
. ‫العالقة‬ ‫لبيان‬
: ‫املخطﻂ‬ ‫الحﻆ‬
‫بينﺎﻤ‬
‫دالة‬ ‫دالة‬ ‫ليسﺖ‬
‫ذلﻚ‬ ‫نكتب‬ ‫فاننا‬ ( f ) ‫بالرمز‬ ‫لها‬ ‫ورمزنا‬ (B) ‫مجموعة‬ ‫اﱃ‬ (A) ‫مجموعة‬ ‫من‬ ‫دالة‬ ‫كونﺖ‬ ‫اذا‬
: ‫اﻵتية‬ ‫الرمزية‬ ‫بالصيﻐة‬
( B ‫اﱃ‬ A ‫من‬ ‫دالة‬ f ) ‫ا‬‫ر‬‫وتق‬ f : A B
. [ ( x ,y ) f ‫أو‬ ] ‫وحيد‬ y = f(x) B ‫يوجد‬ ،∀ x A ‫حيث‬
:( 1 - 1 ) ‫تعريﻒ‬
‫للدالة‬ ‫الرياﴈ‬ ‫التعبري‬ [1-2]
: Mathematical Expression of the Function
‫بينﺎﻤ‬
‫دالة‬ ‫دالة‬ ‫ليسﺖ‬
‫بينﺎﻤ‬
‫دالة‬ ‫دالة‬ ‫ليسﺖ‬
‫بينﺎﻤ‬
‫دالة‬ ‫دالة‬ ‫ليسﺖ‬‫دالة‬ ‫دالة‬ ‫ليسﺖ‬
: ( ‫اجعة‬‫ر‬‫م‬ ) Concept of the Function ‫الدالة‬ ‫مفهوم‬ [1-1]
B BA A

6. 6
. f ‫الدالة‬ ‫بيان‬ ‫اﱃ‬ ‫ينتمي‬ ( x , y ) Ordered Pair ‫املرتب‬ ‫الزوج‬ ‫كان‬ ‫إذا‬ .1
f(x) =y ‫حيث‬
. f ‫الدالة‬ ‫تاثري‬ ‫تحﺖ‬ x ‫العنﴫ‬ Image ‫صورة‬ ‫هو‬ (y) ‫حيث‬
: ‫هي‬ ‫متيزها‬ ‫مكونات‬ ‫ثالث‬ ‫علمﺖ‬ ‫اذا‬ (f) ‫الدالة‬ ‫تتعﻦﻴ‬ .2
(x) ‫املتﻐري‬ ‫اليها‬ ‫ينتمي‬ ‫التي‬ ‫املجموعة‬ ‫وهي‬ (A) ‫املجموعة‬ ‫ومتثله‬ : Domain ‫املجال‬ (‫أ‬
. f ‫الدالة‬ ‫بيان‬ ‫اﱃ‬ ‫ينتمي‬ ( x , y ) ‫كان‬ ‫اذا‬
‫املتﻐري‬‫اليها‬‫ينتمي‬‫التي‬‫املجموعة‬‫وهي‬(B)‫املجموعة‬‫ومتثله‬:Codmain‫املقابل‬‫املجال‬ (‫ب‬
. f ‫الدالة‬ ‫بيان‬ ‫اﱃ‬ ‫ينتمي‬ ( x , y) ‫كان‬ ‫اذا‬ (y)
‫اي‬ (B) ‫بعناﴏ‬ (A) ‫عناﴏ‬ ‫تربﻂ‬ ‫التي‬ ‫العالقة‬ ‫وهي‬ : f ‫الدالة‬ ‫قاعدة‬ (‫جـ‬
. y = f (x )
: ‫اﻵتيتﻦﻴ‬ ‫الطريقتﻦﻴ‬ ‫باحدى‬ ‫الدالة‬ ‫قاعدة‬ ‫تعطﻰ‬ .3
. ‫مرتبة‬ ‫ازواج‬ ‫شكل‬ ‫عىل‬ ‫تكتب‬ ‫اي‬ f : A B ‫الدالة‬ ‫بيان‬ ‫ذكر‬ (‫أ‬
f = { ( x , y ) : y = f ( x ) , x ∈ A }
. (y) ‫باملتﻐري‬ ( x) ‫املتﻐري‬ ‫تربﻂ‬ ‫معادلة‬ ‫ذكر‬ (‫ب‬
: ‫مالحظة‬

7. 7 ‫املقابل‬ ‫ومجالها‬ (A) ‫مجالها‬ ‫من‬ ‫كل‬ ‫كان‬ ‫اذا‬ ‫حقيقية‬ ‫دالة‬ f : A B ‫الدالة‬ ‫تسمﻰ‬
. Real Numbers( R ) ‫الحقيقية‬ ‫االعداد‬ ‫مجموعة‬ ‫من‬ ‫خالية‬ ‫ﻏري‬ ‫جزئية‬ ‫مجموعة‬ (B)
. ‫املقابل‬ ‫املجال‬ R (1
. { x : x R , f ( x ) R } = ‫املجال‬ (2
(A) ‫اﱃ‬ ‫املنتمية‬ ‫الحقيقية‬ ‫االعداد‬ ‫مجموعة‬ ‫وهو‬ : (R) ‫يف‬ ( f ) ‫للدالة‬ ‫مجال‬ ‫اوسع‬
. f ( x ) R ‫عندها‬ ‫يكون‬ ‫والتي‬
. f ( x ) = x : ‫للدالة‬ ‫مجال‬ ‫اوسع‬ ‫جد‬
f={ x : x R , x ≥ 0 } ‫مجال‬ / ‫الحــل‬
x ≥ 0 ‫كان‬ ‫اذا‬ R ‫يف‬ ‫معرفة‬ f(x)‫تكون‬
f= { x : x R , x ≥ 0 } ‫مجال‬ ‫ان‬ ‫اي‬
‫املجال‬ ‫فان‬ ، ‫مجالها‬ ‫تحديد‬ ‫ويطلب‬ ‫دالة‬ ‫قاعدة‬ ‫تعطﻰ‬ ‫عندما‬
. (R) ‫يف‬ ‫ممكن‬ ‫مجال‬ ‫اوسع‬ ‫سيكون‬
1 ‫مثال‬
: ‫مالحظة‬
: Real Functions ‫الحقيقية‬ ‫الدوال‬ [1-3]

8. 8
.f ‫مجال‬ ‫فعﻦﻴ‬ f ( x ) = x 2
‫كانﺖ‬ ‫اذا‬
. f = { x : x R , f ( x) = x 2
R } = f ‫مجال‬ / ‫الحــل‬
. x R ‫كانﺖ‬ ‫مهﺎﻤ‬ R ‫يف‬ ً‫ا‬‫دوم‬ ‫معرفة‬ x 2
‫ولكن‬
R = f ‫مجال‬
. [ R ‫هو‬ f ‫للدالة‬ ‫مجال‬ ‫فاوسع‬ ‫الحدود‬ ‫كثرية‬ f ( x )‫كانﺖ‬ ‫اذا‬ : ‫نقول‬ ‫ان‬ ‫ﻤﻳكن‬ ]
f (x) = ‫قاعدتها‬ ‫التي‬ ‫الدالة‬ ‫مجال‬ ‫جد‬
. f = { x : x R , f (x) = R } ‫مجال‬ / ‫الحل‬
. x =1 ‫باستثناء‬ ‫الحقيقية‬ ‫االعداد‬ ‫كل‬ ‫يف‬ ‫معرفة‬ ‫ولكن‬
. f = R / { 1} ‫مجال‬
‫دالة‬ f : R R ‫كان‬ ‫اذا‬
(x, f ( x)) ‫النقﻂ‬ ‫مجموعة‬ ‫انه‬ ‫عىل‬ f(x) = y ‫الدالة‬ ‫منحني‬ ‫يعرف‬
. Cartesian Plane ‫الديكارﻲﺗ‬ ‫املستوي‬ ‫يف‬
x+ 2
x - 1
3 ‫مثال‬
: ‫للدوال‬ ‫البياين‬ ‫التمثيل‬ [1-4]
: (1 - 2 ) ‫تعريﻒ‬
x + 2
x - 1
x + 2
x - 1
2 ‫مثال‬

9. 9
‫بحيث‬ f : R R ‫الدالة‬ ‫متثيل‬ : ً‫ال‬‫او‬
f (x ) = a x + c , a , c R a ≠ 0
. x R ‫حيث‬ f(x) = 3 x - 6 ‫الدالة‬ ‫منحني‬ ‫ارسم‬
‫من‬ ‫نهاﻲﺋ‬ ‫ال‬ ‫بعدد‬ ‫تتحقق‬ f (x) = 3x – 6 ‫ان‬ ‫الواضﺢ‬ ‫من‬ / ‫الحل‬
( x , f (x) ) ‫املرتبة‬ ‫االزواج‬
: ‫االزواج‬ ‫هذه‬ ‫لبعض‬ ‫اﻵﻲﺗ‬ ‫والجدول‬
( 1-1 ) ‫الﺸكل‬ ‫يف‬ ‫املوضﺢ‬ ‫البياين‬ ‫املخطﻂ‬ ‫يف‬ ‫النقاط‬ ‫هذه‬ ‫رسمﺖ‬ ‫وقد‬
........- 2-1210x
........-12-90-3-6y
y
x
1 2 3 4 5 6-3 -2 -1
-1
-2
-3
-4
-5
-6
-7
-8
-9
x
x
x
(2 , 0 ) ‫ﺀ‬
(
‫1(أ‬ , -3 )
( 0 , -6 )
(-1,-9)‫ﺏ‬ x
( 1-1 ) ‫الﺸكل‬
4 ‫مثال‬
‫أ‬

10. 10
‫الـدالة‬ ‫منحني‬ ‫رسم‬ ‫ﻤﻳكن‬ ‫وعليه‬ ‫مستقيم‬ ‫معادلة‬ ‫هي‬ y = 3x - 6 ‫ان‬ ‫الحﻆ‬
‫بينهﺎﻤ‬ ‫ونصل‬ ‫املرتبة‬ ‫االزواج‬ ‫من‬ ‫زوجﻦﻴ‬ ‫باي‬ x R ‫حيث‬ f (x) = 3 x - 6
‫ينتميان‬ ( -1 , -9 ) , ( 1 , -3 ) ‫املرتبان‬ ‫فالزوجان‬ ‫ذلﻚ‬ ‫وعىل‬ ‫فقﻂ‬ ‫واحد‬ ‫مبستقيم‬
. ‫املطلوب‬ ‫املستقيم‬ ‫هو‬ ‫ب‬ ‫واملستقيم‬ ‫ب‬ ، ‫النقطتﻦﻴ‬ ‫وتعينان‬ ‫الدالة‬ ‫منحني‬ ‫اﱃ‬
‫اخريتﻦﻴ‬ ‫نقطتﻦﻴ‬ ‫اي‬ ‫او‬ ( 2 , 0 ) , ( 0 , -6 ) ‫النقطتﻦﻴ‬ ‫اخذ‬ ‫املمكن‬ ‫من‬ ‫انه‬ ً‫ا‬‫أيض‬ ‫ويالحﻆ‬
.‫االحداثيﻦﻴ‬ ‫املحورين‬ ‫مع‬ ‫املستقيم‬ ‫تقاﻃع‬ ‫نقطتي‬ ‫تعيﻦﻴ‬ ‫االحيان‬ ‫اﻏلب‬ ‫يف‬ ‫.ويفضل‬ ‫عليه‬
. ً‫ا‬‫بياني‬ f (x) = 1 - 2x ‫بحيث‬ f : R R ‫الدالة‬‫ّﻞ‬‫ﺜ‬‫ﻣ‬
. ‫مستقيم‬ ‫هو‬ ‫الدالة‬ ‫لهذه‬ ‫البياين‬ ‫التمثيل‬ ‫ان‬ / ‫الحــل‬
y= f (1) = -1 ‫فان‬ x = 1 ‫أخذنا‬ ‫واذا‬
y= f (2) = -3 ‫فان‬ x = 2 ‫أخذنا‬ ‫واذا‬
‫وتعينان‬ ‫الدالة‬ ‫بيان‬ ‫اﱃ‬ ‫ينتميان‬ ( 2 , -3 ) ‫ب‬ ، (1 , - 1) ‫املرتبان‬ ‫فالزوجان‬ ‫ذلﻚ‬ ‫وعىل‬
. ‫املطلوب‬ ‫املستقيم‬ ‫هو‬ ‫ب‬ ‫املستقيم‬ ‫ويكون‬ ‫ب‬ ، ‫النقطتﻦﻴ‬
: ‫مالحظة‬
5 ‫مثال‬

11. 11
‫يف‬ ‫كﺎﻤ‬ . ‫اخريتﻦﻴ‬ ‫نقطتﻦﻴ‬ ‫او‬ ( , 0 ) ، ( 0 , 1 ) ‫النقطتﻦﻴ‬ ‫اخذ‬ ‫املمكن‬ ‫من‬ ‫كان‬ ‫انه‬ ‫ويالحﻆ‬
. ( 1 – 2) ‫الﺸكل‬
‫حيث‬ f (x) =a x 2
+ b ‫بحيث‬ f : R R ‫للدالة‬ ‫البياين‬ ‫التمثيل‬ : ً‫ا‬‫ثاني‬
. ً‫ا‬‫منحني‬ ‫متثل‬ ‫وهي‬ a ≠ 0 ‫وان‬ a ، b R
. ً‫ا‬‫بياني‬f (x) = x2
‫بحيث‬ f : R R ‫الدالة‬ ‫ل‬ّ‫ث‬‫م‬
. ‫الحقيقية‬ ‫االعداد‬ ‫مجموعة‬ ‫هو‬ ‫الدالة‬ ‫هذه‬ ‫مجال‬ ‫ان‬ / ‫الحــل‬
‫النصﻒ‬ ‫يف‬ ‫يقع‬ ‫الدالة‬ ‫لهذه‬ ‫البياين‬ ‫التمثيل‬ ‫فان‬ ‫ذلﻚ‬ ‫وعىل‬
. ‫االحداﻲﺛ‬ ‫املستوي‬ ‫من‬ ‫فقﻂ‬ ‫االعىل‬
‫الدالة‬ ‫هذه‬ ‫منحني‬ ‫نقﻂ‬ ‫بعض‬ ‫لنا‬ ‫يعﻦﻴ‬ ‫اﻵﻲﺗ‬ ‫والجدول‬
≡
y
X
( 1-2 ) ‫الﺸكل‬
(2 ,-3 )‫ب‬
1
2
.....103210-1-2-3....x
.....102
9410149....y
6 ‫مثال‬
( 0 , 1 ) ( , 0 )
x
x
x
(1 ,-1 )
1
2x

12. 12
‫التي‬ ‫النقاط‬ ‫وبعض‬ ‫الجدول‬ ‫هذا‬ ‫يف‬ ‫الواردة‬ ‫املرتبة‬ ‫لالزواج‬ ‫املمثلة‬ ‫النقﻂ‬ ‫تعيﻦﻴ‬ ‫وﻤﻳكن‬
‫هو‬ ‫املنحني‬ ‫هذا‬ ‫يكون‬ ‫مبنحني‬ ‫النقاط‬ ‫هذه‬ ‫بﻦﻴ‬ ‫صل‬ ‫ثم‬ y = x2
‫املعادلة‬ ‫احداثياتها‬ ‫تحقق‬
. ( 1 – 3 ) ‫بالﺸكل‬ ‫موضﺢ‬ ‫هو‬ ‫كﺎﻤ‬ ‫الدالة‬ ‫لهذه‬ ‫البياين‬ ‫التمثيل‬
‫نقطة‬ ‫كل‬ ‫صورة‬ ‫ان‬ ‫مبعنﻰ‬ . ‫الصادات‬ ‫محور‬ ‫حول‬ ‫متناﻇر‬ ‫املنحني‬ ‫هذا‬ ‫ان‬ ‫ويالحﻆ‬
‫النقطة‬ ‫هي‬ ‫الصادات‬ ‫محور‬ ‫يف‬ ‫انعكاس‬ ‫تاثري‬ ‫تحﺖ‬ ‫الدالة‬ ‫منحني‬ ‫اﱃ‬ ‫تنتمي‬ ( x, y )
y = x2
‫الدالة‬ ‫ملنحني‬ ‫البياين‬ ‫التمثيل‬ ‫ان‬ . ً‫ا‬‫ايض‬ ‫الدالة‬ ‫منحني‬ ‫اﱃ‬ ‫تنتمي‬ (- x , y )َ
. ( parabola ً‫ا‬‫مكافﺌ‬ ً‫ا‬‫قطع‬ ) ‫يسمﻰ‬
. ً‫ا‬‫بياني‬ y = x2
+ 3 ‫بحيث‬ f : R R ‫الدالة‬ ‫ل‬ّ‫ث‬‫م‬
y = x2
+ 3 / ‫الحــل‬
‫بانسحاب‬ y = x 2
‫للدالة‬ ‫املمثل‬ ‫املنحني‬ ‫عن‬ ‫ينتﺞ‬ ‫ان‬ ‫ﻤﻳكن‬ ‫الدالة‬ ‫لهذه‬ ‫املمثل‬ ‫املنحي‬ ‫ان‬
‫والجدول‬ ‫وحدات‬ 3 ‫مبقدار‬ ‫الصادات‬ ‫ملحور‬ ‫املوجب‬ ‫االتجاه‬ ‫يف‬ ‫االعىل‬ ‫اﱃ‬ ‫نقطة‬ ‫كل‬ ‫ينقل‬
: ‫الدالة‬ ‫هذه‬ ‫منحني‬ ‫نقﻂ‬ ‫بعض‬ ‫لنا‬ ‫يعﻦﻴ‬ ‫اﻵﻲﺗ‬
y
( 1-3 ) ‫الﺸكل‬
x
(1 , 1 )
x
xx( -1 , 1 )
(-2 , 4 ) (2 , 4 )
X
7 ‫مثال‬

13. 13
‫البياين‬ ‫التمثيل‬ ‫لنا‬ ‫ينتﺞ‬ ‫مبنحني‬ ‫ووصلها‬ ‫الناتجة‬ ‫املرتبة‬ ‫لﻸزواج‬ ‫املمثلة‬ ‫النقاط‬ ‫بتحديد‬
. ( 1 - 4 ) ‫الﺸكل‬ ‫يف‬ ‫كﺎﻤ‬ ‫للمحني‬
(0, 3 )
(0 , 0)
.....210-1-2x
.....74347y
X
y
( 1 - 4 ) ‫الﺸكل‬
x
(1 , 4 )
x
xx(-1, 4 )
(-2 , 7 ) (2 , 7 )
x

14. 14
. ً‫ا‬‫بياني‬ y = 1 - x2
‫بحيث‬ f : R R ‫الدالة‬ ‫ل‬ّ‫ث‬‫م‬
y = 1 - x2
/ ‫الحــل‬
‫عن‬ ‫ينتﺞ‬ ‫أن‬ ‫ﻤﻳكن‬ ‫الدالة‬ ‫لهذه‬ ‫البياين‬ ‫التمثيل‬ ‫فان‬ ‫ذلﻚ‬ ‫وعىل‬ R ‫هو‬ ‫الدالة‬ ‫هذه‬ ‫مجال‬ ‫إن‬
‫ينقل‬ ‫وبانسحابه‬ ‫ومحدب‬ ‫االصل‬ ‫نقطة‬ ‫يف‬ ‫رأسه‬ ‫مكافﺊ‬ ‫قطع‬ y = - x2
‫لدالة‬ ‫املمثل‬ ‫املنحني‬
‫لنا‬ ‫يعﻦﻴ‬ ‫اﻵﻲﺗ‬ ‫والجدول‬ ‫واحدة‬ ‫وحدة‬ ‫مبقدار‬ ‫الصادات‬ ‫ملحور‬ ‫املوجب‬ ‫االتجاه‬ ‫يف‬ ‫األعىل‬ ‫إﱃ‬
: ‫الدالة‬ ‫هذه‬ ‫منحني‬ ‫نقﻂ‬ ‫بعض‬
xx
x x
x
y
( -1 , 0 )
x
( 0, 1 )
(1 , 0 )
( 2 , -3 )
( 1-5 ) ‫الﺸكل‬
y
.....210-1-2x
.....-3010-3y
8 ‫مثال‬
(- 2 , -3 )

15. 15
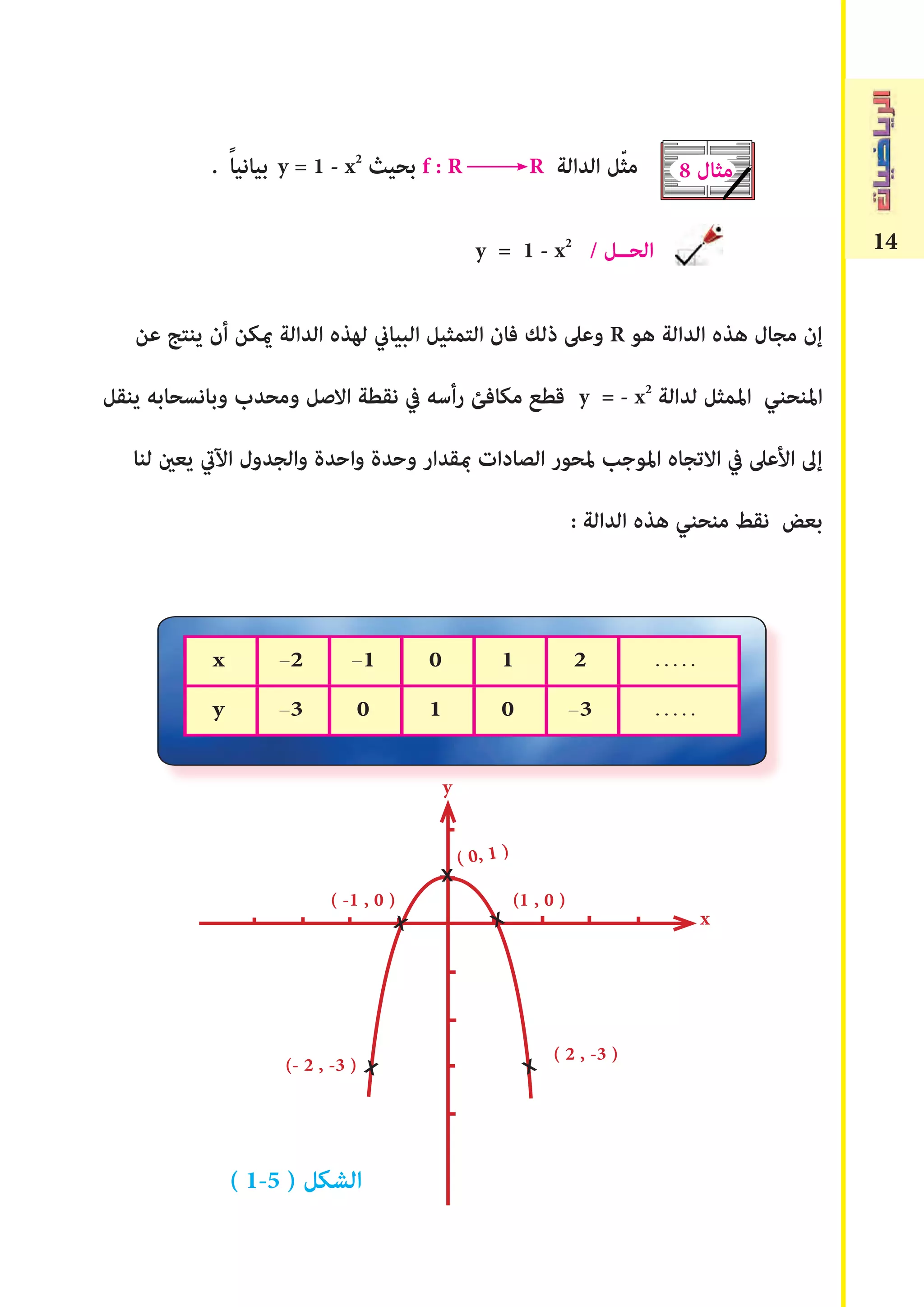
: ‫اﻵتية‬ ‫الدوال‬ ‫من‬ ‫كل‬ ‫منحنيات‬ ‫ارسم‬ (1
f ( x ) = - 4 x + 3 ( ‫أ‬
f ( x ) = -3 (‫ب‬
f ( x ) = 4 – x2
( ‫جـ‬
f( x ) = -2x 2
( ‫د‬
f ( x ) = x 2
– 4 ( ‫هـ‬
: ‫اﻵتية‬ ‫الدوال‬ ‫من‬ ٌ‫كل‬ ‫مجال‬ ‫جد‬ (2
f ( x ) = x3
+ x2
- 3 ( ‫أ‬
f ( x ) = (‫ب‬
f ( x ) = 4 - x ( ‫جـ‬
f ( x ) = x + 2 ( ‫د‬
f ( x ) = y = x + 1 ‫بحيث‬ f : R R ‫ليكن‬ (3
. f ( -3 ) , f(2) , f [ f (-1) ] , f ( 1 + ∆x ) , f ( a+2 ) , f ( b -3 ) ‫جد‬
2x + 6
x2
-x -6
(1-1) ‫متارين‬

16. 16
‫ففي‬ .‫معنية‬ ‫بعالقة‬ ‫يرتبﻂ‬ ‫ات‬‫ري‬‫املتﻐ‬ ‫من‬ ً‫ا‬‫زوج‬ ‫نجد‬ ‫ما‬ ً‫ا‬‫ري‬‫كث‬ ‫للرياضيات‬ ‫استخدامنا‬ ‫عند‬
‫هذا‬ ‫حصل‬ ‫املتﻐريين‬ ‫احد‬ ‫عىل‬ ‫تﻐري‬ ‫اي‬ ‫حصل‬ ‫اذا‬ ‫التي‬ ‫بالصورة‬ ‫العالقة‬ ‫تكون‬ ‫االحيان‬ ‫بعض‬
. ‫اﻵخر‬ ‫املتﻐري‬ ‫يف‬ ‫نفسها‬ ‫بالنسبة‬ ‫التﻐري‬
: ‫الطردي‬ ‫التﻐري‬ : ً‫ال‬‫او‬
( ‫موجب‬ ‫حقيقي‬ ‫عدد‬ k ) ً‫ا‬‫موجب‬ ً‫ا‬‫ثابت‬ ً‫ا‬‫عدد‬ k ‫وان‬ ، ‫متﻐريين‬ x ، y ‫كان‬ ‫اذا‬
‫وتكتب‬ ( x ) ‫لـ‬ ً‫ا‬‫تبع‬ ً‫ا‬‫ﻃردي‬ ‫تتﻐري‬ y : ‫نقول‬ ‫فاننا‬ y = k x ‫وكان‬
y x
. x ‫مع‬ Direct proportionً‫ا‬‫ﻃردي‬ ‫تتناسب‬ y : ‫وتقرأ‬
. ( ‫املستقل‬ ‫املتﻐري‬ ) x ‫ويسمﻰ‬
. ( ‫التابع‬ ‫املتﻐري‬ ) y ‫ويسمﻰ‬
‫يكون‬ ‫عندما‬ y = 15 ‫وكان‬ (x) ‫لـ‬ ً‫ا‬‫تبع‬ ً‫ا‬‫ﻃردي‬ ‫يتﻐري‬ y ‫كان‬ ‫اذا‬
. y = 30 ‫يكون‬ ‫عندما‬ x ‫قيمة‬ ‫فجد‬ x = 7
y x / ‫الحــل‬
k R +
,‫ثابﺖ‬ k ‫ان‬ ‫حيث‬ y = k x
15 = k(7) ⇒ k =
: ( 1- 3 ) ‫تعريﻒ‬
∝
9 ‫مثال‬
∝
: Variation ‫التــــﻐيــر‬ [1-5]
15
‫ـــــ‬
7

17. 17
y 1
y 2
y 1
x 1
y 2
x 2
y 1
x 1
4.8
1.6
y 2
x 2
15
5
y 1
x 1
y 2
x 2
∝
x 1
x 2
10 ‫مثال‬
15
7
x = = 14 ∴
‫القيمتﻦﻴ‬ x ‫اخذت‬ ‫فان‬ ‫ما‬ ‫بعالقة‬ ‫مرتبطان‬ ‫حقيقيان‬ ‫ان‬‫ري‬‫متﻐ‬ x ، y
15 ، 4.8 ‫هﺎﻤ‬ x ‫لقيمتي‬ ‫املناﻇرتﻦﻴ‬ y ‫قيمتا‬ ‫وكانﺖ‬ 5 ، 1.6
‫؟‬ ‫ﻃردي‬ ‫تﻐري‬ ‫عالقة‬ x ، y ‫بﻦﻴ‬ ‫العالقة‬ ‫فهل‬
∵ x1
= 1.6 , x2
= 5 = = 3 / ‫الحــل‬
y1
= 4.8 , y2
= 15 = = 3
=
. ‫ﻃردي‬ ‫تﻐري‬ ‫عالقة‬ x ، y ‫بﻦﻴ‬ ‫العالقة‬ ∴
y = x ∴
: ‫ياﻲﺗ‬ ‫ما‬ ‫نستنتﺞ‬ (1-3) ‫التعريﻒ‬ ‫من‬
y ‫اخذ‬ ‫لذلﻚ‬ ً‫ا‬‫وتبع‬ x1
، x2
‫القيمتﻦﻴ‬ x ‫املتﻐري‬ ‫واخذ‬ y x ‫كان‬ ‫اذا‬
: ‫فان‬ ‫الرتتيب‬ ‫عىل‬ y1
، y2
‫القيمتﻦﻴ‬
= ‫او‬ =
30 × 7
15

18. 18
: ‫مالحظة‬
≠ ‫كان‬ ‫اذا‬ ‫اما‬
. ‫ﻃردي‬ ‫تﻐري‬ ‫عالقة‬ ‫ليسﺖ‬ x ، y ‫بﻦﻴ‬ ‫فالعالقة‬
: ‫العكﴘ‬ ‫التﻐري‬ ً‫ا‬‫ثاني‬
‫وكان‬ ( ‫موجب‬ ‫حقيقي‬ ‫عدد‬ k ) ‫ثابﺖ‬ ‫عدد‬ k ‫وان‬ ،‫متﻐريين‬ y ، x ‫كان‬ ‫اذا‬
‫ونكتب‬ ( x ) ‫لـ‬ ً‫ا‬‫تبع‬ ً‫ا‬‫عكسي‬ ‫تتﻐري‬ y : ‫نقول‬ ‫فاننا‬ y = k .
، x ‫مع‬Inverse proportion ً‫ا‬‫عكسي‬ ‫تتناسب‬ y : ‫وتقرأ‬ y
. ( ‫التابع‬ ‫املتﻐري‬ ) y ‫ويسمﻰ‬ ( ‫املستقل‬ ‫املتﻐري‬ ) x ‫ويسمﻰ‬
y = 3 ، x = 20 ‫وكانﺖ‬ (x ) ‫لـ‬ ً‫ا‬‫تبع‬ ً‫ا‬‫عكسي‬ ‫تتﻐري‬ y ‫كانﺖ‬ ‫اذا‬
. x = 6 ‫عندما‬ y ‫قيمة‬ ‫فاوجد‬
y / ‫الحــل‬
∴ y = , k R +
3 = k = 60
∴ y = = = 10
y 1
x 1
y 2
x 2
1
x
∝
∝
: ( 1 - 4 ) ‫تعريﻒ‬
11 ‫مثال‬
k
x
k
20
60
x
1
x
1
x
⇐
60
6

19. 19
: ‫ماياﻲﺗ‬ ‫نستنتﺞ‬ ( 1-4) ‫تعريﻒ‬ ‫من‬
y ‫اخذ‬ ‫لذلﻚ‬ ً‫ا‬‫وتبع‬ x1
، x2
‫القيمتﻦﻴ‬ x ‫املتﻐري‬ ‫واخذ‬ y ‫كان‬ ‫اذا‬
: ‫فان‬ ‫الرتتيب‬ ‫عىل‬ y1
، y2
‫القيمتﻦﻴ‬
= ‫او‬ =
y ، x ‫ان‬‫ري‬‫املتﻐ‬ ‫اخذ‬ ‫فاذا‬ ‫ما‬ ‫بعالقة‬ ‫مرتبطان‬ ‫حقيقيان‬ ‫ان‬‫ري‬‫متﻐ‬ x ، y
‫ونقﺺ‬ 35 ‫اصبﺢ‬ ‫حتﻰ‬ x ‫املتﻐري‬ ‫قيمة‬ ‫ادت‬‫ز‬‫و‬ ‫الرتتيب‬ ‫عىل‬ 21 ، 15 ‫القيمتﻦﻴ‬
‫؟‬ y ‫هل‬ 8 ‫فاصبﺢ‬ y ‫املتﻐري‬ ‫لذلﻚ‬ ً‫ا‬‫تبع‬
= = , x1
= 3 , x2
= 7 /‫الحــل‬
= , y1
= 21 , y2
= 8
∵ ≠
. ( x ) ‫لـ‬ ً‫ا‬‫تبع‬ ً‫ا‬‫عكسي‬ ‫تتﻐري‬ ‫ال‬ y ∴
x z ‫ان‬ ‫عىل‬ ‫فﱪهن‬ y , x ‫كانﺖ‬ ‫اذا‬
x x = k R / ‫الﱪهان‬
y y = h R +
∴ x = = R +
∴ x z
y 1
y 2
x 2
x 1
∝
x 2
x 1
35
15
7
3
∝1
z
∝ 1
y ⇐
k
y
x 2
x 1
y 1
y 2
y 1
y 2
21
8
y 1
x 2
y 2
x 1
12 ‫مثال‬
∝
13 ‫مثال‬
∝
1
x
1
x
1
y
∝∝
,
∝ 1
z
⇐ h
z
,
k
y
k
h
k
h
,
+
z

20. 20
: ‫املﺸرتك‬ ‫التﻐري‬ : ً‫ا‬‫ثالث‬
: ‫كان‬ ‫فاذا‬ ، ‫ات‬‫ري‬‫متﻐ‬ ‫ثالث‬ x ، y ، z ‫كانﺖ‬ ‫اذا‬
‫ومنها‬ x ‫فنكتب‬ z ‫تبع‬ ً‫ا‬‫وعكسي‬ y ‫تبع‬ ً‫ا‬‫ﻃردي‬ ‫تتﻐري‬ x ( ‫أ‬
.x = k k R +
x = k z y ‫ومنها‬ x y z ‫فنكتب‬ y ، z ‫تبع‬ ً‫ا‬‫ﻃردي‬ ‫تتﻐري‬ x (‫ب‬
. ( ‫ثابﺖ‬ k ) ‫ان‬ ‫حيث‬
x = ‫ومنها‬ x ‫فنكتب‬ y ، z ‫تبع‬ ً‫ا‬‫عكسي‬ ‫تتﻐري‬ x (‫جـ‬
. ( ‫ثابﺖ‬ k ) ‫ان‬ ‫حيث‬
، x = 3 ‫عندما‬ y = 24 ‫وكانﺖ‬ x، z ‫تبع‬ ً‫ا‬‫ﻃردي‬ ‫تتﻐري‬ y ‫كانﺖ‬ ‫اذا‬
. y = 30 ، z = 15 ‫عندما‬ x ‫قيمة‬ ‫جد‬ z = 4
y x z / ‫الحــل‬
y = k x z k R +
24 = k (3)(4)
∴ k = 2
∴ y = 2 x z
30 = 2 x(15) ⇒ x =1
∝
y
z∝
1
y z
y
z
: ( 1 - 5 ) ‫تعريﻒ‬
14 ‫مثال‬
,
∝
∝
k
y z
,

21. 21
. a2
+ b2
ab ‫ان‬ ‫عىل‬ ‫برهن‬ a b ‫كان‬ ‫اذا‬
∵ a b / ‫الحــل‬
∴ a = k b , k R +
a2
+ b2
= ab ‫ان‬ ‫نثبﺖ‬ ‫ان‬ ‫يجب‬ a 2
+ b2
ab ‫ان‬ ‫ثبات‬ ‫وال‬
= h ( ‫ثابﺖ‬ )
= =
=h R+
a2
+ b 2
ab∴
y = 7 ‫كان‬ ‫فاذا‬ . x ، z ‫مع‬ ً‫ا‬‫مﺸرتك‬ ً‫ا‬‫عكسي‬ ً‫ا‬‫ري‬‫تﻐ‬ ‫تتﻐري‬ y ‫كان‬ ‫اذا‬
. ‫التﻐري‬ ‫ثابﺖ‬ ‫جد‬ x= 1 ، z = 3 ‫عندما‬
y . y = k . , k ∈ R+
/ ‫الحـــل‬
7 = k . ⇒k = 21
∝
k2
b2
+ b2
k b × b
b2
( k2
+1 )
k . b2
k2
+ 1
k
∝
a 2
+ b2
ab
15 ‫مثال‬
16 ‫مثال‬
∝
1
x
1
x z
1
(1)(3)
∝
∝
∝(h)
a 2
+ b2
ab
1
z

22. 22
‫قيمة‬ ‫جد‬ x = 5 ‫عندما‬ y = 10 ‫وكان‬ x ‫مع‬ ً‫ا‬‫ﻃردي‬ ‫تتﻐري‬ y ‫كانﺖ‬ ‫اذا‬ (1
. x = 15 ‫عندما‬ y
‫جد‬ y =25 ‫عندما‬ x = 16 ‫وكان‬ x ‫مع‬ ً‫ا‬‫عكسي‬ ‫يتﻐري‬ y ‫كانﺖ‬ ‫اذا‬ (2
. x = 20 ‫عندما‬ y ‫قيمة‬
x = 1 ‫عندما‬ y = 4 ‫وكان‬ x ، y ‫مع‬ ً‫ا‬‫مﺸرتك‬ ً‫ا‬‫ري‬‫تﻐ‬ ‫يتﻐري‬ z ‫كان‬ ‫اذا‬ (3
. ‫التﻐري‬ ‫ثابﺖ‬ ‫جد‬ z =2
‫كان‬ ‫فاذا‬ ً‫ا‬‫مﺸرتك‬ ً‫ا‬‫ري‬‫تﻐ‬ L ‫مع‬ ً‫ا‬‫وعكسي‬ x ‫مع‬ ً‫ا‬‫ﻃردي‬ ‫يتﻐري‬ y ‫كان‬ ‫اذا‬ (4
‫للعالقة‬ ‫رياضية‬ ‫صيﻐة‬ ‫جد‬ x = 2 ، L = 4 ‫عندما‬ y =
. y ، x ، L ‫بﻦﻴ‬
. y x ‫فاثبﺖ‬ x y ‫كان‬ ‫اذا‬ (‫أ‬ (5
. x z ‫ان‬ ‫فاثبﺖ‬ x y ، y z ‫كان‬ ‫اذا‬ (‫ب‬
R +
‫منها‬ ‫لكل‬ ‫التعويض‬ ‫مجموعة‬ ‫حقيقيﻦﻴ‬ ‫متﻐريين‬ x ، y ‫كان‬ ‫اذا‬ (6
. x3
+ y3
x2
y ‫ان‬ ‫فاثبﺖ‬ y x ‫وكان‬
y = 10 ‫عندما‬ x = 24 ‫وكانﺖ‬ y - 1 ‫تبع‬ ‫عكسيا‬ x ‫تﻐريت‬ ‫اذا‬ (7
‫؟‬ y = 5 ‫عندما‬ x ‫قيمة‬ ‫فﺎﻤ‬
. x ‫قيمة‬ ‫فجد‬ . 15 = ‫التﻐري‬ ‫وثابﺖ‬ y = 5 ‫كان‬ ‫فاذا‬ . x ‫تبع‬ ً‫ا‬‫عكسي‬ ‫يتﻐري‬ y ‫كان‬ ‫اذا‬ (8
3
2
∝
(1-2) ‫متارين‬
∝
∝∝∝
∝ ∝

23. 2323
. ‫املعادالت‬ [2-1 ]
. ‫متهيد‬ -
‫بطريقتي‬ ‫الثانية‬ ‫الدرجة‬ ‫معادلة‬ ‫حل‬ -
. ‫التحليل‬ *
. ‫الدستور‬ *
. ‫الحقيقية‬ ‫ات‬‫رت‬‫الف‬ [ 2-2]
‫الحقيقي‬ ‫للعدد‬ ‫املطلقة‬ ‫القيمة‬ [2-3]
. ‫اجحة‬‫رت‬‫امل‬ [2-4]
. ‫متهيد‬ -
‫االوﱃ‬ ‫الدرجة‬ ‫من‬ ‫اجحات‬‫رت‬‫امل‬ ‫حل‬ -
. ‫مطلق‬ ‫عىل‬ ‫تحتوي‬ ‫واحد‬ ‫متﻐري‬ ‫يف‬
. ‫متﻐريين‬ ‫يف‬ ‫الثانية‬ ‫الدرجة‬ ‫من‬ ‫املعادالت‬ ‫حل‬ [2-5]
. ‫بالتعويض‬ -
. ‫بالحذف‬ -
: ‫الثاني‬ ‫الفصل‬
‫اجحات‬‫ر‬‫والمت‬ ‫المعادالت‬

24. 24
‫املاضية‬ ‫السنوات‬ ‫(ويف‬ function )‫الدالة‬ ‫معنﻰ‬ ‫االول‬ ‫الفصل‬ ‫يف‬ ‫درسﺖ‬ ‫ان‬ ‫سبق‬
‫متﻐريين‬ ‫ويف‬ ‫واحد‬ ‫متﻐري‬ ‫يف‬ ‫االوﱃ‬ ‫الدرجة‬ ‫(من‬ equation ) ‫املعادلة‬ ‫حل‬ ‫مجموعة‬ ‫إيجاد‬
‫املعادلتﻦﻴ‬ ‫ان‬ ‫عرفﺖ‬ ‫كﺎﻤ‬ ‫واحد‬ ‫متﻐري‬ ‫يف‬ ‫الثانية‬ ‫الدرجة‬ ‫من‬ ‫املعادلة‬ ‫حلول‬ ‫مجموعة‬ ‫وكذلﻚ‬
‫نفسها‬ ‫التعويض‬ ‫ومجموعة‬ ‫نفسها‬ ‫الحل‬ ‫مجموعة‬ ‫لهﺎﻤ‬ ‫اللتان‬ ‫املعادلتان‬ ‫هﺎﻤ‬ ‫املتكافﺌتﻦﻴ‬
. R ‫تعويضها‬ ‫مجموعة‬ ‫فان‬ ‫للمعادلة‬ ‫التعويض‬ ‫مجموعة‬ ‫تذكر‬ ‫ﻢﻟ‬ ‫اذا‬ ‫انه‬ ‫حينها‬ ‫يف‬ ‫وقلنا‬
.‫متكافﺌتﻦﻴ‬‫ليستا‬ x – 1 = 0 ، x2
–1=0 ‫فاملعادلتان‬
. ‫متكافﺌتان‬ 2x + 3 = 5 ، 2x = 2 ‫املعادلتان‬ ‫أما‬
‫متكافﺌتﻦﻴ‬ ‫ليستا‬ x ∈ Z ‫،حيث‬ x + 3 = 0 x ∈ N ‫،حيث‬ x + 3 = 0 ‫واملعادلتان‬
. ‫وهكذا‬ ....
‫ما‬ ‫معادلة‬ ‫عىل‬ ‫تجري‬ ‫التي‬ ‫ال‬‫ز‬‫واالخت‬ ‫والتجميع‬ ‫التبديل‬ ‫خواص‬ ‫ان‬ ‫هو‬ ‫ذكره‬ ‫يجدر‬ ‫ومﺎﻤ‬
. ‫لها‬ ‫مكافﺌة‬ ‫معادلة‬ ‫اﱃ‬ ‫تؤدي‬
‫عن‬ ‫حلولها‬ ‫مجموعة‬ ‫تختلﻒ‬ ‫معادلة‬ ‫عىل‬ ‫ونحصل‬ ‫ما‬ ‫معادلة‬ ‫عىل‬ ‫معينة‬ ‫بعملية‬ ‫نقوم‬ ‫وقد‬
. ‫االصلية‬ ‫املعادلة‬
‫الطرفﻦﻴ‬ ‫برتبيع‬ x2
= 1 ‫وان‬ x = 1 ‫فان‬ x – 1 = 0 ‫كان‬ ‫اذا‬ ً‫ال‬‫فمث‬
. ‫للطرفﻦﻴ‬ (1 ) ‫للعدد‬ ‫الجمعي‬ ‫النظري‬ ‫باضافة‬ x2
– 1 = 0
( ‫بالتحليل‬ ) ( x – 1 ) ( x + 1 ) = 0
x = -1 ‫أو‬ x = 1
R ‫ﻓﻲ‬ ‫واﳌﺘﺮاﺟﺤﺎت‬ ‫اﳌﻌﺎدﻻت‬ : ‫اﻟﺜﺎﻧﻲ‬ ‫اﻟﻔﺼﻞ‬
: ‫ﲤﻬﻴﺪ‬ [2-1-1]
: �e Equations ‫املعادالت‬ [2-1]

25. 25
. { -1 , 1 } ‫هي‬ x2
– 1 = 0 ‫املعادلة‬ ‫حلول‬ ‫مجموعة‬ ∴
‫مجموعتان‬ ‫وهﺎﻤ‬ { 1 } ‫هي‬ ‫االصلية‬ ‫للمعادلة‬ ‫الحلول‬ ‫مجموعة‬ ‫ان‬ ‫نجد‬ ‫وبسهولة‬
‫اﱃ‬ ‫تنتمي‬ ‫التي‬ ‫الجذور‬ ‫ومعرفة‬ ‫الحل‬ ‫بتحقيق‬ ‫يقوم‬ ‫ان‬ ‫الطالب‬ ‫ننصﺢ‬ ‫لذا‬ ‫مختلفتان‬
.ً ‫انفا‬ ‫ذكرناها‬ ‫التي‬ ‫الخواص‬ ‫ﻏري‬ ‫عمليات‬ ‫اجرى‬ ‫اذا‬ ‫األصلية‬ ‫املعادلة‬ ‫حلول‬ ‫مجموعة‬
: ‫الﺸكل‬ ‫من‬ ‫معادلة‬ ‫هي‬ ‫واحد‬ ‫متﻐري‬ ‫يف‬ ‫الثانية‬ ‫الدرجة‬ ‫معادلة‬ ‫ان‬ ‫تعلمﺖ‬
a ≠ 0 ‫حيث‬ ax2
+ b x + c = 0
‫الﺸكل‬ ‫من‬ ‫لها‬ ‫مكافﺌة‬ ‫معادلة‬ ‫ايجاد‬ ‫عىل‬ ‫املعادلة‬ ‫هذه‬ ‫حل‬ ‫يعتمد‬
‫بﺸكل‬ ‫بوضعها‬ ‫عنها‬ ‫ناتجة‬ ‫معادلة‬ ‫اﱃ‬ ‫اي‬ ‫ذلﻚ‬ ‫امكن‬ ‫ان‬ ( mx – d ) ( n x – e ) = 0
‫مجموعة‬ ‫بخواص‬ ‫معلوماتنا‬ ‫اﱃ‬ ً ‫استنادا‬ ‫و‬ ‫االوﱃ‬ ‫الدرجة‬ ‫من‬ ‫الحدود‬ ‫كثريﻲﺗ‬ ‫ﴐب‬ ‫حاصل‬
: ‫نكتب‬ ‫ان‬ ‫ﻤﻳكننا‬ ‫الحقيقية‬ ‫االعداد‬
m x – d = 0 x =
( m x – d) ( n x – e ) = 0 ‫أو‬ ⇒
n x – e = 0 x =
: ‫هي‬ ‫املفروضة‬ ‫الثانية‬ ‫الدرجة‬ ‫من‬ ‫املعادلة‬ ‫حل‬ ‫مجموعة‬ ‫ان‬ ‫ونقول‬
{ , }
: ‫واﺣﺪ‬ ‫ﻣﺘﻐﻴﺮ‬ ‫ﻓﻲ‬ ‫اﻟﺜﺎﻧﻴﺔ‬ ‫اﻟﺪرﺟﺔ‬ ‫ﻣﻌﺎدﻟﺔ‬ ‫ﺣﻞ‬ [2 - 1 - 2]
Factoring ‫اﻟﺘﺤﻠﻴﻞ‬ : ً‫ﻻ‬‫او‬
d
m
e
n
{
d
m
e
n

26. 26
x2
– 7 x + 6 = 0 : ‫املعادلة‬ ‫حل‬
x2
– 7 x + 6 = 0 ( x – 1 ) ( x – 6 ) = 0 / ‫الحــل‬
x – 6 = 0 ‫أو‬ x – 1 = 0 ‫اما‬
x =6 ‫أو‬ x = 1
. { 6 , 1 } = ‫هي‬ ‫املعادلة‬ ‫حل‬ ‫مجموعة‬ ‫وتكون‬
x2
= 49 ‫املعادلة‬ ‫حل‬ ‫مجموعة‬ ‫جد‬
x2
– 49 =0 ( x – 7 ) ( x + 7 ) = 0 / ‫الحــل‬
x + 7 = 0 ‫أو‬ x – 7 = 0 ‫اما‬
x = - 7 ‫أو‬ x = 7
{ -7 , 7 } = ‫مﺞ‬
: ‫هي‬ ‫واحد‬ ‫متﻐري‬ ‫يف‬ ‫الثانية‬ ‫الدرجة‬ ‫من‬ ‫ملعادلة‬ ‫القياسية‬ ‫الصيﻐة‬
a ≠ 0 ‫حيث‬ ax2
+ b x + c = 0
: ‫املعادلة‬ ‫كتابة‬ ‫ﻤﻳكن‬ . ( ‫لالﻃالع‬ ) ‫املربع‬ ‫اكﺎﻤل‬ ‫ﻃريقة‬ ‫وباستخدام‬
a x2
+ b x + c = a ( x2
+ x + ) = 0 ..... 1
1 ‫للمعادلة‬ ‫االيﴪ‬ ‫الطرف‬ ‫(اﱃ‬ )2
‫املقدار‬ ‫وﻃرحنا‬ ‫اضفنا‬ ‫ولو‬
1 ‫مثال‬
2 ‫مثال‬
‫اﻟﺪﺳﺘﻮر‬ : ً‫ﺎ‬‫ﺛﺎﻧﻴ‬
b
a
〇
c
a
b
2a
〇

27. 27
a [ x2
+ x + ( )2
] + [ - ( )2
] = 0 ‫ينتﺞ‬
a [ x + ] 2
+ [ ] = 0 , a ≠ 0
( x + )2
=
x + = + ‫ينتﺞ‬ ‫الطرفﻦﻴ‬ ‫بجذر‬
‫نوع‬ ‫معرفة‬ ‫بواسطته‬ ‫وﻤﻳكن‬ ‫املميز‬ ‫باملقدار‬ b2
- 4ac ‫املقدار‬ ‫يسمﻰ‬
: ‫هو‬ ‫بالدستور‬ a x2
+ b x + c = 0 ‫املعادلة‬ ‫حل‬ ‫ويكون‬ ‫املعادلة‬ ‫حل‬ ‫اﱃ‬ ‫الحاجة‬ ‫دون‬ ‫ان‬‫ر‬‫الجذ‬
. ‫الدستور‬ ‫بطريقة‬ 2x2
– 3 x = 1 ‫املعادلة‬ ‫حل‬
2x2
– 3x – 1 = 0 ⇒ a = 2 ، b = -3 ، c = -1 / ‫الحــل‬
b2
– 4 a c ⇒ 9 - 4 (2) ( -1) = 17 ∈ R = ‫املميز‬
: 0 ‫من‬ ‫اكﱪ‬ ‫املميز‬ ‫قيمة‬ ‫الن‬ ‫الدستور‬ ‫تطبيق‬ ‫ﻤﻳكن‬
x = ⇒ x =
{ , } = ‫مﺞ‬
4 a c - b2
4 a 2
b2
- 4 a c
4 a 2
{ , }
b
a
c
a
b
2 a
√
3 ‫مثال‬
3 + 17
4
√
b
2 a
b
2 a
b
2 a
b
2 a
b2
- 4 a c
2 a
b + b2
- 4a c
2a
√x=
b - b2
- 4a c
2a
√b + b2
- 4a c
2a
√
b + b2
- 4 a c
2 a
√
3 - 17
4
√ 3 + 17
4
√

28. 28
. ‫الدستور‬ ‫باستخدام‬ 4x2
– 4x + 1 = 0 ‫املعادلة‬ ‫حل‬
4x2
- 4x+1=0 ⇒ a = 4 , b = -4 , c = 1 / ‫الحــل‬
‫املميز‬ = b2
– 4 a c
=( - 4 )2
– 4 (4 )(1 )
= 16 – 16
= 0
‫الدستور‬ ‫تطبيق‬ ‫ﻤﻳكن‬ ∴
x = ⇒ x =
x =
. { } = ‫مﺞ‬ ∴ ‫متساويان‬ ‫ان‬‫ر‬‫الجذ‬
‫املعادلة‬ ‫ا‬‫ر‬‫جذ‬ ‫فان‬ b2
- 4 a c = 0 ‫املميز‬ ‫قيمة‬ ‫كانﺖ‬ ‫اذا‬
: ‫فان‬ ‫متساويان‬ a x2
+ b x + c = 0
{ } = ‫مﺞ‬
4 ‫مثال‬
- ( - 4 )
2 ( 4 )
b + b2
- 4 a c
2 a
√-
1
2
1
2
: ( 1 ) ‫مالحظة‬
- b
2a
-

29. 29
‫يف‬ ‫للمعادلة‬ ‫حل‬ ‫يوجد‬ ‫فال‬ ‫صفر‬ ‫من‬ ‫اصﻐر‬ b2
– 4 a c ‫املميز‬ ‫قيمة‬ ‫كانﺖ‬ ‫اذا‬
‫الحل‬ ‫فأن‬ ‫صفر‬ ‫يساوي‬ ‫او‬ ‫من‬ ‫أكﱪ‬ ‫قيمته‬ ‫كانﺖ‬ ‫إذا‬ ‫أما‬ . R ‫الحقيقية‬ ‫االعداد‬ ‫مجموعة‬
. R ‫اﱃ‬ ‫ينتمي‬
R ‫يف‬ ‫حل‬ ‫لها‬ ‫ليس‬ x2
- 2 x + 5 = 0 : ‫املعادلة‬ : ‫مثال‬
b2
– 4 ac = (-2)2
- 4 ( 1) ( 5 ) ‫الن‬
= 4- 20
= -16 < 0
: ( 2 ) ‫مالحظة‬
: ‫مثال‬

30. 30
: ‫التحليل‬ ‫ﻃريقة‬ ً‫ا‬‫مستخدم‬ ‫اﻵتية‬ ‫املعادالت‬ ‫حلول‬ ‫مجموعة‬ ‫جد‬(1
6x2
+ 7x – 3 = 0 (‫أ‬
2x2
+ 3x – 9 = 0 (‫ب‬
x2
+ 12 = 7x (‫جـ‬
( ‫الحل‬ ‫صحة‬ ‫حقق‬ ) x- x– 12 = 0 x > 0 (‫د‬
x6
+ 7x3
= 8 (‫هـ‬
‫اﻵتية‬ ‫املعادالت‬ ‫حلول‬ ‫مجموعة‬ ‫جد‬ ‫ثم‬ ‫اﻵتية‬ ‫املعادالت‬ ‫جذري‬ ‫نوع‬ ‫بﻦﻴ‬ (2
.( ‫الدستور‬ ) ‫القانون‬ ً‫ا‬‫مستخدم‬
3x2
– 7x + 2 = 0 (‫أ‬
3x2
– 7x + 4 = 0 (‫ب‬
4x2
+ 9 = 12x (‫جـ‬
x2
– 4 x + 5 = 0 (‫د‬
√
(2-1) ‫متارين‬
,

31. 31
: ‫االعداد‬ ‫مجموعة‬ ‫تسمﻰ‬ – 1
‫حيث‬ b ‫اﱃ‬ a‫من‬ ( closed Interval ) ‫املﻐلقة‬ ‫الفرتة‬ { x : x ∈ R ، a ≤ x ≤ b }
‫رمزنا‬ ‫حيث‬ ( 2 - 1) ‫الﺸكل‬ ‫يف‬ ‫كﺎﻤ‬ ‫االعداد‬ ‫خﻂ‬ ‫عىل‬ ‫ومتثل‬ [a , b] ‫بالرمز‬ ‫لها‬ ‫ونرمز‬ a < b
‫لهذه‬ ‫النهاية‬ ‫ولنقطة‬ a ‫باحداثيها‬ ‫املﻐلقة‬ ‫الفرتة‬ ‫متثل‬ ‫التي‬ ‫املستقيمة‬ ‫للقطعة‬ ‫البداية‬ ‫لنقطة‬
(o) ‫االصل‬ ‫نقطة‬ ‫ذكر‬ ‫الﺸكل‬ ‫هذا‬ ‫يف‬ ‫اهملنا‬ ‫لقد‬ b ‫باحداثيها‬ ‫القطعة‬
‫ومجموعة‬ [a , b ] ‫الفرتة‬ ‫اﱃ‬ ‫املنتمية‬ ‫الحقيقية‬ ‫االعداد‬ ‫مجموعة‬ ‫بﻦﻴ‬ ‫تقابل‬ ‫وجود‬ ‫يالحﻆ‬
. ab ‫املستقيمة‬ ‫القطعة‬ ‫نقاط‬
. a ∈ [ a , b ] , b ∈ [ a , b ] ‫حيث‬
( 2 -1 ) ‫الﺸكل‬
‫املفتوحة‬ ‫الفرتة‬ { x : x ∈ R ، a < x < b } = ( a , b ) : ‫املجموعة‬ ‫نسمي‬ - 2
‫يف‬ ‫كﺎﻤ‬ ‫الحقيقية‬ ‫االعداد‬ ‫الخﻂ‬ ‫عىل‬ ‫ومتثل‬ a < b ‫حيث‬ b ‫اﱃ‬ a ‫(من‬Open Interval)
. (2-2) ‫الﺸكل‬
( 2 - 2 ) ‫الﺸكل‬
‫يف‬ a , b‫العددين‬ ‫حول‬ ‫والدائرتان‬ a ∉ (a , b) , b ∉ (a , b ) ‫ان‬ ‫الحالة‬ ‫هذه‬ ‫يف‬ ‫ويالحﻆ‬
. ‫ذلﻚ‬ ‫عىل‬ ‫تدالن‬ ‫الﺸكل‬
a b
: Real Intervals ‫الحقيقية‬ ‫ات‬‫رت‬‫الف‬ [ 2 - 2 ]
a b

32. 32
: ‫املجموعتﻦﻴ‬ ‫من‬ ‫كال‬ ‫نسمي‬-3
{ x : x ∈ R ، a < x ≤ b } = ( a , b ]
{ x : x ∈ R ، a ≤ x < b } = [ a , b )
‫مفتوحة‬ ‫نصﻒ‬ ‫او‬ (Half - closed Interval) ‫مﻐلقة‬ ‫نصﻒ‬ ‫الفرتة‬
( 2 – 3 ) ‫الﺸكل‬ ‫يف‬ ‫كﺎﻤ‬ ‫االوﱃ‬ ‫املجموعة‬ ‫ومتثل‬ a < b ‫حيث‬ (Half - open Intetval)
‫الﺸكل‬ ‫يف‬ ‫كﺎﻤ‬ ‫الثانية‬ ‫املجموعة‬ ‫ومتثل‬ a ∉ ( a , b ] , b ∈ ( a , b ] ‫حيث‬
a ∈ [ a , b ) , b ∉ [ a , b ) ‫حيث‬ ( 2 - 4)
: ‫هي‬ ‫تساويه‬ ‫او‬ a ‫الحقيقي‬ ‫العدد‬ ‫عىل‬ ‫تزيد‬ ‫التي‬ ‫الحقيقية‬ ‫االعداد‬ ‫مجموعة‬ - 4
( 2 – 5 ) ‫الﺸكل‬ ‫يف‬ ‫كﺎﻤ‬ ‫وﻤﻧثلها‬ { x : x ∈ R ، x ≥ a }
‫تكﱪ‬ ‫التي‬ ‫الحقيقية‬ ‫االعداد‬ ‫مجموعة‬ ‫عىل‬ ‫تدل‬ { x : x ∈ R ، x > a } = ‫املجموعة‬ ‫ان‬ ‫كﺎﻤ‬
: ( 2-6 ) ‫الﺸكل‬ ‫يف‬ ‫كﺎﻤ‬ ‫ومتثلها‬a ‫الحقيقي‬ ‫العدد‬
b
( 2 - 3 ) ‫الﺸكل‬
b(2 - 4) ‫الﺸكل‬
( 2 - 5) ‫الﺸكل‬
( 2-6) ‫الﺸكل‬
a
a
a
a

33. 33
‫التي‬ ‫الحقيقية‬ ‫األعداد‬ ‫مجموعة‬ ‫عىل‬ ‫تدل‬ { x : x ∈ R ، x ≤ a } = ‫املجموعة‬ - 5
( 2 – 7 ) ‫الﺸكل‬ ‫يف‬ ‫كﺎﻤ‬ ‫وﻤﻧثلها‬ ‫اوتصﻐره‬ ‫الحقيقي‬ ‫العدد‬ ‫تساوي‬
‫هي‬ ‫التي‬ ‫الحقيقية‬ ‫االعداد‬ ‫مجموعة‬ ‫عىل‬ ‫تدل‬ {x : x ∈ R ، x < a } = ‫واملجموعة‬
( 2 – 8 ) ‫الﺸكل‬ ‫يف‬ ‫كﺎﻤ‬ ‫وﻤﻧثلها‬ a ‫الحقيقي‬ ‫العدد‬ ‫من‬ ‫اقل‬
[ 3 , 8 ] [ 1 , 6 ] ( ) ‫جد‬
[ 3 , 8 ] - [ 1 , 6 ] (‫)ب‬
[ 1 , 6 ] [ 3 , 8 ] = [ 3 , 6 ] ، [ 1 , 6 ] - [ 3 , 8 ] = [ 1 , 3 )
{ x : x > -3 } [ -5 , 2 ) ‫جد‬
{ x : x > -3 } [ -5 , 2 ) = { x : x ≥ - 5 }
1 3 6 8
-5 -3 2
( 2 - 7) ‫الﺸكل‬
( 2 - 8) ‫الﺸكل‬
6 ‫مثال‬
(2 - 9) ‫الﺸكل‬
7‫مثال‬
a
a
a

34. 3434
of

35. 35
x - 3 , x > 3
|x - 3 | = 0 , x = 3
3 - x , x < 3
: ‫اﻵتية‬ ‫بالخواص‬ ‫تتمتع‬ ‫املطلقة‬ ‫القيمة‬ ‫ان‬ ( 2 – 1 ) ‫التعريﻒ‬ ‫من‬ ‫نستنتﺞ‬
1) ∀ x R , | x | ≥ 0
- 5 R , | - 5 | = 5 > 0 ً‫ال‬‫مث‬
0 R , | 0 | = 0
2) ∀x R , | -x | = |x |
9 = | -9 | = | 9 | ً‫ال‬‫مث‬
3) ∀ x R , - | x| ≤ x ≤ | x |
|6 | = 6 > -|6 | ‫مثال‬
4) ∀ x R , x2
= | x | 2
( -3 )2
= |-3| 2 ً‫ال‬‫مث‬
9 = ( 3 )2
= 9
5) ∀x ، y R , | x . y | = | x | . | y |
x = 3 ، y = - 5
| 3 ( -5 ) | = | 3 | . | -5 |
| -15 | = ( 3 ) ( 5 )
15 = 15
{

36. 36
6 ) - a ≤ x ≤ a ‫فان‬ |x| ≤ a ‫كان‬ ‫اذا‬ a > 0 ‫حيث‬
-7 ≤ x ≤ 7 ‫فان‬ | x | ≤ 7 ‫كان‬ ‫اذا‬
7 ) ∀x ، y ∈ R ‫فان‬ | x + y | ≤ | x | + | y |
x = 3 ، y = 5 ( ‫مثال‬
| 3 + 5 | = | 3 | + | 5 |
8 = 8
x = 3 ، y = -5 (‫ب‬
| 3 + (- 5) | < | 3| + | - 5 |
| - 2 | < 3 + 5
2 < 8

37. 37
‫ات‬‫رت‬‫الف‬ ‫من‬ ‫كل‬ ‫يف‬ ‫عناﴏ‬ ‫خمسة‬ ‫اكتب‬ (1
( -10 , -6 ] ، ( -1 , 1] ، ( , ] ، [ 0 , 1 ] ، [ 1 , 2 ) ، ( 3 , 4 ] ، ( 5 , 7 )
: ‫يأﻲﺗ‬ ‫ما‬ ‫جد‬ ‫الحقيقي‬ ‫للعدد‬ ‫املطلقة‬ ‫القيمة‬ ‫تعريﻒ‬ ‫باستخدام‬ (2
| -3 | ، | | ، | - 2 | ، | 3 – 5 | ، | 2 – 5 |
A = [ -3 , 1 ] , B = [ -1 , 2 ] ‫لتكن‬ (3
A∪ B ، A ∩B ، A– B ‫من‬ ‫كال‬ ‫االعداد‬ ‫خﻂ‬ ‫عىل‬ ‫مثل‬ (‫أ‬
‫حقيقية‬ ‫ات‬‫رت‬‫ف‬ ‫شكل‬ ‫عىل‬ A∪ B ، A∩B ، A – B ‫من‬ ً‫ال‬‫ك‬ ‫اكتب‬ (‫ب‬
: ‫يأﻲﺗ‬ ‫مﺎﻤ‬ ‫كال‬ ‫جد‬ (4
{ x : x ≥ -1 } ∩ [ -3 ، 2 ) (‫أ‬
( - 3 , 1 ] ∩ { x : x > 2 } (‫ب‬
(- 2 , 3 ] ∪ { x : x < 1 } (‫جـ‬
[ - 3 , 0 ] - ( - 2 , 3 ) (‫د‬
1
4
1
2
3
7
√√
(2-2) ‫متارين‬
√

38. 38
: ‫متهيد‬ [ 2 – 4 – 1 ]
f(x) < g (x ): ‫بالﺸكل‬ ‫تكتب‬ ‫والتي‬ x ً‫ا‬‫ري‬‫متﻐ‬ ‫تحوي‬ ‫التي‬ Inequality ‫اجحة‬‫رت‬‫امل‬ ‫ان‬
. x ‫واحد‬ ‫متﻐري‬ ‫يف‬ ‫اجحة‬‫رت‬‫م‬ ‫تسمﻰ‬ ‫مفتوحان‬ ‫ان‬‫ري‬‫تعب‬ f(x) ، g (x )‫حيث‬
‫يف‬ x ‫لـ‬ ‫اعطيﺖ‬ ‫اذا‬ ‫التي‬ ‫القيم‬ ‫من‬ ‫مجموعة‬ ‫نا‬ّ‫ي‬‫ع‬ ‫اذا‬ ‫انه‬ ، ‫السابقة‬ ‫استﻚ‬‫ر‬‫د‬ ‫من‬ ‫تعلم‬ ‫وكﺎﻤ‬
‫وتعرف‬ ‫اجحة‬‫رت‬‫امل‬ ‫هذه‬ ‫حل‬ ‫مجموعة‬ ‫اوجدنا‬ ‫نقول‬ ‫صائبة‬ ‫عبارة‬ ‫وجعلها‬ ‫اجحة‬‫رت‬‫امل‬ ‫هذه‬
. ‫املتكافﺌة‬ ‫املعادالت‬ ‫عرفﺖ‬ ‫كﺎﻤ‬ ‫املتكافﺌة‬ ‫اجحات‬‫رت‬‫امل‬
h (x) < s (x ) ‫مكافﺌة‬ ‫اجحة‬‫رت‬‫م‬ f (x) < g (x ) ‫اجحة‬‫رت‬‫امل‬ ‫عن‬ ‫نقول‬
. ‫نفسها‬ ‫الحل‬ ‫مجموعة‬ ‫لهﺎﻤ‬ ‫كان‬ ‫اذا‬
. ‫الحدود‬ ‫كثرية‬ f (x) ، g (x )‫من‬ ‫كل‬ ‫فيها‬ ‫يكون‬ ‫التي‬ ‫اجحات‬‫رت‬‫امل‬ ‫بحل‬ ‫البند‬ ‫هذا‬ ‫يف‬ ‫سنهتم‬
‫واحد‬ ‫متﻐري‬ ‫يف‬ ‫االوﱃ‬ ‫الدرجة‬ ‫من‬ ‫اجحات‬‫رت‬‫امل‬ ‫حل‬ ‫املتوسﻂ‬ ‫الثالث‬ ‫الصﻒ‬ ‫يف‬ ‫درسﺖ‬ ‫وقد‬
‫لها‬ ‫مكافﺌة‬ ‫اجحات‬‫رت‬‫م‬ ‫اﱃ‬ ‫املفروضة‬ ‫اجحة‬‫رت‬‫امل‬ ‫من‬ ‫لالنتقال‬ ‫الحذف‬ ‫خواص‬ ‫استخدمنا‬ ‫وقد‬
‫حللنا‬ ‫اننا‬ ‫عندها‬ ‫ونقول‬ x > b ‫او‬ x < a : ‫الﺸكل‬ ‫من‬ ‫اجحة‬‫رت‬‫م‬ ‫اﱃ‬ ‫نصل‬ ‫حتﻰ‬ ‫التعاقب‬ ‫عىل‬
. ‫اجحة‬‫رت‬‫امل‬
: ( 2-2 ) ‫تعريﻒ‬
: Inequalities ‫اجحات‬‫رت‬‫امل‬ [ 2 - 4 ]

39. 39
‫مجموعة‬ ‫كانﺖ‬ ‫اذا‬ 3x +1< x + 5 : ‫اجحة‬‫رت‬‫للم‬ ‫الحل‬ ‫مجموعة‬ ‫جد‬
. ‫االعداد‬ ‫خﻂ‬ ‫عىل‬ ‫الحل‬ ‫مجموعة‬ ‫ومثل‬ R ‫هي‬ ‫التعويض‬
3x + 1 < x + 5 / ‫الحـــل‬
( 3x + 1 ) + ( - x ) < ( x + 5 ) + ( - x )
2x + 1 < 5
( 2x + 1 ) + ( -1 ) < 5 + ( - 1 )
2x < 4
(2x ) < (4)
x < 2
{ x : x ∈ R، x < 2 } = ‫الحل‬ ‫مجموعة‬
|x – 2 | > 5 ‫اجحة‬‫رت‬‫للم‬ ‫الحل‬ ‫مجموعة‬ ‫جد‬ ‫التعويض‬ ‫مجموعة‬ ‫هو‬ R ‫كان‬ ‫اذا‬
( x – 2 ) , x ≥ 2 / ‫الحــل‬
(2 –x ) , x < 2
| x – 2 | > 5 ⇒ x – 2 > 5 2 – x > 5
x > 7 ‫أو‬ x < -3
: ‫هي‬ ‫املطلوبة‬ ‫الحل‬ ‫مجموعة‬ ‫ان‬ ‫نجد‬ ‫النظام‬ ‫هذا‬ ‫وبحل‬
{ x : x ∈ R ، x > 7 } ∪ { x : x ∈R ، x < -3 } = 2
‫ف‬ ∪1
‫ف‬
1
2
| x – 2 | =
2
‫ف‬ 1
‫ف‬7-3
2
8 ‫مثال‬
: ‫ﻣﻄﻠﻖ‬ ‫ﻋﻠﻰ‬ ‫ﲢﺘﻮي‬ ‫اﻻوﻟﻰ‬ ‫اﻟﺪرﺟﺔ‬ ‫ﻣﻦ‬ ‫اﳌﺘﺮاﺟﺤﺎت‬ ‫ﺣﻞ‬ [ 2 - 4 - 2 ]
9 ‫مثال‬
1
2
‫أو‬

40. 40
. Elimination ‫بالحذف‬ ‫أو‬ substitution ‫بالتعويض‬ ‫الحل‬ ‫ويكون‬
‫او‬ ‫االقل‬ ‫عىل‬ ‫الثانية‬ ‫الدرجة‬ ‫من‬ ‫حد‬ ‫عىل‬ ‫املتﻐريين‬ ‫ذات‬ ‫املعادلتﻦﻴ‬ ‫احدى‬ ‫اشتملﺖ‬ ‫اذا‬
‫يف‬ ‫الثانية‬ ‫الدرجة‬ ‫من‬ ‫معادلة‬ ‫تسمﻰ‬ ‫املعادلة‬ ‫هذه‬ ‫فان‬ ‫متﻐريين‬ ‫ﴐب‬ ‫حاصل‬ ‫عىل‬ ‫اشتملﺖ‬
. ‫متﻐريين‬
. R ‫هي‬ x ، y ‫من‬ ‫لكل‬ ‫التعويض‬ ‫مجموعة‬ ‫كانﺖ‬ ‫اذا‬
‫للنظام‬ ‫الحل‬ ‫مجموعة‬ ‫جد‬ x = { 0 , 1 , 2 , 3 }
x – y = 1 .............. 1
x2
+ y = 11 .............. 2
: ‫هي‬ 1 ‫للمعادلة‬ ‫الحل‬ ‫مجموعة‬ / ‫الحــل‬
{ ( 0 , - 1 ) , (1 , 0) , ( 2 , 1 ) , ( 3 , 2 ) } = 1
‫ف‬
: ‫هي‬ 2 ‫للمعادلة‬ ‫الحل‬ ‫مجموعة‬
{ ( 0 , 11 ) , (1 , 10 ) , (2 , 7) , (3 ,2) } = 2
‫ف‬
: ‫هي‬ ‫للنظام‬ ‫الحل‬ ‫مجموعة‬ ‫فتكون‬
{ ( 3 , 2 ) } = 2
‫ف‬ ∩ 1
‫ف‬ = ‫ف‬
‫مجموعة‬ ‫جد‬ R ‫هي‬ x ، y ‫من‬ ‫لكل‬ ‫التعويض‬ ‫مجموعة‬ ‫كانﺖ‬ ‫اذا‬
.ً‫ا‬‫سابق‬ ‫املذكور‬ ‫للنظام‬ ‫الحل‬
x = y+ 1 ...... 3 : 1 ‫من‬ : ‫الجﱪية‬ ‫الطريقة‬ ‫نتبع‬ / ‫الحــل‬
: ‫ينتﺞ‬ 2 ‫يف‬ 3 ‫نعوض‬
(y + 1 )2
+ y = 11 ⇒ y2
+ 3y - 10 =0
⃝
⃝
⃝
: ‫الثانية‬ ‫الدرجة‬ ‫من‬ ( ‫متﻐريين‬ ) ‫اﻵنية‬ ‫املعادالت‬ ‫حل‬ [2-5]
10 ‫مثال‬
11 ‫مثال‬
⃝
⃝
⃝
⃝⃝

41. 41
(y+ 5) (y – 2) = 0 ⇔ y = - 5 ..... 3 ‫يف‬ ‫التعويض‬
{ (-4 , -5 ) } = 1
‫ف‬ ‫ويكون‬ x =- 4 ∴
3 ‫يف‬ ‫بالتعويض‬ y = 2 ‫أو‬
{ ( 3 , 2 ) } = 2
‫ف‬ ‫ويكون‬ x = 3 ∴
{ (-4 , -5 ) , ( 3 , 2 ) } = 2
‫ف‬ ∪ 1
‫ف‬ ‫الحل‬ ‫مجموعة‬
‫الحل‬ ‫مجموعة‬ ‫جد‬ R ‫هي‬ x ، y ‫من‬ ‫لكل‬ ‫التعويض‬ ‫مجموعة‬ ‫لنفرض‬
x2
+ y2
= 25 ............. 1 ‫للنظام‬
x2
+ y2
+ 2x + 2y = 39 .......... 2
2x + 2y = 14 ⇔ x + y = 7 : ‫ينتﺞ‬ 2 ‫من‬ 1 ‫بطرح‬ / ‫الحــل‬
∴ x = 7 - y ............. 3
: 1 ‫يف‬ 3 ‫بتعويض‬
( 7 – y )2
+ y2
= 25 ⇔ 2y2
– 14 y + 24 = 0
⇔ y2
– 7y + 12 = 0
( y – 3 ) ( y – 4 ) = 0
{ (4 , 3 ) } = 1
‫ف‬ ⇐ ∴ x = 4 3 ‫يف‬ ‫بالتعويض‬ y = 3 ‫اما‬
{ ( 3 , 4 ) } = 2
‫ف‬ ⇐ ∴ x = 3 3 ‫يف‬ ‫بالتعويض‬ y = 4 ‫او‬
{ ( 3 , 4 ) ، ( 4 , 3 ) } = 2
‫ف‬ ∪ 1
‫ف‬ ‫الحل‬ ‫مجموعة‬ ∴
⃝
⃝
⃝
⃝
⃝
⃝
12 ‫مثال‬
⃝
⃝
⃝ ⃝
⃝

42. 42
: ‫اجحات‬‫رت‬‫امل‬ ‫حل‬ ‫مجموعة‬ ‫جد‬ ( 1
2x + 5 < 7 (‫أ‬
x – 3 ≥ 6 3 (‫ب‬
: ‫االتية‬ ‫اجحات‬‫رت‬‫امل‬ ‫حلول‬ ‫مجموعة‬ ‫جد‬ (2
|x -6 | ≤ 1 (‫أ‬
|x + 1 |≤ 4 (‫ب‬
|2x – 3 | ≤ -3 (‫جـ‬
|4x + 1 | ≥ 15 (‫د‬
‫من‬ ‫لكل‬ ‫الحل‬ ‫مجموعة‬ ‫جد‬ R ‫هي‬ y ، x ‫من‬ ‫لكل‬ ‫التعويض‬ ‫مجموعة‬ ‫باختيار‬ (3
: ‫اﻵتية‬ ‫األنظمة‬
x + y = 1 ....................... 1
x2
+ 3y2
= 7 ............. 2
x y = 12 .......... 1
x2
– y2
= 32 ............. 2
x + y = 2 ........... 1
( x- 1 ) 2
+ ( y – 2 ) 2
= 5 ............. 2
x2
+ y2
= 17 ........... 1
x2
+ y2
+ 2x = 19 ........... 2
(2-3) ‫متارين‬
2-
⃝
⃝
⃝
⃝
⃝
⃝
⃝
⃝
(‫أ‬
(‫ب‬
(‫جـ‬
(‫د‬

43. 434343
‫المثلثات‬ ‫حساب‬ : ‫الثالث‬ ‫الفصل‬
‫ب‬
‫ﻧﻖ‬‫ﻧﻖ‬
‫ب‬
‫أ‬‫أ‬
‫ل‬
‫ﻧﻖ‬
‫م‬
‫ﺟـ‬
‫أ‬
‫المثلثات‬ ‫حساب‬ : ‫الثالث‬ ‫الفصل‬‫المثلثات‬ ‫حساب‬ : ‫الثالث‬ ‫الفصل‬
‫س‬
‫و‬‫و‬
‫ص‬
‫س‬‫س‬
‫أ‬
‫المثلثات‬ ‫حساب‬ : ‫الثالث‬ ‫الفصل‬‫أ‬
‫المثلثات‬ ‫حساب‬ : ‫الثالث‬ ‫الفصل‬‫المثلثات‬ ‫حساب‬ : ‫الثالث‬ ‫الفصل‬‫أ‬
‫المثلثات‬ ‫حساب‬ : ‫الثالث‬ ‫الفصل‬‫المثلثات‬ ‫حساب‬ : ‫الثالث‬ ‫الفصل‬‫المثلثات‬ ‫حساب‬ : ‫الثالث‬ ‫الفصل‬
‫ب‬
٣
٣٠
٥
٦٠
٢
١
١
٥
٤٥
٥
٤٥
٥٥
٩٠٩٠
‫ب‬‫ب‬
‫د‬ ١١١١
٤٥
١١
٢ ٢
. ‫اوية‬‫ز‬‫ال‬ [3-1]
. ‫الزوايا‬ ‫لقياس‬ ‫الدائري‬ ‫التقدير‬ [3-2]
. ‫الزوايا‬ ‫لقياس‬ ‫والدائري‬ ‫الستيني‬ ‫التقديرين‬ ‫بﻦﻴ‬ ‫العالقة‬ [3-3]
. ‫حادة‬ ‫اوية‬‫ز‬‫ل‬ ‫املثلثية‬ ‫النسب‬ [3-4]
. ‫املثلثات‬ ‫حساب‬ ‫يف‬ ‫األساسية‬ ‫العالقات‬ ‫بعض‬ [3-5]
. ‫خاصة‬ ‫لزوايا‬ ‫املثلثية‬ ‫النسب‬ [3-6]
. ‫اوية‬‫ز‬‫ل‬ ‫املثلثية‬ ‫والنقطة‬ ‫الوحدة‬ ‫دائرة‬ [3-7]
( 180ْ -⊖ ) ‫للزوايا‬ ‫املثلثية‬ ‫النسب‬ [3-8]
⊖ ∈ [0, 90ْ ) ‫حيث‬
. ‫واإلنخفاض‬ ‫اإلرتفاع‬ ‫زوايا‬ [3-9]

44. 44
‫أن‬ ‫ويتذكر‬ ‫الهندسية‬ ‫لﻸشكال‬ ‫اسة‬‫ر‬‫د‬ ‫خالل‬ ‫من‬ ‫اوية‬‫ز‬‫ال‬ ‫مفهوم‬ ‫عىل‬ ‫الطالب‬ ‫تعرف‬ ‫أن‬ ‫سبق‬
. ‫بدئهﺎﻤ‬ ‫نقطة‬ ‫يف‬ ‫مﺸرتكﻦﻴ‬ ‫شعاعﻦﻴ‬ ‫من‬ ‫تتكون‬ ‫اوية‬‫ز‬‫ال‬
‫اوية‬‫ز‬‫ال‬ ‫ويكونان‬ (B) ‫البدء‬ ‫نقطة‬ ‫يف‬ ‫مﺸرتكان‬ (3-1) ‫الﺸكل‬ ‫يف‬ BA ، B C ‫فالﺸعاعان‬
A B C
ABC ‫أو‬ ABC ‫لها‬ ‫نرمز‬ ‫التي‬
ABC = C B A ‫أن‬ ‫الحﻆ‬
BA ، B C ‫الﺸعاعان‬ ‫يسمﻰ‬
‫بدء‬ ‫ويسمﻰ‬ (‫اوية‬‫ز‬‫ال‬ ‫)ضلعي‬
(‫اوية‬‫ز‬‫ال‬ ‫)رأس‬ B ‫املﺸرتك‬ ‫الﺸعاعﻦﻴ‬
‫وحدة‬ ‫وتسمﻰ‬ Radian Measure «‫الدائري‬ ‫»التقدير‬ ‫يسمﻰ‬ ‫الزوايا‬ ‫لقياس‬ ‫نظام‬ ‫يوجد‬
: ‫يأﻲﺗ‬ ‫كﺎﻤ‬ ‫تعريفها‬ ‫وﻤﻳكن‬ ‫القطرية‬ ‫نصﻒ‬ ‫اوية‬‫ز‬‫ال‬ ‫فيه‬ ‫القياس‬
^
Angle ‫اويــــة‬‫ز‬‫ال‬ [ 3 - 1 ]
‫املثلثات‬ ‫حساب‬ : ‫الثالث‬ ‫الفصل‬
: ‫الزوايا‬ ‫لقياس‬ ‫الدائري‬ ‫التقدير‬ [3-2]
C
B
A
(3-1) ‫الﺸكل‬
^
^^
∢

45. 45
r
L
‫دائرة‬ ‫مركز‬ ‫يف‬ ‫رأسها‬ ‫وضع‬ ‫إذا‬ ‫التي‬ ‫اوية‬‫ز‬‫لل‬ ‫قياس‬ ‫وهي‬ ‫القطرية‬ ‫نصﻒ‬ ‫اوية‬‫ز‬‫ال‬
. ‫الدائرة‬ ‫تلﻚ‬ ‫قطر‬ ‫لنصﻒ‬ ٍ‫و‬‫مسا‬ ‫ﻃوله‬ ‫قوس‬ ‫وقابلها‬
‫يساوي‬ AO B ‫املركزية‬ ‫اوية‬‫ز‬‫لل‬ ‫املقابل‬ ‫القوس‬ ‫ﻃول‬ ‫أن‬ ‫فرضنا‬ ‫إذا‬ (3-2)‫الﺸكل‬ ‫ففي‬
m A O B ‫فﺈن‬ L=r ‫وكان‬ ‫ﻃول‬ ‫وحدة‬ (r)= ‫الدائرة‬ ‫قطر‬ ‫نصﻒ‬ ، ‫ﻃول‬ ‫وحدة‬ (L)
‫فﺈن‬ (3-3) ‫الﺸكل‬ ‫يف‬ ‫كﺎﻤ‬ L = 2 r ‫كان‬ ‫وإذا‬ ‫قطرية‬ ‫نصﻒ‬ ‫اوية‬‫ز‬ 1= ‫الدائري‬ ‫بالتقدير‬
. ‫قطريتﻦﻴ‬ ‫نصﻒ‬ ‫اويتﻦﻴ‬‫ز‬ = ‫الدائري‬ ‫بالتقدير‬ m A O B
(3-3) ‫الﺸكل‬ (3-2) ‫الﺸكل‬
= ‫الدائري‬ ‫بالتقدير‬ ً‫ا‬‫ر‬‫مقد‬ ‫املركزية‬ ‫اوية‬‫ز‬‫ال‬ ‫قياس‬ ∴
⊖ =
B
A
L
rO
r
‫لها‬ ‫املقابل‬ ‫القوس‬ ‫ﻃول‬
‫الدائرة‬ ‫قطر‬ ‫نصﻒ‬
: ( 3-1 ) ‫تعريﻒ‬
L
B
r
r
O
A

46. 46
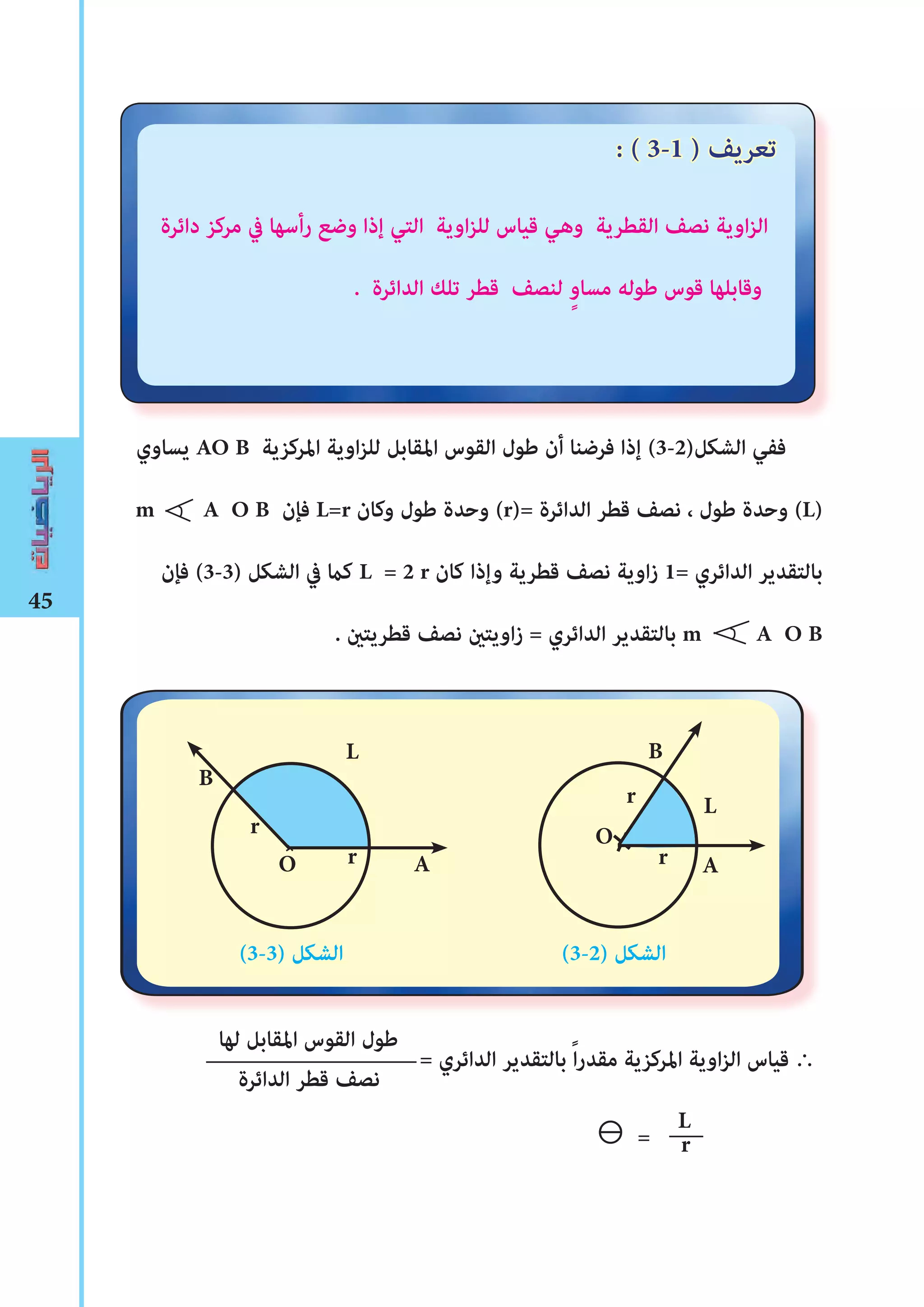
: ‫الزوايا‬ ‫لقياس‬ ‫والدائري‬ ‫الستيني‬ ‫التقديرين‬ ‫بﻦﻴ‬ ‫العالقة‬ [3-3]
: ‫فﺈنه‬ ‫املتوسطة‬ ‫املرحلة‬ ‫يف‬ ‫نعلم‬ ‫وكﺎﻤ‬
‫قوس‬ ‫كل‬ ، ً‫ا‬‫متساوي‬ ً‫ا‬‫قوس‬ 360 ‫عىل‬ ‫نحصل‬ ‫فﺈننا‬ ً‫ا‬‫متساوي‬ ً‫ﺎﻤ‬‫قس‬ 360 ‫إﱃ‬ ‫دائرة‬ ‫قسمنا‬ ‫إذا‬
‫الستيني‬ ‫القياس‬ ‫يف‬ ‫درجة‬ ‫يسمﻰ‬ ‫قياسها‬ ‫الدائرة‬ ‫هذه‬ ‫يف‬ ‫مركزية‬ ‫اوية‬‫ز‬ ‫يقابل‬ ‫منها‬
: ‫إن‬ ‫كﺎﻤ‬ ، ( 1ْ ) ُ‫ه‬‫ل‬ ‫ويرمز‬ Degree Measure
1ْ = ‫دقيقة‬ 60 = 60َ
1َ = ‫ثانية‬ 60 = 60
2π r = ‫الدائرة‬ ‫محيﻂ‬ ‫أن‬ ً‫ا‬‫سابق‬ ‫ذكرنا‬
⊖ = = ‫أن‬ ‫ومبا‬
360 ْ = ‫قطرية‬ ‫نصﻒ‬ ‫اوية‬‫ز‬ 2π ∴
180ْ = ‫قطرية‬ ‫نصﻒ‬ ‫اوية‬‫ز‬ π ⇐
= ‫قطرية‬ ‫نصﻒ‬ ‫اوية‬‫ز‬ 1 ∴
. ‫قطرية‬ ‫نصﻒ‬ ‫اوية‬‫ز‬ 0 .0 1745= ‫قطرية‬ ‫نصﻒ‬ ‫اوية‬‫ز‬ = 1ْ ∴
: ‫عامة‬ ‫وبصورة‬
‫الدائري‬ ‫التقدير‬ ‫من‬ ‫اوية‬‫ز‬‫ال‬ ‫قياس‬ ‫لتحويل‬ ‫اعاله‬ ‫العالقة‬ ‫تستخدم‬ =
‫اوية‬‫ز‬‫ال‬ ‫قياس‬ ⊖ ‫الستيني‬ ‫بالنظام‬ ‫اوية‬‫ز‬‫ال‬ ‫قياس‬ D ‫يكون‬ ‫حيث‬ ‫وبالعكس‬ ‫الستيني‬ ‫إﱃ‬
. ‫الدائري‬ ‫بالنظام‬
L
r
2π r
r
180ْ
π
180ْ
π
ً
180
π
Dْ
⊖
°

47. 47
1 ‫مثال‬
2 ‫مثال‬
‫ول‬ّ‫ح‬
‫الدائري‬ ‫التقدير‬ ‫إﱃ‬ 40٥
(‫أ‬
‫الدائري‬ ‫التقدير‬ ‫إﱃ‬ 75٥
(‫ب‬
‫الستيني‬ ‫التقدير‬ ‫إﱃ‬ 2.6 (‫جـ‬
‫الستيني‬ ‫التقدير‬ ‫إﱃ‬ (‫د‬
/ ‫الحــل‬
= ⇒ = ⇒ ⊖ = (‫أ‬
. ‫قطرية‬ ‫النصﻒ‬ ‫الزوايا‬ ‫من‬
= ⇒ = ⇒ ⊖ = (‫ب‬
‫قطرية‬ ‫النصﻒ‬ ‫الزوايا‬ ‫من‬
= ⇒ = ⇒ D = 180ْ × 2.6 = 468 ( ‫جـ‬
= ⇒ = ⇒ Dْ = 180 × = 45ْ (‫د‬
‫نصﻒ‬ ‫ﻃول‬ ‫كان‬ ‫إذا‬ ‫تقابله‬ ‫الذي‬ ‫القوس‬ ‫ﻃول‬ ‫فﺎﻤ‬ 60ْ ‫قياسها‬ ‫مركزية‬ ‫اوية‬‫ز‬
‫؟‬ ‫سم‬ 9 ‫دائرتها‬ ‫قطر‬
/ ‫الحــل‬
= ⇒ = ⇒ ⊖ = ‫قطرية‬ ‫النصﻒ‬ ‫الزوايا‬ ‫من‬
π
180
1
4
⊖
D
π
180
⊖
40
2π
9
π
180
⊖
D
π
180
⊖
75
5π
12
π
180ْ
π
180
⊖
Dْ
π
180ْ
π
180
2.6π
Dْ
Dْ
1
4
π
1
4
π
180
π
180
π
3
⊖
Dْ
⊖
Dْ
⊖
60ْ
π
π
°°°
° ° °
° °
° °
°
°
°
°

48. 48
= ‫الدائري‬ ‫بالتقدير‬ ‫اوية‬‫ز‬‫ال‬ ‫قياس‬ ∵
= ⇒ =
‫القوس‬ ‫ﻃول‬ ‫سم‬ L = 3 π = 3 × 3.142 = 9.426
‫سم‬ 20 ‫دائرتها‬ ‫قطر‬ ‫نصﻒ‬ ‫وﻃول‬ ‫سم‬ 22 ‫قوسها‬ ‫ﻃول‬ ‫مركزية‬ ‫اوية‬‫ز‬
‫؟‬ ‫الستيني‬ ‫قياسها‬ ‫مقدار‬ ‫فﺎﻤ‬
= ‫بالدائري‬ ‫املركزية‬ ‫اوية‬‫ز‬‫ال‬ ‫قياس‬ / ‫الحــل‬
‫قطرية‬ ‫نصﻒ‬ ‫اوية‬‫ز‬ =
∵ = ⇒ =
∴ D = × = 63ْ ‫الستيني‬ ‫بالتقدير‬ ‫القياس‬
‫نصﻒ‬ ‫فﺎﻤ‬ ‫5سم‬ ‫يساوي‬ 35ْ ‫مقدارها‬ ‫مركزية‬ ‫اوية‬‫ز‬‫ل‬ ‫املقابل‬ ‫القوس‬ ‫ﻃول‬
‫؟‬ ‫دائرته‬ ‫قطر‬
/ ‫الحــل‬
= ⇒ = ⇒ ⊖ = ‫قطرية‬ ‫نصﻒ‬ ‫زوايا‬
⊖ = ⇒ = ‫ثم‬
∴r = = 7.18 cm ‫القطر‬ ‫نصﻒ‬ ‫ﻃول‬
L
r
π
180ْ
22
20
D
180
π
L
r
π
3
3 ‫مثال‬
L
r
22
20
π
180ْ
22
20
4 ‫مثال‬
L
r
5
r
⊖
Dْ
π
180ْ
⊖
Dْ
π
180ْ
⊖
35ْ
35
180ْ
π
35
180ْ
π
180 × 5
35π
L
9
π
3
°°
°

49. 49
‫اﻵتية‬ ‫الزوايا‬ ‫قياس‬ ‫من‬ ‫كل‬ ‫الدائري‬ ‫التقدير‬ ‫اﱃ‬ ‫حول‬ (1
30 ٥
، 120 ٥
، 15 ٥
، 300 ٥
‫الستيني‬ ‫التقدير‬ ‫اﱃ‬ ‫اﻵتية‬ ‫قطرية‬ ‫النصﻒ‬ ‫الزوايا‬ ‫من‬ ‫كال‬ ‫حول‬ (2
، ، ،
‫تقابل‬ ‫قطرية‬ ‫النصﻒ‬ ‫الزوايا‬ ‫من‬ ‫دائرة‬ ‫يف‬ ‫مركزية‬ ‫اوية‬‫ز‬ ‫قياس‬ (3)
‫سم‬ 30 / ‫ج‬ . ‫الدائرة‬ ‫تلﻚ‬ ‫قطر‬ ‫نصﻒ‬ ‫جد‬ ‫سم‬ 25 ‫ﻃوله‬ ‫قوسا‬
‫قطرها‬ ‫نصﻒ‬ ‫دائرة‬ ‫يف‬ 135٥
‫قياسها‬ ‫مركزية‬ ‫اوية‬‫ز‬‫ل‬ ‫املقابل‬ ‫القوس‬ ‫ﻃول‬ ‫ما‬ (4
‫سم‬ 18.857 /‫ج‬ ‫سم؟‬ 8
. ‫سم‬ 6 ‫دائرتها‬ ‫قطر‬ ‫نصﻒ‬ ‫وﻃول‬ ‫سم‬ 9.42 ‫قوسها‬ ‫ﻃول‬ ‫مركزية‬ ‫اوية‬‫ز‬ ( 5
( π = 3.14 ) ‫؟‬ ‫الستيني‬ ‫بالتقدير‬ ‫مقدارها‬ ‫فﺎﻤ‬
90 / ‫ج‬
5
3 π
6
5 π
3
π
3
1
6
5
(3-1) ‫متارين‬
°

50. 50
: B ‫يف‬ ‫اوية‬‫ز‬‫ال‬ ‫القائم‬ ∆ A B C
‫وتكتب‬ (⊖) ‫الحادة‬ ‫اوية‬‫ز‬‫ال‬ (Sine )‫جيب‬
Sin ⊖ = =
‫وتكتب‬Cos ‫له‬ ‫ويرمز‬ (⊖) ‫الحادة‬ ‫اوية‬‫ز‬‫ال‬ (Cosine ) ‫متام‬ ‫جيب‬
Cos⊖ = =
‫وتكتب‬ (⊖ ) ‫الحادة‬ ‫اوية‬‫ز‬‫ال‬ ( Tangent) ‫ﻇل‬
tan⊖ = =
‫حادة‬ ‫اوية‬‫ز‬‫ل‬ ‫املثلثية‬ ‫النسب‬ ‫من‬
sin⊖ , cos⊖ ∈ [ -1 , 1 ]
sin 0 = 0 , sin 90ْ = 1
cos 0 = 1 , cos 90ْ = 0
tan 0 = 0 , tan 90ْ ‫معرفة‬ ‫ﻏري‬
‫الوتر‬
‫املقابل‬ AB
AC
B C
AC
‫املجاور‬
‫املقابل‬ A B
B C
: ‫حادة‬ ‫لزواية‬ ‫املثلثية‬ ‫النسب‬ [3-4]
: ( 3-2 ) ‫تعريﻒ‬
‫الوتر‬
‫املجاور‬
‫وتكتب‬ (
‫وتكتب‬Cos ‫له‬ ‫ويرمز‬ (⊖) ‫الحادة‬ ‫اوية‬‫ز‬‫ال‬ (
OPPOSITEHypotenuse
A
AdgacentC B
: ‫مالحظة‬
(3-4) ‫الﺸكل‬
⊖

51. 51
: ⊖ ‫الحادة‬ ‫اوية‬‫ز‬‫وال‬ B‫يف‬ ‫اوية‬‫ز‬‫ال‬ ‫قائم‬ ً‫ا‬‫مثلث‬ ‫ﻤﻳثل‬ (3-4) ‫الﺸكل‬
: ‫أن‬ ‫نجد‬ A B C ‫املثلث‬ ‫عىل‬ ‫فيثاﻏورس‬ ‫مﱪهنة‬ ‫بتطبيق‬
( A C )2
‫عىل‬ ‫الحدود‬ ‫كل‬ ‫بقسمة‬
( )2
+ ( )2
=1
( )2
+ ( )2
= 1
sin2
⊖ + cos2
⊖ = 1
‫ينتﺞ‬ (AC) ‫عىل‬ ‫بالقسمة‬ tan ⊖ = ‫كذلﻚ‬
∴tan ⊖ =
ABC ‫املثلث‬ ‫يف‬ cos C = ‫أن‬ ‫علمﺖ‬ ‫اذا‬
tanC ، sin A ، cos A . ‫جد‬ B ‫يف‬ ‫اوية‬‫ز‬‫ال‬ ‫القائم‬
B ‫يف‬ ‫اوية‬‫ز‬‫ال‬ ‫القائم‬ A B C ‫املثلث‬ ‫نرسم‬ /‫الحــل‬
∴ cos C = , BC = 5K , AC= 13K, K ‫ثابﺖ‬
( AB)2
+ ( BC)2
= (AC)2
AB
A C
5
13
5
13
: ‫املثلثات‬ ‫حساب‬ ‫يف‬ ‫األساسية‬ ‫العالقات‬ ‫بعض‬ [ 3-5 ]
B C
A C
5 ‫مثال‬
∴
5 K
C
13K
A
B
(3-5) ‫الﺸكل‬
12 K
‫الوتر‬
‫املقابل‬
‫الوتر‬
‫املجاور‬
sin⊖
cos⊖
AB
B C

52. 52
: ‫فيثاﻏورس‬ ‫مﱪهنة‬ ‫باستخدام‬
(A C )2
= (A B )2
+ ( B C )2
(13K)2
= (A B )2
+ ( 5 K )2
(A B)2
= 144 K2
∴AB = 12 K
tan C = =
sinA = =
cos A = =
. C ‫يف‬ ‫اوية‬‫ز‬‫ال‬ ‫القائم‬AB C ‫املثلث‬ ‫يف‬ tan A = ‫ان‬ ‫علمﺖ‬ ‫اذا‬
. cosB , tinA ‫جد‬
C ‫يف‬ ‫اوية‬‫ز‬‫ال‬ ‫القائم‬ ABC ‫املثلث‬ ‫نرسم‬ / ‫الحــل‬
tanA = ⇒ B C = 7 K , A C = 24 K
(A B)2
= (A C)+2
(B C)2
(AB)2
= (24K)2
+ ( 7 K)2
AB = 25 K
12 K
5 K
12
5
5 K
13K
5
13
12 K
13 K
12
13
6 ‫مثال‬
(A B)
(AB)
AB = 25 K
B
25 K
24 K
7K
C
(3-6) ‫الﺸكل‬
7
24
7
24
A

53. 53
sinA = =
cos B = =
‫جيب‬ ‫فان‬ ‫متتامتان‬ ‫اويتان‬‫ز‬ ‫أنهﺎﻤ‬ ‫اي‬ ( 90ْ ) ‫يساوي‬ ‫اويتﻦﻴ‬‫ز‬ ‫مجموع‬ ‫كان‬ ‫اذا‬
.(6) ‫مثال‬ ‫الحﻆ‬ ‫وبالعكس‬ ‫األخرى‬ ‫متام‬ ‫جيب‬ ‫يساوي‬ ‫احدهﺎﻤ‬
30ْ ، 45ْ ، 60 ْ
: 45 ْ ‫قياسها‬ ‫اوية‬‫ز‬ (1)
AC= 2 K ‫نجد‬ ‫فيثاﻏورس‬ ‫وباستخدام‬ AB = K , BC = K : ‫ان‬ ‫نفرض‬
sin45ْ = =
cos 45ْ = =
tan 45ْ = = 1
A C
B C
2
1
AB
BC
AB
AC
: ‫مالحظة‬
: ‫الخاصة‬ ‫للزوايا‬ ‫املثلثية‬ ‫النسب‬ [ 3 - 6 ]
sin45ْ = =
cos 45ْ = =
tan 45ْ = = 1
45ْ
90ْ
K
k B
(3-7) ‫الﺸكل‬
7 K
25 K
7
25
7 K
25 K
7
25
A
45ْ
2 K
C
2
1

54. 54
٣
٤
٣
٤
90ْ 60ْ 45ْ 30ْ
1 0
0 1
‫معرف‬ ‫ﻏري‬ 3 1 0
‫ة‬‫ي‬‫ث‬‫ل‬‫ث‬‫مل‬‫ا‬ ‫ب‬‫س‬‫ن‬‫ل‬‫ا‬
‫ة‬‫ص‬‫ا‬‫خ‬‫ل‬‫ا‬ ‫ا‬‫ي‬‫ا‬‫و‬‫ز‬‫ل‬‫ا‬
2
1
2
1
2
3
2
1
2
1
2
3
3
1
1
2
BD
AB
AD
AB
BD
AD
3
2
3
1
A
(3-8) ‫الﺸكل‬
2K
C
2K
K KDB
60 ْ
AD
AB
3
2
BD
AB
1
2
AD
BD
3
3 K
sin
cos
tan
0 ْ
30 ْ
: 30٥
‫قياسها‬ ‫اوية‬‫ز‬ (2)
sin30ْ = =
cos 30ْ = =
tan 30ْ
= =
: 60ْ ‫قياسها‬ ‫اوية‬‫ز‬ (3)
sin60ْ = =
cos 60ْ = =
tan 60ْ
= =
: ‫اﻵﻲﺗ‬ ‫بالجدول‬ ‫الخاصة‬ ‫املثلثيةللزوايا‬ ‫النسب‬ ‫تلخيﺺ‬ ‫وﻤﻳكن‬

55. 55
:‫ﻗﻴﻤﺔ‬ ‫ﺟﺪ‬
tan2
30ْ + 2 sin 60ْ + 3tan 45ْ + cos2
30ْ - tan 60ْ
/ ‫اﻟﺤــﻞ‬
( )2
+ 2 × +3×1+ ( )2
-
× + + 3 + -
+ 3 + = 1 + 3 = 4
4cos 30ْ cos 45ْ sin 30ْ sin 60ْ sin 45ْ : ‫اﳌﻘﺪار‬ ‫ﻗﻴﻤﺔ‬ ‫ﺟﺪ‬
/ ‫اﻟﺤــﻞ‬
4 × × × × × =
sin 60ْ cos 30ْ + cos 60ْ sin 30ْ : ‫اﳌﻘﺪار‬ ‫ﻗﻴﻤﺔ‬ ‫ﺟﺪ‬
/ ‫اﻟﺤــﻞ‬
× + × = + = 1
3
4
7 ‫مثال‬
8 ‫مثال‬
9 ‫مثال‬
3
4 3
1 3
2
3
2
3
3
2 2
1 1
2
3
2 2
1 3
4
3
2
3
2
1
2
1
2
3
4
1
4
‫املقدار‬ =
3
4
1
3
3 3
4
3=
1
4
3
4
=
‫املقدار‬ =
‫املقدار‬ =

56. 56
‫قطرها‬ ‫ونصﻒ‬ ‫األصل‬ ‫نقطة‬ ‫مركزها‬ ‫دائرة‬ ‫هي‬Unit Circle : ‫الوحدة‬ ‫دائرة‬
. ‫واحدة‬ ‫ﻃول‬ ‫وحدة‬ ‫يساوي‬
AO B ‫لتكن‬ O B ‫النهاﻲﺋ‬ ‫وضلعها‬ O A ‫االبتداﻲﺋ‬ ‫ضلعها‬ ‫أن‬ ‫حيث‬ (3-9) ‫الﺸكل‬ ‫يف‬
. ‫الوحدة‬ ‫دائرة‬ ‫مع‬ OB‫النهاﻲﺋ‬ ‫الضلع‬ ‫تقاﻃع‬ ‫نقطة‬ B ,‫القياﳼ‬ ‫الوضع‬ ‫يف‬ ‫موجهة‬ ‫اوية‬‫ز‬
B = ( x , y ) ‫أن‬ ‫نفرض‬
sin ⊖ = ‫أن‬ ‫تعلم‬
⇒ y = sin ⊖
‫املثلثية‬ ‫بالنقطة‬ ‫تدعﻰ‬ ‫النقطة‬ ‫هذه‬ B = ( x , y) = ( cos ⊖ , sin ⊖ )
Trigonometric Point
y
1
: ‫اوية‬‫ز‬‫لل‬ ‫املثلثية‬ ‫والنقطة‬ ‫الوحدة‬ ‫دائرة‬ [3-7]
: ( 3-3 ) ‫تعريﻒ‬
X
Y
y
x
B ( x , y )
١
( 3 - 9 ) ‫الﺸكل‬
o A
⊖
x
1cos ⊖ = ⇒ x = cos ⊖ ‫أن‬ ‫ثم‬

57. 57
‫ﻤﻳكن‬ ‫عليه‬ ‫املوجبة‬ ‫الحادة‬ ‫للزوايا‬ ‫املثلثية‬ ‫النسب‬ ‫تحوي‬ ‫الرياضية‬ ‫الجداول‬ ‫أن‬ ‫نعلم‬
‫هذا‬ ‫استنا‬‫ر‬‫د‬ ‫وسنقﴫ‬ ‫ابع‬‫ر‬‫ال‬ ‫أو‬ ‫الثالث‬ ‫أو‬ ‫الثاين‬ ‫الربع‬ ‫يف‬ ‫تقع‬ ‫اوية‬‫ز‬ ‫الية‬ ‫املثلثية‬ ‫النسب‬ ‫إيجاد‬
‫املستوي‬ ‫عىل‬ ‫واإلنعكاس‬ ‫الوحدة‬ ‫دائرة‬ ‫باستخدام‬ . ‫والحادة‬ ‫املنفرجة‬ ‫الزوايا‬ ‫عىل‬ ‫العام‬
: ‫ان‬ ‫نجد‬ ‫حيث‬ ‫الثاين‬ ‫الربع‬ ‫يف‬ ‫تقع‬ ‫التي‬ ‫للزوايا‬ ‫املثلثية‬ ‫النسب‬ ‫ايجاد‬ ‫ﻤﻳكن‬
sin ( 180ْ - ⊖ ) = sin ⊖ , ⊖ ∈ [ 0 , 90ْ )
cos ( 180ْ - ⊖ ) = - cos ⊖
tan ( 180ْ - ⊖ ) = - tan ⊖
cos 120ْ ، sin 135 ْ ، tan150 ْ ‫قيمة‬ ‫جد‬
/ ‫الحــل‬
cos 120ْ = cos ( 180ْ - 60ْ ) = - cos 60ْ =
sin 135ْ = sin ( 180ْ - 45ْ ) = sin 45ْ =
tan 150ْ = tan ( 180ْ - 30ْ ) = - tan 30ْ =
-1
2
( 180 ْ _⊖ ) ‫اوية‬‫ز‬‫لل‬ ‫املثلثية‬ ‫النسب‬ ‫إيجاد‬ [3-8 ]
⊖ ∈ [0 , 90ْ ) ‫حيث‬
10 ‫مثال‬
1
2
-1
3

58. 58
٥
1
2
(3-2) ‫متارين‬
3
5
٥
٥
: ‫مﺎﻤيأﻲﺗ‬ ‫لكل‬ ‫العددية‬ ‫القيمة‬ ‫جد‬ (1
( tan 30ْ - tan 60ْ ) ( 2 tan 60ْ tan 45ْ ) ( ‫أ‬
( sin 30ْ + cos 60ْ ) (cos 60ْ - sin 60ْ ) (‫ب‬
3cos 30ْ tan 60ْ - 2 tan 45ْ - sin 60ْ ( ‫جـ‬
cos 2
45ْ sin 60 ْ tan 60ْ tan2
45 ْ cos2
30ْ ( ‫د‬
‫مثلث‬ ‫يف‬ ‫حادة‬ ‫ﺯﺍﻭﻳﺔ‬ ⊖ ‫أن‬ ‫حيث‬cos ⊖ , tan ⊖ ‫فجد‬ sin ⊖ = ‫كان‬ ‫اذا‬ (2
.‫اوية‬‫ز‬‫ال‬ ‫قائم‬
: ‫املرتبتﻦﻴ‬ ‫املجموعتﻦﻴ‬ ‫أن‬ ‫عىل‬ ‫برهن‬ (3
‫متناسبتان‬ { sin 2
30 , sin 2
45ْ , sin 2
60 , sin 2
90ْ } ، { 1 , 2 , 3 , 4 }
: ‫منها‬ ‫لكل‬ ‫املثلثية‬ ‫النقطة‬ ‫جد‬ ‫ثم‬ ‫يأﻲﺗ‬ ‫مﺎﻤ‬ ‫لكل‬ ‫العددية‬ ‫القيمة‬ ‫جد‬ (4
cos150ْ , sin 150ْ ( ‫أ‬
cos 135ْ , tan135ْ (‫ب‬
tan 120 , sin 120ْ (‫جـ‬

59. 59
m B = 60 AC = 4 cm ‫فيه‬ C ‫يف‬ ‫اوية‬‫ز‬‫ال‬ ‫قائم‬ ‫مثلث‬ A B C (5
. ‫مساحته‬ ‫جد‬
‫االعىل‬ ‫وﻃرفه‬ ‫مستوية‬ ‫أفقية‬ ‫أرض‬ ‫عىل‬ ‫األسفل‬ ‫بطرفه‬ ‫مرتكز‬ ‫مرت‬ 10 ‫ﻃوله‬ ‫سلم‬ (6
‫األعىل‬ ‫ﻃرفه‬ ‫بعد‬ ‫فﺎﻤ‬ 30ْ ‫واألرض‬ ‫السلم‬ ‫بﻦﻴ‬ ‫اوية‬‫ز‬‫ال‬ ‫كانﺖ‬ ‫فاذا‬ ‫شاقوﱄ‬ ‫حائﻂ‬ ‫عىل‬
( 3 = 1.7) ‫؟‬ ‫الحائﻂ‬ ‫عن‬ ‫األسفل‬ ‫ﻃرفه‬ ‫بعد‬ ‫وما‬ ‫؟‬ ‫األرض‬ ‫عن‬
. tan ⊖, L ‫قيمة‬ ‫جد‬ ،⊖ ‫الحادة‬ ‫اوية‬‫ز‬‫لل‬ ‫مثلثية‬ ‫نقطة‬ ( , L ) (7
∀
3
2
٥

60. 60
‫فيها‬ ‫اها‬‫ر‬‫ن‬ ‫التي‬ ‫الزوايا‬ ‫قياس‬ ‫من‬ ‫نتمكن‬ ‫عندما‬ ‫واألبعاد‬ ‫االرتفاعات‬ ‫حساب‬ ‫من‬ ‫نتمكن‬
‫الحاصلة‬ ‫اوية‬‫ز‬‫ال‬ ‫فان‬ A ‫أفق‬ ‫فوق‬ ‫تقع‬ ‫التي‬ C ‫نقطة‬ ‫اﱃ‬ ‫ونظر‬ A‫نقطة‬ ‫يف‬ ‫اصد‬‫ر‬ ‫فاذاوقﻒ‬
C ‫ارتفاع‬ ‫اوية‬‫ز‬) ‫تدعﻰ‬ A ‫أفق‬ ‫وبﻦﻴ‬ C ‫النقطة‬ ‫اﱃ‬ ‫اصد‬‫ر‬‫ال‬ ‫عﻦﻴ‬ ‫من‬ ‫الواصل‬ ‫املستقيم‬ ‫بﻦﻴ‬
‫يف‬ ‫اصد‬‫ر‬‫ال‬ ‫عﻦﻴ‬ ‫كانﺖ‬ ‫اذا‬ ‫أما‬ ( 3 - 10) ‫الﺸكل‬ ‫يف‬ CAB ‫اوية‬‫ز‬‫ال‬ ‫مثل‬ (A ‫اﱃ‬ ‫بالنسبة‬
‫اصد‬‫ر‬‫ال‬ ‫عﻦﻴ‬ ‫من‬ ‫الواصل‬ ‫املستقيم‬ ‫بﻦﻴ‬ ‫الكائنة‬ ‫اوية‬‫ز‬‫ال‬ ‫فان‬ ،C ‫أفق‬ ‫تحﺖ‬ ‫التي‬ A‫اﱃ‬ ‫ونظر‬ C
C ‫أفق‬ ‫وبﻦﻴ‬ A ‫النقطة‬ ‫اﱃ‬
( 3 - 10)‫الﺸكل‬ ‫يف‬ A C X ‫اوية‬‫ز‬‫ال‬ ‫مثل‬ (C ‫اﱃ‬ ‫بالنسبة‬ A ‫انخفاض‬ ‫اوية‬‫ز‬ ) ‫تدعﻰ‬
‫مع‬ ‫الخيﻂ‬ ‫يصنعها‬ ‫التي‬ ‫اوية‬‫ز‬‫ال‬ ‫كانﺖ‬ ‫فاذا‬ ‫03م‬ ‫خيطها‬ ‫ﻃول‬ ‫ورقية‬ ‫ﻃائرة‬
. ‫االرض‬ ‫عن‬ ‫الطائرة‬ ‫ارتفاع‬ ‫جد‬ 60 ‫هي‬ ( ‫االفق‬ ) ‫االرض‬
L = ‫االرض‬ ‫عن‬ ‫الطائرة‬ ‫ارتفاع‬ ‫ان‬ ‫نفرض‬ ( 3 - 11) ‫الﺸكل‬ ‫يف‬ / ‫الحــل‬
‫الطول‬ ‫وحدات‬ ‫من‬
sin 60٥
= =
L= 15 3 ‫االرتفاع‬ ‫مرت‬
: ‫واالنخفاض‬ ‫األرتفاع‬ ‫اويا‬‫ز‬ [ 3 - 9 ]
(3-10) ‫الﺸكل‬
‫انخفاض‬ ‫اوية‬‫ز‬
C
BA
11 ‫مثال‬
L
30
3
2sin 60
L= 15 3
٥
60
‫م‬ 30
C
B
(3-11) ‫الﺸكل‬
⇐
A
L
30L
X
٥
‫ارتفاع‬ ‫اوية‬‫ز‬

61. 61
‫عن‬ ‫مرت‬ 8 ‫تبعد‬ ‫االرض‬ ‫عىل‬ ‫نقطة‬ ‫من‬ ‫مﺌذنة‬ ‫قمة‬ ‫ارتفاع‬ ‫اوية‬‫ز‬ ‫ان‬ ‫اصد‬‫ر‬ ‫وجد‬
‫املﺌذنة؟‬ ‫ارتفاع‬ ‫فﺎﻤ‬ 45 ‫تساوي‬ ‫قاعدتها‬
B ‫يف‬ ‫اوية‬‫ز‬‫ال‬ ‫قائم‬ ABC / ‫الحــل‬
tan 45 =
1 =
‫املﺌذنة‬ ‫ارتفاع‬ ‫مرت‬ 8 = AB ∴
‫نقطة‬ ‫انخفاض‬ ‫اوية‬‫ز‬ ‫قياس‬ ‫أن‬ ‫قمته‬ ‫من‬ ‫اصد‬‫ر‬ ‫وجد‬ ‫مرت‬ 2350 ‫ارتفاعه‬ ‫جبل‬
‫؟‬ ‫اصد‬‫ر‬‫وال‬ ‫النقطة‬ ‫بﻦﻴ‬ ‫البعد‬ ‫هو‬ ‫فﺎﻤ‬ 30 ‫االرض‬ ‫عىل‬
‫االنخفاض‬ ‫اوية‬‫ز‬ ‫قياس‬ = ‫االرتفاع‬ ‫اوية‬‫ز‬ ‫قياس‬ / ‫الحــل‬
: B ‫يف‬ ‫اوية‬‫ز‬‫ال‬ ‫قائم‬ ABC
Sin 30 =
=
. ‫اصد‬‫ر‬‫وال‬ ‫النقطة‬ ‫بﻦﻴ‬ ‫البعد‬ ‫مرت‬ 4700 = AC ∴
12 ‫مثال‬
‫املقابل‬
‫املجاور‬
A B
8
BC
(3-12) ‫الﺸكل‬
45
‫م‬ 8
13 ‫مثال‬
AB
AC
1
2
2350
AC
30
30
‫0532م‬
(3-13) ‫الﺸكل‬
A
B
A
C
٥
٥
٥
٥
٥
٥
٥

62. 62
‫استقامة‬ ‫عىل‬ ‫الﱪج‬ ‫قاعدة‬ ‫مع‬ ‫تقعان‬ ‫شجرتﻦﻴ‬ ‫وأبﴫ‬ ‫برج‬ ‫أعىل‬ ‫يف‬ ‫شخﺺ‬ ‫وقﻒ‬ (1
‫انخفاض‬ ‫اوية‬‫ز‬‫و‬ 60٥
‫األوﱃ‬ ‫الﺸجرة‬ ‫قاعدة‬ ‫انخفاض‬ ‫اوية‬‫ز‬ ‫فكانﺖ‬ ، ‫واحدة‬
.‫الﺸجرتﻦﻴ‬ ‫بﻦﻴ‬ ‫املسافة‬ ‫جد‬ 45٥
‫الثانية‬ ‫الﺸجرة‬ ‫قاعدة‬
. ‫ا‬‫رت‬‫م‬ 30 ‫الﱪج‬ ‫ارتفاع‬ ‫أن‬ ‫العلم‬ ‫مع‬
8m /‫ج‬
‫فﺎﻤ‬ 30 ٥
‫قمتها‬ ‫ارتفاع‬ ‫اوية‬‫ز‬ ‫أن‬ ‫وجد‬ ‫ا‬‫رت‬‫م‬ 50 ‫مﺌذنة‬ ‫قاعدة‬ ‫عن‬ ‫تبعد‬ ‫نقطة‬ ‫من‬ (2
. ‫املﺌذنة‬ ‫ارتفاع‬
25m /‫ج‬
‫ومربوط‬ ‫أفقية‬ ‫أرض‬ ‫عىل‬ (‫)عموديا‬ ‫شاقوليا‬ ‫مثبﺖ‬ ‫أمتار‬ 6 ‫كهرباءﻃوله‬ ‫3(عمود‬
‫يصنعها‬ ‫التي‬ ‫اوية‬‫ز‬‫ال‬ ‫قياس‬ ‫وكان‬ ‫األرض‬ ‫سطﺢ‬ ‫عىل‬ ‫ومثبﺖ‬ ‫العليا‬ ‫نهايته‬ ‫يف‬ ‫بسلﻚ‬
. ‫السلﻚ‬ ‫ﻃول‬ ‫فﺎﻤ‬ 60٥
‫األرض‬ ‫سطﺢ‬ ‫مع‬ ‫السلﻚ‬
6.92m /‫ج‬
‫افق‬ ‫مستوى‬ ‫يف‬ ‫اصد‬‫ر‬‫ال‬ ‫سار‬ ‫وملا‬ 45 ٥
‫هي‬ ‫مثبﺖ‬ ‫منطاد‬ ‫ارتفاع‬ ‫اوية‬‫ز‬ ‫اصد‬‫ر‬ ‫وجد‬ (4
‫ارتفاع‬ ‫جد‬ ،60 ٥
‫هي‬ ‫االرتفاع‬ ‫اوية‬‫ز‬ ‫ان‬ ‫شاهد‬ m 1000 ‫مسافة‬ ‫املنطاد‬ ‫نحو‬
. ‫املنطاد‬
‫ج/5632م‬
(3-3) ‫متارين‬

63. 63
‫ل‬‫ص‬
١
‫ص‬-٢
‫ص‬ ١
‫ص‬ - ‫ص‬
‫س‬ - ‫س‬ ١
‫س‬ - ‫س‬
‫م‬
‫س‬‫ب‬
‫ص‬
63
‫ص‬
٢
‫ل‬ ١
‫ل‬‫ل‬
٥
٤٥
‫س‬
٥
١٥٠
١
‫ص‬-٢
‫ص‬ ١
‫ص‬ - ‫ص‬
١
‫س‬ -٢
‫س‬ ١
‫س‬ - ‫س‬
. ‫االحداﻲﺛ‬ ‫املستوي‬ ‫يف‬ ‫نقاط‬ ‫مجموعة‬ ‫]1-4[معادلة‬
. ‫املستقيم‬ ‫معادلة‬ [4-2]
. ‫املستقيم‬ ‫ميل‬ [4-3]
. ‫معادلته‬ ‫من‬ ‫املستقيم‬ ‫ميل‬ ‫استنتاج‬ [4-4]
. ‫متوازيﻦﻴ‬ ‫مستقيمﻦﻴ‬ ‫ميﲇ‬ ‫بﻦﻴ‬ ‫العالقة‬ [4-5]
. ‫متعامدين‬ ‫مستقيمﻦﻴ‬ ‫ميﲇ‬ ‫بﻦﻴ‬ ‫العالقة‬ [4-6]
‫أ‬
‫س‬
١
‫س‬ -٢
‫س‬
‫االحداثية‬ ‫الهندسة‬ : ‫ابع‬‫ر‬‫ال‬ ‫الفصل‬

64. 64
Analytic Geometry
‫فاذا‬ ‫مستوي‬ ‫يف‬ ‫نقطة‬ ‫يعﻦﻴ‬ ‫الحقيقية‬ ‫األعداد‬ ‫من‬ (x , y ) ‫مرتب‬ ‫زوج‬ ‫كل‬ ‫أن‬ ‫رأينا‬ ‫لقد‬
‫سمينا‬ ، ‫النقطة‬ ‫لنفس‬ ‫الصادي‬ ‫باالحداﻲﺛ‬ ‫نقطة‬ ‫لكل‬ ‫السيني‬ ‫االحداﻲﺛ‬ ‫تربﻂ‬ ‫معادلة‬ ‫وجدنا‬
‫نقاط‬ ‫تقع‬ ‫أن‬ ‫مثال‬ ‫اشرتﻃنا‬ ‫فلو‬ ( ‫تعينها‬ ‫املطلوب‬ ‫النقاط‬ ‫مجموعة‬ ‫معادلة‬ ) ‫املعادلة‬ ‫هذه‬
‫لنقطة‬ ‫السيني‬ ‫االحداﻲﺛ‬ ‫تربﻂ‬ ‫معادلة‬ ‫وأوجدنا‬ L ‫مستقيم‬ ‫عىل‬ ‫املستوي‬ ‫من‬ ‫جزئية‬ ‫مجموعة‬
‫املعادلة‬ ‫هذه‬ ‫نسمي‬ ‫فاننا‬ ‫الصادي‬ ‫باالحداﻲﺛ‬ ‫املجموعة‬ ‫هذه‬ ‫من‬ ‫اختيارية‬
. ( L ‫املستقيم‬ ‫معادلة‬ )
‫الصادات‬ ‫محور‬ ‫يوازي‬ L ‫كان‬ ‫اذا‬ (1
‫فان‬ a ‫بالبعد‬ ‫عنه‬ ‫ويبعد‬
x = a ‫معادلته‬
‫السينات‬ ‫محور‬ ‫يوازي‬ k ‫كان‬ ‫اذا‬ (2
‫فان‬ b ‫بالبعد‬ ‫عنه‬ ‫ويبعد‬
y = b ‫معادلته‬
‫توازي‬ ‫نوع‬ ‫معرفة‬ ‫ﻤﻳكن‬ ‫عامة‬ ‫وبصورة‬
: ‫السابقتﻦﻴ‬ ‫املعادلتﻦﻴ‬ ‫أحد‬ ‫معرفة‬ ‫خالل‬ ‫من‬ ‫املحورين‬ ‫أحد‬ ‫مع‬ ‫املستقيم‬
x = x1
‫هي‬ ( x1
, y1
) ‫بالنقطة‬ ‫وﻤﻳر‬ ‫الصادات‬ ‫ملحور‬ ‫املوازي‬ ‫املستقيم‬ ‫فمعادلة‬
. ‫الصادات‬ ‫محور‬ ‫عىل‬ ‫ينطبق‬ ‫سوف‬ ‫املستقيم‬ ‫فان‬ x1
= 0 ‫عندما‬
y = y1
‫هي‬ ( x1
, y1
) ‫بالنقطة‬ ‫وﻤﻳر‬ ‫السينات‬ ‫ملحور‬ ‫املوازي‬ ‫املستقيم‬ ‫معادلة‬ ‫و‬
Analytic GeometryAnalytic GeometryAnalytic GeometryAnalytic Geometry ‫االحداثية‬ ‫الهندسة‬ : ‫ابع‬‫ر‬‫ال‬ ‫الفصل‬
‫االحداﻲﺛ‬ ‫مستوي‬ ‫يف‬ ‫نقاط‬ ‫مجموعة‬ ‫معادلة‬ [4-1]
X
k
a
L
Y
b
{
{
Y
X

65. 65
. ‫السينات‬ ‫محور‬ ‫عىل‬ ‫ينطبق‬ ‫سوف‬ ‫املستقيم‬ ‫فان‬ y1
= 0 ‫عندما‬
x = 0 ‫هي‬ ‫الصادات‬ ‫محور‬ ‫ومعادلة‬ y = 0 ‫هي‬ ‫السينات‬ ‫محور‬ ‫معادلة‬ ‫فﺈن‬ : ‫سبق‬ ‫ومﺎﻤ‬
Equation of the line
: ‫بنقطتﻦﻴ‬ ‫مار‬ ‫ملستقيم‬ ‫الكارتزية‬ ‫املعادلة‬ (4 - 2 - 1)
‫بالنقطتﻦﻴ‬ ‫املار‬ ‫املستقيم‬ ‫معادلة‬ ‫فتكون‬ a ( x1
, y1
) ، b( x2
, y2
) ، c ( x , y ) ∈ ab ‫لنفرض‬
. a ، b
: ‫هي‬
. (3 , -1) ، (- 2 , 5 ) ‫بالنقطتﻦﻴ‬ ‫املار‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬
a (3 , -1) ، b (- 2 , 5 ) ، c ( x , y) ∈ ab / ‫الحـــل‬
∵ =
= ⇒ =
- 5y - 5 = 6 x - 18
. ‫املستقيم‬ ‫معادلة‬ 6x + 5 y - 13 = 0
y - y1
y2
-y1
x - x1
x2
- x1
y + 1 5+1
x - 3 -2- 3
‫املستقيم‬ ‫معادلة‬ [4-2]
y - y1
y2
-y1
x- x1
x2
- x1
=
1 ‫مثال‬
y + 1 6
x - 3 -5

66. 66
( 5, - 3 ) ‫والنقطة‬ ‫األصل‬ ‫بنقطة‬ ‫املار‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬
A ( - 3 , 5 ) ، O ( 0 , 0 ) ‫لتكن‬ / ‫الحــــل‬
= : ‫هي‬ OA‫املستقيم‬ ‫معادلة‬
= ⇒ =
5x = -3 y ⇒ 5x + 3y = 0
Slope of �e Line
‫فان‬ a ( x1
, y1
) ، b ( x2
, y2
) ‫كانﺖ‬ ‫اذا‬
x1
≠ x2
‫بﴩط‬ = ab ‫املستقيم‬ ‫ميل‬
( 1 , -1 ) , ( 3 ,-5) ‫بالنقطتﻦﻴ‬ ‫املار‬ ‫املستقيم‬ ‫ميل‬ ‫جد‬
m= ‫امليل‬ / ‫الحـــل‬
m = = = -2
y - y1
y2
-y1
x - x1
x2
- x1
2 ‫مثال‬
y - 0 5- 0
x - 0 -3- 0
y 5
x -3
: ‫املستقيم‬ ‫ميل‬ [4-3]
: ( 4 - 1 ) ‫تعريﻒ‬
y2
-y1
x2
- x1
3 ‫مثال‬
y2
-y1
x2
- x1
4
-2
-1 +5
1 -3

67. 67
‫اإلتجاه‬ ‫مع‬ L ‫املستقيم‬ ‫يصنعها‬ ‫التي‬ ‫املوجبة‬ ‫اوية‬‫ز‬‫ال‬ ‫قياس‬ ‫هي‬ ⊖ ‫كانﺖ‬ ‫إذا‬
: ‫فﺈن‬ ‫السينات‬ ‫ملحور‬ ‫املوجب‬
⊖ ∈ [0, 180ْ )/{ 90ْ } ‫حيث‬ tan ⊖ = L ‫املستقيم‬ ‫ميل‬
. ‫السينات‬ ‫ملحور‬ ‫املوجب‬ ‫االتجاه‬ ‫مع‬ 45ْ ‫يضع‬ ‫الذي‬ L1
‫املستقيم‬ ‫ميل‬ ‫(جد‬ ‫أ‬
. ‫السينات‬ ‫ملحور‬ ‫املوجب‬ ‫االتجاه‬ ‫مع‬ 150ْ ‫يضع‬ ‫الذي‬ L2
‫املستقيم‬ ‫ميل‬ ‫جد‬ (‫ب‬
tan ⊖ = ‫املستقيم‬ ‫ميل‬ / ‫لحــل‬‫ا‬
tan 45ْ = L1
‫ميل‬
1=
tan150ْ= L2
‫ميل‬ ‫كذلﻚ‬
tan ( 180ْ - 30 ) =
- tan 30 =
3
-1
: ( 4 - 2 ) ‫تعريﻒ‬
4 ‫مثال‬
Y
L2
L1
150ْ
45ْ X
°
°

68. 68
. 0 = ‫ميله‬ ‫السينات‬ ‫محور‬ ‫يوازي‬ ‫مستقيم‬ ‫أي‬ ‫أو‬ ‫السينات‬ ‫محور‬ (1)
. ‫معرف‬ ‫ﻏري‬ ‫ميله‬ ‫الصادات‬ ‫محور‬ ‫يوازي‬ ‫مستقيم‬ ‫أي‬ ‫أو‬ ‫الصادات‬ ‫محور‬ (2)
. m ‫وميله‬ a ( x1
, y1
) ‫بالنقطة‬ ‫املار‬ ‫املستقيم‬ ‫معادلة‬ (3)
= ‫هي‬ ‫نقطتﻦﻴ‬ ‫بداللة‬ ‫املستقيم‬ ‫معادلة‬
: ‫املعادلة‬ ‫فتصبﺢ‬ =m
(y - y1
) = m( x - x1
)
‫وميله‬ ( -3 , 4 ) ‫بالنقطة‬ ‫املار‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬
(y - y1
) = m( x - x1
) : ‫املعادلة‬
y - 4 = ( x+ 3 )
3y- 12 = 2x + 6
2x - 3y + 18 = 0
‫مع‬ 135ْ ‫يصنع‬ ‫والذي‬ ( -2 , 3 ) ‫بالنقطة‬ ‫ﻤﻳر‬ ‫الذي‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬
. ‫السينات‬ ‫ملحور‬ ‫املوجب‬ ‫االتجاه‬
( x1
, y1
) = ( -2 ,3 ) / ‫الحــل‬
m = tan 135 ْ
m = tan ( 180 ْ - 45ْ )
m = - tan 45ْ
y - y1
y2
-y1
x - x1
x2
- x1
y - y1
x - x1
: ‫نتيجة‬
5 ‫مثال‬2
3
2
3
6 ‫مثال‬

69. 69
m = - 1
(y - y1
) = m( x - x1
)
y - 3 = -1 ( x + 2 )
x + y - 1 = 0 ‫املستقيم‬ ‫معادلة‬
a ، b ، c ∈ R ‫حيث‬ a x + b y + c = 0 ‫هي‬ ‫مستقيم‬ ‫معادلة‬ ‫أن‬ ‫نفرض‬
. ‫ا‬‫ر‬‫صف‬ ‫معا‬ ‫اليساويا‬ a , b
( ‫السيني‬ ‫املقطع‬ ) x= ax + c = 0 y = 0 ‫بوضع‬ (1)
. ‫الصادي‬ ‫املحور‬ ‫يوازي‬ ‫مستقيم‬ ‫معادلة‬ ‫ومتثل‬
( ‫الصادي‬ ‫املقطع‬ ) y= by + c = 0 x = 0 ‫بوضع‬ (2)
. ‫السيني‬ ‫املحور‬ ‫يوازي‬ ‫مستقيم‬ ‫معادلة‬ ‫ومتثل‬
ax + b y + c = 0 ‫التقاﻃع‬ ‫بنقطتي‬ ‫املار‬ ‫املستقيم‬ ‫ميل‬ (3)
: ‫هﺎﻤ‬ ‫واللتان‬ ‫االحداثﻦﻴ‬ ‫املحورين‬ ‫مع‬
( , 0 ) , ( 0 , )
‫ميله‬ ‫يكون‬ a x + b y + c = 0 ‫معادلته‬ ‫الذي‬ ‫املستقيم‬ ‫أن‬ ‫القول‬ ‫خالصة‬
m= - = -
b ≠ 0 ‫وان‬ ‫املعادلة‬ ‫من‬ ‫واحد‬ ‫ﻃرف‬ ‫يف‬ x ، y ‫بﴩط‬
- c
a
: ‫معادلته‬ ‫من‬ ‫املستقيم‬ ‫ميل‬ ‫استنتاج‬ [4-4]
a
b
x ‫ﻣﻌﺎﻣﻞ‬
y ‫ﻣﻌﺎﻣﻞ‬
- c
b
- c
a
- c
b
⇒⇒
⇒ ⇒
y2
- y1
x2
- x1
m = =
- c
b
c
a
a
b
=

70. 70
. ‫والصادي‬ ‫السيني‬ ‫املقطعﻦﻴ‬ ‫جد‬ ‫ثم‬ 3x - 4y - 12 = 0 ‫املستقيم‬ ‫ميل‬ ‫جد‬
m= - = - = / ‫الحــل‬
. ‫السيني‬ ‫املقطع‬ y = 0 ⇒ 3x -12 = 0 ⇒ x= 4
. ‫الصادي‬ ‫املقطع‬ x = 0 ⇒ - 4y - 12 = 0 ⇒ y =- 3
‫متساويﻦﻴ‬ ‫ميالهﺎﻤ‬ ‫فان‬ ‫مستقيﺎﻤن‬ (Parallel) ‫توازى‬ ‫اذا‬ (1
m1
= m2
‫فان‬ L1
∥ L2
‫كان‬ ‫اذا‬ ‫اي‬
. ‫متوازيان‬ ‫فانهﺎﻤ‬ ‫مستقيمﻦﻴ‬ ‫ميال‬ ‫تساوى‬ ‫اذا‬ ‫وبالعكس‬ (2
a1
x+ b1
y+c1
=0 : ‫معادلته‬ L1
(3
a2
x+b2
y+c2
=0 : ‫معادلته‬ L2
m1
= m2
‫فان‬ L1
∥ L2
‫وعندما‬
= ‫أو‬ = ‫اي‬
-1 = ‫ميالهﺎﻤ‬ ‫ﴐب‬ ‫حاصل‬ ‫فان‬ ‫مستقيﺎﻤن‬ (Perpendicular) ‫تعامد‬ ‫إذا‬ (1
m1
× m2
‫فان‬ L1
⊥ L2
‫كان‬ ‫إذا‬ ‫أي‬
. ‫االشارة‬ ‫وبعكس‬ ‫اﻵخر‬ ‫مقلوب‬ = ‫أحدهﺎﻤ‬ ‫ميل‬ ‫ان‬ ‫أو‬
a
b
7 ‫مثال‬
3
- 4
3
4
: ‫متوازيﻦﻴ‬ ‫مستقيمﻦﻴ‬ ‫ميﲇ‬ ‫بﻦﻴ‬ ‫العالقة‬ [4-5]
- a1
b 1
-a 2
b 2
: ‫متعامدين‬ ‫مستقيمﻦﻴ‬ ‫ميﲇ‬ ‫بﻦﻴ‬ ‫العالقة‬ [4-6]
a1
b 1
a 2
b 2
=-1m1
= - ‫ﺍﻭ‬
1
m2

71. 71
3x -4y + 7 = 0 , 4x + 3y - 8 = 0 : ‫املستقيمﻦﻴ‬ ‫تعامد‬ ‫عىل‬ ‫برهن‬
m1
= ، m2
= /‫الحـــل‬
m1
× m 2
= × = - 1
∴ L1
⊥ L2
: ‫املستقيم‬ ‫ويوازي‬ ( - 2 , 1 ) ‫النقطة‬ ‫من‬ ‫ﻤﻳر‬ ‫الذي‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬
3y - 2x + 7 = 0
m= - = - = ‫املعلوم‬ ‫املستقيم‬ ‫ميل‬ /‫الحـــل‬
= ‫املطلوب‬ ‫املستقيم‬ ‫ميل‬ ⇐ ‫متوازيان‬ ‫املستقيﺎﻤن‬
‫هي‬ ‫وميل‬ ‫نقطة‬ ‫بداللة‬ ‫املستقيم‬ ‫معادلة‬ ∴
(y - y1
) = m( x - x1
)
y - 1 = (x + 2 )
3y - 3 = 2x+ 4 ⇒ ∴ 2x -3y + 7 = 0 ‫املستقيم‬ ‫معادلة‬
8 ‫مثال‬
3
4
- 4
3
3
4
- 4
3
9 ‫مثال‬
a
b
-(-2)
3
2
3
2
3
2
3

72. 72
: ‫املستقيم‬ ‫عىل‬ ‫وعمودي‬ (3 , -5) ‫بالنقطة‬ ‫ﻤﻳر‬ ‫الذي‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬
3x + y=1
-3 = ‫املعلوم‬ ‫املستقيم‬ ‫ميل‬ /‫الحـــل‬
= ‫املطلوب‬ ‫املستقيم‬ ‫ميل‬
‫متعامدين‬ ‫املستقيﺎﻤن‬ ‫ﻻﻥ‬
: ‫هي‬ ‫وميل‬ ‫نقطة‬ ‫بداللة‬ ‫املستقيم‬ ‫معادلة‬
(y - y1
) = m( x - x1
)
y+ 5 = (x - 3 )
3y +15 = x-3
. ‫املستقيم‬ ‫معادلة‬ ...... x - 3y - 18 = 0
10 ‫مثال‬
1
3
1
3

73. 73
: ‫أوال‬
. ( -2 , 0 ) ( 2 , 0 ) ‫بالنقطتﻦﻴ‬ ‫املار‬ ‫املستقيم‬ ‫ميل‬ ‫جد‬ (1)
‫ميل‬ ‫يكون‬ ‫بحيث‬ w‫قيمة‬ ‫فجد‬ ، a ( 2, 3) , b (w , -3 )‫كانﺖ‬ ‫اذا‬ (2)
. = ab
: ‫ثانيا‬
‫لكل‬ ‫الصحيحة‬ ‫االجابة‬ ‫حدد‬ . ‫صحيحة‬ ‫فقﻂ‬ ‫واحدة‬ ‫اجابات‬ ‫أربع‬ ‫يﺂﻲﺗ‬ ‫مﺎﻤ‬ ‫فقرة‬ ‫لكل‬
: ‫فقرة‬
= L ‫ميل‬ ‫فان‬ ( 3 , 2) ، (5,1) ‫بالنقطتﻦﻴ‬ ‫ﻤﻳر‬ M ، L ⊥M ‫كان‬ ‫اذا‬ (1)
. - (‫)د‬ ، (‫)جـ‬ ، 2 (‫)ب‬ ، (‫)أ‬
= L ‫ميل‬ ‫فان‬ (-2 , 3 ) , ( 2 ,- 3 ) ‫بالنقطتﻦﻴ‬ ‫ﻤﻳر‬ M , L ∥ M ‫كان‬ ‫اذا‬ (2)
. - (‫)د‬ , (‫)جـ‬ , (‫)ب‬ , (‫)أ‬
: ‫ثالثا‬
‫املار‬ M ‫املستقيم‬ ‫يوازي‬ ( - 1, 3 ) , (1 , 6) ‫بالنقطتﻦﻴ‬ ‫املار‬ L ‫املستقيم‬ ‫أن‬ ‫بﻦﻴ‬ (1)
. ( 0 , -1 ) (- 2 ,- 4 ) ‫بالنقطتﻦﻴ‬
‫عىل‬ ‫عمودي‬ ( 0 , 5 ), (2 , 0) ‫بالنقطتﻦﻴ‬ ‫املار‬ L ‫املستقيم‬ ‫أن‬ ‫بﻦﻴ‬ (2)
. ( 1 , - 1 ) ( 6 , 1 ) ‫بالنقطتﻦﻴ‬ ‫املار‬ M ‫املستقيم‬
(4-1) ‫متارين‬
1
2
1
2
2
3
2
3
3
2
- 3
2
2
3
2
3

74. 74
: ‫ابعا‬‫ر‬
. (0 , -4) ‫بالنقطة‬ ‫وﻤﻳر‬ = ‫ميله‬ ‫الذي‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬ (1)
. (2 , - 1) ‫بالنقطة‬ ‫وﻤﻳر‬ ‫السينات‬ ‫ملحور‬ ‫املوازي‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬ (2)
. (2 , - 1) ‫بالنقطة‬ ‫وﻤﻳر‬ ‫الصادات‬ ‫ملحور‬ ‫املوازي‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬ (3)
. (- 1 , 5 ) ، (- 1 , 3 ) ‫بالنقطتﻦﻴ‬ ‫املار‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬ (4)
‫الذي‬ ‫للمستقيم‬ ‫واملوازي‬ (2 ,-1 ) ‫بالنقطة‬ ‫املار‬ L ‫املستقيم‬ ‫معادلة‬ ‫جد‬ (5)
. = ‫ميله‬
‫الذي‬ ‫املستقيم‬ ‫عىل‬ ‫عموديا‬ ( 0 , - 2) ‫بالنقطة‬ ‫املار‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬ (6)
. = ‫ميله‬
‫مع‬150ْ ‫قياسها‬ ‫اوية‬‫ز‬ ‫يصنع‬ ‫والذي‬ (-1 ,- 5 ) ‫بالنقطة‬ ‫املار‬ ‫املستقيم‬ ‫معادلة‬ ‫)7(جد‬
. ‫السينات‬ ‫ملحور‬ ‫املوجب‬ ‫االتجاه‬
: ‫خامسا‬
: ‫يأﻲﺗ‬ ‫فيﺎﻤ‬ ‫مستقيم‬ ‫لكل‬ ‫والصادي‬ ‫السيني‬ ‫واملقطع‬ ‫امليل‬ ‫جد‬ (1)
L1
: 2x - 3y + 5 = 0 (‫أ‬
L2
: 8y = 4x + 16 (‫ب‬
L3
: 3y = -4 (‫جـ‬
1
2
2
3
- 3
5

75. 75
: ‫معادلته‬ ‫الذي‬ ‫املستقيم‬ ‫ويوازي‬ (2 , - 5) ‫بالنقطة‬ ‫املار‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬ (2)
2x - y +3 = 0
‫الذي‬ ‫املستقيم‬ ‫عىل‬ ‫عموديا‬ (2 , - 2) ‫بالنقطة‬ ‫املار‬ ‫املستقيم‬ ‫معادلة‬ ‫جد‬ (3)
x + y = 0 ‫معادلته‬
: ً‫ا‬‫سادس‬
‫فجد‬ 5x + 2y = 11 : ‫هي‬ M ‫ومعادلة‬ wx - 8y = 7 : ‫هي‬ L ‫معادلة‬ ‫كان‬ ‫إذا‬
: ‫كان‬ ‫إذا‬ w ‫قيمة‬
. L ∥ M (1)
. L ⊥ M (2)

76. 76

77. 77
‫يتم‬ ،‫دقتها‬ ‫من‬ ‫والتاكد‬ ‫اجعتها‬‫ر‬‫وم‬ ‫امليدان‬ ‫من‬ ‫االحصائية‬ ‫البيانات‬ ‫عىل‬ ‫الحصول‬ ‫بعد‬
‫املتوسطة‬ ‫املرحلة‬ ‫ﻃالب‬ ‫م‬ّ‫ل‬‫تع‬ ‫كﺎﻤ‬ ، ‫فهمها‬ ‫يسهل‬ ‫لﻲﻜ‬ ‫مبسطة‬ ‫بطريقة‬ ‫البيانات‬ ‫هذه‬ ‫عرض‬
. ‫مناسبة‬ ‫اخرى‬ ‫رسوم‬ ‫اي‬ ‫أو‬ ‫بيانية‬ ‫رسوم‬ ‫أو‬ ‫جداول‬ ‫بواسطة‬ ‫يتم‬ ‫العرض‬ ‫هذا‬ ‫ان‬
‫البيانات‬ ‫من‬ ‫النوعﻦﻴ‬ ‫لكال‬ ‫الجدولية‬ ‫العروض‬ ‫عىل‬ ‫السابقة‬ ‫استه‬‫ر‬‫د‬ ‫يف‬ ‫الطالب‬ ‫رف‬ّ‫ع‬‫ت‬ ‫وقد‬
‫ن‬ّ‫و‬‫ك‬ ‫كﺎﻤ‬ ‫كمية‬ ‫او‬ ‫كيفية‬ ‫لبيانات‬ ‫ارية‬‫ر‬‫تك‬ ‫جداول‬ ‫وكون‬ ‫كمية‬ ‫او‬ ‫كيفية‬ ‫بيانات‬ ‫كانﺖ‬ ‫سواء‬
‫او‬ ‫الدوائر‬ ‫او‬ ‫املنحنيات‬ ‫بواسطة‬ ‫البيانات‬ ‫هذه‬ ‫بعرض‬ ‫وقام‬ ، ‫الفﺌات‬ ‫ذات‬ ‫ارية‬‫ر‬‫تك‬ ‫جداول‬
‫سنتعرف‬ ‫البند‬ ‫هذا‬ ‫ويف‬ ‫املتجمعة‬ ‫املنحنيات‬ ‫او‬ ‫ارية‬‫ر‬‫التك‬ ‫املضلعات‬ ‫او‬ ‫ارية‬‫ر‬‫التك‬ ‫املدرجات‬
‫الالحقة‬ ‫الطالب‬ ‫اسة‬‫ر‬‫د‬ ‫يف‬ ‫اما‬ ، ‫القادمة‬ ‫البنود‬ ‫يف‬ ‫اليها‬ ‫لحاجتنا‬ ‫املتجمعة‬ ‫املنحنيات‬ ‫عىل‬
: ‫أهمها‬ ‫ومن‬ ‫هامة‬ ‫أخرى‬ ‫منحنيات‬ ‫عىل‬ ‫سيتعرف‬
‫تطبيقات‬ ‫ستجد‬ ‫كﺎﻤ‬ ‫امللتوية‬ ‫املنحنيات‬ ، ‫اﻵﳼ‬ ‫املنحني‬ ، ‫النوين‬ ‫املنحني‬ ، ‫الطبيعي‬ ‫املنحني‬ )
. ( ‫وعلمية‬ ‫حياتية‬
‫تفصيلية‬ ‫فكرة‬ ‫يعطينا‬ ‫التاﱄ‬ ‫والجدول‬ ‫الفﺌات‬ ‫ذات‬ ‫ارية‬‫ر‬‫التك‬ ‫الجداول‬ ‫سبق‬ ‫فيﺎﻤ‬ ‫تناولنا‬
‫بالكيلو‬ ‫الوزن‬ ‫فﺌات‬ ‫حسب‬ ‫املخازن‬ ‫احدى‬ ‫يف‬ ‫السلع‬ ‫توزيع‬ : ‫الفﺌات‬ ‫حسب‬ ‫التوزيع‬ ‫عن‬
‫ام‬‫ر‬‫ﻏ‬
(١) ‫رقم‬ ‫الجدول‬
Statistics ‫اإلحصاء‬ : ‫الخامس‬ ‫الفصل‬
‫مقدمة‬ [5-1]
: ‫اﳌﺘﺠﻤﻌﺔ‬ ‫اﳌﻨﺤﻨﻴﺎت‬ [5-2]
(١) ‫رقم‬ ‫الجدول‬
(‫السلع‬ ‫)عدد‬ ‫ار‬‫ر‬‫التك‬ (‫)كﻐم‬ ‫الوزن‬ ‫فﺌات‬
2 20-
4 25-
5 30-
7 35-
12 40-
8 45-
7 50-
5 55-60

78. 78
30 ‫من‬ ‫اقل‬ ‫اﱃ‬ ‫كﻐم‬ 25 ‫بﻦﻴ‬ ‫وزنها‬ ‫اوح‬‫رت‬‫ي‬ ‫التي‬ ‫السلع‬ ‫عدد‬ ‫أن‬ ‫نجد‬ (1) ‫رقم‬ ‫الجدول‬ ‫من‬
‫سلع‬ (7) ‫هي‬ ‫كﻐم‬ 55 ‫إﱃ‬ 50 ‫بﻦﻴ‬ ‫وزنها‬ ‫اوح‬‫رت‬‫ي‬ ‫التي‬ ‫السلع‬ ‫عدد‬ ‫وكذلﻚ‬ ‫سلع‬ (4) ‫هي‬ ‫كﻐم‬
ً‫ال‬‫فمث‬ ‫التفصيلية‬ ‫البيانات‬ ‫من‬ ‫بدال‬ ‫اجﺎﻤلية‬ ‫اخرى‬ ‫بيانات‬ ‫عىل‬ ‫التعرف‬ ‫يهمنا‬ ‫احيانا‬ ‫ولكن‬
‫سلع‬ 6 ‫الحالة‬ ‫هذه‬ ‫يف‬ ‫وهي‬ ‫كﻐم‬ 30 ‫عن‬ ‫انها‬‫ز‬‫او‬ ‫تقل‬ ‫التي‬ ‫السلع‬ ‫عدد‬ ‫معرفة‬ ‫إﱃ‬ ‫نحتاج‬
‫السلع‬ ‫عدد‬ ‫معرفة‬ ‫إﱃ‬ ‫نحتاج‬ ‫وكذلﻚ‬ ‫والثانية‬ ‫األوﱃ‬ ‫الفﺌتﻦﻴ‬ ‫يف‬ ‫ات‬‫ر‬‫ا‬‫ر‬‫التك‬ ‫بجمع‬ ‫عليها‬ ‫وتحصل‬
‫الفﺌات‬ ‫يف‬ ‫ات‬‫ر‬‫ا‬‫ر‬‫التك‬ ‫بجمع‬ ‫عليها‬ ‫ونحصل‬ ‫سلعة‬ (20) ‫هي‬ ‫فاكرث‬ ‫كﻐم‬ 45 ‫انها‬‫ز‬‫او‬ ‫تبلﻎ‬ ‫التي‬
‫تجميع‬ ‫يتم‬ ‫الجدول‬ ‫هذا‬ ‫ويف‬ ‫متجمعة‬ ‫ارية‬‫ر‬‫تك‬ ‫جداول‬ ‫تكوين‬ ‫إﱃ‬ ‫نحتاج‬ ‫لذلﻚ‬ ‫األخرية‬ ‫الثالثة‬
: ‫نوعان‬ ‫ارية‬‫ر‬‫التك‬ ‫والجداول‬ ‫اﻵخر‬ ‫الطرف‬ ‫إﱃ‬ ‫الجدول‬ ‫ﻃريف‬ ‫أحد‬ ‫من‬ ‫ات‬‫ر‬‫ا‬‫ر‬‫التك‬
: ‫الصاعد‬ ‫املتجمع‬ ‫الجدول‬ : ‫أوال‬
‫الفﺌات‬ ‫جهة‬ ‫إﱃ‬ ‫الصﻐرية‬ ‫الفﺌات‬ ‫جهة‬ ‫من‬ ‫ات‬‫ر‬‫ا‬‫ر‬‫التك‬ ‫تجميع‬ ‫يتم‬ ‫الجداول‬ ‫من‬ ‫النوع‬ ‫هذا‬ ‫يف‬
‫األول‬ : ‫عمودين‬ ‫من‬ ‫الجدول‬ ‫هذا‬ ‫ويتكون‬ ( ‫أسفله‬ ‫إﱃ‬ ‫اري‬‫ر‬‫التك‬ ‫الجدول‬ ‫أعىل‬ ‫من‬ ‫)اي‬ ‫الكبرية‬
: ‫اﻵﻲﺗ‬ ‫املثال‬ ‫يف‬ ‫كﺎﻤ‬ ‫الصاعد‬ ‫املتجمع‬ ‫ار‬‫ر‬‫للتك‬ ‫والثاين‬ ‫للفﺌات‬ ‫العليا‬ ‫للحدود‬
(1) ‫رقم‬ ‫الجدول‬ ‫يف‬ ‫املوجودة‬ ‫للبيانات‬ ‫الصاعد‬ ‫املتجمع‬ ‫الجدول‬ ‫كون‬
/ ‫الحـــل‬
. ‫عمودين‬ ‫من‬ ً‫ال‬‫جدو‬ ‫نكون‬ (1)
‫كﻐم‬ 30 ‫من‬ ‫اقل‬ ، ‫كﻐم‬ 25 ‫من‬ ‫أقل‬ ‫وهي‬ ‫للفﺌات‬ ‫العليا‬ ‫للحدود‬ ‫األول‬ ‫العمود‬ ‫يخصﺺ‬ (2)
. ‫وهكذا‬ ... ،
‫رقم‬ ‫الجدول‬ ‫من‬ ‫عليه‬ ‫نحصل‬ ‫التي‬ ‫الصاعدة‬ ‫املتجمعة‬ ‫ارات‬‫ر‬‫للتك‬ ‫الثاين‬ ‫العمود‬ ‫يخصﺺ‬ (3)
‫أقل‬ ‫التي‬ ‫القيم‬ ‫ات‬‫ر‬‫ا‬‫ر‬‫وتك‬ . 2 ‫هي‬ 25 ‫من‬ ‫اقل‬ ‫التي‬ ‫القيم‬ ‫ات‬‫ر‬‫ا‬‫ر‬‫تك‬ ‫عدد‬ ‫أن‬ ‫نجد‬ ‫حيث‬ (1)
‫التاﱄ‬ ‫ار‬‫ر‬‫التك‬ ‫نضيﻒ‬ ‫وهكذا‬ ، 2+4+5 =11‫هي‬ 35 ‫من‬ ‫أقل‬ ‫والتي‬ 2 + 4 = 6 ‫هي‬ 30 ‫من‬
‫متجمع‬ ‫ار‬‫ر‬‫تك‬ ‫كﺂخر‬ ‫ات‬‫ر‬‫ا‬‫ر‬‫التك‬ ‫مجموع‬ ‫إﱃ‬ ‫نصل‬ ‫حتﻰ‬ ‫خطوة‬ ‫كل‬ ‫يف‬ ‫السابق‬ ‫املجموع‬ ‫إﱃ‬
. (2) ‫رقم‬ ‫الجدول‬ ‫يف‬ ‫كﺎﻤ‬
1 ‫مثال‬

79. 79
‫ام‬‫ر‬‫ﻏ‬ ‫بالكيلو‬ ‫الوزن‬ ‫حسب‬ ‫السلع‬ ‫لتوزيع‬ ‫الصاعد‬ ‫املتجمع‬ ‫الجدول‬
(2) ‫رقم‬ ‫الجدول‬
: ‫النازل‬ ‫املتجمع‬ ‫الجدول‬ : ً‫ا‬‫ثاني‬
‫من‬ ‫)اي‬ ‫الصﻐرية‬ ‫الفﺌات‬ ‫جهة‬ ‫إﱃ‬ ‫الكبرية‬ ‫الفﺌات‬ ‫جهة‬ ‫من‬ ‫ات‬‫ر‬‫ا‬‫ر‬‫التك‬ ‫تجمع‬ ‫الجدول‬ ‫هذا‬ ‫يف‬
‫الدنيا‬ ‫للحدود‬ ‫األول‬ ‫عمودين‬ ‫من‬ ً‫ا‬‫أيض‬ ‫الجدول‬ ‫هذا‬ ‫ويتكون‬ ( ‫اعاله‬ ‫إﱃ‬ ‫اري‬‫ر‬‫التك‬ ‫الجدول‬ ‫أسفل‬
: ‫اﻵﻲﺗ‬ ‫املثال‬ ‫يف‬ ‫كﺎﻤ‬ . ‫النازل‬ ‫املتجمع‬ ‫ار‬‫ر‬‫للتك‬ ‫والثاين‬ ‫للفﺌات‬
. (1) ‫رقم‬ ‫الجدول‬ ‫يف‬ ‫املوجودة‬ ‫للبيانات‬ ‫النازل‬ ‫املتجمع‬ ‫الجدول‬ ‫كون‬
/ ‫الحــل‬
. ‫عمودين‬ ‫من‬ ً‫ال‬‫جدو‬ ‫نكون‬ (1)
....‫وهكذا‬ ، ‫فاكرث‬ 25، ‫فاكرث‬ ‫كﻐم‬ 20 ‫وهي‬ ‫للفﺌات‬ ‫الدنيا‬ ‫للحدود‬ ‫األول‬ ‫العمود‬ ‫نخصﺺ‬ (2)
(1) ‫رقم‬ ‫الجدول‬ ‫من‬ ‫عليها‬ ‫نحصل‬ ‫التي‬ ‫النازلة‬ ‫املتجمعة‬ ‫ات‬‫ر‬‫ا‬‫ر‬‫للتك‬ ‫الثاين‬ ‫العمود‬ ‫نخصﺺ‬ (3)
: ‫املثال‬ ‫سبيل‬ ‫عىل‬ ‫نجد‬ ‫حيث‬
‫الصاعد‬ ‫املتجمع‬ ‫ار‬‫ر‬‫التك‬ ‫للفﺌات‬ ‫العليا‬ ‫الحدود‬
2 ‫كﻐم‬ 25 ‫من‬ ‫اقل‬
6 ‫كﻐم‬ 30 ‫من‬ ‫اقل‬
11 ‫كﻐم‬ 35 ‫من‬ ‫اقل‬
18 ‫كﻐم‬ 40 ‫من‬ ‫اقل‬
30 ‫كﻐم‬ 45 ‫من‬ ‫اقل‬
38 ‫كﻐم‬ 50 ‫من‬ ‫اقل‬
45 ‫كﻐم‬ 55 ‫من‬ ‫اقل‬
50 ‫كﻐم‬ 60 ‫من‬ ‫اقل‬
2 ‫مثال‬

80. 80
‫هو‬ ‫فأكرث‬ 25 ‫تساوي‬ ‫التي‬ ‫القيم‬ ‫ار‬‫ر‬‫تك‬ ‫وان‬ 50 ‫هي‬ ‫فأكرث‬ 20 ‫تساوي‬ ‫التي‬ ‫القيم‬ ‫ارت‬‫ر‬‫تك‬ ‫ان‬
‫يف‬ ‫السابق‬ ‫ار‬‫ر‬‫التك‬ ‫نطرح‬ ‫وهكذا‬ 50 - 4 - 2 =44 ‫هو‬ ‫فأكرث‬ 30 ‫تساوي‬ ‫والتي‬ 50 - 2 = 48
‫يف‬ ‫وذلﻚ‬ ‫نازل‬ ‫متجمع‬ ‫ار‬‫ر‬‫تك‬ ‫كﺂخر‬ (1) ‫رقم‬ ‫الجدول‬ ‫يف‬ ‫ار‬‫ر‬‫تك‬ ‫آخر‬ ‫اﱃ‬ ‫نصل‬ ‫حتﻰ‬ ‫خطوة‬ ‫كل‬
. (3) ‫رقم‬ ‫الجدول‬
(3) ‫رقم‬ ‫الجدول‬
: ‫الصاعد‬ ‫املتجمع‬ ‫املنحني‬ (‫)أ‬
‫األفقي‬ ‫املحور‬ ‫ونخصﺺ‬ ، ‫متعامدين‬ ‫محورين‬ ‫نرسم‬ ، ‫الصاعد‬ ‫املتجمع‬ ‫املنحني‬ ‫لتمثيل‬
‫بحيث‬ ‫الﺸكل‬ ‫عىل‬ ‫النقﻂ‬ ‫نؤﴍ‬ ‫ثم‬ ، ‫املتجمعة‬ ‫ات‬‫ر‬‫ا‬‫ر‬‫للتك‬ ‫والرأﳼ‬ ، ‫للفﺌات‬ ‫العليا‬ ‫للحدود‬
‫بخﻂ‬ ‫النقﻂ‬ ‫هذه‬ ‫نصل‬ ‫ثم‬ ‫للفﺌات‬ ‫العليا‬ ‫الحدود‬ ‫هي‬ ‫للنقاط‬ ‫السينية‬ ‫االحداثيات‬ ‫تكون‬
. ‫الكﲇ‬ ‫ار‬‫ر‬‫بالتك‬ ‫وينتهي‬ ‫متجمع‬ ‫ار‬‫ر‬‫تك‬ ‫أصﻐر‬ ‫من‬ ‫يبدأ‬ ‫صاعد‬ ‫منحنﻰ‬ ‫لدينا‬ ‫ليتكون‬ ‫ممهد‬
‫النازل‬ ‫املتجمع‬ ‫ار‬‫ر‬‫التك‬ ‫للفﺌات‬ ‫العليا‬ ‫الحدود‬
50 ‫فاكرث‬ 20
48 ‫52فاكرث‬
44 ‫فاكرث‬ 30
39 ‫فاكرث‬ 35
32 ‫فاكرث‬ 40
20 ‫فاكرث‬ 45
12 ‫فاكرث‬ 50
5 ‫فاكرث‬ 55
‫اﻟﺒﻴﺎﻧﺎت‬ ‫ﲤﺜﻴﻞ‬

81. 81
. (2) ‫رقم‬ ‫الجدول‬ ‫بيانات‬ ‫من‬ ‫الصاعد‬ ‫املتجمع‬ ‫املنحنﻰ‬ ‫ارسم‬
‫حسب‬ ‫األفقي‬ ‫املحور‬ ‫ونقسم‬ ، ‫متعامدين‬ ‫محورين‬ ‫نرسم‬ / ‫الحـــل‬
‫إﱃ‬ ‫الرأﳼ‬ ‫املحور‬ ‫ونقسم‬ 25 , 30 ..... ‫وهي‬ ‫الجدول‬ ‫يف‬ ‫املوجودة‬ ‫للفﺌات‬ ‫العليا‬ ‫الحدود‬
‫األعىل‬ ‫الحد‬ ‫بأخذ‬ ‫وذلﻚ‬ ‫النقﻂ‬ ‫نؤﴍ‬ ‫ثم‬ . ‫ات‬‫ر‬‫ا‬‫ر‬‫التك‬ ‫مجموع‬ ‫تﺸمل‬ ‫بحيث‬ ، ‫متساوية‬ ‫اقسام‬
‫نصل‬ ‫ثم‬ , ( 60,50 ) .... ، ( 30 , 6), ( 25 ، 2) ‫اي‬ ، ‫الصاعد‬ ‫املتجمع‬ ‫ار‬‫ر‬‫التك‬ ‫مع‬ ‫للفﺌة‬
.(5-1) ‫الﺸكل‬ ‫يف‬ ‫كﺎﻤ‬ ‫الصاعد‬ ‫املتجمع‬ ‫املنحني‬ ‫عىل‬ ‫بذلﻚ‬ ‫فنحصل‬ ، ‫ممهد‬ ‫بخﻂ‬ ‫النقﻂ‬ ‫هذه‬
25 30 35 40 45 50 55
50
45
40
35
30
25
20
15
10
5 ‫للفﺌات‬ ‫العليا‬ ‫الحدود‬
‫الصاعد‬‫املتجمع‬‫ار‬‫ر‬‫التك‬
60
: ‫النازل‬ ‫املتجمع‬ ‫املنحنﻰ‬ (‫)ب‬
‫للحدود‬ ‫ااالفقي‬ ‫املحور‬ ‫ونخصﺺ‬ ، ‫متعامدين‬ ‫محورين‬ ‫نرسم‬ ، ‫الصاعد‬ ‫املتجمع‬ ‫املنحﻰ‬ ‫يف‬ ‫كﺎﻤ‬
‫نؤﴍ‬ ‫ثم‬ (‫نازل‬ ‫متجمع‬ ‫ار‬‫ر‬‫تك‬ ‫أعىل‬ ‫)أو‬ ‫النازلة‬ ‫املتجمعة‬ ‫ات‬‫ر‬‫ا‬‫ر‬‫للتك‬ ‫والرأﳼ‬ ، ‫للفﺌات‬ ‫الدنيا‬
‫ات‬‫ر‬‫ا‬‫ر‬‫والتك‬ ‫للفﺌات‬ ‫الدنيا‬ ‫الحدود‬ ‫هي‬ ‫النقﻂ‬ ‫احداثيات‬ ‫تكون‬ ‫بحيث‬ ‫املحورين‬ ‫عىل‬ ‫النقﻂ‬
‫الذي‬ ‫النازل‬ ‫املتحمع‬ ‫املنحنﻰ‬ ‫عىل‬ ‫فنحصل‬ ‫ممهد‬ ‫بخﻂ‬ ‫النقﻂ‬ ‫هذه‬ ‫نصل‬ ‫ثم‬ ، ‫النازلة‬ ‫املتجمعة‬
. ‫متجمع‬ ‫ار‬‫ر‬‫تك‬ ‫بﺂخر‬ ‫وينتهي‬ ‫ارت‬‫ر‬‫للتك‬ ‫الكﲇ‬ ‫املجوع‬ ‫من‬ ‫يبدأ‬
‫الصاعد‬ ‫املتجمع‬ ‫ار‬‫ر‬‫التك‬ ( 5 - 1 ) ‫الﺸكل‬
3 ‫مثال‬

82. 82
20 25 30 35 40 45 50
50
45
40
35
30
25
20
15
10
5
‫للفﺌات‬ ‫العليا‬ ‫الحدود‬
‫النازل‬‫املتجمع‬‫ار‬‫ر‬‫التك‬
55
‫النازل‬ ‫املتجمع‬ ‫ار‬‫ر‬‫التك‬ ( 5 - 2 ) ‫الﺸكل‬

83. 83
Measures of Central Tendency
: ‫مقدمة‬ ( 5 - 3 - 1)
‫نريد‬ ‫واﻵن‬ ً‫ا‬‫وبياني‬ ً‫ا‬‫جدولي‬ ‫وعرضها‬ ‫البيانات‬ ‫جمع‬ ‫ائق‬‫ر‬‫ﻃ‬ ‫السابقة‬ ‫اسية‬‫ر‬‫الد‬ ‫احل‬‫ر‬‫امل‬ ‫يف‬ ‫اخذنا‬
. ‫لها‬ ً‫ال‬‫وممث‬ ‫اسة‬‫ر‬‫الد‬ ‫موضوع‬ ‫الظاهرة‬ ‫عن‬ ً‫ا‬‫ﱪ‬‫مع‬ ‫يكون‬ ‫مقياس‬ ‫عن‬ ‫نبحث‬ ‫أن‬
‫ما‬ ‫بلد‬ ‫يف‬ ً‫ال‬‫مث‬ ‫الدخل‬ ‫فمتوسﻂ‬ . ‫القيم‬ ‫جميع‬ ‫عن‬ ‫تعﱪ‬ ‫واحدة‬ ‫قيمة‬ ‫عىل‬ ‫الحصول‬ ‫نريد‬ ‫أي‬
. ‫للدخل‬ ‫العام‬ ‫املستوي‬ ‫عن‬ ‫يعﱪ‬ ‫أي‬ ‫البلد‬ ‫هذا‬ ‫يف‬ ‫الدخول‬ ‫جميع‬ ‫عن‬ ‫يعﱪ‬
‫معينة‬ ‫قيمة‬ ‫حول‬ ‫ترتكز‬ ‫ألن‬ ً‫ال‬‫مي‬ ‫أو‬ ‫نزعة‬ ‫لها‬ ‫ان‬ - ( ‫بيانات‬ ‫)اي‬ - ‫البيانات‬ ‫خصائﺺ‬ ‫ومن‬
‫النزعة‬ ‫مقاييس‬ ‫أو‬ ‫باملتوسطات‬ ‫تسمﻰ‬ ‫البيانات‬ ‫حولها‬ ‫ترتكز‬ ‫التي‬ ‫القيم‬ ‫وهذه‬ ‫متوسطة‬
‫درستها‬ ‫أن‬ ‫بعد‬ ‫التوسع‬ ‫من‬ ‫بﴚء‬ ‫املركزية‬ ‫النزعة‬ ‫مقاييس‬ ‫أهم‬ ‫نتناول‬ ‫وسوف‬ . ‫املركزية‬
: ‫وهي‬ ‫بسيﻂ‬ ‫بﺸكل‬ ‫املتوسطة‬ ‫املرحلة‬ ‫يف‬
. ‫الحسايب‬ ‫الوسﻂ‬ *
. ‫الوسيﻂ‬ *
. ‫املنوال‬ *
‫اياه‬‫ز‬‫م‬ ‫منها‬ ‫لكل‬ ‫كﺎﻤ‬ ‫الحساب‬ ‫وﻃريقة‬ ‫الفكرة‬ ‫حيث‬ ‫من‬ ‫الثالثة‬ ‫املقاييس‬ ‫هذه‬ ‫وتختلﻒ‬
. ‫اﻵخر‬ ‫دون‬ ‫املقاييس‬ ‫أحد‬ ‫فيها‬ ‫يستخدم‬ ‫التي‬ ‫الحاالت‬ ‫بعض‬ ‫هناك‬ ‫أن‬ ‫كﺎﻤ‬ . ‫وعيوبه‬
Arithmatic Mean
‫محل‬ ‫حلﺖ‬ ‫لو‬ ‫التي‬ ‫القيمة‬ ‫أنه‬ : ‫القيم‬ ‫من‬ ‫ملجموعة‬ ‫الحسايب‬ ‫الوسﻂ‬ ‫يعرف‬
ً‫ا‬‫مساوي‬ ‫الجديدة‬ ‫القيم‬ ‫هذه‬ ‫مجموع‬ ‫لكان‬ ‫املجموعة‬ ‫يف‬ ‫مفردة‬ ‫كل‬ ‫قيمة‬
‫القيم‬ ‫مجموع‬ ‫يساوي‬ ‫الحسايب‬ ‫الوسﻂ‬ ‫فﺈن‬ ‫وبالتاﱄ‬ ‫األصلية‬ ‫القيم‬ ‫ملجموع‬
.X ‫له‬ ‫ويرمز‬ ‫عددها‬ ‫عىل‬
:‫املركزية‬ ‫النزعة‬ ‫مقاييس‬ [5-3]
: ‫الحسايب‬ ‫الوسﻂ‬ [ 5 - 4 ]
: ( 5 - 1 ) ‫تعريﻒ‬

84. 84
: ‫الحسايب‬ ‫الوسﻂ‬ ‫حساب‬ ‫ﻃريقة‬
: ‫املبوبة‬ ‫ﻏري‬ ‫البيانات‬ / ً‫ال‬‫أو‬
= ‫الحسايب‬ ‫الوسﻂ‬
x= ‫وبالرموز‬
: ‫هي‬ ‫اشخاص‬ ‫خمسة‬ ‫اعﺎﻤر‬ ‫كانﺖ‬ ‫اذا‬
‫الحسايب‬ ‫الوسﻂ‬ ‫احسب‬ ، ‫سنة‬ 12 ، ‫سنة‬ 11 ، ‫سنوات‬ 9 ، ‫سنوات‬ 8 ، ‫سنوات‬ 5
. ‫األشخاص‬ ‫هؤالء‬ ‫العﺎﻤر‬
= ‫الحسايب‬ ‫الوسﻂ‬ / ‫الحـــل‬
x=
x = = 9
: ‫املبوبة‬ ‫البيانات‬ ‫يف‬ / ً‫ا‬‫ثاني‬
‫استخدام‬ ‫فيمكن‬ ‫بسيﻂ‬ ‫اري‬‫ر‬‫تك‬ ‫توزيع‬ ‫يف‬ ‫متجمعة‬ ‫االحصائية‬ ‫القيم‬ ‫كانﺖ‬ ‫اذا‬
: ‫اﻵﻲﺗ‬ ‫القانون‬
= ‫الحسايب‬ ‫الوسﻂ‬
x =
‫القيم‬ ‫مجموع‬
‫عددها‬
5+ 8 +9+11+ 12
5
‫القيم‬ ‫مجموع‬
‫عددها‬
45
5
‫ات‬‫ر‬‫ا‬‫ر‬‫التك‬ ‫مجموع‬
‫ارها‬‫ر‬‫تك‬ ‫يف‬ ‫فﺌة‬ ‫مركز‬ ‫كل‬ ‫ﴐب‬ ‫حاصل‬ ‫مجموع‬
x1
f1
+ x2
f2
+ .......+ xn
fn
f1
+ f2
+ .......... +fn
x1
+ x2
+ ....... +xn
n
5 ‫مثال‬
: ‫البسيﻂ‬ ‫اري‬‫ر‬‫التك‬ ‫للتوزيع‬ ‫الحسايب‬ ‫الوسﻂ‬ [5 - 4 - 1 ]

85. 85
i= 1، 2 ، 3 .......n x=
‫املجموع‬ ‫رمز‬ ‫هو‬ ‫مالحظة‬
‫كل‬ ‫عمر‬ ‫اشخاص‬ (5)‫و‬ ، ‫سنوات‬ 8 ‫منهم‬ ‫كل‬ ‫عمر‬ ‫اشخاص‬ (3) ‫هناك‬ ‫أن‬ ْ‫ب‬َ‫ه‬
‫كل‬ ‫عمر‬ ‫اثنﻦﻴ‬ ‫وشخصﻦﻴ‬ ‫سنة‬ 11 ‫منهم‬ ‫عمر‬ ‫اشخاص‬ 4‫و‬ ‫سنوات‬ 9 ‫منهم‬
: ‫التاﱄ‬ ‫الجدول‬ ‫يف‬ ‫كﺎﻤ‬ ‫سنة‬ 12 ‫منهم‬
‫الوسﻂ‬ ‫احسب‬ . ‫الفﺌة‬ ‫مركز‬ ‫ﻤﻳثل‬ ‫الذي‬ ‫هو‬ ‫االعﺎﻤر‬ ‫عدد‬ ‫فيكون‬ (‫فﺌات‬ ‫دون‬ ‫من‬ ‫الجدول‬ ‫)هذا‬
.‫للعمر‬ ‫الحسايب‬
‫فﺈن‬ f ‫بالرمز‬ ‫ار‬‫ر‬‫التك‬ ‫او‬ ‫االشخاص‬ ‫ولعدد‬ x ‫بالرمز‬ ‫للعمر‬ ‫رمزنا‬ ‫اذا‬ / ‫الحـــل‬
: ‫التاﱄ‬ ‫الجدول‬ ‫يف‬ ‫كﺎﻤ‬ ‫تبسيطها‬ ‫ﻤﻳكن‬ ‫الحل‬ ‫خطوات‬
x =
x = =9.786
xi
fi
fi
6 ‫مثال‬
‫الوسﻂ‬ ‫احسب‬ . ‫الفﺌة‬ ‫مركز‬ ‫ﻤﻳثل‬ ‫الذي‬ ‫هو‬ ‫االعﺎﻤر‬ ‫عدد‬ ‫فيكون‬ (‫فﺌات‬ ‫دون‬ ‫من‬ ‫الجدول‬ ‫)هذا‬
‫االشخاص‬ ‫عدد‬‫العمر‬
38
59
411
212
(x.f)‫ار‬‫ر‬‫العمر×التك‬(f) ‫ار‬‫ر‬‫)التك‬(x) ‫العمر‬
8×3 = 2438
9×5 = 4559
11×4 = 44411
12×2 = 24212
13714
137
14
∑
∑
∑
x i
f i
fi
∑
∑
∑(xf)=∑f=

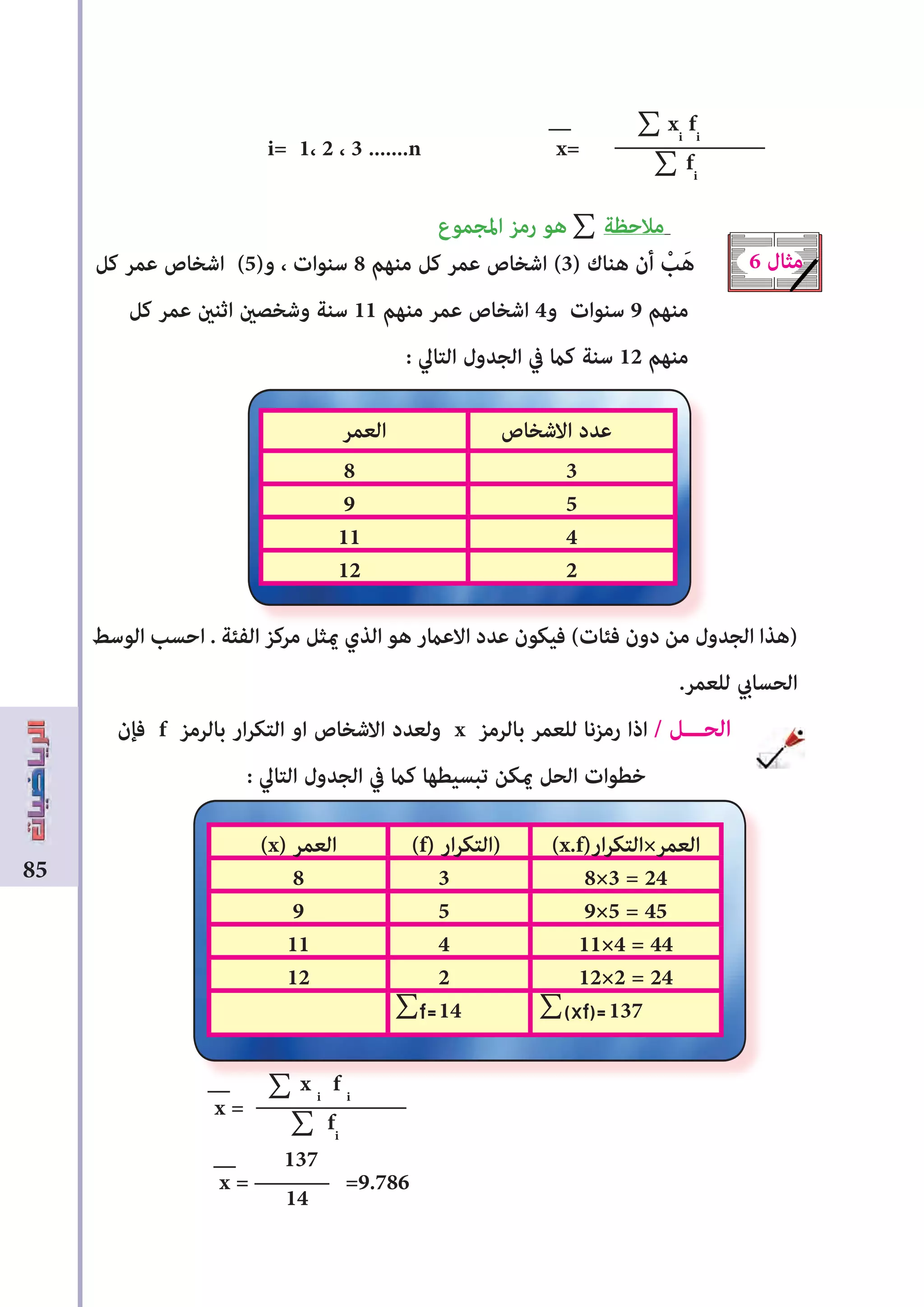
86. 86
. ‫الفﺌات‬ ‫ذات‬ ‫ارية‬‫ر‬‫التك‬ ‫الجداول‬ ‫حالة‬ ‫ونأخذ‬ ‫أخرى‬ ‫خطوة‬ ‫ولنتقدم‬
‫حسب‬ ‫شخﺺ‬ ‫مﺌة‬ ‫توزيع‬ ‫يبﻦﻴ‬ ‫الذي‬ ‫التاﱄ‬ ‫الجدول‬ ‫من‬ ‫الحسايب‬ ‫الوسﻂ‬ ‫احسب‬
. ‫ام‬‫ر‬‫ﻏ‬ ‫بالكيلو‬ ‫الوزن‬ ‫فﺌات‬
‫فﺌة‬ ‫كل‬ ‫مركز‬ ‫نوجد‬ / ‫الحـــل‬
35 = = = ‫األوﱃ‬ ‫الفﺌة‬ ‫مركز‬
45 = = = ‫الثانية‬ ‫الفﺌة‬ ‫مركز‬
: ‫هي‬ ‫الحل‬ ‫خطوات‬ ‫فﺈن‬ ‫وبالتاﱄ‬
. (x) ‫بالرمز‬ ‫لها‬ ‫ونرمز‬ ‫الفﺌات‬ ‫اكز‬‫ر‬‫م‬ ‫حساب‬ -1
. (f) ‫ارها‬‫ر‬‫تك‬ ‫يف‬ (x) ‫فﺌة‬ ‫مركز‬ ‫نﴬب‬ -2
40 + 30
22
70
7 ‫مثال‬
: ‫الفﺌات‬ ‫ذي‬ ‫اري‬‫ر‬‫التك‬ ‫للتوزيع‬ ‫الحسايب‬ ‫الوسﻂ‬ [5 -4-2]
‫الوزن‬ ‫فﺌات‬‫االشخاص‬ ‫عدد‬
30-9
40-15
50-22
60-25
70-18
80 - 9011
100 ‫املجموع‬
50 + 40
22
90

87. 87
‫العالقة‬ ‫من‬ ‫الحسايب‬ ‫الوسﻂ‬ ‫نوجد‬ -3
x =
x=
‫ام‬‫ر‬‫ﻏ‬ ‫كيلو‬ 61.1 =
: ‫اﻵﻲﺗ‬ ‫اري‬‫ر‬‫التك‬ ‫الجدول‬ ‫من‬ ‫الحسايب‬ ‫الوسﻂ‬ ‫جد‬
x.ff ‫اﻟﺘﻜﺮار‬‫اﻟﻔﺌﺎت‬ ‫ﻣﺮﻛﺰ‬
(x)
‫اﻟﻮزن‬ ‫ﻓﺌﺎت‬
31593530-
675154540-
1210225550-
1625256560-
1350187570-
935118580-90
6110100
6110
100
8 ‫مثال‬
‫الفﺌات‬8-10-12-14-16-18-
‫ار‬‫ر‬‫التك‬51520106460 ‫املجموع‬
x i
f i
fi
∑
∑
∑f= ∑xf=

88. 88
x = / ‫الحــــل‬
x =
x= 13.3
. ‫الحسابية‬ ‫العمليات‬ ‫يف‬ ‫والبساﻃة‬ ‫بالسهولة‬ ‫ﻤﻳتاز‬ (1)
. ‫حسابه‬ ‫يف‬ ‫القيم‬ ‫جميع‬ ‫تدخل‬ (2)
‫بالنسبة‬ ً‫ا‬‫جد‬ ‫صﻐرية‬ ‫أو‬ ً‫ا‬‫جد‬ ‫كبرية‬ ‫تكون‬ ‫التي‬ ‫وهي‬ ‫املتطرفة‬ ‫أو‬ ‫الﺸاذة‬ ‫بالقيم‬ ‫يتأثر‬ (1)
. ‫القيم‬ ‫معظم‬ ‫عن‬ ‫قيمته‬ ‫تخفض‬ ‫او‬ ‫الوسﻂ‬ ‫قيمة‬ ‫ترفع‬ ‫فهي‬ ‫وبالتاﱄ‬ ‫القيم‬ ‫ملعظم‬
. ً‫ا‬‫بياني‬ ‫أيجاده‬ ‫الﻤﻳكن‬ (2)
x . f‫ار‬‫ر‬‫التك‬
f
‫الفﺌات‬ ‫مركز‬
(x)
‫الوزن‬ ‫فﺌات‬
9×5 =45598-
11×15=165151110-
13×20=260201312-
15×10=150101514-
17×6=10261716-
19×4=7641918-
79860
798
60
: ‫الحسايب‬ ‫الوسﻂ‬ ‫ايا‬‫ز‬‫م‬
: ‫العيوب‬
x i
f i
fi
∑
∑
∑fx=∑f=

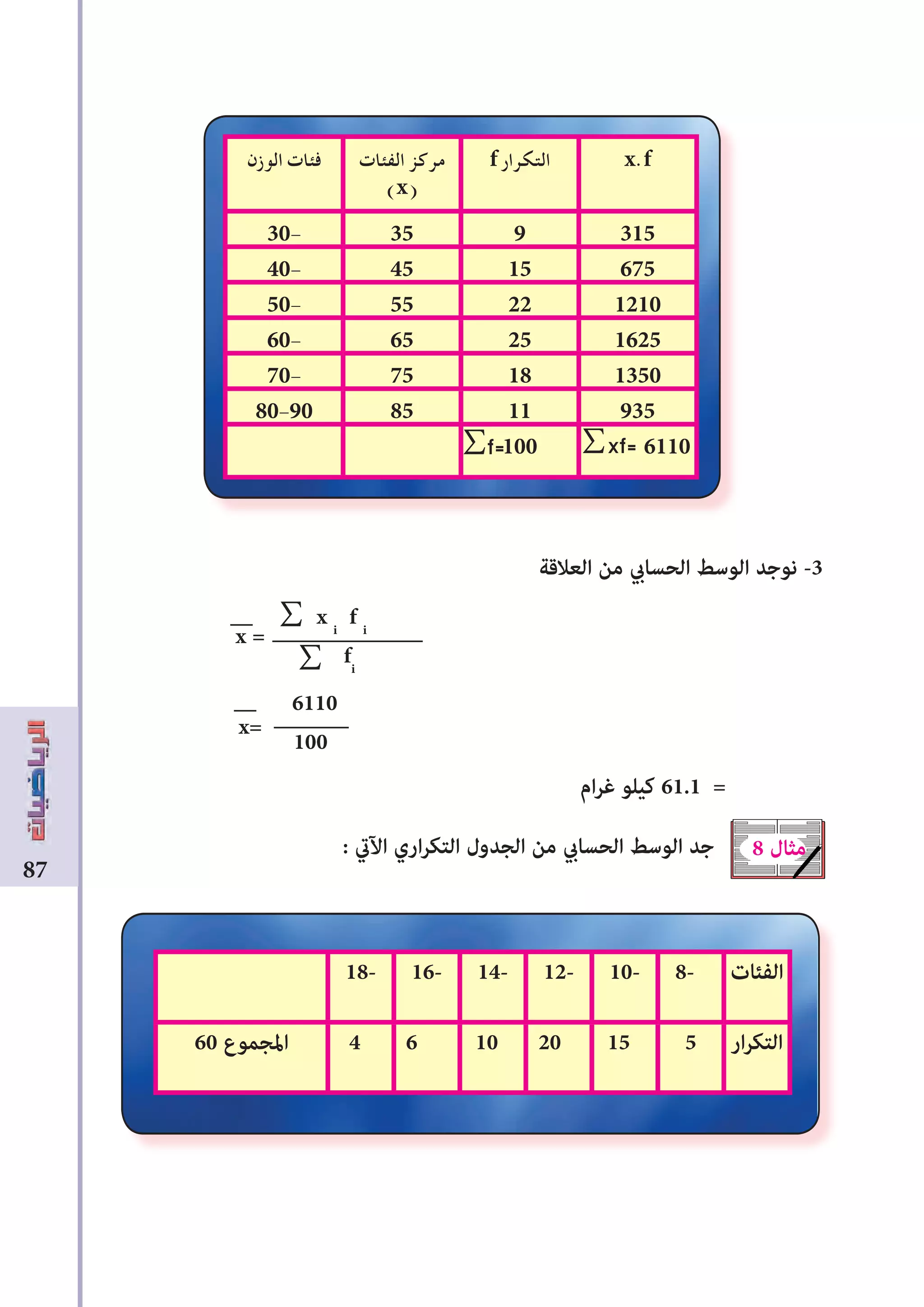
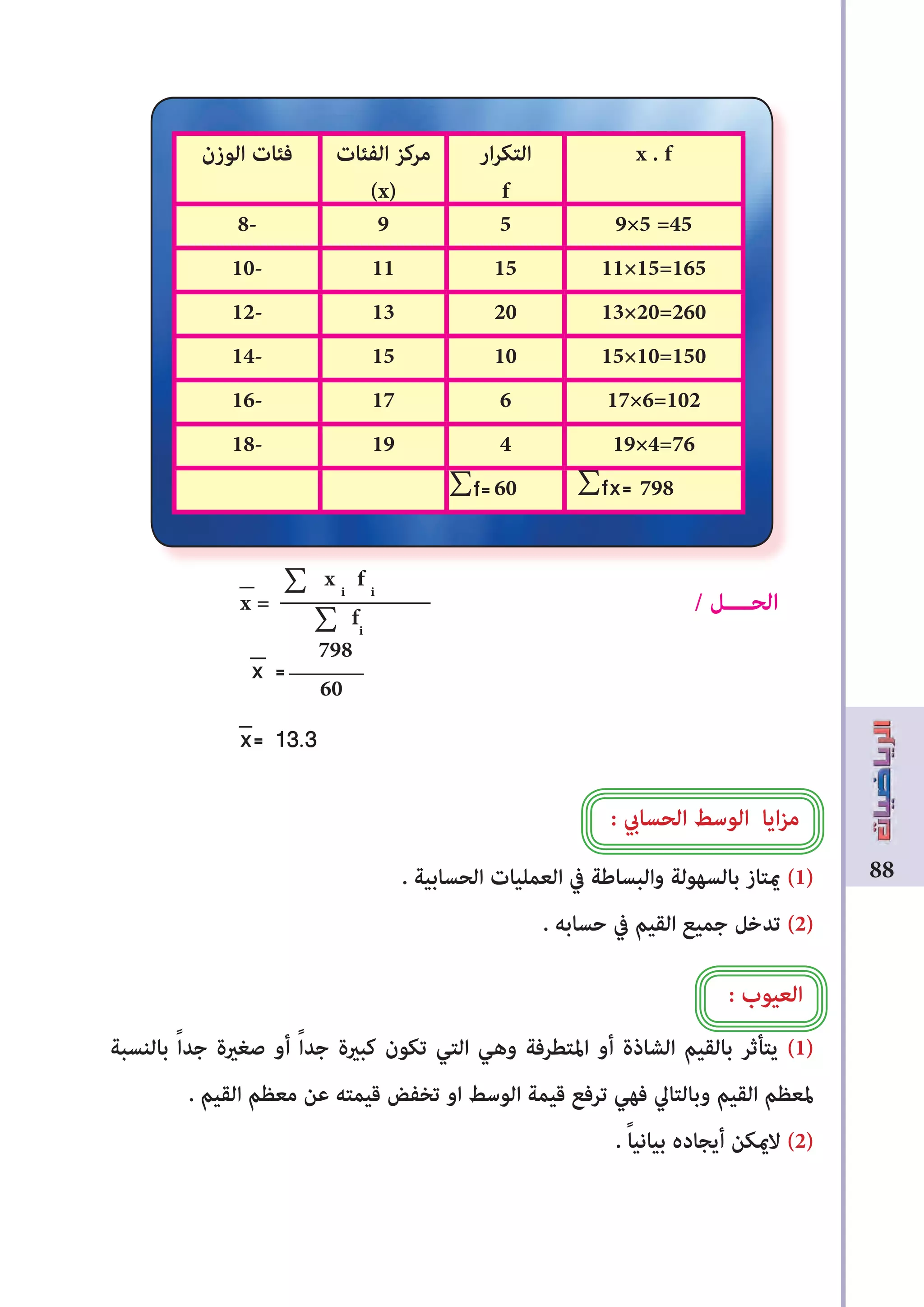
89. 89
: ‫الوسيﻂ‬ [5-5]Median
‫املجموعة‬ ‫تتوسﻂ‬ ‫التي‬ ‫القيمة‬ ‫إنه‬ ‫القيم‬ ‫من‬ ‫ملجموعة‬ ‫الوسيﻂ‬ ‫يعرف‬
‫يكون‬ ‫منه‬ ‫األصﻐر‬ ‫القيم‬ ‫عدد‬ ‫فﺈن‬ ‫وبالتاﱄ‬ ً‫ا‬‫تنازلي‬ ‫أو‬ ً‫ا‬‫تصاعدي‬ ‫ترتيبها‬ ‫بعد‬
. ‫منه‬ ‫االكﱪ‬ ‫القيم‬ ‫لعدد‬ ً‫ا‬‫مساوي‬
: ‫الوسيﻂ‬ ‫حساب‬ ‫ﻃريقة‬
: ‫املبوبة‬ ‫ﻏري‬ ‫البيانات‬ ‫يف‬ / ً‫ال‬‫أو‬
‫هي‬ ‫لتكون‬ ‫املنتصﻒ‬ ‫يف‬ ‫تقع‬ ‫التي‬ ‫القيمة‬ ‫نأخذ‬ ‫ثم‬ ً‫ا‬‫تنازلي‬ ‫أو‬ ً‫ا‬‫تصاعدي‬ ً‫ا‬‫ترتيب‬ ‫القيم‬ ‫نرتب‬
‫اللتﻦﻴ‬ ‫القيمتﻦﻴ‬ ‫فنأخذ‬ ً‫ا‬‫زوجي‬ ‫القيم‬ ‫عدد‬ ‫كان‬ ‫إذا‬ ‫اما‬ . ً‫ا‬‫فردي‬ ‫القيم‬ ‫عدد‬ ‫كان‬ ‫اذا‬ ‫هذا‬ . ‫الوسيﻂ‬
. (2) ‫عىل‬ ً‫ا‬‫مقسوم‬ ‫القيمتﻦﻴ‬ ‫مجموع‬ ‫هو‬ ‫الوسيﻂ‬ ‫ويكون‬ ‫املنتصﻒ‬ ‫يف‬
: ‫ام‬‫ر‬‫ﻏ‬ ‫بالكيلو‬ ‫التالية‬ ‫الطالب‬ ‫ان‬‫ز‬‫ألو‬ ‫الوسيﻂ‬ ‫احسب‬
55 , 63 , 50 , 58 , 52
50,51,55,58,63 : ً‫ا‬‫تصاعدي‬ ‫القيم‬ ‫نرتب‬ / ‫الحــل‬
. ‫الرتتيب‬ ‫يف‬ ‫الثالثة‬ ‫هي‬ ‫املنتصﻒ‬ ‫يف‬ ‫التي‬ ‫القيمة‬ ‫أن‬ ‫نالحﻆ‬
55 = ‫الوسيﻂ‬ ‫قيمة‬ ∴
: ( 5 - 2 ) ‫تعريﻒ‬
9 ‫مثال‬

90. 90
: ‫ام‬‫ر‬‫ﻏ‬ ‫بالكيلو‬ ‫التالية‬ ‫الطالب‬ ‫ان‬‫ز‬‫ألو‬ ‫الوسيﻂ‬ ‫احسب‬
55 , 57 , 63 , 50 ,58 , 25
‫نالحﻆ‬ 50,53,55,57,58,63 ً‫ا‬‫تصاعدي‬ ‫القيم‬ ‫نرتب‬ / ‫الحــل‬
: ‫كاﻵﻲﺗ‬ ‫الرتتيب‬ ‫ويكون‬ ‫املنتصﻒ‬ ‫يف‬ ‫قيمتﻦﻴ‬ ‫وجود‬
: ‫أن‬ ‫أي‬ + 1 ‫والثانية‬ ‫األوﱃ‬
3 = = ‫األول‬ ‫ترتيب‬
4 = 1 + 3 = + 1 = ‫الثاين‬ ‫وترتيب‬
. ‫ابعة‬‫ر‬‫وال‬ ‫الثالثة‬ ‫القيمتﻦﻴ‬ ‫بﻦﻴ‬ ‫تنحﴫ‬ ‫الوسيﻂ‬ ‫قيمة‬ ‫أن‬ ‫أي‬
= ‫الوسيﻂ‬ ‫قيمة‬ ∴
56 = =
: ‫املبوبة‬ ‫البيانات‬ ‫يف‬ / ً‫ا‬‫ثاني‬
‫الخطوات‬ ‫وحسب‬ ً‫ا‬‫حسابي‬ ‫الفﺌات‬ ‫ذات‬ ‫املبوبة‬ ‫البيانات‬ ‫حالة‬ ‫يف‬ ‫الوسيﻂ‬ ‫حساب‬ ‫ﻤﻳكن‬
: ‫اﻵتية‬
. ‫اري‬‫ر‬‫التك‬ ‫الجدول‬ ‫من‬ ‫الصاعد‬ ‫املتجمع‬ ‫ار‬‫ر‬‫التك‬ ‫جدول‬ ‫نكون‬ (1)
= ‫وهو‬ ‫الوسيﻂ‬ ‫ترتيب‬ ‫حساب‬ (2)
‫الصاعد‬ ‫املتجمع‬ ‫اري‬‫ر‬‫التك‬ ‫الجدول‬ ‫من‬ ‫الوسيﻂ‬ ‫عىل‬ ‫تحتوي‬ ‫التي‬ ‫الفﺌة‬ ‫تحديد‬ (3)
‫ترتيب‬ ‫يساوي‬ ‫أو‬ ‫أكﱪ‬ ‫ار‬‫ر‬‫تك‬ ‫أول‬ ‫تقابل‬ ‫التي‬ ‫الفﺌة‬ ‫وهي‬ ‫الوسيطية‬ ‫الفﺌة‬ ‫وتسمﻰ‬
. ‫الوسيﻂ‬
2
n
57 + 55
2
10 ‫مثال‬
2
n
2
6
2
6
2
112
‫ارت‬‫ر‬‫التك‬ ‫مجموع‬
2

91. 91
= ‫اﻟﻮﺳﻴﻂ‬ ‫ﻗﻴﻤﺔ‬ (4)
‫اﻟﻔﺌﺔ‬ ‫ﻃﻮل‬ × + ‫اﻟﻮﺳﻴﻄﻴﺔ‬ ‫ﻟﻠﻔﺌﺔ‬ ‫اﻷدﻰﻧ‬ ‫اﻟﺤﺪ‬
ME= L+ × W : ‫ﺑﺎﻟﺮﻣﻮز‬
. ‫اﻟﻮﺳﻴﻄﻴﺔ‬ ‫ﻗﺒﻞ‬ ‫ﻟﻠﻔﺌﺔ‬ ‫اﻟﺼﺎﻋﺪ‬ ‫اﳌﺘﺠﻤﻊ‬ ‫ار‬‫ﺮ‬‫اﻟﺘﻜ‬ = fb
‫ﺣﻴﺚ‬
. ‫اﻟﻮﺳﻴﻄﻴﺔ‬ ‫اﻟﻔﺌﺔ‬ ‫ار‬‫ﺮ‬‫ﺗﻜ‬ = fm
. ‫ار‬‫ﺮ‬‫اﻟﺘﻜ‬ = f
. ‫اﻟﻔﺌﺔ‬ ‫ﻃﻮل‬ = w
. ‫اﻟﻮﺳﻴﻂ‬ = ME
‫اﻟﻮﺳﻴﻄﺔ‬ ‫ﻟﻠﻔﺌﺔ‬ ‫اﻻدﻰﻧ‬ ‫اﻟﺤﺪ‬ =L
: ‫اﻟﺘﺎﱄ‬ ‫اﻟﺠﺪول‬ ‫ﻣﻦ‬ ‫اﻟﻮزن‬ ‫وﺳﻴﻂ‬ ‫ﺟﺪ‬
‫اﻟﻮﺳﻴﻄﻴﺔ‬ ‫ﻗﺒﻞ‬ ‫ﻟﻠﻔﺌﺔ‬ ‫اﳌﺘﺠﻤﻊ‬ ‫ار‬‫ﺮ‬‫اﻟﺘﻜ‬ - ‫اﻟﻮﺳﻴﻂ‬ ‫ﺗﺮﺗﻴﺐ‬
‫اﻟﻮﺳﻴﻄﻴﺔ‬ ‫اﻟﻔﺌﺔ‬ ‫ار‬‫ﺮ‬‫ﺗﻜ‬
11 ‫ﻣﺜﺎل‬
‫اﻟﻮزن‬ ‫ﻓﺌﺎت‬‫اﻻﺷﺨﺎص‬ ‫ﻋﺪد‬ ‫ار‬‫ﺮ‬‫ﺗﻜ‬‫اﻟﺼﺎﻋﺪ‬ ‫اﳌﺘﺠﻤﻊ‬ ‫ار‬‫ﺮ‬‫اﻟﺘﻜ‬
30 -99
40 -1524
50 -2246
60 -2571
70 -1889
80 - 9011100
100 ‫اﳌﺠﻤﻮع‬
f -fb
fm
2
∑

92. 92
/ ‫الحــل‬
50 = = ‫الوسيﻂ‬ ‫ترتيب‬
ME= L+ × W
70 - 60 ‫هي‬ ‫الوسيطية‬ ‫الفﺌة‬
ME= 60+ × 10
= 60 +
= 60 + 1.6
ME= 61.6
. ‫املتطرفة‬ ‫أو‬ ‫الﺸاذة‬ ‫بالقيم‬ ‫يتأثر‬ ‫ال‬ (1)
. ً‫ا‬‫بياني‬ ‫ايجاده‬ ‫ﻤﻳكن‬ (2)
. ‫حسابه‬ ‫يف‬ ‫القيم‬ ‫جميع‬ ‫تدخل‬ ‫ال‬ (1)
. ‫حسابه‬ ‫يف‬ ‫تقريبية‬ ‫ﻃرق‬ ‫تستخدم‬ ‫الفﺌات‬ ‫ذات‬ ‫املبوبة‬ ‫البيانات‬ ‫حالة‬ ‫يف‬ (2)
100
2
50 - 46
25
40
25
: ‫الوسيﻂ‬ ‫ايا‬‫ز‬‫م‬
: ‫العيوب‬
f -fb
fm
2
∑

93. 93
: ‫املـنــوال‬ [5-6]
: ( 5 - 3 ) ‫تعريﻒ‬
12 ‫مثال‬
d1
d1
+d2
‫فﺌات‬‫ار‬‫ر‬‫التك‬
30 -9
40 -15
50 -22
60 -25
70 -18
80 - 9011
‫السابق‬ ‫ار‬‫ر‬‫التك‬ ⇐
‫املنواﱄ‬ ‫ار‬‫ر‬‫التك‬ ⇐
‫الالحق‬ ‫ار‬‫ر‬‫التك‬ ⇐
13 ‫مثال‬
Mode
‫تقابل‬ ‫التي‬ ‫أو‬ ً‫ا‬‫ر‬‫ا‬‫ر‬‫تك‬ ‫األكرث‬ ‫القيمة‬ ‫أنه‬ ‫القيم‬ ‫من‬ ‫ملجموعة‬ ‫املنوال‬ ‫يعرف‬
.MO ‫له‬ ‫ويرمز‬ ‫ات‬‫ر‬‫ا‬‫ر‬‫التك‬ ‫أكﱪ‬
4 , 2 , 4 , 8 , 3 , 4 , 9 , 7 , 4 : ‫اﻵتية‬ ‫األعداد‬ ‫ملجموعة‬ ‫املنوالية‬ ‫القيمة‬ ‫ما‬
. ‫ﻏريها‬ ‫من‬ ‫اكرث‬ ‫تكررت‬ ‫ألنها‬ 4 = ‫املنوالية‬ ‫القيمة‬ / ‫الحــل‬
‫الفﺌات‬ ‫ذات‬ ‫املبوبة‬ ‫البيانات‬ ‫يف‬ ‫املنوال‬ ‫لحساب‬ ‫الفروق‬ ‫ﻃريقة‬
‫املنوالية‬ ‫الفﺌة‬ ‫ﻃول‬ × + ‫املنوالية‬ ‫للفﺌة‬ ‫األدين‬ ‫الحد‬ = ‫املنوال‬
. ‫له‬ ‫السابق‬ ‫ار‬‫ر‬‫والتك‬ ‫املنواﱄ‬ ‫ار‬‫ر‬‫التك‬ ‫بﻦﻴ‬ ‫الفرق‬ = d1
‫حيث‬
. ‫الالحق‬ ‫ار‬‫ر‬‫والتك‬ ‫املنواﱄ‬ ‫ار‬‫ر‬‫التك‬ ‫بﻦﻴ‬ ‫الفرق‬ = d2
‫تقابل‬ ‫التي‬ ‫املنوالية‬ ‫والفﺌة‬ . ‫الجدول‬ ‫يف‬ ‫ار‬‫ر‬‫تك‬ ‫اكﱪ‬ ‫هو‬ ‫املنواﱄ‬ ‫ار‬‫ر‬‫التك‬ ‫وان‬
. ‫ار‬‫ر‬‫تك‬ ‫اكﱪ‬
‫الجدول‬ ‫من‬ ‫املنوال‬ ‫احسب‬

94. 94
/ ‫الحــل‬
d1
= 25 - 22 = 3
d2
= 25 - 18 = 7
70 - 60 = 10 ‫املنوالية‬ ‫الفﺌة‬ ‫ﻃول‬
‫املنوالية‬ ‫الفﺌة‬ ‫ﻃول‬ × + ‫املنوالية‬ ‫للفﺌة‬ ‫األدين‬ ‫الحد‬ = ‫املنوال‬
MO= 60 + × 10
= 60 + × 10
= 60 +3
MO= 63 ‫املنوال‬
. ‫إيجاده‬ ‫ﻃريقة‬ ‫أو‬ ‫الفكرة‬ ‫حيث‬ ‫من‬ ‫بسيﻂ‬ (1)
. ‫املتطرفة‬ ‫أو‬ ‫الﺸاذة‬ ‫بالقيم‬ ‫يتأثر‬ ‫ال‬ (2)
‫ذات‬ ‫املبوبة‬ ‫البيانات‬ ‫حالة‬ ‫يف‬ ‫سيﺎﻤ‬ ‫ال‬ ‫تقريبية‬ ‫ﻃرق‬ ‫أنها‬ ‫اال‬ ‫حسابه‬ ‫ﻃرق‬ ‫تعدد‬ ‫رﻏم‬ (1)
. ‫الفﺌات‬
‫للقيم‬ ‫منوال‬ ‫يوجد‬ ‫ال‬ ‫اي‬ ، ‫املنوال‬ ‫ايجاد‬ ‫ﻤﻳكن‬ ‫ال‬ ‫التعريﻒ‬ ‫وحسب‬ ‫الحاالت‬ ‫بعض‬ ‫يف‬ (2)
‫من‬ ‫أكرث‬ ‫يوجد‬ ‫األخرى‬ ‫الحاالت‬ ‫بعض‬ ‫ويف‬ (‫ﻏريها‬ ‫من‬ ‫اكرث‬ ‫متكررة‬ ‫قيمة‬ ‫توجد‬ ‫ﻢﻟ‬ ‫)اذا‬
.(‫القيم‬ ‫باقي‬ ‫من‬ ‫واكرث‬ ‫نفسها‬ ‫بالدرجة‬ ‫القيم‬ ‫ار‬‫ر‬‫تك‬ ‫حالة‬ ‫يف‬ ‫)كﺎﻤ‬ ‫منوال‬
: ‫املنوال‬ ‫ايا‬‫ز‬‫م‬
: ‫العيوب‬
3 + 7
3
3
10
d1
d1
+d2

95. 95
: ‫الطالب‬ ‫من‬ ‫مجموعة‬ ‫أعﺎﻤر‬ ‫متثل‬ ‫التالية‬ ‫البيانات‬ (1
. 19 , 17 , 18 , 17 , 15 , 18 , 16 , 17 , 15
: ‫يأﻲﺗ‬ ‫مﺎﻤ‬ ‫كل‬ ‫جد‬
‫املنوال‬ (‫جـ‬ ‫الوسيﻂ‬ ( ‫ب‬ ‫الحسايب‬ ‫الوسﻂ‬ (‫أ‬
‫الرياضيات‬ ‫مبادة‬ ‫الصفوف‬ ‫أحد‬ ‫يف‬ ‫الطالب‬ ‫لدرجات‬ ‫الحسايب‬ ‫الوسﻂ‬ ‫أن‬ ‫فرضنا‬ ‫إذا‬ (2
‫عدد‬ ‫أن‬ ‫فرضنا‬ ‫وإذا‬ . ‫درجة‬ (75) ‫قبله‬ ‫الذي‬ ‫العام‬ ‫ويف‬ ‫درجة‬ (80) ‫هي‬ ‫املاﴈ‬ ‫للعام‬
. ً‫ا‬‫ﻃالب‬ (15) ‫قبله‬ ‫الذي‬ ‫العام‬ ‫ويف‬ ‫ﻃالبا‬ (20) ‫املاﴈ‬ ‫العام‬ ‫يف‬ ‫الصﻒ‬ ‫ﻃالب‬
. ‫العامﻦﻴ‬ ‫يف‬ ‫الطالب‬ ‫لدرجات‬ ‫الحسايب‬ ‫الوسﻂ‬ ‫احسب‬
‫فصل‬ ‫يف‬ ً‫ا‬‫يوم‬ 90 ‫خالل‬ ‫املدن‬ ‫إحدى‬ ‫يف‬ ‫ارة‬‫ر‬‫الح‬ ‫درجات‬ ‫توزيع‬ ‫يبﻦﻴ‬ ‫التاﱄ‬ ‫الجدول‬ (3
. ‫األعوام‬ ‫احد‬ ‫يف‬ ‫الصيﻒ‬
. ‫ارة‬‫ر‬‫الح‬ ‫لدرجات‬ ‫الحسايب‬ ‫الوسﻂ‬ ‫قيمة‬ ‫حساب‬ ( ‫أ‬
. ‫الوسيﻂ‬ ‫قيمة‬ ‫حساب‬ (‫ب‬
. ‫املنوال‬ ‫قيمة‬ ‫حساب‬ ( ‫جـ‬
‫درجات‬ ‫فﺌات‬
‫ارة‬‫ر‬‫الح‬
20-24-28-32-36-40-48 - 44‫املجموع‬
‫األيام‬ ‫عدد‬8101823159790
(5-1) ‫متارين‬

96. 96
Measures of Varedtion
‫تكون‬ ‫رمبا‬ ‫املجموعة‬ ‫هذه‬ ‫اعداد‬ ‫وأن‬ ً‫ا‬‫حسابي‬ ً‫ا‬‫وسط‬ ‫األعداد‬ ‫من‬ ‫مجموعة‬ ‫لكل‬ ‫ان‬
‫وسطها‬ ‫من‬ ‫بالقرب‬ ‫متجمعة‬ ‫األعداد‬ ‫هذه‬ ‫كانﺖ‬ ‫فﺈذا‬ ، ‫عنه‬ ‫مبتعدة‬ ‫أو‬ ‫منه‬ ‫بالقرب‬ ‫متجمعة‬
‫الحسايب‬ ‫وسطها‬ ‫عن‬ ‫مبتعدة‬ ‫األعداد‬ ‫هذه‬ ‫كانﺖ‬ ‫واذا‬ ، ‫ضﺌيل‬ ‫تﺸتتها‬ ‫مقدار‬ ‫فﺈن‬ ، ‫الحسايب‬
.‫كبري‬ ‫تﺸتتها‬ ‫فﺈن‬
50 ‫هو‬ 70 , 60 , 50 , 40 , 30 ‫لﻸعداد‬ ‫الحسايب‬ ‫الوسﻂ‬ ‫إن‬
55 ‫هو‬ 100 , 90 , 20 , 10 ‫لﻸعداد‬ ‫الحسايب‬ ‫والوسﻂ‬
‫تﺸتﺖ‬ ‫بينﺎﻤ‬ ، ‫ضﺌيل‬ ‫الحسايب‬ ‫الوسﻂ‬ ‫عن‬ ‫تﺸتتها‬ ‫ان‬ ‫تﺸاهد‬ ‫األوﱃ‬ ‫املجموعة‬ ‫أعداد‬ ‫تأمل‬ ‫عند‬
. ‫كبري‬ ‫الحسايب‬ ‫الوسﻂ‬ ‫عن‬ ‫الثانية‬ ‫املجموعة‬ ‫أعداد‬
‫التﺸتﺖ‬ ‫مقاييس‬
: ‫هي‬ ‫ندرسها‬ ‫سوف‬ ‫التي‬ ‫التﺸتﺖ‬ ‫مقاييس‬ ‫ان‬
. ‫املدى‬ -1
. ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ -2
Range
. 1 + ‫للمتﻐري‬ ‫قيمة‬ ‫واصﻐر‬ ‫قيمة‬ ‫اكﱪ‬ ‫بﻦﻴ‬ ‫الفرق‬ ‫هو‬ : ‫املدى‬
‫اقل‬ ‫وهﺎﻤ‬ ، ‫املتﻐري‬ ‫قيم‬ ‫من‬ ‫فقﻂ‬ ‫قيمتﻦﻴ‬ ‫عىل‬ ‫يتوقﻒ‬ ‫ألنه‬ ، ‫للتﺸتﺖ‬ ً‫ا‬‫هام‬ ً‫ا‬‫مقياس‬ ‫ليس‬ ‫واملدى‬
‫وان‬ . ‫العينة‬ ‫بذبذبات‬ ً‫ا‬‫بالﻐ‬ ً‫ا‬‫ر‬‫تأث‬ ‫يتأثر‬ ‫فهو‬ ‫ولذا‬ ‫للمتﻐري‬ ‫قيمة‬ ‫واكﱪ‬ ‫قيمة‬
. ‫املدى‬ ‫قيمة‬ ‫يف‬ ‫بوضوح‬ ‫يؤثر‬ ‫القيمتﻦﻴ‬ ‫هاتﻦﻴ‬ ‫من‬ ‫أي‬ ‫يف‬ ‫يحدث‬ ‫تﻐري‬ ‫أي‬
: ‫التﺸتﺖ‬ ‫مقاييس‬ [5-7]
14 ‫مثال‬
: ‫املـــــدى‬ [ 5 - 7 - 1]

97. 97
98 , 24 , 68 , 35 , 12 ‫؟‬ ‫التالية‬ ‫القيم‬ ‫مجموعة‬ ‫يف‬ ‫املدى‬ ‫هو‬ ‫ما‬
‫املدى‬ = 98 - 12 + 1 = 87 / ‫الحــل‬
‫؟‬ ‫اﻵﻲﺗ‬ ‫اري‬‫ر‬‫التك‬ ‫التوزيع‬ ‫يف‬ ‫املدى‬ ‫هو‬ ‫ما‬
‫املدى‬ = 55 - 5 = 50 / ‫الحــل‬
Standard Deviation
‫من‬ ‫ن‬ ‫لدينا‬ ‫كانﺖ‬ ‫فﺈذا‬ . ‫استخداما‬ ‫التﺸتﺖ‬ ‫مقاييس‬ ‫اكرث‬ ‫من‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫يعد‬
‫من‬ ‫متقاربة‬ ‫تكون‬ ‫املفردات‬ ‫هذه‬ ‫فﺈن‬ . x ‫الحسايب‬ ‫ووسطها‬ x1
, x2
,...,xn : ‫املفردات‬
.‫صﻐرية‬ x ‫عن‬ ‫افاتها‬‫ر‬‫انح‬ ‫كانﺖ‬ ‫إذا‬ ‫اي‬ x ‫الحسايب‬ ‫وسطها‬ ‫من‬ ‫قريبة‬ ‫كانﺖ‬ ‫إذا‬ ‫البعض‬ ‫بعضها‬
، ‫التﺸتﺖ‬ ‫لقياس‬ ‫استخدامها‬ ‫ﻤﻳكن‬ ‫الحسايب‬ ‫وسطها‬ ‫عن‬ ‫املفردات‬ ‫افات‬‫ر‬‫انح‬ ‫فﺈن‬ ‫وبالتاﱄ‬
. ‫افات‬‫ر‬‫االنح‬ ‫هذه‬ ‫متوسﻂ‬ ‫باخذ‬ ‫ذلﻚ‬ ‫يتم‬ ‫ان‬ ‫وﻤﻳكن‬
‫ملتوسﻂ‬ ‫الرتبيعي‬ ‫للجذر‬ ‫املوجبة‬ ‫القيمة‬ ‫هو‬ : ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬
‫وسطها‬ ‫عن‬ ‫التوزيع‬ ‫مفردات‬ ‫قيم‬ ‫افات‬‫ر‬‫انح‬ ‫مربعات‬
. (S) ‫بالرمز‬ ‫له‬ ‫ويرمز‬ ‫الحسايب‬
: ( 5 - 4 ) ‫تعريﻒ‬
15 ‫مثال‬
16 ‫مثال‬
‫اﻟﻔﺌﺎت‬5-15-25-35-55 - 45
‫اﻟﺘﻜﺮار‬3815147
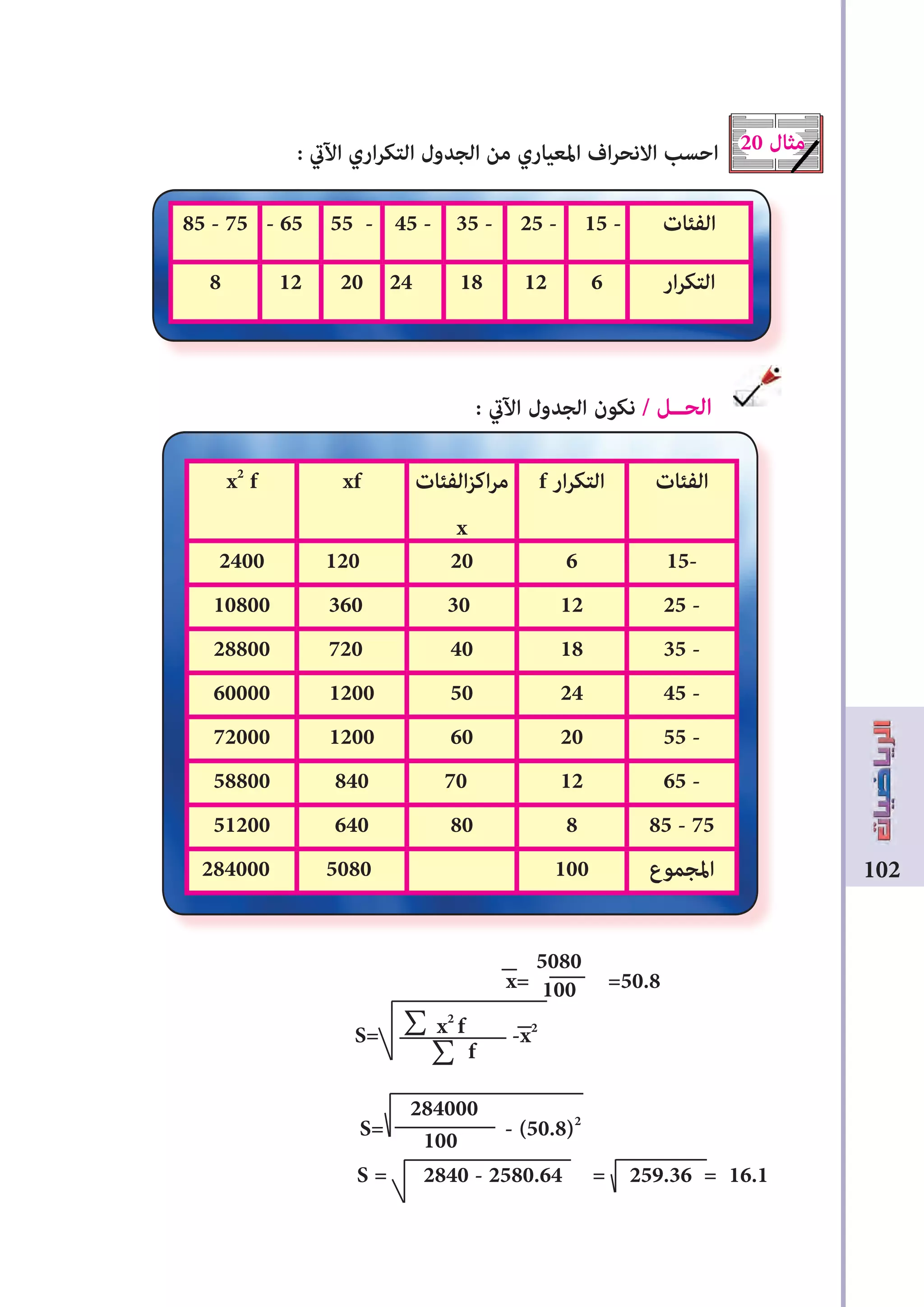
: ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ [ 5 - 7 - 2]

98. 98
: ‫اري‬‫ر‬‫تك‬ ‫توزيع‬ ‫يف‬ ‫او‬ ‫ارية‬‫ر‬‫التك‬ ‫ﻏري‬ ‫لقيم‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫حساب‬
. ‫القيم‬ ‫لتلﻚ‬ (x) ‫الحسايب‬ ‫الوسﻂ‬ ‫نستخرج‬ -1
. ( x - x ) ‫الحسايب‬ ‫وسطها‬ ‫عن‬ ‫قيمة‬ ‫كل‬ ‫اف‬‫ر‬‫انح‬ ‫نستخرج‬ -2
. ( x - x )2
‫افات‬‫ر‬‫االنح‬ ‫نربع‬ -3
. ( x - x )2
‫افات‬‫ر‬‫االنح‬ ‫مربعات‬ ‫نجمع‬ -4
‫القيم‬ ‫عدد‬ ‫عىل‬ ‫الناتﺞ‬ ‫نقسم‬ -5
. ‫األخري‬ ‫للناتﺞ‬ ‫املوجب‬ ‫الرتبيعي‬ ‫الجذر‬ ‫نأخذ‬ -6
S= ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫فيكون‬
‫او‬
S= -x 2
: ‫وهو‬ ‫استخدامه‬ ‫ﻤﻳكن‬ ‫آخر‬ ‫قانون‬ ‫فيوجد‬ ‫اري‬‫ر‬‫تك‬ ‫توزيع‬ ‫يف‬ ‫املتجمعة‬ ‫القيم‬ ‫يف‬ ‫أما‬ -7
S=
f x 2
-x 2
( x - x )2
n
( x - x )2
n
∑
∑
x2
n
∑
f
∑
∑

99. 99
: ‫اﻵتية‬ ‫للقيم‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫احسب‬
34 , 25 , 21 , 32 , 29 , 24 , 28 , 23
/ ‫الحـــل‬
x= = 27
s=
= = 18 = 3 2
= 3× 1.414 = 4.242
216
8
(x - x)2
(x -x)x
1623 - 27 = - 423
1128
9-324
4229
25532
36-621
4-225
49734
144216
17 ‫مثال‬
144
8
( x - x )2
n
∑x= ∑(x-x)2
=
∑

100. 100
9 ، 7 ، 5 ، 3 ، 1 : ‫التالية‬ ‫للبيانات‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫احسب‬
: (S) ‫ايجاد‬ ‫يف‬ ‫التاﱄ‬ ‫القانون‬ ‫نطبق‬ / ‫الحـــل‬
x= =5
S= -x 2
S= -25
S = 33 - 25 = 8 = 2 2
S = 2 × 1.414
S = 2.828 = 2.83
‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫اليجاد‬ S= ‫القانون‬ ‫استخدام‬ ‫تدريب‬
18 ‫مثال‬
25
5
165
5
x2
x
11
93
255
497
819
165 ‫املجموع‬25 ‫املجموع‬
x2
n
( x - x )2
n
∑
∑

101. 101
‫احسب‬ ‫ثم‬ (17) ‫املثال‬ ‫يف‬ ‫املوجودة‬ ‫القيم‬ ‫من‬ ‫قيمة‬ ‫كل‬ ‫من‬ (20) ‫اﻃرح‬
. ‫النتائﺞ‬ ‫وقارن‬ ‫الجديدة‬ ‫للقيم‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬
‫القيم‬ ‫تصبﺢ‬ ‫قيمة‬ ‫كل‬ ‫من‬ (20) ‫ﻃرح‬ ‫بعد‬ / ‫الحــل‬
14 , 5 , 1 , 12 , 9 , 8 , 3
x = = 7
S= -x 2
S = -49
S= 67 - 49 = 18 = 3 2
= 3 × 1.414 = 4.242
‫هذا‬ ‫ومن‬ ‫متساوية‬ ‫فيهﺎﻤ‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫قيمة‬ ‫أن‬ (19) , (17) ‫املثالﻦﻴ‬ ‫من‬ ‫يالحﻆ‬
. ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫قيمة‬ ‫عىل‬ ‫تؤثر‬ ‫ال‬ ‫القيم‬ ‫جميع‬ ‫من‬ ‫ثابتة‬ ‫كمية‬ ‫ﻃرح‬ ‫أن‬ ‫نستنتﺞ‬
19 ‫مثال‬
x= 561451129483x
x2
=5361962511448116649x2
56
8
x2
n
536
8
∑
∑
∑

102. 102
: ‫اﻵﻲﺗ‬ ‫اري‬‫ر‬‫التك‬ ‫الجدول‬ ‫من‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫احسب‬
: ‫اﻵﻲﺗ‬ ‫الجدول‬ ‫نكون‬ / ‫الحــل‬
x= =50.8
S= -x2
S= - (50.8)2
S = 2840 - 2580.64 = 259.36 = 16.1
20 ‫مثال‬
‫الفﺌات‬15 -25 -35 -45 -55 -- 6585 - 75
‫ار‬‫ر‬‫التك‬612182420128
‫الفﺌات‬f ‫ار‬‫ر‬‫التك‬‫الفﺌات‬‫ز‬‫اك‬‫ر‬‫م‬
x
xfx2
f
15-6201202400
25 -123036010800
35 -184072028800
45 -2450120060000
55 -2060120072000
65 -127084058800
85 - 7588064051200
‫املجموع‬1005080284000
284000
100
5080
100
x2
f
f
∑
∑

103. 103
: ‫األشخاص‬ ‫من‬ ‫مجموعة‬ ‫ألعﺎﻤر‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫احسب‬
/ ‫الحــل‬
S = - ( )2
S = 165.2174 = 12.85 ً‫ا‬‫تقريب‬
x f x f x2
f
17 3 51 867
27 5 135 3645
37 8 296 10952
47 4 188 8836
57 2 114 6498
67 1 67 4489
23 851 35287
72-62 52 - 42 - 32 - 22 - 12 - ‫العمر‬ ‫فﺌة‬
1 2 4 8 5 3 ‫االشخاص‬ ‫عدد‬
21 ‫مثال‬
35287
23
851
23
∑f= ∑xf= ∑x2
f=

104. 104
. 3 ,0 , 8 ,7 , 9 , 12 ‫التالية‬ ‫للقيم‬ ‫املدى‬ ‫أوجد‬ - 1
. ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫عرف‬ - 2
. 10 , 8 , 6 , 4 , 2 : ‫التالية‬ ‫للقيم‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫احسب‬ - 3
S= 2.83 ‫الجواب‬
. ‫انهم‬‫ز‬‫أو‬ ‫حسب‬ ‫الطالب‬ ‫من‬ ‫مجموعة‬ ‫توزيع‬ ‫يبﻦﻴ‬ ‫التاﱄ‬ ‫الجدول‬ - 4
. ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫احسب‬
S= 2.44 ‫الجواب‬
5 , 7 1 , 2 , 6 , 3 : ‫اﻵتية‬ ‫األعداد‬ ‫من‬ ‫كل‬ ‫إﱃ‬ (5) ‫العدد‬ ‫اضﻒ‬ - 5
‫عىل‬ ‫تؤثر‬ ‫ولكنها‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ ‫قيمة‬ ‫عىل‬ ‫تؤثر‬ ‫ال‬ ‫االضافة‬ ‫هذه‬ ‫ان‬ ‫اثبﺖ‬ ‫ثم‬
. ‫الحسايب‬ ‫الوسﻂ‬ ‫قيمة‬
‫الفﺌات‬- 2022 -24 -26 -28 -32 - 30
‫ار‬‫ر‬‫التك‬510201052
(5-2) ‫متارين‬

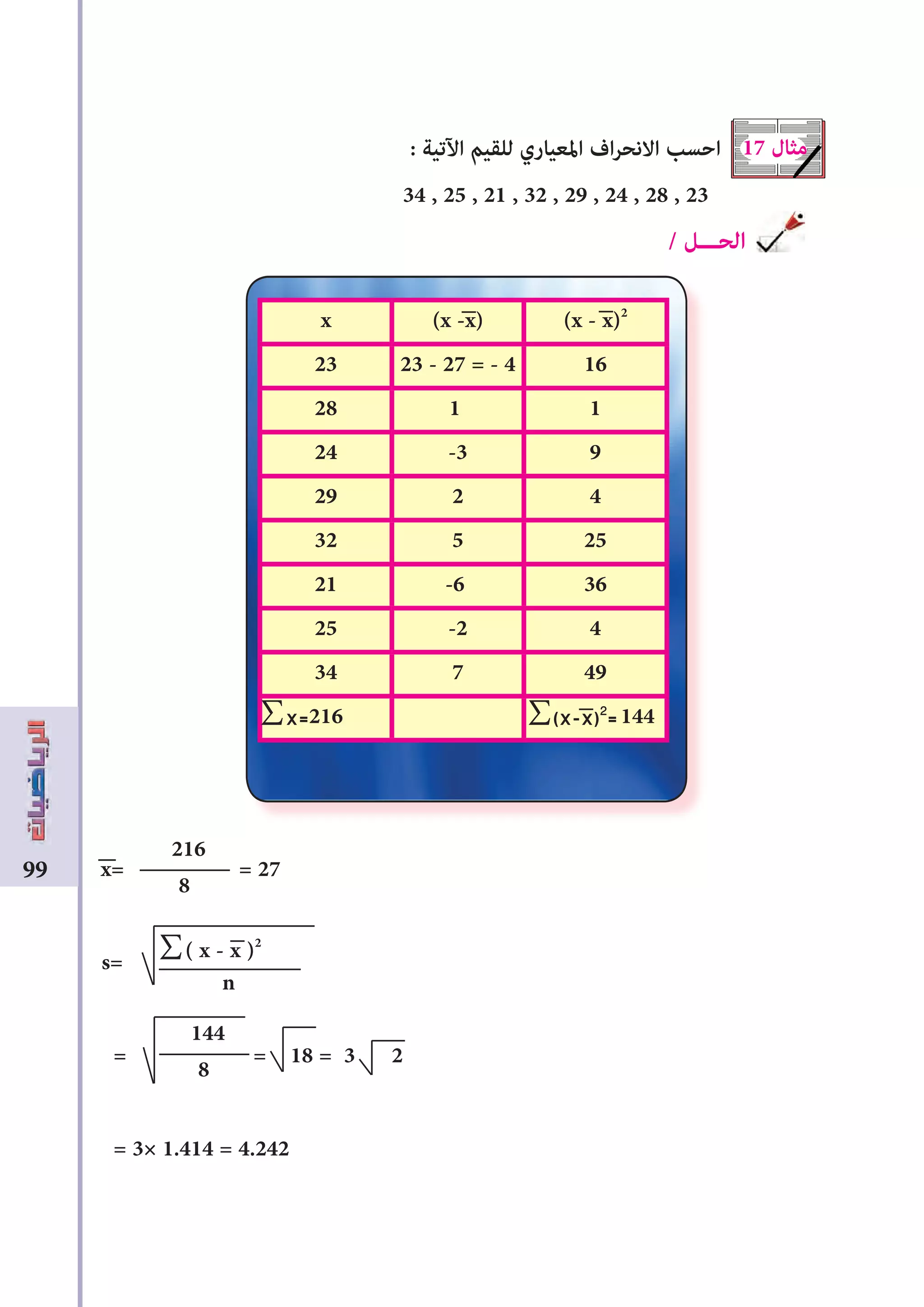
105. 105
: ‫األرتباط‬ [ 5 - 7 - 3 ]
: ( 5 - 5 ) ‫تعريﻒ‬
1
n (x-x ) (y- y )
Sx
Sy
∑
Correlation
‫أحدهﺎﻤ‬ ‫تﻐري‬ ‫اذا‬ ‫بحيث‬ ، ‫متﻐريين‬ ‫بﻦﻴ‬ ‫الرياضية‬ ‫العالقة‬ ‫هو‬ : ‫االرتباط‬
‫التﻐري‬ ‫كان‬ ‫فاذا‬ ً‫ا‬‫ايض‬ ‫معﻦﻴ‬ ‫اتجاه‬ ‫يف‬ ‫التﻐري‬ ‫إﱃ‬ ‫اﻵخر‬ ‫ﻤﻳيل‬ ‫معﻦﻴ‬ ‫باتجاه‬
‫باتجاهﻦﻴ‬ ‫كان‬ ‫اذا‬ ‫أما‬ ً‫ا‬‫ﻃردي‬ ‫االرتباط‬ ‫سمي‬ ‫واحد‬ ‫باتجاه‬ ‫الحالتﻦﻴ‬ ‫يف‬
.( r) ‫له‬ ‫ويرمز‬ ً‫ا‬‫عكسي‬ ‫التﻐري‬ ‫سمي‬ ‫متعاكسﻦﻴ‬
(‫)بريسون‬ ‫الخطي‬ ‫االرتباط‬ ‫معامل‬
‫ويرمز‬ ‫الخطي‬ ‫االرتباط‬ ‫معامل‬ ‫يسمﻰ‬ ‫مبقياس‬ ‫الظواهر‬ ‫بﻦﻴ‬ ‫االرتباط‬ ‫قوة‬ ‫تقاس‬
‫من‬ ( x1
, y1
),(x2
, y2
),...,(xn
, yn
) (‫القيم‬ ‫)أزواج‬ ‫من‬ n ‫لدينا‬ ‫كان‬ ‫فﺈذا‬ (r) ‫له‬
: ‫الصيﻐتﻦﻴ‬ ‫باحدى‬ ‫يحسب‬ (‫)بريسون‬ ‫الخطي‬ ‫االرتباط‬ ‫معامل‬ ‫فﺈن‬ (x) ,(y) ‫الظاهرتﻦﻴ‬
(1) r =
. x ‫للظاهرة‬ ‫الحسايب‬ ‫الوسﻂ‬ = x ‫أن‬ ‫حيث‬
. y ‫للظاهرة‬ ‫الحسايب‬ ‫الوسﻂ‬ = y
. x ‫للظاهرة‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ = S x
. y ‫للظاهرة‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ = Sy
(2) r =
1
n (x y )- (x y)
Sx
Sy
∑

106. 106
: ‫عىل‬ ‫الحصول‬ ‫يلزمنا‬ ‫االرتباط‬ ‫معامل‬ ‫لحساب‬ ‫ن‬َ‫أ‬ ‫اي‬
. x , y ‫الظاهرتﻦﻴ‬ ‫من‬ ‫لكل‬ ‫الحسايب‬ ‫الوسﻂ‬ - ‫أ‬
. ‫منهﺎﻤ‬ ‫لكل‬ ‫املعياري‬ ‫اف‬‫ر‬‫االنح‬ - ‫ب‬
x y ‫اي‬ ‫الظاهرتﻦﻴ‬ ‫من‬ ‫كل‬ ‫ﴐب‬ ‫حواصل‬ ‫مجموع‬ - ‫جـ‬
. ‫السابقتﻦﻴ‬ ‫القانونﻦﻴ‬ ‫احد‬ ‫يف‬ ‫والتعويض‬ (x - x) (y - y) ‫أو‬
‫االرتباط‬ ‫معامل‬ ‫خصائﺺ‬ ‫بعض‬
: ‫منها‬ ‫نذكر‬ ‫الهامة‬ ‫الخصائﺺ‬ ‫بعض‬ ‫الخطي‬ ‫االرتباط‬ ‫ملعامل‬
. (‫)املوجب‬ ‫الطردي‬ ‫االرتباط‬ ‫حالة‬ ‫يف‬ ‫موجبة‬ r ‫تكون‬ -1
. (‫)السالب‬ ‫العكﴘ‬ ‫االرتباط‬ ‫حالة‬ ‫يف‬ ‫سالبة‬ r ‫تكون‬ -2
. ‫االرتباط‬ ‫انعدام‬ ‫حالة‬ ‫يف‬ ً‫ا‬‫ر‬‫صف‬ ‫تساوي‬ r ‫قيمة‬ -3
. ‫التام‬ ‫الطردي‬ ‫الرتباط‬ ‫حالة‬ ‫+يف‬1 ‫تساوي‬ r ‫قيمة‬ -4
. ‫التام‬ ‫العكﴘ‬ ‫االرتباط‬ ‫حالة‬ ‫يف‬ -1 ‫تساوي‬ r ‫قيمة‬ -5
‫قيمة‬ ‫اقرتبﺖ‬ ‫وكلﺎﻤ‬ [ -1 , +1 ] ‫بﻦﻴ‬ ‫تنحﴫ‬ ‫االرتباط‬ ‫معامل‬ ‫قيمة‬ ‫أن‬ ‫سبق‬ ‫مﺎﻤ‬ ‫ويالحﻆ‬
‫اقرتبﺖ‬ ‫وكلﺎﻤ‬ ‫الظاهرتﻦﻴ‬ ‫بﻦﻴ‬ ‫االرتباط‬ ‫قوة‬ ‫عىل‬ ً‫ال‬‫دلي‬ ‫هذا‬ ‫كان‬ -1‫أو‬+1 ‫من‬ ‫االرتباط‬ ‫معامل‬
. ‫االرتباط‬ ‫انعدام‬ ‫عىل‬ ً‫ال‬‫دلي‬ ‫هذا‬ ‫كان‬ ‫الصفر‬ ‫من‬ ‫قيمته‬
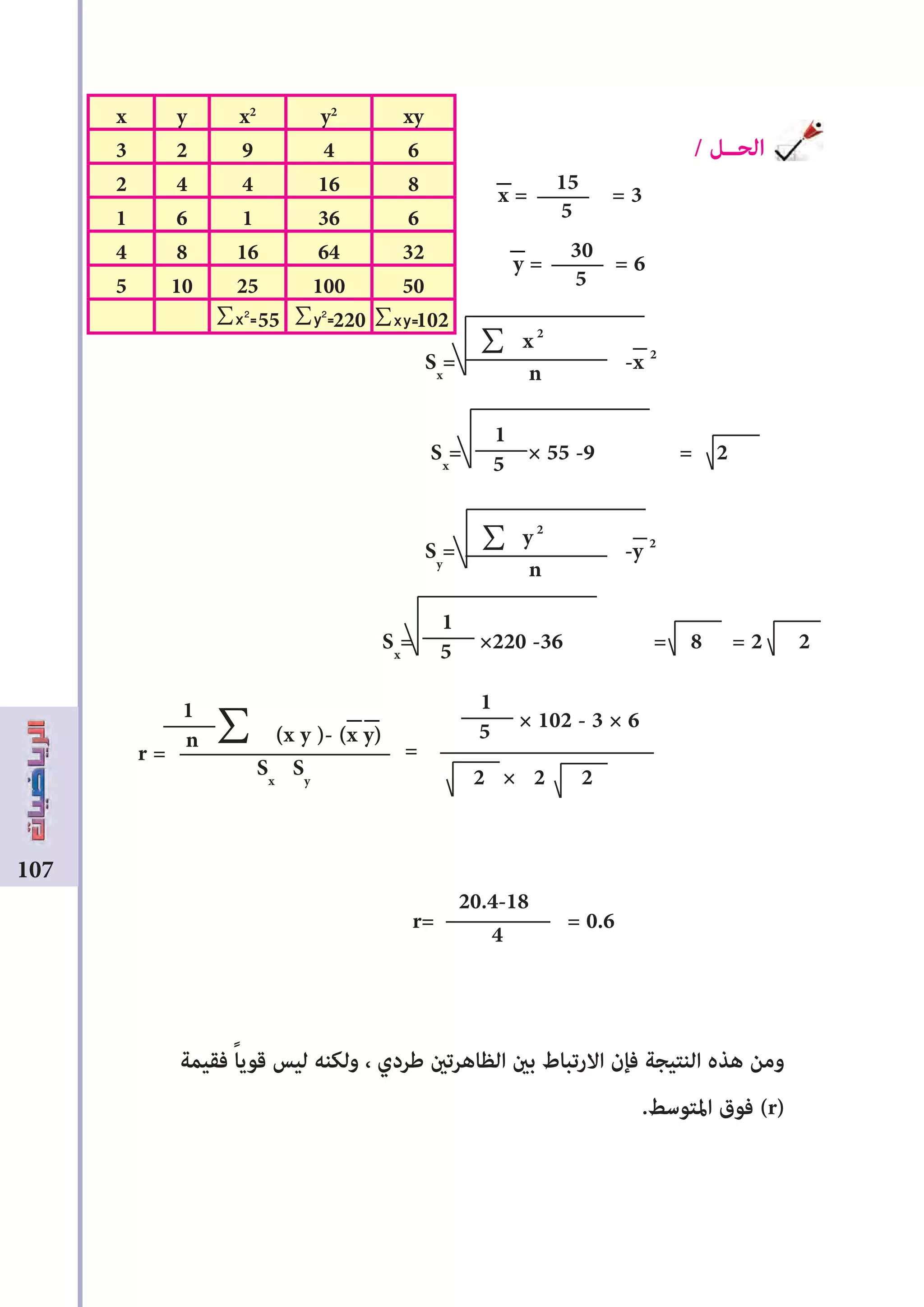
. ‫ﻇاهرتﻦﻴ‬ ‫قيم‬ ‫متثل‬ ‫التاﱄ‬ ‫الجدول‬ ‫يف‬ ‫املوضحة‬ x , y ‫أن‬ ‫افرض‬
. ‫بينهﺎﻤ‬ ‫االرتباط‬ ‫معرفة‬ ‫املطلوب‬
22‫مثال‬
54123x
108642y
∑
∑

107. 107
r =
/ ‫الحــل‬
x = = 3
y = = 6
Sx
= -x 2
Sx
= × 55 -9 = 2
Sy
= -y 2
Sx
= ×220 -36 = 8 = 2 2
(x y )- (x y)
r= = 0.6
‫فقيمة‬ ً‫ا‬‫قوي‬ ‫ليس‬ ‫ولكنه‬ ، ‫ﻃردي‬ ‫الظاهرتﻦﻴ‬ ‫بﻦﻴ‬ ‫االرتباط‬ ‫فﺈن‬ ‫النتيجة‬ ‫هذه‬ ‫ومن‬
.‫املتوسﻂ‬ ‫فوق‬ (r)
1
n =
Sx
Sy
∑
15
5
30
5
1
5
× 102 - 3 × 6
2 × 2 2
1
5
x2
n
y2
n
1
5
20.4-18
4
xyy2
x2
yx
64923
816442
636161
32641684
5010025105
10222055∑x2
= ∑y2
= ∑xy=
∑
∑

108. 108
: ‫اﻵﻲﺗ‬ ‫الجدول‬ ‫من‬ x , y ‫املتﻐري‬ ‫بﻦﻴ‬ ‫االرتباط‬ ‫معامل‬ ‫جد‬
. ‫املتﻐريين‬ ‫من‬ ‫لكل‬ ‫الحسايب‬ ‫الوسﻂ‬ ‫نحسب‬ / ‫الحــل‬
x = = 4
y = = 8
Sx
= = = 2
Sy
= = 8 = 2 2
65432x
1210864y
22‫مثال‬
20
5
40
5
( x - x )2
n
( y - y )2
n
40
5
10
5
(x- x)(y - y)(y- y)2
(x -x)2
y - yx - xyx
8164-4-242
241-2-163
0000084
24121105
816442126
204010//4020∑x= ∑y= ∑(x-x)2
= ∑(y-y)2
= ∑(x-x)(y-y)=
∑
∑

109. 109
r = = = 1
r = =
‫تام‬ ‫ﻃردي‬ ‫اإلرتباط‬ ∴
: ‫املثال‬ ‫لحل‬ ‫أخرى‬ ‫ﻃريقة‬
Sx
= _ (x)2
Sx
= × 90 - 16 = 2
Sy
= _ (y)2
= × 360 - 64 = 8 = 2 2
r= = =1
‫تام‬ ‫ﻃردي‬ ‫االرتباط‬ ∴
1
n (x y) - (x y )
Sx
Sy
∑
1
5
× 20
2 × 2 2
4
4
1
5
× 180 - 4 × 8
2 × 2 2
1
5 4
4
x2
n
y2
n
1
5
∑
∑

110. 110
: ‫التالية‬ ‫البيانات‬ ‫من‬ x ، y ‫الظاهرتﻦﻴ‬ ‫قيم‬ ‫بﻦﻴ‬ ‫االرتباط‬ ‫معامل‬ ‫جد‬ -1
‫نحصل‬ 4 ‫يف‬ x ‫الظاهرة‬ ‫قيم‬ ‫ﴐبﺖ‬ ‫لو‬ ‫األول‬ ‫السؤال‬ ‫يف‬ ‫املبﻦﻴ‬ ‫الجدول‬ ‫يف‬ -2
: ‫وهو‬ ‫آخر‬ ‫جدول‬ ‫عىل‬
. ‫األول‬ ‫السؤال‬ ‫نتيجة‬ ‫مع‬ ‫النتيجة‬ ‫وقارن‬ ‫اإلرتباط‬ ‫معامل‬ ‫جد‬
: ‫التاﱄ‬ ‫الجدول‬ ‫يف‬ ‫االرتباط‬ ‫معامل‬ ‫جد‬ -3
r =+ 1 ‫اﳉﻮاب‬
‫ﺗﺎم‬ ‫ﻃﺮدي‬ ‫اﻻرﺗﺒﺎط‬
321x
642y
1284x
642y
108642x
54321y
(5-3) ‫متارين‬

111. 111
4 ............ ‫الحقيقية‬ ‫الدوال‬ : ‫االول‬ ‫الفصل‬
23 ....... ‫اجحات‬‫رت‬‫وامل‬ ‫املعادالت‬ : ‫الثاين‬ ‫الفصل‬
43 ............... ‫املثلثات‬ ‫حساب‬ : ‫الثالث‬ ‫الفصل‬
63 ............ ‫االحداثية‬ ‫الهندسة‬ : ‫ابع‬‫ر‬‫ال‬ ‫الفصل‬
77 ....................... ‫االحصاء‬ : ‫الخامس‬ ‫الفصل‬
‫اﶈﺘﻮﻳﺎت‬

112. 112
‫ﰎ‬
‫ﷲ‬‫ا‬ ‫ﺪ‬‫ﻤ‬‫ﺤ‬‫ﺑ‬