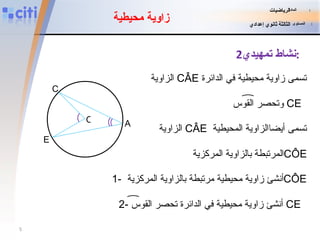
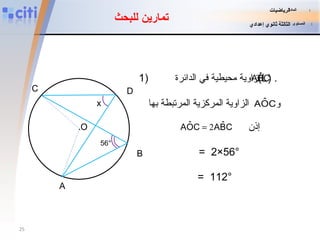
يتناول المستند موضوع الزوايا المركزية والزوايا المحيطية في الرياضيات، حيث يشرح كيف يتم تحديد هذه الزوايا وعلاقتها ببعضها البعض. يحتوي على أنشطة تمهيدية توضح خصائص هذه الزوايا وأهميتها في الدوائر، مع توضيح كيفية حساب الزوايا المرتبطة. كما يتضمن تمارين للبحث تساعد في تطبيق المفاهيم المكتسبة.

1. الزوايا المركزية و الزوايا المحيطية المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي

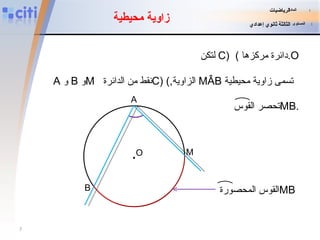
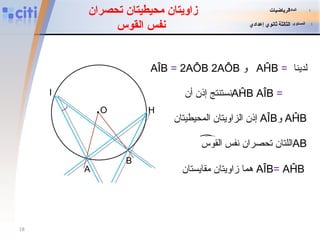
2. زاوية مركزية نشاط تمهيدي 1 : في هذا الشكل الزاوية BÔA رأسها هومركز الدائرة (C) و [OA] و OB] ] شعاعان للدائرة .(C) الزاوية BÔA تسمى الزاوية المركزية حدد زوايا مركزية أخرى في هذا الشكل . المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي o C A D B O التي تحصر القوس AB

3. زاوية مركزية الزاوية BÔD زاوية مركزية الزاوية DÔC زاوية مركزية الزاوية BÔC زاوية مركزية الزاوية AÔB زاوية مركزية الزاوية AÔC زاوية مركزية المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي o C A D B O

4. زاوية مركزية لتكن (C) دائرة مركزها O و A و B نقطتان من هذه الدائرة المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي AÔB تسمى الزاوية المركزية التي تحصر القوس AB o A B O

5. زاوية محيطية نشاط تمهيدي 2 : الزاوية CÂE تسمى زاوية محيطية في الدائرة الزاوية CÂE تسمى أيضاالزاوية المحيطية المرتبطة بالزاوية المركزية CÔE 1 - أنشئ زاوية محيطية مرتبطة بالزاوية المركزية CÔE المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي o A E C O وتحصر القوس CE 2- أنشئ زاوية محيطية في الدائرة تحصر القوس CE

6. الزاوية المحيطية التي تحصر الزاوية المحيطية المرتبطة بالزاوية زاوية محيطية o A E C O المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي M P ^ المركزية CÔE هي CPE . ^ القوس CE هي C M E .

7. لتكن C) ( دائرة مركزها .O A و B و M نقط من الد ا ئرة C) ( , الزاوية MÂB تسمى زاوية محيطية زاوية محيطية M B A . O تحصر القوس MB . القوس المحصورة MB المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي

8. زاوية محيطية المماس للدائرة C) ( في النقطة A A B . O T المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي الزاوية المحيطية TÂB تحصر القوس AB

9. (1 حدد علاقة بين a و b و .c (2 أحسب AÔI بدلالة a . .AÔI = 2AĤI استنتج أن (3 زاوية محيطية والزاوية المركزية المرتبطة بها نشاط تمهيدي 3 : في هذا الشكل نضع OÂI = a و b = AĤO و OÎH = c المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي a O . A I H b c

10. OAI(1 مثلث متساوي الساقين في النقطة O يعني أن AÎO = a OÂI = OAH مثلث متساوي الساقين في النقطة O يعني أن AĤO = b OÂH = OIH مثلث متساوي الساقين في النقطة O يعني أن OÎH = OĤI = c إذن : a + b + b + c + c + a = 180° 2a + 2b + 2c = 180° 2(a + b + c) = 180° a + b + c = 90° زاوية محيطية والزاوية المركزية المرتبطة بها المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي a O . A I H b c

11. (2 نعلم أن مجموع قياسات زوايا مثلث هو 180° إذن (3 لدينا : AÔI = 180° - 2a = 2(a + b + c) - 2a = 2a + 2b + 2c - 2a = 2(b + c) = 2AĤI AÔI = 180° - 2a زاوية محيطية والزاوية المركزية المرتبطة بها المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي a O . A I H b c

12. زاوية محيطية والزاوية المركزية المرتبطة بها نشاط تمهيدي 4 : في هذا الشكل (AT) مماس للدائرة (c) و AÔB x= و a = OÂB و t =TÂB -1 أحسب x بدلالة a 2 - بين أن 2TÂB AÔB = أي x = 2t x O a A B T المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي

13. زاوية محيطية والزاوية المركزية المرتبطة بها 1- OAB مثلث متساوي الساقين في O يعني أن زا و يتي قاعدته متقايستان إذن x + a + a = 180° يعني أن x + 2a = 180° يعني أن x = 180° - 2a x O a A B T المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي

14. زاوية محيطية والزاوية المركزية المرتبطة بها 2- x = 180° - 2a x O a A B T = t + a + 90° - 2a = t + 90° - a = t + t 2TÂB AÔB = إذن المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي

15. زاوية محيطية والزاوية المركزية المرتبطة بها خاصية 1 قياس زاوية مركزية BÔM يساوي ضعف قياس أية زاوية محيطية نكتب 2 BÂM BÔM = A M B O المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي BÂM تحصر نفس القوس BM

16. زاوية محيطية والزاوية المركزية المرتبطة بها خاصية 2 ليكن (∆) المماس للدائرة ( C ) عند النقطة A نكتب 2 BÂM BÔM = BÂM و T نقطة من (∆) لدينا : TÂB AÔB = 2 المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي O B T A

17. زاويتان محيطيتان تحصران نفس القوس نشاط تمهيدي 5 : نعتبر الشكل التالي : بين أن AÎB = AĤB واستنتج الخاصية المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي I H B A . O

18. زاويتان محيطيتان تحصران نفس القوس I H B A . O لدينا AÎB = 2AÔB و 2AÔB AĤB = نستنتج إذن أن AĤB AÎB = إذن الزاويتان المحيطيتان AÎB و AĤB هما زاويتان مقايستان AÎB = AĤB اللتان تحصران نفس القوس AB المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي

19. فإنهما تكونان متقايست ي ن . زاويتان محيطيتان تحصران نفس القوس خاصية 3 إذا حصرت زاويتان محيطيتان في دائرة نفس القوس المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي

20. حالة خاصة : زاويتان محيطيتان تحصران نفس القوس خاصية 4 A و T نقطة من (∆) لدينا AÎB = TÂB ليكن (∆) المماس للدائرة ( C ) عند النقطة المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي O B T A I (∆)

21. لتكن ( C ) دائرة مركزها O D و T و C و F نقط من ( C ) كما هو مبين في الشكل . 2 ) حدد قياس الزاوية DÔC . تمرين 1 تمارين للبحث D . O F T C 25° 48° 1) حدد قياس الزاوية و قياس الزاوية المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي

22. إذن فهما متقايستان . يعني أن إذن فهما متقايستان . يعني أن تمارين للبحث D . O F T C 25° 48° 1- لدينا و زاويتان محيطيتان - لدينا و زاويتان محيطيتان المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي في نفس الدائرة تحصران نفس القوس FT في نفس الدائرة تحصران نفس القوس FT

23. تمارين للبحث D . O F T C 25° 48° إذن = 2×48° = 96° المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي 2- زاوية محيطية مرتبطة بالزاوية المركزية

24. تمارين للبحث ( L ) دائرة مركزها O A و B و C نقط من ( L ) حيث (BC) يقطع (AD) في E 1 ) أحسب AÔC 2) أحسب .x تمرين 2 المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي . O A B D 56° x C

25. . O A B D 56° x C تمارين للبحث إذن = 2×56° = 112° المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي 1) زاوية محيطية في الدائرة ( L ) . و الزاوية المركزية المرتبطة بها

26. . O A B D 56° x C تمارين للبحث إذن المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي و زاويتان محيطيتان في الدائرة (L) تحصران نفس القوس AC

27. لنعتبر دائرة (C) مركزها B و (C') دائرة مركزها .B' مختلفتان و ت تقاطعان في نقطة K كما هو مبين في الشكل تمرين 3 تمارين للبحث ^ بين أن = A'B'C' ABC ^ . B B' . K A' C' A C المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي

28. . B B' . K A' C' A C و وبما أن فإن أي أن ( زاويتان متقابلتان با لرأس ) لدينا تمارين للبحث المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي

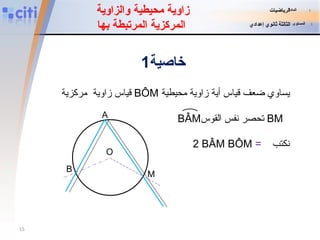
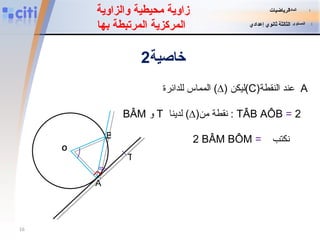
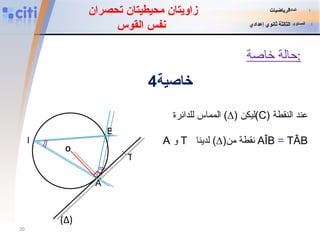
29. ABC مثلث محاط بدائرة (C) مركزها O وشعاعها [OM] عمودي على الضلع .[BC] تمرين 4 تمارين للبحث . O A B C M أثبت أن نصف المستقيم [AM) منصف الزاوية المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي

30. OBC مثلث متساوي الساقين في O الإرتفاع [OM] هو كذلك منصف ال زاوية B ÔC إذن الزاوية المحيطية B Â M والزاوية المركزية B Ô M الزاوية المحيطية M Â C والزاوية المركزية M Ô C وبما أن فإن أي أن [AM) منصف الزاوية B Â C إذن إذن . O A B C M تمارين للبحث تحصران نفس القوس .BM المادة : الرياضيات المستوى : الثالثة ثانوي إعدادي تحصران نفس القوس MC .