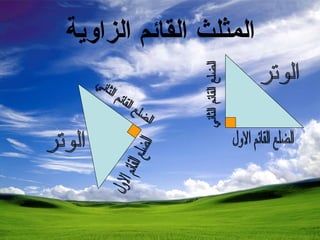
تناقش نظرية فيثاغورس العلاقة بين أطوال أضلاع المثلث القائم الزاوية، حيث تُستخدم المعادلة ع^2 = س^2 + ص^2. تتضمن الدروس تحديد نص النظرية، إثبات صحتها، وحل تمارين تتعلق بالمثلثات القائمة الزاوية. تشمل الأمثلة التطبيقية حساب طول الوتر أو أحد الأضلاع باستخدام المعادلة المذكورة.

1. ‫نظرية فيثاغورس‬

2. ‫أهداف الدرس‬
‫• أن تتعرف على نظرية فيثاغورس.‬
‫• أن تذكر نص نظرية فيثاغورس.‬
‫• أن تثبت صحة نظرية فيثاغورس.‬
‫• ان تحل تمارين على المثلث القائم الزاوية‬
‫باستخدام نظرية فيثاغورس.‬
‫• أن يوظف نظرية فيثاغورس في حل مسائل‬
‫حياتية‬

3. ‫المثلث القائم الزاوية‬

4. ‫‪‬نرسم مثلث قائم الزاوية أطوال اضلعه س،ص،ع‬
‫‪‬نرسم على كل ضلع مربع‬
‫‪‬نحسب مساحة كل مربع حسب القانون‬
‫2‬
‫مساحة المربع = )طول الضلع(‬
‫ع۲‬
‫ع‬
‫س‬ ‫س‬
‫ص‬
‫2‬
‫ص۲‬

5. ‫‪‬نضع‬
‫المربعات‬
‫الصغيرة على‬
‫المربع‬
‫المرسوم على‬
‫الوتر لتغطيته‬
‫كامل‬

6. ‫‪‬نستنتج ان مساحة المربع المنشأ على وتر المثلث‬
‫القائم الزاوية تساوي مجموع مساحتي المربعين‬
‫المنشأين على ضلعي القائمة‬
‫2‬
‫‪‬أو بالرموز ع2 = س2 + ص‬
‫ع‬
‫س‬
‫ص‬

7. ‫مثال1:‬
‫س ص ع مثلث قائم الزاوية في ص طول س ص‬
‫س‬
‫= 6 سم ، ص ع = 8 سم احسب طول س ع‬
‫‪‬نستخدم نظرية فيثاغورس‬
‫س6‬ ‫2‬
‫ع2 = س2 + ص‬
‫ع‬ ‫ص‬
‫س8‬ ‫م‬
‫2‬
‫ع2 = )6(2 + )8(‬
‫م‬
‫ع2 = 63 + 46‬
‫ع = 01‬ ‫ع = 001‬ ‫ع2 = 001‬

8. ‫مثال أ ب ج مثلث قائم الزاوية في ب طول‬
‫2:‬
‫أب = 5 سم‬
‫أ‬
‫‪‬نستخدم نظرية فيثاغورس‬
‫ع2 = أج = 31 سم احسب طولس31 ج؟‬
‫ب‬ ‫2‬
‫س2 + ص‬
‫س5‬
‫ج‬ ‫م‬
‫2‬
‫)31(2 = )5(2 + ص‬
‫ب‬
‫م‬ ‫961 = 52 + ص‬
‫2‬
‫2‬
‫961 - 52= ص‬
‫ص = 21سم‬ ‫ص = 441‬ ‫2‬
‫441= ص‬
‫ب ج = 21سم‬

9. ‫واجب أ ب ج مثلث قائم الزاوية في ب طول‬
‫أب = 21 سم‬
‫أ‬
‫أج = 02 سم احسبي طول ب ج؟‬
‫س02‬
‫س21‬
‫ج‬ ‫م‬ ‫ب‬
‫م‬

10. ‫تمارين الكتاب‬

11. ‫مثال1:‬
‫أ ب جـ مثلث فيه أ ب = 9سم، ب جـ= 21سم ،أ جـ= 51سم‬
‫هل المثلث قائم الزاوية ؟‬
‫2‬
‫الحـل : )أب(2 = 9 = 18‬
‫‪‬‬
‫2‬
‫)ب جـ(2 = 21 = 441‬
‫2‬
‫)أجـ(2 =51 = 522‬
‫أ‬
‫‪h‬‬ ‫ب‬
‫ب‬ ‫أ‬
‫‪ ‬أب ‪ Ì‬أ‬
‫أيأـــن‬
‫اذ ا ًا ــلمثلثق ــائم‬
‫ـ‬ ‫ـ‬
‫وتسمىاـــلعدادأـــعدادا‬
‫الزاوية‬

12. ‫مثال2:‬
‫أ ب جـ مثلث فيه أ ب = 5سم، ب جـ= 7سم ،أ جـ= 8سم‬
‫هل المثلث قائم الزاوية ؟‬
‫2‬
‫الحـل : )أب(2 = 5 = 52‬
‫‪‬‬
‫2‬
‫)ب جـ(2 = 7 = 94‬
‫2‬
‫)أجـ(2 =8 = 46‬
‫أ‬
‫أ‬ ‫ب‬
‫ب‬ ‫أ‬
‫‪  ‬أ‬
‫‪ ‬أب‬
‫م‬
‫اذاًاـــلمثلثغـــيرقـــائ‬