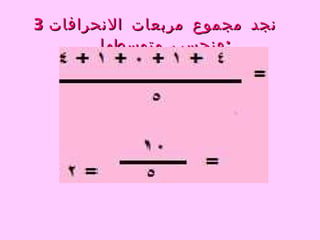
الانحراف المعياري هو الجذر التربيعي لمتوسط مجموع مربعات الانحرافات عن الوسط الحسابي، ويشمل خطوات حسابه لمجموعة بيانات محددة مثل حساب الأعداد من 1 إلى 5 أو بيانات تكرارية لعائلات فلسطينية. يتضمن الحل حساب الوسط الحسابي والانحرافات ومربعاتها وإيجاد المتوسطات المطلوبة للحصول على الانحراف المعياري النهائي.

1. الانحراف المعياري يعرف الانحراف المعياري بأنه الجذر التربيعي لمتوسط مجموع مربعات انحرافات القيم عن وسطها الحسابي فإذا كانت مفردات عددها ن ووسطها الحسابي

2. الانحراف المعياري بالرموز أو حيث الوسط الحسابي لمجموعة البيانات التي عددها ن

3. احسب الانحراف المعياري لمجموعة البيانات التالية : 1 ,2 ,3 , 4 , 5 الـــحــــل : 1. نحسب الوسط الحسابي

4. 2. نحسب الانحرافات عن الوسط الحسابي ونربعها س 1 3 -2 4 2 3 -1 1 3 3 صفر صفر 4 3 1 1 5 3 2 4 المجموع 10

5. 3. نجد مجموع مربعات الانحرافات ونحسب متوسطها :

6. 4. نجد الجذر التربيعي لمتوسط مربعات الانحرافات عن وسطها الحسابي فيكون الانحراف المعياري يساوي أو بالرموز

7. أما في حالة حساب الانحراف المعياري للجداول التكرارية فإننا نستعمل الصيغه الآتية حيث :- س : تمثل القيمة او مركز الفئة : الوسط الحسابي ت : تكرار الفئة ن : مجموع التكرار

8. احسب الانحراف المعياري لعدد الأطفال : مثال (2): الجدول التكراري الآتي يمثل عدد الأطفال لخمسين عائلة فلسطينية : عدد الأطفال صفر 1 2 3 4 5 6 عدد العائلات 5 5 9 10 12 5 4

9. الحـل :- عدد الاطفال ( س ) عدد العائلات ( ت ) ت * س س - س ( س - س ) 2 ت *( س - س )2 صفر 5 صفر -3 9 45 1 5 5 -2 4 20 2 9 18 -1 1 9 3 10 30 صفر صفر صفر 4 12 48 1 1 12 5 5 25 2 4 20 6 4 24 3 9 36 المجموع 50 150 142

10. 1. نحسب الوسط الحسابي لعدد الأطفال : = = 2. نحسب الانحرافات عن الوسط الحسابي 3. نربع الانحرافات عن الوسط الحسابي 4. نضرب مربع الانحرافات عن الوسط الحسابي في التكرار ونجد مجموع هذا العمود الذي يساوي 142

11. 5. نطبق صيغة الانحراف المعياري :