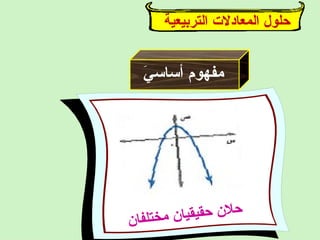
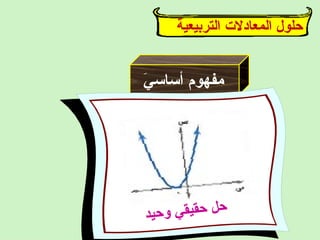
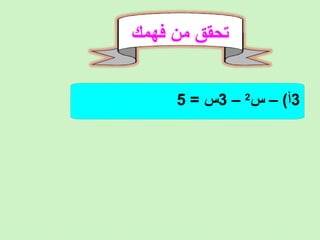
تتناول الوثيقة كيفية حل المعادلات التربيعية وتمثيلها بيانياً، مع توضيح استخدامات الجذور والمقاطع السينية في تحليل الدوال. تقدم الوثيقة خطوات لحل المعادلات التربيعية وتحقق صحة الحلول باستخدام التحليل الرياضي. كما تتضمن أمثلة توضح طرق الكتابة القياسية للمعادلات وتأثيرها على حلها.

1. 8-2‫ا‬ً‫بياني‬ ‫التربيعية‬ ‫المعادل ت‬ ‫حل‬ :

2. ‫ق‬‫ب‬‫س‬ ‫ا‬‫م‬‫ي‬‫ف‬
‫ى‬‫ل‬‫إ‬ ‫ل‬‫ي‬‫ل‬‫ح‬‫ت‬‫ل‬‫ا‬‫ب‬ ‫ة‬‫ي‬‫ع‬‫ي‬‫ب‬‫ر‬‫ت‬‫ل‬‫ا‬ ‫ ت‬‫ل‬‫د‬‫ا‬‫ع‬‫م‬‫ل‬‫ا‬ ‫ل‬‫ح‬ ‫ت‬‫س‬‫ر‬‫د‬
.‫ل‬‫م‬‫ا‬‫و‬‫ع‬‫ل‬‫ا‬

3. ‫والن‬
•‫ا‬ً‫بياني‬ ‫التربيعية‬ ‫المعادل ت‬ ‫أحل‬.
•‫التربيعية‬ ‫المعادل ت‬ ‫حلول‬ ‫أقدر‬
‫البياني‬ ‫تمثيلها‬ ‫من‬.

4. ‫ ت‬‫ا‬‫د‬‫ر‬‫ف‬‫م‬‫ل‬‫ا‬
‫المكرر‬ ‫الجذر‬

5. ‫لماذا؟‬
‫قدم‬ ‫لكرة‬ ‫المنحنى‬ ‫المسار‬ ‫عن‬ ‫يعبر‬
= ‫ص‬ ‫بالدالة‬ ‫ملعب‬ ‫داخل‬ ‫رلكلت‬ُ
-0.005‫س‬2
+ ‫س‬ +5‫حيث‬ ‫؛‬
‫قطعتها‬ ‫التي‬ ‫الفقية‬ ‫المسافة‬ (‫)س‬
‫الكرة‬ ‫ارتفاع‬ (‫)ص‬ ،‫بالقدام‬ ‫الكرة‬
‫بالقدام‬ ‫الرض‬ ‫سطح‬ ‫فوق‬.

6. ‫لماذا؟‬
‫السينية‬ ‫المقاطع‬ ‫استعمال‬ ‫ويمكن‬
‫لتحديد‬ ‫الدالة‬ ‫لهذه‬ ‫البياني‬ ‫للتمثيل‬
‫ستقطعها‬ ‫التي‬ ‫الفقية‬ ‫المسافة‬
‫الرض‬ ‫تلمس‬ ‫حتى‬ ‫الكرة‬.

7. ‫الصورة‬ :‫البياني‬ ‫بالتمثيل‬ ‫التربيعية‬ ‫المعادلة‬ ‫حل‬
‫القياسية‬:‫هي‬ ‫التربيعية‬ ‫للمعادلة‬
‫أس‬2
= ‫ج‬ + ‫س‬ ‫ب‬ +0‫يساوي‬ ‫ل‬ ‫أ‬ ‫حيث‬ ،0‫ولكتابة‬ ،
‫د‬ ‫أو‬ ‫ص‬ ‫استبدل‬ ،‫معادلة‬ ‫صورة‬ ‫على‬ ‫التربيعية‬ ‫الدالة‬
‫يمكن‬ ‫جذورها‬ ‫أو‬ ‫المعادلة‬ ‫حلول‬ ‫أن‬ ‫وتذلكر‬ ،‫بصفر‬ (‫)س‬
‫للدالة‬ ‫البياني‬ ‫للتمثيل‬ ‫السينية‬ ‫المقاطع‬ ‫بإيجاد‬ ‫تحديدها‬
‫أو‬ ‫حقيقيان‬ ‫حلن‬ ‫التربيعية‬ ‫للمعادلة‬ ‫ويوجد‬ ،‫المرتبطة‬
.‫حقيقية‬ ‫حلول‬ ‫لها‬ ‫يوجد‬ ‫ل‬ ‫أو‬ ،‫واحد‬ ‫حقيقي‬ ‫حل‬

8. ‫ي‬َ ‫أساس‬ ‫مفهوم‬
‫التربيعية‬ ‫المعادل ت‬ ‫حلول‬
‫ن‬‫ا‬‫ف‬‫ل‬‫ت‬‫خ‬‫م‬ ‫ن‬‫ا‬‫ي‬‫ق‬‫ي‬‫ق‬‫ح‬ ‫ن‬‫ل‬‫ح‬

9. ‫ي‬َ ‫أساس‬ ‫مفهوم‬
‫التربيعية‬ ‫المعادل ت‬ ‫حلول‬
‫د‬‫ي‬‫ح‬‫و‬ ‫ي‬‫ق‬‫ي‬‫ق‬‫ح‬ ‫ل‬‫ح‬

10. ‫ي‬َ ‫أساس‬ ‫مفهوم‬
‫التربيعية‬ ‫المعادل ت‬ ‫حلول‬
‫ة‬‫ي‬‫ق‬‫ي‬‫ق‬‫ح‬ ‫ل‬‫و‬‫ل‬‫ح‬ ‫د‬‫ج‬‫و‬‫ي‬ ‫ل‬

11. ‫ل‬‫ا‬‫ث‬‫م‬1
‫ن‬‫ا‬‫ف‬‫ل‬‫ت‬‫خ‬‫م‬ ‫ن‬‫ا‬‫ي‬‫ق‬‫ي‬‫ق‬‫ح‬ ‫ن‬‫ا‬‫ر‬‫ذ‬‫ج‬
‫س‬ ‫المعادلة‬ ‫حل‬2
–2– ‫س‬8=0‫ا‬ً‫بياني‬.
‫س‬ = (‫)س‬ ‫د‬ ‫الدالة‬ ‫مثل‬2
–2– ‫س‬8
.‫ا‬ً‫بياني‬ ‫بالمعادلة‬ ‫المرتبطة‬
‫البياني‬ ‫للتمثيل‬ ‫السينية‬ ‫المقاطع‬ ‫تظهر‬
- ‫عند‬2،4- ‫هي‬ ‫فالحلول‬ ‫لذا‬ .2،4.

12. :‫تحقق‬‫الصلية‬ ‫المعادلة‬ ‫في‬ ‫بالتعويض‬ ‫حل‬ ‫لكل‬ ‫صحة‬ ‫من‬ ‫تحقق‬.
‫س‬2
–2‫س‬–8=0‫الصلية‬ ‫المعادلة‬‫س‬2
–2‫س‬–8=
0-)2(2
–2-)2(–8=0- = ‫س‬2= ‫أوس‬4
)4(2
–2)4(–8=0
0=0√‫بسط‬0=0√

13. ‫الدرس‬ ‫موضوع‬‫التربيعية‬ ‫المعادلت‬ ‫حل‬‫ب‬‫يانيا‬
‫س‬: ‫بيانيا‬ ‫التالية‬ ‫المعادلة‬ ‫حلي‬
1(‫س‬2‫ـ‬4+ ‫س‬3=0
000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000
2(‫س‬2- =8– ‫س‬16
‫ابراهيم‬ ‫نجلء‬ ‫م‬
‫عمـــــــــــــل‬ ‫ورقة‬

14. ‫فهمك‬ ‫من‬ ‫تحقق‬
1‫س‬ (‫ب‬2
–4+ ‫س‬3=0

15. ‫الحـــــــــــــــــــل‬
•= ‫س‬ ‫التماثل‬ ‫محور‬2
•) ‫الرأس‬2‫ــ‬ ،1(
•= ‫جـ‬ = ‫الصادي‬ ‫المقطع‬3

16. ‫البياني‬ ‫التمثيل‬

17. ‫الحـــــــــــــــــــــــــــــــــــــــــل‬
= ‫ح‬{1،3}
: ‫التحقق‬
‫س‬2‫ــ‬4+ ‫س‬3=0
‫أو‬ ‫اما‬
)1(‫ــ‬4)1+(3=0)3‫ــ‬ (4)3+ (3=0
2 2

18. ‫ل‬‫ا‬‫ث‬‫م‬ ‫ي‬‫ف‬ ‫ة‬‫ل‬‫د‬‫ا‬‫ع‬‫م‬‫ل‬‫ا‬ ‫ل‬‫و‬‫ل‬‫ح‬
1
‫ن‬‫ا‬‫ي‬‫ق‬‫ي‬‫ق‬‫ح‬ ‫ن‬‫ا‬‫د‬‫د‬‫ع‬
‫ا‬‫م‬‫ه‬ ‫ن‬‫ا‬‫ر‬‫ذ‬‫ج‬‫ل‬‫ا‬ ‫ن‬‫و‬‫ك‬‫ي‬ ‫ا‬ً‫ن‬‫ا‬‫ي‬‫ح‬‫أ‬ ‫ه‬‫ن‬‫أ‬ ‫ل‬‫إ‬ ،‫ن‬‫ا‬‫ف‬‫ل‬‫ت‬‫خ‬‫م‬
‫ا‬‫ه‬‫د‬‫ن‬‫ع‬ ‫ى‬‫م‬‫س‬‫ي‬ُ‫و‬ ،‫ه‬‫س‬‫ف‬‫ن‬ ‫د‬‫د‬‫ع‬‫ل‬‫ا‬
‫ا‬ً‫ر‬‫ر‬‫ك‬‫م‬ ‫ا‬ً‫ر‬‫ذ‬‫ج‬
.

19. :‫ه‬‫ي‬‫ب‬‫ن‬‫ت‬

20. ‫ل‬‫ا‬‫ث‬‫م‬2
:‫ر‬‫ر‬‫ك‬‫م‬ ‫ر‬‫ذ‬‫ج‬
‫س‬ :‫المعادلة‬ ‫حل‬2
-6- = ‫س‬9‫يا‬ًّ‫بيان‬
‫الخطوة‬1:‫بالصورة‬ ‫المعادلة‬ ‫كتابة‬ ‫أعد‬
.‫القياسية‬
‫س‬2
-6- = ‫س‬9‫اللصلية‬ ‫المعادلة‬
‫س‬2
-6+ ‫س‬9=0‫أضف‬9‫الطرفين‬ ‫كل‬ ‫إلى‬

21. ‫س‬ :‫المعادلة‬ ‫حل‬2
-6- = ‫س‬9‫يا‬ًّ‫بيان‬
‫الخطوة‬2:‫س‬ = (‫)س‬ ‫د‬ ‫المرتبطة‬ ‫الدالة‬ ‫ثل‬ّ‫ل‬‫م‬2
–6+ ‫س‬9
‫الخطوة‬3:‫رأس‬ ‫أن‬ ‫ولحظ‬ ،‫البياني‬ ‫للتمثيل‬ ‫السيني‬ ‫المقطع‬ ‫حدد‬
‫للمعادلة‬ ‫فإن‬ ‫لذا‬ ،‫للدالة‬ ‫الوحيد‬ ‫السيني‬ ‫المقطع‬ ‫هو‬ ‫المكافئ‬ ‫القطع‬
‫هو‬ ‫ا‬ً‫وحيد‬ ‫ل‬ً ‫ح‬3.

24. ‫فهمك‬ ‫من‬ ‫تحقق‬
2‫س‬ (‫أ‬2
+25=10‫س‬
5

25. ‫ن‬‫و‬‫ك‬‫ت‬ ‫ة‬‫ي‬‫ع‬‫ي‬‫ب‬‫ر‬‫ت‬‫ل‬‫ا‬ ‫ة‬‫ل‬‫د‬‫ا‬‫ع‬‫م‬‫ل‬‫ا‬ ‫ر‬‫و‬‫ذ‬‫ج‬ ‫ن‬‫أ‬ ‫ا‬‫م‬‫ك‬
.‫ة‬‫ي‬‫ق‬‫ي‬‫ق‬‫ح‬ ‫ر‬‫ي‬‫غ‬ ‫ا‬ً‫د‬‫ا‬‫د‬‫ع‬‫أ‬ ‫ا‬ً‫ن‬‫ا‬‫ي‬‫ح‬‫أ‬

26. :‫ة‬‫ي‬‫ق‬‫ي‬‫ق‬‫ح‬ ‫ر‬‫و‬‫ذ‬‫ج‬ ‫د‬‫ج‬‫و‬‫ي‬ ‫ل‬
‫س‬ :‫المعادلة‬ ‫حل‬2
-6- = ‫س‬9‫يا‬ًّ‫بيان‬
‫الخطوة‬2:‫س‬ = (‫)س‬ ‫د‬ ‫المرتبطة‬ ‫الدالة‬ ‫ثل‬ّ‫ل‬‫م‬2
–6+ ‫س‬9
‫الخطوة‬3:‫رأس‬ ‫أن‬ ‫ولحظ‬ ،‫البياني‬ ‫للتمثيل‬ ‫السيني‬ ‫المقطع‬ ‫حدد‬
‫للمعادلة‬ ‫فإن‬ ‫لذا‬ ،‫للدالة‬ ‫الوحيد‬ ‫السيني‬ ‫المقطع‬ ‫هو‬ ‫المكافئ‬ ‫القطع‬
‫هو‬ ‫ا‬ً‫وحيد‬ ‫ال‬ً ‫ح‬3.
‫مثال‬3:
‫الخطوة‬1:‫القياسية‬ ‫بالصورة‬ ‫المعادلة‬ ‫كتابة‬ ‫أعد‬
‫القياسية‬ ‫بالصورة‬ ‫مكتوبة‬ ‫المعادلة‬

27. ‫للعدد‬ ‫عوامل‬ ‫يوجد‬ ‫ل‬10- ‫مجموعها‬3‫لذا‬ ،
‫أنه‬ ‫أي‬ ،‫العوامل‬ ‫إلى‬ ‫للتحليل‬ ‫قابلة‬ ‫غير‬ ‫فالعبارة‬
.‫حقيقية‬ ‫ل‬ً ‫حلو‬ ‫للمعادلة‬ ‫يوجد‬ ‫ل‬

28. ‫فهمك‬ ‫من‬ ‫تحقق‬
3– (‫أ‬‫س‬2
–3= ‫س‬5

29. ‫الحـــــــــــــــــــل‬
•‫ــ‬ = ‫س‬ ‫التماثل‬ ‫محور‬5,1
•‫)ــ‬ ‫الرأس‬5,1‫ــ‬ ,7،2(
•‫ــ‬ = ‫جـ‬ = ‫الصادي‬ ‫المقطع‬5

30. ‫البياني‬ ‫التمثيل‬

31. ‫الحـــــــــــــــــــــــــــــــــــــــــل‬
= ‫ح‬
: ‫التحقق‬‫الى‬ ‫بالتحليل‬ ‫المعادلة‬ ‫حل‬‫العدد‬ ‫عوامل‬8‫ومجموعهم‬6
‫للعدد‬ ‫عوامل‬ ‫يوجد‬ ‫ل‬8= ‫مجموعهما‬6‫يوجد‬ ‫ل‬ ‫انه‬ ‫أي‬
‫حقيقية‬ ‫حلول‬ ‫للمعادلة‬
Φ

32. ‫الحـــــــــــــــــــــــل‬
= ‫ح‬Φ

33. :‫للدراسة‬ ‫إرشادات‬:‫للدراسة‬ ‫إرشادات‬
:‫الفصفار‬ ‫مواقع‬
‫لذا‬ ،‫متصلة‬ ‫دوال‬ ‫التربيعية‬ ‫الدوال‬ ‫أن‬ ‫بما‬
‫اللتين‬ ‫س‬ ‫قيمتي‬ ‫بين‬ ‫فصفر‬ ‫يوجد‬ ‫أن‬ ‫يجب‬
‫من‬ ‫الشارة‬ ‫في‬ ‫متعاكستان‬ ‫قيمتان‬ ‫يقابلهما‬
.‫ص‬

34. :‫الحلول‬ ‫تقدير‬
‫ا‬ً‫أعداد‬ ‫السابقة‬ ‫للمعادلت‬ ‫وجدت‬ ‫التي‬ ‫الجذور‬ ‫ثل‬ّ‫ل‬‫تم‬
‫ا‬ً‫دائم‬ ‫ليست‬ ‫التربيعية‬ ‫المعادلت‬ ‫جذور‬ ‫أن‬ ‫إل‬ ،‫فصحيحة‬
‫قيم‬ ‫ليجاد‬ ‫التقدير‬ ‫الحالت‬ ‫هذه‬ ‫في‬ ‫ويستعمل‬ ،‫كذلك‬
.‫المعادلة‬ ‫لجذور‬ ‫تقريبية‬
‫ر‬‫ي‬‫د‬‫ق‬‫ت‬
:‫ل‬‫و‬‫ل‬‫ح‬‫ل‬‫ا‬‫ر‬‫ي‬‫د‬‫ق‬‫ت‬
:‫ل‬‫و‬‫ل‬‫ح‬‫ل‬‫ا‬

35. ‫ل‬‫ا‬‫ث‬‫م‬4
:‫ل‬‫و‬‫د‬‫ج‬‫ل‬‫ا‬ ‫ل‬‫ا‬‫م‬‫ع‬‫ت‬‫س‬‫ا‬‫ب‬ ‫ر‬‫و‬‫ذ‬‫ج‬‫ل‬‫ا‬ ‫ر‬‫ي‬‫د‬‫ق‬‫ت‬
‫س‬ ‫المعادلة‬ ‫ل‬َّ ‫ح‬2
+6+ ‫س‬6=0‫الجذور‬ ‫تكن‬ ‫لم‬ ‫وإذا‬ ،‫يا‬ًّ‫بيان‬
.‫عشرة‬ ‫من‬ ‫جزء‬ ‫لقرب‬ ‫فقدرها‬ ،‫فصحيحة‬ ‫ا‬ً‫أعداد‬
‫س‬ = (‫)س‬ ‫د‬ ‫المرتبطة‬ ‫الدالة‬ ‫مثل‬2
+6+ ‫س‬6.‫يا‬ًّ‫بيان‬
- ‫بين‬ ‫السينيان‬ ‫المقطعان‬ ‫يقع‬5- ،4- ‫وبين‬ ،2- ‫ـ‬1

36. ‫طوله‬ ‫بتدريج‬ ‫ل‬ً ‫جدو‬ ‫أنشئ‬0.1‫بين‬ ‫تقع‬ ‫التي‬ ‫س‬ ‫لقيم‬
-5،4- ‫وبين‬ ،2- ،1‫إشارات‬ ‫في‬ ‫التغير‬ ‫عن‬ ‫وابحث‬
‫هي‬ ‫الصفر‬ ‫إلى‬ ‫القرب‬ ‫الدالة‬ ‫قيمة‬ ‫وتعد‬ ،‫الدالة‬ ‫قيم‬
.‫الدالة‬ ‫لصفر‬ ‫الفضل‬ ‫التقريب‬

37. ‫س‬
‫ص‬
-4,8 -4,9-4,7-4,5 -4,6-4,4-4,2 -4,3-4,1
0,610,24-0,11-0,44-0,75-1,04-1,31-1,56-1,79

38. ‫س‬
‫ص‬
-1,8 -1,9-1,7-1,5 -1,6-1,4-1,2 -1,3-1,1
1,791,56-1,31-1,04-0,75-1,44-0,11-1,24-0,61

39. ‫تغير‬ ‫عند‬ ‫الصفر‬ ‫إلى‬ ‫الرقرب‬ ‫الدالة‬ ‫رقيمة‬ ‫أن‬ ‫بما‬
‫هي‬ ‫الجدولين‬ ‫كل‬ ‫في‬ ‫الاشارة‬-0,11‫فإن‬ ‫لذا‬ ،
:‫هما‬ ‫التقريبيين‬ ‫الجذرين‬-4,7،-1,3

40. ‫فهمك‬ ‫من‬ ‫تحقق‬
4‫المعادلة‬ ‫حل‬ (2‫س‬2+6– ‫س‬3=0
،‫صحيحة‬ ‫أعداد‬ ‫الجذور‬ ‫تكن‬ ‫لم‬ ‫وإذا‬ .‫يا‬ًّ‫بيان‬
.‫عشرة‬ ‫من‬ ‫جزء‬ ‫لرقرب‬ ‫درها‬ّ‫ر‬‫فق‬
0,4- ،3,4

41. ‫فهمك‬ ‫من‬ ‫تحقق‬
‫البياني‬ ‫للتمثيل‬ ‫السينيين‬ ‫المقطعين‬ ‫تقريب‬ ‫د‬ّ‫ر‬‫يع‬ُ
‫وارقع‬ ‫من‬ ‫تطبيقات‬ ‫في‬ ‫ا‬ً ‫مفيد‬ ‫التربيعية‬ ‫للدوال‬
.‫الحياة‬

42. ‫ل‬‫ا‬‫ث‬‫م‬5
‫ة‬‫ا‬‫ي‬‫ح‬‫ل‬‫ا‬ ‫ع‬‫رق‬‫ا‬‫و‬ ‫ن‬‫م‬
:
:‫البيانية‬ ‫الحاسبة‬ ‫باستعمال‬ ‫الجذور‬ ‫تقدير‬
‫بسرعة‬ ‫العلى‬ ‫إلى‬ ‫الرض‬ ‫من‬ ‫واحدة‬ ‫رقدم‬ ‫ارتفاع‬ ‫من‬ ‫بقدمه‬ ‫الكرة‬ ‫سميح‬ ‫رقذف‬65/‫رقدم‬
- = ‫ع‬ ‫الدالة‬ ‫وتمثل‬ ،‫ثانية‬16‫ن‬2
+65+ ‫ن‬1،‫ثانية‬ ‫ن‬ ‫بعد‬ ‫بالرقدام‬ ‫ع‬ ‫الكرة‬ ‫ارتفاع‬
‫ا ؟‬ً ‫تقريب‬ ‫الهواء‬ ‫في‬ ‫الكرة‬ ‫تبقى‬ ‫فكم‬
- ‫المعادلة‬ ‫جذور‬ ‫ليجاد‬16‫ن‬2
+65+ ‫ن‬1=0‫تمثيل‬ ‫في‬ ‫البيانية‬ ‫الحاسبة‬ ‫استعمل‬ ،
- = (‫)س‬ ‫د‬ ‫المرتبطة‬ ‫الدالة‬16‫ن‬2
+65+ ‫ن‬1‫الموجب‬ ‫السيني‬ ‫المقطع‬ ‫أن‬ ‫بما‬
‫هو‬ ‫للتمثيل‬4‫بقيت‬ ‫الكرة‬ ‫فإن‬ ‫لذا‬ ،‫ا‬ً ‫تقريب‬4.‫الهواء‬ ‫في‬ ‫ا‬ً ‫تقريب‬ ‫ثوان‬

43. 5‫من‬ ‫رقدمين‬ ‫ارتفاع‬ ‫من‬ ‫الكرة‬ ‫سميح‬ ‫رقذف‬ ‫إذا‬ (
‫بسرعة‬ ‫العلى‬ ‫إلى‬ ‫الرض‬55‫فكم‬ .‫ثانية‬ /‫رقدم‬
‫ا ؟‬ً ‫تقريب‬ ‫الهواء‬ ‫في‬ ‫الكرة‬ ‫تبقى‬

44. ‫تأكد‬
:‫يا‬ًّ‫بيان‬ ‫يأتي‬ ‫فيما‬ ‫معادلة‬ ‫كل‬ ‫حل‬
1‫س‬ (2
+3-‫س‬10=0
≥(‫المدى=}د)س(|د)س‬ ، ‫المجال=ح‬2{ ≥(‫المدى=}د)س(|د)س‬ ، ‫المجال=ح‬2{

45. :‫المسائل‬ ‫وحل‬ ،‫تدرب‬
:‫يا‬ًّ‫ن‬‫يا‬‫ب‬ ‫ي‬‫ت‬‫يأ‬ ‫ا‬‫م‬‫ي‬‫ف‬ ‫ة‬‫دل‬‫عا‬‫م‬ ‫ل‬‫ك‬ ‫ل‬ّ ‫ح‬
9‫س‬ (2
+2– ‫س‬24=0
4- ،6

46. ‫التي‬ ‫المرات‬ ‫عدد‬ ‫لتحديد‬ ‫العوامل‬ ‫إلى‬ ‫التحليل‬ ‫استعمل‬
‫دالة‬ ‫كل‬ ‫في‬ ‫السينات‬ ‫محور‬ ‫البياني‬ ‫التمثيل‬ ‫فيها‬ ‫يقطع‬
:‫منها‬ ‫كل‬ ‫أصفار‬ ‫حدد‬ ‫ثم‬ ،‫يأتي‬ ‫مما‬
15‫س‬ = ‫ص‬ (2
–8+ ‫س‬16
1‫؛‬4
:‫المسائل‬ ‫وحل‬ ،‫تدرب‬

47. ‫التي‬ ‫المرات‬ ‫عدد‬ ‫لتحديد‬ ‫العوامل‬ ‫إلى‬ ‫التحليل‬ ‫استعمل‬
‫دالة‬ ‫كل‬ ‫في‬ ‫السينات‬ ‫محور‬ ‫البياني‬ ‫التمثيل‬ ‫فيها‬ ‫يقطع‬
:‫منها‬ ‫كل‬ ‫أصفار‬ ‫حدد‬ ‫ثم‬ ،‫يأتي‬ ‫مما‬
17‫س‬ = ‫ص‬ (2
+12+ ‫س‬32
2- ‫؛‬4- ،8
:‫المسائل‬ ‫وحل‬ ،‫تدرب‬

48. ‫الدرس‬ ‫انتهى‬