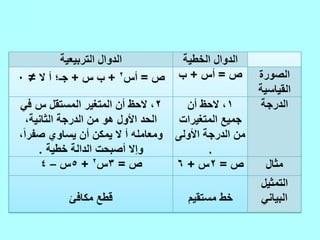
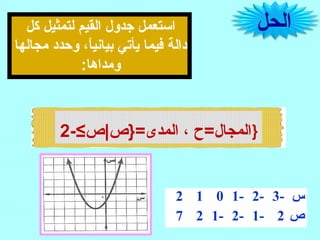
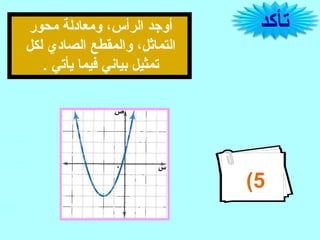
تتناول الوثيقة موضوع تمثيل الدوال التربيعية، حيث تشرح خصائص الدوال التربيعية وخطوط تماثلها، وطرق تحديد القيم العظمى والصغرى عبر معادلاتها. بالإضافة إلى ذلك، تقدم الوثيقة أمثلة عملية باستخدام الجداول البيانية لتوضيح المفاهيم. يتضمن الشرح كيفية إيجاد المواضع الأساسية للدوال التربيعية مثل رأس الدالة ونقطة التقاء المحور الصادي.

1. 8-1‫الدوال‬ ‫تمثيل‬ :
‫ا‬ً‫بياني‬ ‫التربيعية‬

2. :‫سبق‬ ‫فيما‬
. ‫ا‬ً‫بياني‬ ‫الخطية‬ ‫الدوال‬ ‫تمثيل‬ ‫درست‬
‫والن‬
‫البيانية‬ ‫التمثيل ت‬ ‫أحلل‬ -
. ‫التربيعية‬ ‫للدوال‬

3. :‫سبق‬ ‫فيما‬
. ‫ا‬ً‫بياني‬ ‫الخطية‬ ‫الدوال‬ ‫تمثيل‬ ‫درست‬
‫والن‬
‫التربيعية‬ ‫الدوال‬ ‫أمثل‬ -
. ‫ا‬ً‫بياني‬

4. -‫الخطية‬ ‫غير‬ ‫الدالة‬
-‫التربيعية‬ ‫الدالة‬
‫المكافئ‬ ‫القطع‬ -
‫القياسية‬ ‫الصورة‬ -
‫التماثل‬ ‫محور‬ -
‫الرأس‬ -
‫الصغرى‬ ‫القيمة‬ -
‫العظمى‬ ‫القيمة‬ -
‫متماثل‬ -
‫المفردا ت‬

5. ‫لماذا؟‬
‫جدة‬ ‫في‬ ‫فهد‬ ‫الملك‬ ‫نافورة‬ ‫تعد‬ُ
‫في‬ ‫نوعها‬ ‫من‬ ‫نافورة‬ ‫أعلى‬
‫إلى‬ ‫ارتفاعها‬ ‫يصل‬ ‫إذ‬ ،‫العالم‬
312‫ا‬ً‫عرض‬ ‫وتقدم‬ ،‫ا‬ً‫متر‬
،‫والضوء‬ ‫المياه‬ ‫لحركة‬ ‫ا‬ً‫رائع‬

6. ‫لماذا؟‬
‫المياه‬ ‫حركة‬ ‫تمثيل‬ ‫ويمكن‬
‫يمكنك‬ ‫كما‬ .‫تربيعية‬ ‫بمعادل ت‬
‫البيانية‬ ‫التمثيل ت‬ ‫استعمال‬
‫مسار‬ ‫لتوضيح‬ ‫المعادل ت‬ ‫لهذه‬
. ‫المياه‬

7. :‫التربيعية‬ ‫الدوال‬ ‫خصائص‬
‫ا‬ً‫أيض‬ ‫وهناك‬ ،‫الخطية‬ ‫الدوال‬ ‫ا‬ً‫سابق‬ ‫درست‬
‫خطية‬ ‫غير‬ ‫دوال‬‫تمثيلتها‬ ‫أشكال‬ ‫تختلف‬
.‫البيانية‬‫التربيعية‬ ‫فالدوال‬‫غير‬ ‫دوال‬ ‫هي‬ ‫ل‬ً ‫مث‬
‫الصورة‬ ‫على‬ ‫كتابتها‬ ‫ويمكن‬ ‫خطية‬
‫أس‬ = (‫)س‬ ‫د‬2
،‫جـ‬ + ‫س‬ ‫ب‬ +‫أ‬ ‫حيث‬≠0

8. ‫الصورة‬ ‫هذه‬ ‫تسمى‬ُ‫و‬‫القياسية‬ ‫بالصورة‬
‫البياني‬ ‫التمثيل‬ ‫ويسمى‬ ‫التربيعية‬ ‫للدالة‬
‫التربيعية‬ ‫للدالة‬‫ا‬ً‫مكافئ‬ ‫ا‬ً‫قطع‬‫القطوع‬ ‫وتتماثل‬ .
‫يسمى‬ ‫يتوسطها‬ ‫خط‬ ‫حول‬ ‫المكافئة‬‫محور‬
‫التماثل‬‫تسمى‬ ‫واحدة‬ ‫نقطة‬ ‫في‬ ‫القطع‬ ‫يقطع‬ ،
‫الرأس‬.

9. ‫أساسي‬ ‫مفهوم‬
‫التربيعية‬ ‫الدوال‬
‫س‬ = (‫)س‬ ‫د‬2
‫)الم‬ ‫المولدة‬ ‫:)الدالة‬
‫القياسية‬ ‫:الصورة‬
‫أس‬ = (‫)س‬ ‫د‬2
+‫ج‬ + ‫س‬ ‫ب‬‫ـ‬
‫التمثيل‬ ‫:شكل‬
‫مكافئ‬ ‫قطع‬

10. - = ‫س‬‫ــــــــ‬
‫التماثل‬ ‫:محور‬
‫ب‬
2‫أ‬
‫الصادي‬ ‫:المقطع‬
‫جـ‬

11. ‫أس‬ = ‫ص‬ ‫للدالة‬ ‫البياني‬ ‫التمثيل‬ ‫ويكون‬2
‫جـ‬ + ‫س‬ ‫ب‬ +
‫أ‬ ‫كان‬ ‫إذا‬ ،‫العلى‬ ‫إلى‬ ‫ا‬ً‫مفتوح‬0‫فيه‬ ‫نقطة‬ ‫أدنى‬ ‫وتمثل‬ ،
‫كان‬ ‫إذا‬ ،‫السفل‬ ‫إلى‬ ‫ا‬ً‫مفتوح‬ ‫ويكون‬ ،‫الصغرى‬ ‫القيمة‬ ‫نقطة‬
‫أ‬0‫وتمثل‬ ،‫العظمى‬ ‫القيمة‬ ‫نقطة‬ ‫فيه‬ ‫نقطة‬ ‫أعلى‬ ‫وتمثل‬
. ‫القطع‬ ‫رأس‬ ‫الصغرى‬ ‫القيمة‬ ‫أو‬ ‫العظمى‬ ‫القيمة‬ ‫نقطتي‬

12. ‫والمدى‬ ‫المجال‬
‫القيم‬ ‫جميع‬ ‫مجموعة‬ ‫هو‬ ‫المجال‬
‫وأما‬ .‫س‬ ‫المستقل‬ ‫للمتغير‬ ‫الممكنة‬
‫القيم‬ ‫جميع‬ ‫مجموعة‬ ‫فهو‬ ‫المدى‬
‫ص‬ ‫التابع‬ ‫للمتغير‬ ‫.الممكنة‬

13. ‫المكافئ‬ ‫للقطع‬ ‫البياني‬ ‫التمثيل‬
‫مثال‬1
‫الدالة‬ ‫لتمثيل‬ ‫القيم‬ ‫جدول‬ ‫استعمل‬
= ‫ص‬3‫س‬2
+6– ‫س‬4. ‫ومداها‬ ‫مجالها‬ ‫وحدد‬ ،‫ا‬ً‫بياني‬

15. ‫الحــــــــــــــــــــــل‬

16. ‫ص‬ ‫س‬
5 1
-4 0
-7 -1
-4 -2
5 -3
‫ويمتد‬ .‫أملس‬ ‫بمنحنى‬ ‫بينها‬ ‫وصل‬ ‫ثم‬ ،‫ا‬ً‫بياني‬ ‫المرتبة‬ ‫الوزواج‬ ‫مثل‬
،‫طرفيه‬ ‫كل‬ ‫من‬ ‫نهاية‬ ‫ل‬ ‫ما‬ ‫إلى‬ ‫المكافئ‬ ‫للقطع‬ ‫البياني‬ ‫التمثيل‬
‫هو‬ ‫ومداه‬ ،‫الحقيقية‬ ‫العداد‬ ‫جميع‬ ‫هو‬ ‫ومجاله‬
‫}ص‬|-≤‫ص‬ ،7- ‫لن‬ ‫{؛‬7. ‫الصغرى‬ ‫القيمة‬ ‫هي‬

17. ‫ص‬ ‫س‬
5 1
-4 0
-7 -1
-4 -2
5 -3
‫بمنحنى‬ ‫بينها‬ ‫وصل‬ ‫ثم‬ ،‫ا‬ً‫بياني‬ ‫المرتبة‬ ‫الوزواج‬ ‫مثل‬
‫ل‬ ‫ما‬ ‫إلى‬ ‫المكافئ‬ ‫للقطع‬ ‫البياني‬ ‫التمثيل‬ ‫ويمتد‬ .‫أملس‬
،‫طرفيه‬ ‫كل‬ ‫من‬ ‫نهاية‬

18. ‫فهمك‬ ‫من‬ ‫تحقق‬
1‫الدالة‬ ‫لتمثيل‬ ‫القيم‬ ‫جدول‬ ‫استعمل‬ (
‫س‬ = ‫ص‬2
+3‫وحدد‬ ،‫ا‬ً‫بياني‬
. ‫ومداها‬ ‫مجالها‬

20. ‫الحــــــــــــــــــــــل‬

21. ‫الــــحل‬ :
≤‫=}ص|ص‬ ‫المدى‬ ، ‫المجال=ح‬3 }

22. ‫الشكال‬‫المتماثلة‬‫التي‬ ‫الشكال‬ ‫تلك‬ ‫هي‬
‫فالقطع‬ .‫ا‬ً‫تمام‬ ‫متطابقين‬ ‫نصفاها‬ ‫يكون‬
‫محور‬ ‫وله‬ ‫متماثل‬ ‫شكل‬ ‫هو‬ ‫المكافئ‬
‫إلى‬ ‫القطع‬ ‫نصف‬ ‫في‬ ‫نقطة‬ ‫وكل‬ ،‫متماثل‬
‫في‬ ‫نقطة‬ ‫تقابلها‬ ‫التماثل‬ ‫محور‬ ‫يسار‬
. ‫له‬ ‫الخر‬ ‫النصف‬

23. ‫إيجاد‬ ‫عند‬ ‫عادة‬ ‫السهل‬ ‫من‬ ‫ويكون‬
‫تحديد‬ ،‫البياني‬ ‫التمثيل‬ ‫من‬ ‫الخصائص‬
‫عظمى‬ ‫نقطة‬ ‫إما‬ ‫يمثل‬ ‫والذي‬ ،‫ل‬ً ‫أو‬ ‫الرأس‬
. ‫للقطع‬ ‫صغرى‬ ‫نقطة‬ ‫أو‬

24. ‫من‬ ‫المكافئ‬ ‫القطع‬ ‫خصائص‬ ‫تحديد‬
‫البياني‬ ‫تمثيله‬
‫مثال‬2
‫والمقطع‬ ،‫التماثل‬ ‫محور‬ ‫ومعادلة‬ ،‫الرأس‬ ‫أوجد‬
:‫التالي‬ ‫البياني‬ ‫للتمثيل‬ ‫الصادي‬

25. ‫الخطوة‬1:
.‫الس‬ ‫أوجد‬
‫السفل‬ ‫إلى‬ ‫مفتوح‬ ‫المكافئ‬ ‫المقطع‬ ‫أن‬ ‫بما‬
) ‫وهي‬ ‫له‬ ‫العظمى‬ ‫النقطة‬ ‫يمثل‬ ‫فالرأس‬2،3. (

26. ‫الخطوة‬2:
. ‫التماثل‬ ‫محور‬ ‫أوجد‬
‫بالرأس‬ ‫يمر‬ ‫الذي‬ ‫المستقيم‬ ‫هو‬ ‫التماثل‬ ‫محور‬ ‫أن‬ ‫بما‬
‫محور‬ ‫معادلة‬ ‫تكون‬ ‫لذا‬ ،‫متطابقين‬ ‫نصفين‬ ‫إلة‬ ‫القطع‬ ‫ويقسم‬
= ‫س‬ ‫هي‬ ‫التماثل‬2.

27. ‫الخطوة‬3:
.‫الصادي‬ ‫المقطع‬ ‫أوجد‬
‫القطع‬ ‫فيها‬ ‫يتقاطع‬ ‫التي‬ ‫النقطة‬ ‫هو‬ ‫الصادي‬ ‫المقطع‬ ‫أن‬ ‫بما‬
) ‫النقطة‬ ‫وهي‬ ،‫الصادات‬ ‫محور‬ ‫مع‬ ‫المكافئ‬0- ،1‫لذا‬ ،(
- ‫هو‬ ‫الصادي‬ ‫المقطع‬ ‫يكون‬1.

28. ‫الدرس‬ ‫موضوع‬‫التربيعية‬ ‫الدوال‬ ‫تمثيل‬
‫بيــــــــــــــــــــــــــــــــــانيا‬
: ‫س‬‫والمقطع‬ ‫التماثل‬ ‫محور‬ ‫ومعادلة‬ ‫الرأس‬ ‫أوجدي‬
( ‫أ‬ ) : ‫التالي‬ ‫البياني‬ ‫للتمثيل‬ ‫الصادي‬
00000000000000000000000000000000000000000000000000000000
: ‫س‬‫والمقطع‬ ‫التماثل‬ ‫محور‬ ‫ومعادلة‬ ‫الرأس‬ ‫أوجدي‬
‫ــ‬ = ‫ص‬ : ‫للدالة‬ ‫الصادي‬3‫س‬2+6‫ــ‬ ‫س‬5
‫ابراهيم‬ ‫نجل ء‬ ‫م‬
‫عمــــــــــــــل‬ ‫ورقـــــــــــــة‬

29. ‫فهمك‬ ‫من‬ ‫تحقق‬
2(‫أ‬

30. ‫الحــــــل‬
-)= ‫الرأس‬1،3‫التماثل‬ ‫محور‬ ، (
-=‫س‬1= ‫الصادي‬ ‫المقطع‬ ،2

31. ‫الدرس‬ ‫موضوع‬‫التربيعية‬ ‫الدوال‬ ‫تمثيل‬
‫بيــــــــــــــــــــــــــــــــــانيا‬
: ‫س‬‫والمقطع‬ ‫التماثل‬ ‫محور‬ ‫ومعادلة‬ ‫الرأس‬ ‫أوجدي‬
( ‫ب‬ ) : ‫التالي‬ ‫البياني‬ ‫للتمثيل‬ ‫الصادي‬
00000000000000000000000000000000000000000000000000000000
: ‫س‬‫والمقطع‬ ‫التماثل‬ ‫محور‬ ‫ومعادلة‬ ‫الرأس‬ ‫أوجدي‬
‫ــ‬ = ‫ص‬ : ‫للدالة‬ ‫الصادي‬3‫س‬2+6‫ــ‬ ‫س‬5
‫ابراهيم‬ ‫نجل ء‬ ‫م‬
‫عمــــــــــــــل‬ ‫ورقـــــــــــــة‬

32. ‫فهمك‬ ‫من‬ ‫تحقق‬
2(‫ب‬

33. ‫الحــــل‬
)= ‫الرأس‬1،3‫التماثل‬ ‫محور‬ ، (
=‫س‬1= ‫الصادي‬ ‫المقطع‬ ،4

34. ‫المكافئ‬ ‫القطع‬ ‫خصائص‬ ‫تحديد‬ ‫عند‬
‫الهسهل‬ ‫من‬ ‫ا‬ً ‫فغالب‬ ‫الدالة‬ ‫قاعدة‬ ‫من‬
. ‫ال‬ً ‫أو‬ ‫التماثل‬ ‫محور‬ ‫معادلة‬ ‫إيجاد‬

35. ‫الصادي‬ ‫المقطع‬
‫الصادي‬ ‫للمقطع‬ ‫الصادي‬ ‫الدحداثي‬
‫للدالة‬ (‫)جـ‬ ‫الثابت‬ ‫الحد‬ ‫هو‬
‫القياهسية‬ ‫الصورة‬ ‫في‬ ‫التربيعية‬

36. ‫من‬ ‫المكافئ‬ ‫القطع‬ ‫خصائص‬ ‫تحديد‬
‫دالته‬ ‫قاعدة‬
‫مثال‬3
‫والمقطع‬ ،‫التماثل‬ ‫محور‬ ‫ومعادلة‬ ،‫الرأس‬ ‫أوجد‬
= ‫ص‬ :‫للدالة‬ ‫الصادي‬2‫س‬2
+4– ‫س‬3.

37. ‫الحـــل‬
- = ‫س‬‫ـــــــــ‬
‫ب‬
2‫أ‬
‫التماثل‬ ‫محور‬ ‫معادلة‬ ‫صيغة‬
- = ‫س‬- =‫س‬ ‫ـــــــــ‬1
4
2×2
= ‫أ‬2= ‫ب‬ ،4‫بسط‬ ،
- = ‫س‬ ‫هي‬ ‫التماثل‬ ‫محور‬ ‫معادلة‬1.

38. ‫محور‬ ‫معادلة‬ ‫من‬ ‫الناتجة‬ ‫القيمة‬ ‫خذ‬ ،‫الرأس‬ ‫إدحداثي‬ ‫وليجاد‬
‫ثم‬ ‫المكافئ‬ ‫القطع‬ ‫لرأس‬ ‫ا‬ً ‫هسيني‬ ‫ا‬ً ‫إدحداثي‬ ‫واعتبرها‬ ،‫التماثل‬
. ‫الصادي‬ ‫الدحداثي‬ ‫ليجاد‬ ‫المكافئ‬ ‫القطع‬ ‫معادلة‬ ‫في‬ ‫عوضها‬
= ‫ص‬2‫س‬2
+4‫س‬–3‫الصلية‬ ‫المعادلة‬
= 2 (-1)2
+ 4 (-1) – 3 = -5
- = ‫س‬1‫بسط‬ ،
-) ‫هو‬ ‫الرأس‬1- ،5‫عند‬ ‫هو‬ ‫الصادي‬ ‫المقطع‬ ‫أن‬ ‫وبما‬ ،(
) ‫النقطة‬0‫ج‬ ،‫ـ‬- ‫هو‬ ‫الصادي‬ ‫فالمقطع‬ ‫لذا‬ ،‫ا‬ً ‫دائم‬ (3.

39. ‫الدرس‬ ‫موضوع‬‫التربيعية‬ ‫الدوال‬ ‫تمثيل‬
‫بيــــــــــــــــــــــــــــــــــانيا‬
: ‫س‬‫والمقطع‬ ‫التماثل‬ ‫محور‬ ‫ومعادلة‬ ‫الرأس‬ ‫أوجدي‬
( ‫ب‬ ) : ‫التالي‬ ‫البياني‬ ‫للتمثيل‬ ‫الصادي‬
00000000000000000000000000000000000000000000000000000000
: ‫س‬‫والمقطع‬ ‫التماثل‬ ‫محور‬ ‫ومعادلة‬ ‫الرأس‬ ‫أوجدي‬
‫ــ‬ = ‫ص‬ : ‫للدالة‬ ‫الصادي‬3‫س‬2+6‫ــ‬ ‫س‬5
‫ابراهيم‬ ‫نجل ء‬ ‫م‬
‫عمــــــــــــــل‬ ‫ورقـــــــــــــة‬

40. ‫فهمك‬ ‫من‬ ‫تحقق‬
3- = ‫ص‬ (‫أ‬3‫س‬2
+6– ‫س‬5

41. ‫الحـــــل‬
)= ‫الرأس‬1-،2‫التماثل‬ ‫محور‬ ، (
=‫س‬1-= ‫الصادي‬ ‫المقطع‬ ،5

42. ‫فهمك‬ ‫من‬ ‫تحقق‬
3= ‫ص‬ (‫ب‬2‫س‬2
+2+ ‫س‬2

43. ‫الحــــــل‬
-)= ‫الرأس‬1/2،3/2‫التماثل‬ ‫محور‬ ، (
-=‫س‬1/2= ‫الصادي‬ ‫المقطع‬ ،2

44. ‫الدوال‬ ‫بين‬ ‫عامة‬ ‫فروق‬ ‫هناك‬
‫في‬ ‫تظهر‬ ‫التربيعية‬ ‫والدوال‬ ‫الخطية‬
:‫التي‬ ‫الجدول‬

46. ‫المكافئ‬ ‫القطع‬ ‫كان‬ ‫إن‬ ‫تحدد‬ ‫كيف‬
،‫الهسفل‬ ‫إلى‬ ‫أم‬ ‫العلى‬ ‫إلى‬ ‫ا‬ً ‫مفتودح‬
‫نقطة‬ ‫له‬ ‫يمثل‬ ‫الرأس‬ ‫كان‬ ‫وإذا‬
‫عظمى؟‬ ‫نقطة‬ ‫أم‬ ‫صغرى‬

47. ‫أهساهسي‬ ‫مفهوم‬
‫الصغرى‬ ‫والقيم‬ ‫العظمى‬ ‫القيم‬
:‫اللفظي‬ ‫التعبير‬‫د‬ :‫للدالة‬ ‫البياني‬ ‫التمثيل‬ ‫يكون‬
‫أس‬ = (‫)س‬2
‫أ‬ ‫دحيث‬ ،‫جـ‬ + ‫س‬ ‫ب‬ +≠0 :
‫أ‬ ‫عندما‬ ‫عظمى‬ ‫قيمة‬ ‫وله‬ ‫الهسفل‬ ‫إلى‬ ‫ا‬ً ‫مفتودح‬ -0
‫أ‬ ‫عندما‬ ‫صغرى‬ ‫قيمة‬ ‫وله‬ ‫العلى‬ ‫إلى‬ ‫ا‬ً ‫مفتودح‬ -0
‫الحقيقية‬ ‫العداد‬ ‫جميع‬ ‫هو‬ ‫التربيعية‬ ‫الدالة‬ ‫مدى‬ -
‫كانت‬ ‫إذا‬ ‫الصغرى‬ ‫القيمة‬ ‫تساوي‬ ‫أو‬ ‫على‬ ‫تزيد‬ ‫التي‬
‫أ‬0‫أو‬ ‫عن‬ ‫تقل‬ ‫التي‬ ‫الحقيقية‬ ‫العداد‬ ‫جميع‬ ‫أو‬ ،
‫أ‬ ‫كانت‬ ‫إذا‬ ‫العظمى‬ ‫القيمة‬ ‫تساوي‬0

48. ‫أهساهسي‬ ‫مفهوم‬‫العظمى‬ ‫القيم‬
‫الصغرى‬ ‫والقيم‬

49. ‫العظمى‬ ‫والقيم‬ ‫الصغرى‬ ‫القيم‬
‫السيني‬ ‫الدحداثيين‬ ‫كل‬ ‫إيجاد‬ ‫تنس‬ ‫ال‬
‫دحيث‬ (‫ص‬ ،‫)س‬ ‫للرأس‬ ‫والصادي‬
‫القيمة‬ ‫أو‬ ‫الصغرى‬ ‫القيمة‬ ‫أن‬
‫له‬ ‫الصادي‬ ‫الدحداثي‬ ‫تمثل‬ ‫.العظمى‬

50. ‫ل‬‫ا‬‫ث‬‫م‬4
‫الصغرى‬ ‫والقيم‬ ‫العظمى‬ ‫القيم‬
- = (‫)س‬ ‫د‬ ‫لتكن‬2‫س‬2
–4+ ‫س‬6.
‫قيمة‬ ‫للدالة‬ ‫كان‬ ‫إذا‬ ‫دحدد‬ (‫أ‬
. ‫صغرى‬ ‫قيمة‬ ‫أم‬ ‫عظمى‬
- = (‫)س‬ ‫د‬ ‫الدالة‬ ‫في‬2‫س‬2
–4+ ‫س‬6،
- = ‫أ‬2- = ‫ب‬ ،4= ‫جـ‬ ،6.

51. ‫الحــــــــل‬
- = (‫)س‬ ‫د‬ ‫الدالة‬ ‫في‬2‫س‬2
–4+ ‫س‬6،
- = ‫أ‬2- = ‫ب‬ ،4= ‫جـ‬ ،6.
‫يكون‬ ‫البياني‬ ‫فالتمثيل‬ ‫سالب‬ ‫عدد‬ ‫أ‬ ‫أن‬ ‫بما‬
‫عظمى‬ ‫قيمة‬ ‫للدالة‬ ‫ويكون‬ ،‫السفل‬ ‫إلى‬ ‫ا‬ً ‫مفتوح‬

52. ‫أو‬ ‫العظمى‬ ‫القيمة‬ ‫أوجد‬ (‫ب‬
. ‫للدالة‬ ‫الصغرى‬ ‫القيمة‬
‫الصادي‬ ‫الحداثي‬ ‫هي‬ ‫العظمى‬ ‫القيمة‬
. ‫للرأس‬
‫يساوي‬ ‫للرأس‬ ‫السيني‬ ‫الحداثي‬= ‫ـــــــ‬
‫ــــــــــــــــ‬- =1. 4
2-)2(
‫-ب‬
2‫أ‬
) ‫د‬‫س‬- = (2‫س‬2
–4‫س‬+6‫اللصلية‬ ‫الدالة‬

53. ) ‫د‬-1- = (2-)1(2
–4-)1(+6- = ‫س‬1
) ‫د‬-1= (8
‫تساوي‬ ‫العظمى‬ ‫القيمة‬ ،‫إذن‬8.
‫ج‬‫ـ‬. ‫ومداها‬ ‫الدالة‬ ‫مجال‬ ‫حدد‬ (
‫جميع‬ ‫هو‬ ‫والمدى‬ ،‫الحقيقية‬ ‫العداد‬ ‫جميع‬ ‫هو‬ ‫المجال‬
،‫العظمى‬ ‫القيمة‬ ‫تساوي‬ ‫أو‬ ‫عن‬ ‫تقل‬ ‫التي‬ ‫الحقيقية‬ ‫العداد‬
‫}ص‬ ‫أي‬|≥ ‫ص‬ ،8. {

54. ‫الدرس‬ ‫موضوع‬‫التربيعية‬ ‫الدوال‬ ‫تمثيل‬ ‫تابع‬
= ( ‫س‬ )‫د‬ ‫ليكن‬ : ‫س‬2‫س‬2‫ــ‬4‫ــ‬ ‫س‬1
*‫صغرى‬ ‫قيمة‬ ‫أم‬ ‫عظمى‬ ‫قيمة‬ ‫للدالة‬ ‫كان‬ ‫اذا‬ ‫فيما‬ ‫حدد‬0
*‫الصغرى‬ ‫القيمة‬ ‫أو‬ ‫العظمى‬ ‫القيمة‬ ‫أوجد‬
‫للدالة‬0
*‫ومداها‬ ‫الدالة‬ ‫مجال‬ ‫حدد‬0
0000000000000000000000000000000000000000000000000000000000000000000000000000000
000000000000
‫س‬:=( )‫س‬ ‫د‬ ‫الدالة‬ ‫مثل‬3‫س‬2‫ـ‬6+ ‫س‬2
‫بيانيا‬
‫عـــــــــــمل‬ ‫ورقــــــــــة‬

55. ‫فهمك‬ ‫من‬ ‫تحقق‬
4‫قيمة‬ ‫للدالة‬ ‫كان‬ ‫إذا‬ ‫فيما‬ ‫حدد‬ (‫أ‬
. ‫لصغرى‬ ‫قيمة‬ ‫أم‬ ‫عظمى‬
= (‫)س‬ ‫د‬ ‫ليكن‬2‫س‬2
–4– ‫س‬1.

56. ‫لصغري‬ ‫قيمة‬
‫الحـــــل‬

57. 4‫القيمة‬ ‫أو‬ ‫العظمى‬ ‫القيمة‬ ‫أوجد‬ (‫ب‬
. ‫للدالة‬ ‫الصغرى‬

58. - =3
‫الحـــــل‬

59. 4‫ج‬‫ـ‬‫ومداها‬ ‫الدالة‬ ‫مجال‬ ‫حدد‬ (

60. ، ‫المجال=ح‬
-≤‫المدى=}ص|ص‬3{
‫الحـــــل‬

61. : ‫ا‬ً ‫بياني‬ ‫التربيعية‬ ‫الدوال‬ ‫تمثيل‬‫تعلمت‬
‫الخصائص‬ ‫من‬ ‫العديد‬ ‫إيجاد‬ ‫كيفية‬
. ‫التربيعية‬ ‫للدوال‬ ‫الهامة‬

62. ‫أساسي‬ ‫مفهوم‬
‫الدوال‬ ‫تمثيل‬
‫ا‬ً ‫بياني‬ ‫التربيعية‬
‫الخطوة‬1
. ‫التماثل‬ ‫محور‬ ‫معادلة‬ ‫أوجد‬

63. ‫الخطوة‬2
‫يمثل‬ ‫كان‬ ‫إذا‬ ‫وحدد‬ ‫الرأس‬ ‫أوجد‬
. ‫عظمى‬ ‫نقطة‬ ‫أم‬ ‫لصغرى‬ ‫نقطة‬

64. ‫الخطوة‬3
. ‫الصادي‬ ‫المقطع‬ ‫أوجد‬

65. ‫الخطوة‬4
‫على‬ ‫أخرى‬ ‫نقطة‬ ‫ليجاد‬ ‫التماثل‬ ‫استعمل‬
. ‫الضرورة‬ ‫عند‬ ‫للدالة‬ ‫البياني‬ ‫التمثيل‬

66. ‫الخطوة‬5
. ‫أملس‬ ‫بمنحنى‬ ‫النقاط‬ ‫بين‬ ‫لصل‬

67. ‫والنقاط‬ ‫:التماثل‬
‫الطرفين‬ ‫على‬ ‫الواقعة‬ ‫النقاط‬
‫تبعد‬ ‫التماثل‬ ‫لمحور‬ ‫المتقابلين‬
‫ا‬ً ‫يمين‬ ‫المحور‬ ‫عن‬ ‫نفسها‬ ‫المسافة‬
‫من‬ ‫ا‬ً ‫متساوي‬ ‫ا‬ً ‫بعد‬ ‫تبعد‬ ‫كما‬ ،‫ا‬ً ‫ويسار‬
‫.الرأس‬

68. ‫ل‬‫ا‬‫ث‬‫م‬5
‫ا‬ً ‫بياني‬ ‫التربيعية‬ ‫الدوال‬ ‫تمثيل‬
‫الدالة‬ ‫مثل‬=(‫د)س‬‫س‬2
+4+ ‫س‬3. ‫ا‬ً ‫بياني‬
‫الخطوة‬1: ‫محور‬ ‫معادلة‬ ‫أوجد‬
. ‫التماثل‬
= ‫س‬‫ــــــــ‬-‫ب‬
2‫أ‬
‫معادلة‬ ‫لصيغة‬
‫التماثل‬ ‫محور‬

69. = ‫س‬‫ــــــــ‬
-4
2×1
= ‫أ‬1= ‫ب‬ ،4
= ‫س‬-2‫بسط‬

70. ‫الخطوة‬2: ‫كان‬ ‫إذا‬ ‫فيما‬ ‫وحدد‬ ،‫الرأس‬ ‫أوجد‬
. ‫عظمى‬ ‫أم‬ ‫لصغرى‬ ‫نقطة‬ ‫يمثل‬
= ‫ص‬‫س‬2
+4‫س‬+3‫اللصلية‬ ‫المعادلة‬

71. ) =-2(2
+4)-2+ (3- = ‫س‬2
=-1‫بسط‬
-) ‫النقطة‬ ‫عند‬ ‫الرأس‬ ‫يقع‬2- ،1‫موجبة‬ ‫أ‬ ‫أن‬ ‫وبما‬ ،(
‫قيمة‬ ‫الرأس‬ ‫يمثل‬ ‫لذا‬ ،‫العلى‬ ‫إلى‬ ‫ا‬ً ‫مفتوح‬ ‫يكون‬ ‫فالتمثيل‬
. ‫عظمى‬

72. ‫الخطوة‬3: . ‫الصادي‬ ‫المقطع‬ ‫أوجد‬
= ‫ص‬‫س‬2
+4‫س‬+3‫اللصلية‬ ‫المعادلة‬

73. =)0(2
+4)0(+3- ‫س‬0
‫يساوي‬ ‫الصادي‬ ‫المقطع‬3.
=3‫سط‬ّ‫ط‬ ‫ب‬

74. ‫ل‬‫ا‬‫ث‬‫م‬5‫ا‬ً ‫بياني‬ ‫التربيعية‬ ‫الدوال‬ ‫تمثيل‬
‫الدالة‬ ‫مثل‬=(‫د)س‬‫س‬2
+4+ ‫س‬3. ‫ا‬ً ‫بياني‬
‫الخطوة‬4: ‫القطع‬ ‫التماثل‬ ‫محور‬ ‫يقسم‬
‫لكل‬ ‫فإنه‬ ‫لذا‬ ،‫متطابقين‬ ‫جزأين‬ ‫إلى‬ ‫المكافئ‬
‫نقطة‬ ‫توجد‬ ‫الجزأين‬ ‫أحد‬ ‫على‬ ‫نقطة‬
‫المسافة‬ ‫وتبعد‬ ،‫الخر‬ ‫الجزء‬ ‫في‬ ‫تناظرها‬
‫محور‬ ‫يمثل‬ ‫الذي‬ ‫المستقيم‬ ‫عن‬ ‫نفسها‬
‫نفسه‬ ‫الصادي‬ ‫الحداثي‬ ‫وللنقطتين‬ ،‫التماثل‬
.

75. ‫ل‬‫ا‬‫ث‬‫م‬5‫ا‬ً ‫بياني‬ ‫التربيعية‬ ‫الدوال‬ ‫تمثيل‬
‫الدالة‬ ‫مثل‬=(‫د)س‬‫س‬2
+4+ ‫س‬3. ‫ا‬ً ‫بياني‬
‫الخطوة‬5: ‫النقاط‬ ‫بين‬ ‫لصل‬
. ‫أملس‬ ‫بمنحنى‬

76. ‫الدرس‬ ‫موضوع‬‫التربيعية‬ ‫الدوال‬ ‫تمثيل‬ ‫تابع‬
= ( ‫س‬ )‫د‬ ‫ليكن‬ : ‫س‬2‫س‬2‫ــ‬4‫ــ‬ ‫س‬1
*‫صغرى‬ ‫قيمة‬ ‫أم‬ ‫عظمى‬ ‫قيمة‬ ‫للدالة‬ ‫كان‬ ‫اذا‬ ‫فيما‬ ‫حدد‬0
*‫الصغرى‬ ‫القيمة‬ ‫أو‬ ‫العظمى‬ ‫القيمة‬ ‫أوجد‬
‫للدالة‬0
*‫ومداها‬ ‫الدالة‬ ‫مجال‬ ‫حدد‬0
0000000000000000000000000000000000000000000000000000000000000000000000000000
000000000000000
‫س‬:=( )‫س‬ ‫د‬ ‫الدالة‬ ‫مثل‬3‫س‬2‫ـ‬6+ ‫س‬2
‫بيانيا‬
‫عـــــــــــمل‬ ‫ورقــــــــــة‬

77. ‫فهمك‬ ‫من‬ ‫تحقق‬
5= (‫)س‬ ‫د‬ (‫ب‬3‫س‬2
–6+ ‫س‬2

78. = ‫س‬ ‫التماثل‬ ‫محور‬1
) ‫الرأس‬1‫ــ‬ ،1(
= ‫جـ‬ = ‫الصادي‬ ‫المقطع‬2
‫الحـــــل‬

79. ‫الحــــــــــــــــــــــل‬

80. ‫البياني‬ ‫التمثيل‬

81. = ‫س‬ ‫التمثل‬ ‫محور‬1
) ‫الرأس‬1،6(
= ‫جـ‬ = ‫الصادي‬ ‫المقطع‬3

82. ‫التربيعية‬ ‫الدوال‬ ‫حول‬ ‫معلوماتك‬ ‫استعملت‬
‫تمثيل ت‬ ‫لشنشاء‬ ‫والتماثل‬ ‫المكافئة‬ ‫والقطوع‬
‫لحل‬ ‫التمثيل ت‬ ‫هذه‬ ‫تحليل‬ ‫ويمكنك‬ ،‫بياشنية‬
. ‫الحياة‬ ‫واقع‬ ‫من‬ ‫مسائل‬

83. ‫في‬ ‫الفيزيائية‬ ‫للعلوم‬ ‫السعودية‬ ‫الجمعية‬ ‫أشنشأ ت‬
‫عام‬ ‫خالد‬ ‫الملك‬ ‫جامعة‬1422‫سبل‬ ‫لتهيئة‬ ،‫هـ‬
‫الفيزيائية‬ ‫العلوم‬ ‫بمجال ت‬ ‫المهتمين‬ ‫بين‬ ‫التواصل‬
‫والمؤتمرا ت‬ ‫الندوا ت‬ ‫وتنظيم‬ ‫عقد‬ ‫خلل‬ ‫من‬ ‫المختلفة‬
‫الفيزيائية‬ ‫العلوم‬ ‫مجال‬ ‫.في‬

85. ‫تأكد‬‫كل‬ ‫لتمثيل‬ ‫القيم‬ ‫جدول‬ ‫استعمل‬
‫مجالها‬ ‫وحدد‬ ،‫ا‬ً،‫بياشني‬ ‫يأتي‬ ‫فيما‬ ‫دالة‬
:‫ومداها‬
2‫س‬ = ‫ص‬ (2
+2– ‫س‬1

86. ‫الحل‬‫كل‬ ‫لتمثيل‬ ‫القيم‬ ‫جدول‬ ‫استعمل‬
‫مجالها‬ ‫وحدد‬ ،‫ا‬ً،‫بياشني‬ ‫يأتي‬ ‫فيما‬ ‫دالة‬
:‫ومداها‬
-≤‫المدى=}ص|ص‬ ، ‫المجال=ح‬2 }
2 1 0 -1 -2 -3 ‫س‬
7 2 -1 -2 -1 2 ‫ص‬

87. ‫تأكد‬‫محور‬ ‫ومعادلة‬ ،‫الرأس‬ ‫أوجد‬
‫لكل‬ ‫الصادي‬ ‫والمقطع‬ ،‫التماثل‬
. ‫يأتي‬ ‫فيما‬ ‫بياشني‬ ‫تمثيل‬
4(

88. ‫الحل‬‫محور‬ ‫ومعادلة‬ ،‫الرأس‬ ‫أوجد‬
‫لكل‬ ‫الصادي‬ ‫والمقطع‬ ،‫التماثل‬
. ‫يأتي‬ ‫فيما‬ ‫بياشني‬ ‫تمثيل‬
-)= ‫الرأس‬1،5‫التماثل‬ ‫محور‬ ، (
-=‫س‬1= ‫الصادي‬ ‫المقطع‬ ،3

89. ‫تأكد‬‫محور‬ ‫ومعادلة‬ ،‫الرأس‬ ‫أوجد‬
‫لكل‬ ‫الصادي‬ ‫والمقطع‬ ،‫التماثل‬
. ‫يأتي‬ ‫فيما‬ ‫بياشني‬ ‫تمثيل‬
5(

90. ‫الحل‬‫محور‬ ‫ومعادلة‬ ،‫الرأس‬ ‫أوجد‬
‫لكل‬ ‫الصادي‬ ‫والمقطع‬ ،‫التماثل‬
. ‫يأتي‬ ‫فيما‬ ‫بياشني‬ ‫تمثيل‬
-)= ‫الرأس‬2-،3‫التماثل‬ ‫محور‬ ، (
-=‫س‬2= ‫الصادي‬ ‫المقطع‬ ،1

91. ‫تأكد‬‫محور‬ ‫ومعادلة‬ ،‫الرأس‬ ‫أوجد‬
‫لكل‬ ‫الصادي‬ ‫والمقطع‬ ،‫التماثل‬
:‫يأتي‬ ‫فيما‬ ‫دالة‬
8‫س‬ = ‫ص‬ (2
–4+ ‫س‬5

92. ‫الحل‬‫محور‬ ‫ومعادلة‬ ،‫الرأس‬ ‫أوجد‬
‫لكل‬ ‫الصادي‬ ‫والمقطع‬ ،‫التماثل‬
:‫يأتي‬ ‫فيما‬ ‫دالة‬
)= ‫الرأس‬2،1‫التماثل‬ ‫محور‬ ، (
=‫س‬2= ‫الصادي‬ ‫المقطع‬ ،5

93. ‫المسائل‬ ‫وحل‬ ‫تدرب‬
‫يأتي‬ ‫فيما‬ ‫دالة‬ ‫كل‬ ‫لتمثيل‬ ‫القيم‬ ‫جدول‬ ‫استعمل‬
. ‫ومداها‬ ‫مجالها‬ ‫وحدد‬ ،‫ا‬ً،‫بياشني‬
17) ‫س‬ = ‫ص‬2
+4+ ‫س‬6

94. ‫المسائل‬ ‫وحل‬ ‫تدرب‬
‫يأتي‬ ‫فيما‬ ‫دالة‬ ‫كل‬ ‫لتمثيل‬ ‫القيم‬ ‫جدول‬ ‫استعمل‬
. ‫ومداها‬ ‫مجالها‬ ‫وحدد‬ ،‫ا‬ً،‫بياشني‬
0 -1 -2 -3 -4 ‫س‬
6 3 2 3 6 ‫ص‬
≤‫المدى=}ص|ص‬ ، ‫المجال=ح‬2 }

95. ‫المسائل‬ ‫وحل‬ ‫تدرب‬
‫والمقطع‬ ،‫التماثل‬ ‫محور‬ ‫ومعادلة‬ ‫الرأس‬ ‫أوجد‬
. ‫يأتي‬ ‫فيما‬ ‫بياشني‬ ‫تمثيل‬ ‫لكل‬ ‫الصادي‬
20)

96. ‫المسائل‬ ‫وحل‬ ‫تدرب‬
‫والمقطع‬ ،‫التماثل‬ ‫محور‬ ‫ومعادلة‬ ‫الرأس‬ ‫أوجد‬
. ‫يأتي‬ ‫فيما‬ ‫بياشني‬ ‫تمثيل‬ ‫لكل‬ ‫الصادي‬
-)= ‫الرأس‬3-،6‫التماثل‬ ‫محور‬ ، (
-=‫س‬3= ‫الصادي‬ ‫المقطع‬ ،4