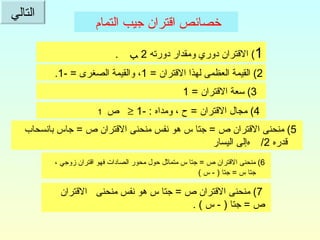
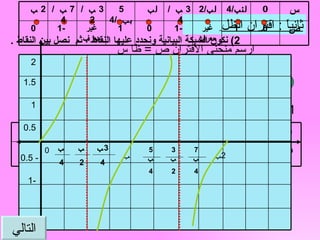
التمثيل البياني للاقترانات المثلثية في الرياضيات لصف العاشر يتضمن دراسة ثلاثة اقترانات رئيسية: الجيب، جيب التمام، والظل، مع توضيح خصائص كل منها مثل الفترات، والقيم العظمى والصغرى، والمجال والمدى. يتم تقديم خطوات لرسم المنحنيات البيانية بتفصيل الجدول والشبكة البيانية، مما يسهل الفهم والتمثيل العملي للاقتربات. تشمل الوثيقة أيضًا تطبيقات وبعض الأمثلة العملية على كل اقتران لتعزيز الفهم.

1. التمثيل البياني للاقترانات المثلثية الرياضيات الصف العاشر وزارة التربية والتعليم فلسطين

2. التمثيل البياني للاقترانات المثلثية اقتران الجيب اقتران جيب التمام اقتران الظـــــل

3. التمثيل البياني للاقترانات المثلثية أولاً : اقتران الجيب ارسم منحنى الاقتران ص = جا س الخطوات 1) نكون الجدول التالي : 0 ﺐ 2 ﺐ 1 -1 0.5 - 0.5 2) نكون الشبكة البيانية ونحدد عليها النقاط ، ثم نصل بين النقاط . التالي س 0 لئب /4 لب /2 3 ﺐ /4 لب 5 بب /4 3 ﺐ /2 7 ﺐ /4 2 ﺐ ص 0 0.7 1 0.7 0 -0.7 -1 -0.7 0 ﺐ 4 ﺐ 2 3 ﺐ 4 5 ﺐ 4 3 ﺐ 2 7 ﺐ 4

4. خصائص اقتران الجيب 1 ) بما أن الزوايا المتكافئة لها نفس النسب المثلثية المناظرة فإن منحنى الاقتران ص = جا س يكرر نفسه في فترات متساوية طول كل منها 2 ﺐ ومثل هذه الاقترانات تسمى اقترانات دورية ، ومقدار دورة هذا الاقتران = 2 ﺐ . 2) القيمة العظمى لهذا الاقتران = 1 ، والقيمة الصغرى = -1 وسعة هذا الاقتران = القيمة العظمى – القيمة الصغري 2 = 1 – ( -1) = 1 2 3) مجال هذا الاقتران = ح ، ومداه هو -1  ص  1 4) منحنى الاقتران متماثل حول نقطة الأصل فهو اقتران فردي

5. مثال : ارسم منحنى الاقتران ص = 2 جا س نكون الجدول التالي : 0 ﺐ 2 ﺐ 1 -1 0.5 - 0.5 2 1.5 - 1.5 -2 التالي س 0 لئب /4 لب /2 3 ﺐ /4 لب 5 بب /4 3 ﺐ /2 7 ﺐ /4 2 ﺐ ص 0 1.4 2 1.4 0 -1.4 -2 -1.4 0 ﺐ 4 ﺐ 2 3 ﺐ 4 5 ﺐ 4 3 ﺐ 2 7 ﺐ 4

6. ارسم منحنيات الاقترانات التالية : 1) ص = جا 2 س 2) ص = 2 جا ( س ) +1 3) ص = جا س 4) ص = جا س رجوع إلى القائمة الرئيسية 1 2 1 2

7. ثانياً : اقتران جيب التمام الخطوات 1) نكون الجدول التالي : ارسم منحنى الاقتران ص = جتا س 0 ﺐ 2 ﺐ 1 -1 0.5 - 0.5 2) نكون الشبكة البيانية ونحدد عليها النقاط ، ثم نصل بين النقاط . التالي س 0 لئب /4 لب /2 3 ﺐ /4 لب 5 بب /4 3 ﺐ /2 7 ﺐ /4 2 ﺐ ص 1 0.7 0 -0.7 -1 -0.7 0 0.7 1 ﺐ 4 ﺐ 2 3 ﺐ 4 5 ﺐ 4 3 ﺐ 2 7 ﺐ 4

8. خصائص اقتران جيب التمام 1 ) الاقتران دوري ومقدار دورته 2 ﺐ . 2) القيمة العظمى لهذا الاقتران = 1 ، والقيمة الصغرى = -1. 3) سعة الاقتران = 1 4) مجال الاقتران = ح ، ومداه : -1  ص  1 5) منحنى الاقتران ص = جتا س هو نفس منحنى الاقتران ص = جاس بانسحاب قدره  /2 إلى اليسار 6) منحنى الاقتران ص = جتا س متماثل حول محور الصادات فهو اقتران زوجي ، جتا س = جتا ( - س ) 7) منحنى الاقتران ص = جتا س هو نفس منحنى الاقتران ص = جتا ( - س ) . التالي

9. مثال : ارسم منحنى الاقتران ص = جتا ( س ) + 1 0 ﺐ 2 ﺐ 1 -1 0.5 - 0.5 2 1.5 التالي س 0 لئب /4 لب /2 3 ﺐ /4 لب 5 بب /4 3 ﺐ /2 7 ﺐ /4 2 ﺐ ص 2 1.7 1 0.3 0 0.3 1 1.7 2 ﺐ 4 ﺐ 2 3 ﺐ 4 5 ﺐ 4 3 ﺐ 2 7 ﺐ 4

10. ارسم منحنيات الاقترانات التالية : 1) ص = جتا 2 س 2) ص = 2 جتا ( س ) +1 3) ص = جتا س 4) ص = جتا س رجوع إلى القائمة الرئيسية 1 2 1 2

11. ثانياً : اقتران الظل الخطوات 1) نكون الجدول التالي : ارسم منحنى الاقتران ص = ظا س 2) نكون الشبكة البيانية ونحدد عليها النقاط ، ثم نصل بين النقاط . 0 ﺐ 2 ﺐ 1 -1 0.5 - 0.5 2 1.5 التالي س 0 لئب /4 لب /2 3 ﺐ /4 لب 5 بب /4 3 ﺐ /2 7 ﺐ /4 2 ﺐ ص 0 1 غير معرف -1 0 1 غير معرف -1 0 ﺐ 4 ﺐ 2 3 ﺐ 4 5 ﺐ 4 3 ﺐ 2 7 ﺐ 4 س 0 لئب /4 لب /2 3 ﺐ /4 لب 5 بب /4 3 ﺐ /2 7 ﺐ /4 2 ﺐ ص 0 1 غير معرف -1 0 1 غير معرف -1 0

12. خصائص اقتران الظل 1 ) الاقتران دوري ومقدار دورته  . 2) مجال الاقتران = ح ــ {  /2 + ن  ، ن تنتمي لـ ص } 3) الاقتران غير معرف عند {  /2 + ن  ، ن تنتمي لـ ص } ويسمى الخط الرأسي عند أي قيمة من هذه القيم خطاً تقاربياً ، لأن منحنى الاقتران يقترب منه ولكن لا يقطعه . 4) مدى الاقتران هو ح 5) منحنى الاقتران ص = ظاا س متماثل حول نقطة الأصل فهو افتران فردي . التالي التالي

13. ارسم منحنيات الاقترانات التالية : 1) ص = ظا ( س )+1 2) ص = 2 ظا ( س ) +1 3) ص = ظا س 4) ص = ظا س رجوع إلى القائمة الرئيسية 1 2 1 2