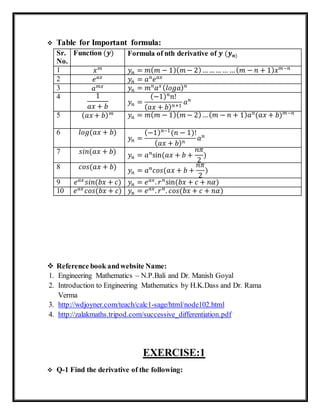
This document discusses successive differentiation and provides examples of finding the nth derivative of common functions such as polynomials, exponentials, logarithms, trigonometric functions, and rational functions. Some key points covered include: - The nth derivative of a function y with respect to x is denoted as d^n y/dx^n. - Standard formulas are given for finding the nth derivative of functions such as x^m, e^ax, a^x, 1/(ax+b), (ax+b)^m, log(ax+b), sin(ax+b), and cos(ax+b). - Examples demonstrate calculating specific high-order derivatives such as the 10th derivative of x

1. Course: B.Sc CS.
Subject: Discrete Mathematics
Unit-1
RAI UNIVERSITY, AHMEDABAD

2. Unit-1 Successive Differentiation
 Review of Differentiation:
 The limit of incremental ratio. i.e. lim⁡
𝛿𝑦
𝛿𝑥
as ⁡𝛿𝑥 approaches zero is
called differential coefficient of 𝑦 with respect of 𝑥 and denoted by
𝑑𝑦
𝑑𝑥
.

𝑑𝑦
𝑑𝑥
=⁡ lim
𝛿𝑥→0
𝛿𝑦
𝛿𝑥

𝑑
𝑑𝑥
𝑓( 𝑥) = lim
𝛿𝑥→0
𝑓( 𝑥+⁡𝛿𝑥)−𝑓(𝑥)
⁡𝛿𝑥
 Standard Results:
 Successive Differentiation:
 If 𝑦 = 𝑓( 𝑥), its differential co-efficient
𝑑𝑦
𝑑𝑥
is also a function of 𝑥.
𝑑𝑦
𝑑𝑥
is
further differentiated and the derivative of
𝑑𝑦
𝑑𝑥
i.e.
𝑑
𝑑𝑥
(
𝑑𝑦
𝑑𝑥
) is called the
second differential co-efficient of 𝑦 and is denoted by
𝑑2 𝑦
𝑑𝑥2
.

3. Similarly third differential coefficient of 𝑦 with respect to 𝑥 is written
as
𝑑3 𝑦
𝑑𝑥3
.
 Other notations of successivederivatives are
𝐷𝑦, 𝐷2
𝑦, 𝐷3
𝑦,………. . 𝐷 𝑛
𝑦 …… ……
𝑦1,⁡⁡⁡𝑦2,⁡⁡⁡⁡𝑦3, ………..⁡⁡𝑦𝑛⁡ ……………..
𝑦′
, 𝑦′′
,⁡𝑦′′′
,……… 𝑦 𝑛
…………….
Thus
𝑑 𝑛 𝑦
𝑑𝑥 𝑛
is 𝑛𝑡ℎ⁡derivative of 𝑦 with respectto 𝑥.
 Example-1. Find the value of
𝒅 𝟑 𝒚
𝒅𝒙 𝟑
if 𝒚 = 𝐥𝐨𝐠⁡( 𝒂𝒙 + 𝒃)
Solution: Here we have 𝑦 = log⁡( 𝑎𝑥 + 𝑏)

𝑑𝑦
𝑑𝑥
=
𝑎
𝑎𝑥+𝑏
 Differentiating it again, we get

𝑑2 𝑦
𝑑𝑥2
=
−𝑎2
( 𝑎𝑥+𝑏)2
 Similarly, ⁡
𝑑3 𝑦
𝑑𝑥3
=
2𝑎3
( 𝑎𝑥+𝑏)3
 𝒏𝒕𝒉 Derivative of 𝒙 𝒎
:
 Let 𝑦 = 𝑥 𝑚
 𝑦1 = 𝑚𝑥 𝑚−1
 𝑦2 = 𝑚( 𝑚 − 1) 𝑥 𝑚−2
 𝑦3 = 𝑚( 𝑚 − 1)( 𝑚 − 2) 𝑥 𝑚−3
 ………………………………………………………..
 …………………………………………………………
 𝑦𝑛 = [ 𝑚( 𝑚 − 1)( 𝑚 − 2)… …up⁡to⁡n⁡factors]⁡× 𝑥 𝑚−𝑛
 𝒚 𝒏 = 𝒎( 𝒎− 𝟏)( 𝒎 − 𝟐) ……………( 𝒎 − 𝒏 + 𝟏) 𝒙 𝒎−𝒏
where 𝒎 <
𝑛
 Example-1. Find the 𝟏𝟎𝒕𝒉 derivative of 𝒙 𝟏𝟐
.
Solution: let 𝑦 = 𝑥12
 𝑦10 = 12 × 11 × 10× ………× 3 × 𝑥2
Note : If m be Positive integer and if 𝑚 = 𝑛 then
𝑑 𝑚
𝑑𝑥 𝑚
𝑥 𝑚
= 𝑚!
 𝒏𝒕𝒉⁡Derivative of 𝒆 𝒂𝒙
:
 𝑦 = 𝑒 𝑎𝑥

4.  𝑦1 = 𝑎𝑒 𝑎𝑥
 𝑦2 = 𝑎2
𝑒 𝑎𝑥
 𝑦3 = 𝑎3
𝑒 𝑎𝑥
 ………………………………………..
 ………………………………………..
 𝒚 𝒏 = 𝒂 𝒏
𝒆 𝒂𝒙
 Example-1. Find the 𝟓𝒕𝒉 derivative of⁡𝒆 𝒎𝒙
.
Solution: Let 𝑦 = 𝑒 𝑚𝑥
∴ 𝑦5 = 𝑚5
𝑒 𝑚𝑥
 𝒏𝒕𝒉⁡Derivative of 𝒂 𝒎𝒙
:
 Let 𝑦 = 𝑎 𝑚𝑥
 𝑦1 = 𝑚𝑎 𝑚𝑥
𝑙𝑜𝑔𝑎⁡
 𝑦2 = 𝑚2
𝑎 𝑚𝑥( 𝑙𝑜𝑔𝑎)2
 ……………………………………….
 ……………………………………….
By generalization,
 𝒚 𝒏 = 𝒎 𝒏
𝒂 𝒙(𝒍𝒐𝒈𝒂) 𝒏
Note: If 𝑚 = 1 i.e. 𝑦 = 𝑎 𝑥
then 𝑦𝑛 = 𝑎 𝑥( 𝑙𝑜𝑔𝑎) 𝑛
 Example-1. Find the 7th
derivative of 𝟐 𝟏𝟎𝒙
.
Solution: Let 𝑦 = 210𝑥
 We know that 𝑦𝑛 = 𝑚 𝑛
𝑎 𝑥( 𝑙𝑜𝑔𝑎) 𝑛
………………………(1)
 Putting 𝑎 = 2, 𝑚 = 10⁡&⁡𝑛 = 7 in (1) we get
 𝑦7⁡ = (10)7(2)10𝑥( 𝑙𝑜𝑔2)7
 𝒏𝒕𝒉⁡derivative of
𝟏
(𝒂𝒙+𝒃)
:
 Let 𝑦 =
𝟏
(𝒂𝒙+𝒃)
 𝑦1 =
−1
( 𝑎𝑥+𝑏)2
. 𝑎
 𝑦2 =
(−1)(−2)
( 𝑎𝑥+𝑏)3
𝑎2
 𝑦3 =
(−1)(−2)(−3)
( 𝑎𝑥+𝑏)4
𝑎3
=
(−1)33!
( 𝑎𝑥+𝑏)4
𝑎3

5.  ……………………………………………………
 ……………………………………………………
 Similarly 𝒚 𝒏 =
(−𝟏) 𝒏 𝒏!
( 𝒂𝒙+𝒃) 𝒏+𝟏
𝒂 𝒏
 Example-1. Find the 30th
derivative of
𝟏
(𝟐𝒙+𝟑)
.
Solution∶ Let ⁡𝑦 =
1
(2𝑥+3)
 𝑦30 =
(−1)30⁡30!
(2𝑥+3)31
230
 𝑦30 =
30!
(2𝑥+3)31
230
 𝒏𝒕𝒉⁡ Derivative of ( 𝒂𝒙 + 𝒃) 𝒎
:
 Let 𝑦 = ( 𝑎𝑥 + 𝑏) 𝑚
 𝑦1 = 𝑚𝑎(𝑎𝑥 + 𝑏) 𝑚−1
 𝑦2 = 𝑚( 𝑚 − 1) 𝑎2
(𝑎𝑥 + 𝑏) 𝑚−2
 𝑦3 = 𝑚( 𝑚 − 1)( 𝑚 − 2) 𝑎3
(𝑎𝑥 + 𝑏) 𝑚−3
 …………………………………………………………..
 …………………………………………………………..
 𝒚 𝒏 = 𝒎( 𝒎− 𝟏)( 𝒎 − 𝟐) ………( 𝒎 − 𝒏 + 𝟏) 𝒂 𝒏
(𝒂𝒙 + 𝒃) 𝒎−𝒏
 Example-1. Find the 10th
derivative of ( 𝟑𝒙 + 𝟒) 𝟏𝟓
.
Solution: Let 𝑦 = (3𝑥 + 4)15
 𝑦10 = 15(15− 1)(15 − 2)…… ……(15− 10 + 1)310(3𝑥 + 4)15−10
 𝑦10 = (15)(14)(13)(12)……………(6)310(3𝑥 + 4)5
 𝒏𝒕𝒉⁡derivative of 𝐥𝐨𝐠⁡( 𝒂𝒙 + 𝒃):
 Let 𝑦 = log⁡( 𝑎𝑥 + 𝑏)
 𝑦1 =
𝑎
𝑎𝑥+𝑏
 Differentiating again, we get
 𝑦2 =
(−1)
( 𝑎𝑥+𝑏)2
𝑎2

6.  𝑦3 =
(−1)(−2)
( 𝑎𝑥+𝑏)3
𝑎3
 𝑦4 =
(−1)(−2)(−3)
( 𝑎𝑥+𝑏)4
𝑎4
 ………………………………………………………………….
 ………………………………………………………………….
 𝑦𝑛 =
(−1)(−2)(−3)…(−𝑛+1)
( 𝑎𝑥+𝑏) 𝑛
𝑎 𝑛
 𝑦𝑛 =
(−1) 𝑛−11.2.3….(𝑛−1)
( 𝑎𝑥+𝑏) 𝑛
𝑎 𝑛
 𝒚 𝒏 =
(−𝟏) 𝒏−𝟏(𝒏−𝟏)!
( 𝒂𝒙+𝒃) 𝒏
𝒂 𝒏
 Example: 1. Find the 9th
derivative of⁡⁡𝒍𝒐𝒈(𝟓𝒙 + 𝟕).
Solution: Let 𝑦 = log(5𝑥 + 7)
 𝑦9 =
(−1)9−1(9−1)!
(5𝑥+7)9
59
 𝑦9 =
8!⁡59
(5𝑥+7)9
 𝒏𝒕𝒉 derivative of 𝐬𝐢𝐧( 𝒂𝒙 + 𝒃):
 Let 𝑦 = 𝑠𝑖𝑛(𝑎𝑥 + 𝑏)
 𝑦1 = ⁡𝑎𝑐𝑜𝑠(𝑎𝑥 + 𝑏) = 𝑎𝑠𝑖𝑛⁡( 𝑎𝑥 + 𝑏 +
𝜋
2
)
 𝑦2 = 𝑎2
cos (𝑎𝑥 + 𝑏 +
𝜋
2
) = 𝑎2
sin⁡( 𝑎𝑥 + 𝑏 +
2𝜋
2
)
 ………………………………………………………………………….
.
 ………………………………………………………………………….
.
 𝒚 𝒏 = 𝒂 𝒏
𝐬𝐢𝐧⁡( 𝒂𝒙 + 𝒃 +
𝒏𝝅
𝟐
)
 Similarly 𝒏𝒕𝒉 derivative of 𝒄𝒐𝒔( 𝒂𝒙 + 𝒃):
 𝒚 𝒏 = 𝒂 𝒏
𝒄𝒐𝒔(𝒂𝒙 + 𝒃 +
𝒏𝝅
𝟐
)
 Example-1. If⁡𝒚 = 𝒔𝒊𝒏𝟐𝒙𝒔𝒊𝒏𝟑𝒙, find⁡𝒚 𝒏.
 Here, we have 𝑦 = 𝑠𝑖𝑛2𝑥. 𝑠𝑖𝑛3𝑥
 𝑦 =
1
2
[2𝑠𝑖𝑛3𝑥𝑠𝑖𝑛2𝑥]

7.  𝑦 =
1
2
[𝑐𝑜𝑠𝑥 − 𝑐𝑜𝑠5𝑥]
 Differentiating 𝑛 times, we get
 𝑦𝑛 =
1
2
[
𝑑 𝑛
𝑑𝑥 𝑛
𝑐𝑜𝑠𝑥 −
𝑑 𝑛
𝑑𝑥 𝑛
𝑐𝑜𝑠5𝑥]
 𝑦𝑛 =
1
2
[𝑐𝑜𝑠(𝑥 +
𝑛𝜋
2
) − 5 𝑛
𝑐𝑜𝑠(5𝑥 +
𝑛𝜋
2
)]
 Example-2. If 𝒚 = 𝐬𝐢𝐧 𝟐
𝒙 𝐜𝐨𝐬 𝟑
𝒙 find⁡𝒚 𝒏.
Solution: Here we have
 𝑦 = 𝑠𝑖𝑛2
𝑥. 𝑐𝑜𝑠3
𝑥
 𝑦 = 𝑠𝑖𝑛2
𝑥. 𝑐𝑜𝑠2
𝑥. 𝑐𝑜𝑠𝑥⁡ (2𝑠𝑖𝑛𝑥. 𝑐𝑜𝑠𝑥 = 𝑠𝑖𝑛2𝑥)
 𝑦 =
1
4
( 𝑠𝑖𝑛2𝑥)2
𝑐𝑜𝑠𝑥 (sin2
2𝑥 =
1−𝑐𝑜𝑠4𝑥
2
)
 𝑦 =
1
8
(2 𝑠𝑖𝑛2
2𝑥)𝑐𝑜𝑠𝑥
 𝑦 =
1
8
(1 − 𝑐𝑜𝑠4𝑥) 𝑐𝑜𝑠𝑥
 𝑦 =
1
8
(𝑐𝑜𝑠𝑥 − 𝑐𝑜𝑠4𝑥. 𝑐𝑜𝑠𝑥)
 𝑦 =
1
8
( 𝑐𝑜𝑠𝑥) −
1
16
(2𝑐𝑜𝑠4𝑥. 𝑐𝑜𝑠𝑥)
 𝑦 =
1
8
𝑐𝑜𝑠𝑥 −
1
16
[𝑐𝑜𝑠5𝑥 + 𝑐𝑜𝑠3𝑥] ⁡⁡⁡⁡⁡⁡[∵ 2𝑐𝑜𝑠𝐴𝑐𝑜𝑠𝐵 = cos( 𝐴 + 𝐵) +
⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡cos( 𝐴 − 𝐵)]
 Now Differentiating n times w.r.t. 𝑥 we get
 𝑦𝑛 =
1
8
cos (𝑥 +
𝑛𝜋
2
) −
1
16
5 𝑛
cos (5𝑥 +
𝑛𝜋
2
) −
1
16
. 3 𝑛
cos⁡(3𝑥 +
𝑛𝜋
2
)
 𝒏𝒕𝒉⁡derivative of 𝒆 𝒂𝒙
𝐬𝐢𝐧⁡( 𝒃𝒙 + 𝒄):
 Let 𝑦 = 𝑒 𝑎𝑥
𝑆𝑖𝑛(𝑏𝑥 + 𝑐)
 𝑦1 = 𝑎𝑒 𝑎𝑥
. sin( 𝑏𝑥 + 𝑐) + 𝑒 𝑎𝑥
. 𝑏cos( 𝑏𝑥 + 𝑐)
 𝑦1 = 𝑒 𝑎𝑥
[𝑎sin( 𝑏𝑥 + 𝑐) + 𝑏cos( 𝑏𝑥 + 𝑐)]
 𝑦1 = 𝑒 𝑎𝑥
[𝑟𝑐𝑜𝑠𝛼sin( 𝑏𝑥 + 𝑐) + 𝑟𝑠𝑖𝑛𝛼cos⁡( 𝑏𝑥 + 𝑐)]
 𝑦1 = 𝑒 𝑎𝑥
𝑟 sin( 𝑏𝑥 + 𝑐 + 𝛼)
 Similarly 𝑦2 = 𝑒 𝑎𝑥
𝑟2
sin( 𝑏𝑥 + 𝑐 + 2𝛼)

8.  …………………………………………………………………………………..
 …………………………………………………………………………………..
 𝑦𝑛 = 𝑒 𝑎𝑥
. 𝑟 𝑛
sin⁡( 𝑏𝑥 + 𝑐 + 𝑛𝛼)
Where 𝑟2
= 𝑎2
+ 𝑏2
and 𝑡𝑎𝑛𝛼 =
𝑏
𝑎
 Similarly if 𝒚 = 𝒆 𝒂𝒙
𝒄𝒐𝒔(𝒃𝒙 + 𝒄)
 𝒚 𝒏 = 𝒆 𝒂𝒙
. 𝒓 𝒏
. 𝒄𝒐𝒔(𝒃𝒙 + 𝒄 + 𝒏𝜶)
 Example: 1. Find the 𝒏𝒕𝒉 derivative of 𝒆 𝒙
. 𝐬𝐢𝐧 𝟑
𝒙
Solution: we have, 𝑦 = 𝑒 𝑥
sin3
𝑥
 We know that ,
 𝑠𝑖𝑛3𝑥 = 3𝑠𝑖𝑛𝑥 − 4sin3
𝑥
 ∴ 𝑆𝑖𝑛3
𝑥 =
1
4
[3𝑠𝑖𝑛𝑥 − 𝑠𝑖𝑛3𝑥]
 Let 𝑦 = 𝑒 𝑥
sin3
𝑥
 𝑦 = 𝑒 𝑥
.
1
4
[3𝑠𝑖𝑛𝑥 − 𝑠𝑖𝑛3𝑥]
 𝑦 =
3
4
𝑒 𝑥
𝑠𝑖𝑛𝑥 −
1
4
𝑒 𝑥
𝑠𝑖𝑛3𝑥
 Differentiating n times, we get
 𝑦𝑛 =
3
4
(12
+ 12)
𝑛
2. 𝑒 𝑥
sin (𝑥 + 𝑛𝑡𝑎𝑛−1 1
1
) −
1
4
(12
+ 32)
𝑛
2. 𝑒 𝑥
sin⁡[3𝑥 +
𝑛𝑡𝑎𝑛−1 3
1
]
 𝑦𝑛 =
3
4
2
𝑛
2 𝑒 𝑥
sin (𝑥 +
𝑛𝜋
4
) −
1
4
. 10
𝑛
2. 𝑒 𝑥
sin⁡(3𝑥 + 𝑛𝑡𝑎𝑛−1
3)
 Example: 2. Find the 𝒏𝒕𝒉 derivative of 𝒆 𝒂𝒙
. 𝒄𝒐𝒔 𝟐
𝒙. 𝒔𝒊𝒏𝒙
 𝑦 = 𝑒 𝑎𝑥
. 𝑐𝑜𝑠2
𝑥. 𝑠𝑖𝑛𝑥⁡
 𝑦 =
1
2
𝑒 𝑎𝑥 ( 𝑐𝑜𝑠2𝑥 + 1) 𝑠𝑖𝑛𝑥 (cos2
𝑥 =
1+𝑐𝑜𝑠2𝑥
2
)
 𝑦 =
1
2
𝑒 𝑎𝑥
. 𝑐𝑜𝑠2𝑥. 𝑠𝑖𝑛𝑥 +
1
2
𝑒 𝑎𝑥
𝑠𝑖𝑛𝑥
 𝑦 =
1
4
𝑒 𝑎𝑥 ( 𝑠𝑖𝑛3𝑥 − 𝑠𝑖𝑛𝑥) +
1
2
𝑒 𝑎𝑥
𝑠𝑖𝑛𝑥

9. {2𝑐𝑜𝑠𝐴𝑠𝑖𝑛𝐵 = 𝑆𝑖𝑛( 𝐴 + 𝐵) − 𝑆𝑖𝑛( 𝐴 − 𝐵)}
 𝑦 =
1
4
𝑒 𝑎𝑥
𝑠𝑖𝑛3𝑥 −
1
4
𝑒 𝑎𝑥
𝑠𝑖𝑛𝑥 +
1
2
𝑒 𝑎𝑥
𝑠𝑖𝑛𝑥
 𝑦 =
1
4
𝑒 𝑎𝑥
𝑠𝑖𝑛3𝑥 +
1
4
𝑒 𝑎𝑥
𝑠𝑖𝑛𝑥
 We know that
𝑑 𝑛
𝑑𝑥 𝑛
( 𝑒 𝑎𝑥
. 𝑠𝑖𝑛𝑏𝑥) = 𝑒 𝑎𝑥
. (𝑎2
+ 𝑏2
)
𝑛
2.sin⁡( 𝑏𝑥 +
𝑛 tan−1 𝑏
𝑎
)
 Thus,𝑦𝑛 =
1
4
( 𝑎2
+ 32)
𝑛
2 𝑒 𝑎𝑥
.sin⁡(3𝑥 + 𝑛 tan−1 3
𝑎
) +
1
4
( 𝑎2
+ 12)
𝑛
2 𝑒 𝑎𝑥
.
sin⁡( 𝑥 + 𝑛𝑡𝑎𝑛−1 1
𝑎
).
𝒏𝒕𝒉 derivative of function by using Partial Fraction:
 Example-1. If 𝒚 =
𝟏
𝟏−𝟓𝒙+𝟔𝒙 𝟐
⁡find 𝒚 𝒏.
Solution: Here, we have 𝑦 =
1
1−5𝑥+6𝑥2
 ∴ 𝑦 =
1
(2𝑥−1)(3𝑥−1)
 ∴
1
(2𝑥−1)(3𝑥−1)
=
𝐴
2𝑥−1
+
𝐵
3𝑥−1
 ∴ 1 = 𝐴(3𝑥 − 1) + 𝐵(2𝑥 − 1) -----------------------------------------(1)
 To find A and B
 we put first 𝑥 =
1
3
in equation (1) we get 𝐵 = −3
 we put 𝑥 =
1
2
in equation (1) we get 𝐴 = 2
 ∴
1
(2𝑥−1)(3𝑥−1)
=
2
2𝑥−1
−
3
3𝑥−1
 Differentiating n times ,we get 𝑦𝑛 = 2𝐷 𝑛
(
1
2𝑥−1
) − 3𝐷 𝑛
(
1
3𝑥−1
)
 𝑦𝑛 = 2[
(−1) 𝑛.𝑛!(2) 𝑛
(2𝑥−1) 𝑛+1
] − 3[
(−1) 𝑛 𝑛!(3) 𝑛
(3𝑥−1) 𝑛+1
]
 𝑦𝑛 = (−1) 𝑛
. 𝑛! [
2 𝑛+1
(2𝑥−1) 𝑛+1
−
3 𝑛+1
(3𝑥−1) 𝑛+1
]

10.  Example-2. If 𝒚 = 𝒙𝒍𝒐𝒈
𝒙−𝟏
𝒙+𝟏
, show that 𝒚 𝒏 = (−𝟏) 𝒏−𝟐( 𝒏 − 𝟐)![
𝒙−𝒏
( 𝒙−𝟏) 𝒏
−
𝒙+𝒏
( 𝒙+𝟏) 𝒏
]
Solution: Here, we have ⁡𝑦 = 𝑥𝑙𝑜𝑔
𝑥−1
𝑥+1
 𝑦 = 𝑥 [log( 𝑥 − 1) − log(𝑥 + 1)]
 Differentiating with respectto 𝑥 we get
 𝑦1 = 𝑥 (
1
𝑥−1
−
1
𝑥+1
) + log( 𝑥 − 1) − log( 𝑥 + 1)
 𝑦1 = (
𝑥
𝑥−1
−
𝑥
𝑥+1
) + log( 𝑥 − 1) − log( 𝑥 + 1)
 𝑦1 = 1 +
1
𝑥−1
− 1 +
1
𝑥+1
+ log( 𝑥 − 1) − log( 𝑥 + 1)
 𝑦1 =
1
𝑥−1
+
1
𝑥+1
+ log( 𝑥 − 1) − log( 𝑥 + 1)
 Again Differentiating ,(n-1) times with respectto ′𝑥′, we get
 𝑦𝑛 =
(−1) 𝑛−1(𝑛−1)!
( 𝑥−1) 𝑛
+
(−1) 𝑛−1(𝑛−1)!
( 𝑥+1) 𝑛
+
(−1) 𝑛−2(𝑛−2)!
( 𝑥−1) 𝑛−1
−
(−1) 𝑛−2(𝑛−2)!
( 𝑥+1) 𝑛−1
 𝑦𝑛 = (−1) 𝑛−2( 𝑛 − 2)![
(−1)( 𝑛−1)
( 𝑥−1) 𝑛
+
(−1)( 𝑛−1)
( 𝑥+1) 𝑛
+
𝑥−1
( 𝑥−1) 𝑛
−
𝑥+1
( 𝑥+1) 𝑛
]
 𝑦𝑛 = (−1) 𝑛−2( 𝑛 − 2)![
𝑥−𝑛
( 𝑥−1) 𝑛
−
𝑥+𝑛
( 𝑥+1) 𝑛
]

11.  Table for Important formula:
Sr.
No.
Function (𝒚) Formula of nth derivative of 𝒚 (𝒚 𝒏)
1 𝑥 𝑚
𝑦𝑛 = 𝑚( 𝑚 − 1)( 𝑚 − 2)………… …( 𝑚 − 𝑛 + 1) 𝑥 𝑚−𝑛
2 𝑒 𝑎𝑥
𝑦𝑛 = 𝑎 𝑛
𝑒 𝑎𝑥
3 𝑎 𝑚𝑥 𝑦𝑛 = 𝑚 𝑛
𝑎 𝑥 ( 𝑙𝑜𝑔𝑎) 𝑛
4 1
𝑎𝑥 + 𝑏
𝑦𝑛 =
(−1) 𝑛
𝑛!
( 𝑎𝑥 + 𝑏) 𝑛+1
𝑎 𝑛
5 ( 𝑎𝑥 + 𝑏) 𝑚 𝑦𝑛 = 𝑚( 𝑚 − 1)( 𝑚 − 2)…( 𝑚 − 𝑛 + 1) 𝑎 𝑛
(𝑎𝑥 + 𝑏) 𝑚−𝑛
6 𝑙𝑜𝑔(𝑎𝑥 + 𝑏)
𝑦𝑛 =
(−1) 𝑛−1
(𝑛 − 1)!
( 𝑎𝑥 + 𝑏) 𝑛
𝑎 𝑛
7 𝑠𝑖𝑛(𝑎𝑥 + 𝑏) 𝑦𝑛 = 𝑎 𝑛
sin⁡( 𝑎𝑥 + 𝑏 +
𝑛𝜋
2
)
8 𝑐𝑜𝑠(𝑎𝑥 + 𝑏) 𝑦𝑛 = 𝑎 𝑛
𝑐𝑜𝑠(𝑎𝑥 + 𝑏 +
𝑛𝜋
2
)
9 𝑒 𝑎𝑥
𝑠𝑖𝑛(𝑏𝑥 + 𝑐) 𝑦𝑛 = 𝑒 𝑎𝑥
. 𝑟 𝑛
sin⁡( 𝑏𝑥 + 𝑐 + 𝑛𝛼)
10 𝑒 𝑎𝑥
𝑐𝑜𝑠(𝑏𝑥 + 𝑐) 𝑦𝑛 = 𝑒 𝑎𝑥
. 𝑟 𝑛
. 𝑐𝑜𝑠(𝑏𝑥 + 𝑐 + 𝑛𝛼)
 Reference book andwebsite Name:
1. Engineering Mathematics – N.P.Bali and Dr. Manish Goyal
2. Introduction to Engineering Mathematics by H.K.Dass and Dr. Rama
Verma
3. http://wdjoyner.com/teach/calc1-sage/html/node102.html
4. http://zalakmaths.tripod.com/successive_differentiation.pdf
EXERCISE:1
 Q-1 Find the derivative of the following:

12. 1. Obtain 5th ⁡derivative of 𝑒2𝑥
2. Obtain 3rd derivative of 35𝑥
3. Obtain 4th derivative of (2𝑥 + 3)5
4. Obtain 4th derivative of
1
2𝑥+3
 Q-2 Find the nth derivative of the following:
1. cos2
𝑥
2. 𝑠𝑖𝑛2𝑥𝑐𝑜𝑠3𝑥
3. 𝑒 𝑥
𝑠𝑖𝑛4𝑥𝑐𝑜𝑠6𝑥⁡
4. 𝑒2𝑥
𝑐𝑜𝑠𝑥𝑠𝑖𝑛2
2𝑥
5. 𝑐𝑜𝑠𝑥𝑐𝑜𝑠2𝑥𝑐𝑜𝑠3𝑥
 Q-3 Find the nth derivative of the following by using partial fraction:
1.
1
( 𝑥−1)2(𝑥−2)
2.
1
𝑎2−𝑥2
3.
𝑥4
( 𝑥−1)(𝑥−2)
4.
𝑥
( 𝑥−𝑎)(𝑥−𝑏)
5.
𝑥+1
𝑥2−4