This document discusses the rules of differentiation, including:
1. The chain rule for finding derivatives of composite functions. Examples are provided to demonstrate applying the chain rule.
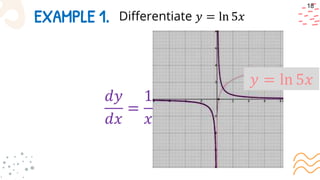
2. Derivatives of exponential and logarithmic functions. The formulas and rules for taking derivatives of exponential, natural logarithm, and general logarithmic functions are provided. Examples demonstrate applying these rules.
3. Derivatives of trigonometric functions. The formulas and rules for taking derivatives of sine, cosine, tangent, cotangent, secant, and cosecant functions are stated. Examples demonstrate applying these rules to find derivatives of trigonometric functions.