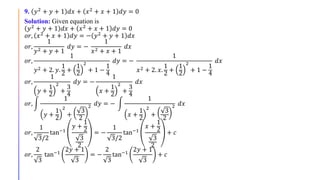The document discusses the solution of first-order and first-degree differential equations using the variable separation method. It details how to separate variables, integrate both sides, and includes various example equations with step-by-step solutions. Additionally, it emphasizes the importance of the arbitrary constant in solving differential equations.

1. SOLUTION OF
FIRST ORDER AND FIRST DEGREE
DIFFERENTIAL EQUATIONS
Variable separation method
Md. Aminul Islam

2. A differential equation of first order and first degree is an equation of the form
𝑑𝑦
𝑑𝑥
= 𝑓 𝑥, 𝑦 , 𝑜𝑟 𝑀 𝑑𝑥 + 𝑁 𝑑𝑦 = 0
If in an equation, it is possible to get all the functions of x and dx to one side, and all
the functions of 𝑦 and 𝑑𝑦 to the other, the variables are said to be separable.
Variables separable
First order and first degree differential equations

3. Rule to solve an equation in which the variables are separable
Consider the equation
𝑑𝑦
𝑑𝑥
= 𝑋𝑌 , where 𝑋 is a function of 𝑥 and 𝑌 is a function of 𝑦 only.
 Given equation is
𝑑𝑦
𝑑𝑥
= 𝑋𝑌

1
𝑌
𝑑𝑦 = 𝑋 𝑑𝑥, that is, variables have been separated
 Integrating both sides,
1
𝑌
𝑑𝑦 = 𝑋 𝑑𝑥 + 𝑐, where c is the arbitrary constant, is the
required solution.
Note:
 Never forget to add an arbitrary constant on one side only. A solution without this
constant is wrong, for it is not the general solution.
 The nature of the arbitrary constant depends upon on the nature of the problem.
 The solution of a differential equation must be put in a form as simple as possible.

4. 1. 𝑥 𝑦2
+ 𝑥 𝑑𝑥 + 𝑦 𝑥2
+ 𝑦 𝑑𝑦 = 0
2. 𝑒 𝑦
+ 1 cos 𝑥 𝑑𝑥 + 𝑒 𝑦
sin 𝑥 𝑑𝑦 = 0
3. 𝑠𝑒𝑐2 𝑥 tan 𝑦 𝑑𝑥 + 𝑠𝑒𝑐2 𝑦 tan 𝑥 𝑑𝑦 = 0
4. 𝑥2
y + 1 dx + 𝑦2
𝑥 − 1 𝑑𝑦 = 0
5. 3 𝑒 𝑥
tan 𝑦 𝑑𝑥 + 1 − 𝑒 𝑥
𝑠𝑒𝑐2
𝑦 𝑑𝑦 = 0
6. 𝑒2𝑥−3𝑦
𝑑𝑥 + 𝑒2𝑦−3𝑥
𝑑𝑦 = 0
7.
𝑑𝑦
𝑑𝑥
= 𝑒 𝑥+𝑦 + 𝑥2 𝑒 𝑥3+𝑦
8. 𝑥 1 − 𝑦2 𝑑𝑥 + 𝑦 1 − 𝑥2 𝑑𝑦 = 0
9. 𝑦2
+ 𝑦 + 1 𝑑𝑥 + 𝑥2
+ 𝑥 + 1 𝑑𝑦 = 0
10.
𝑑𝑦
𝑑𝑥
=
𝑥 (2 log 𝑥+1)
sin 𝑦+𝑦 cos 𝑦
Solve the following differential equations

5. 11. 1 − 𝑥2 𝑑𝑦 + 𝑥𝑦 𝑑𝑥 = 𝑥𝑦2 𝑑𝑥
12. 𝑥 cos 𝑦 𝑑𝑦 = 𝑒 𝑥
𝑥 log 𝑥 + 1 𝑑𝑥
13. 1 + 𝑥 1 + 𝑦2
𝑑𝑥 + 1 + 𝑦 1 + 𝑥2
𝑑𝑦 = 0
14. If
𝑑𝑦
𝑑𝑥
= 𝑒 𝑥+𝑦 and it is given that for 𝑥 = 1, 𝑦 = 1, find y when 𝑥 = −1.
15.Find the particular solution of the differential equation log
𝑑𝑦
𝑑𝑥
= 3𝑥 + 4𝑦 given that
𝑦 = 0 when 𝑥 = 0
16. Find the equation of the curve represented by 𝑦 − 𝑦𝑥 𝑑𝑥 + 𝑥 + 𝑥𝑦 𝑑𝑦 = 0 and
passing through the point 1,1 .
17. Find the equation of the curve that passes through the point (1,2) and has at every
point
𝑑𝑦
𝑑𝑥
= −
2𝑥𝑦
𝑥2+1
Solve the following differential equations

6. 1. 𝑥 𝑦2
+ 𝑥 𝑑𝑥 + 𝑦 𝑥2
+ 𝑦 𝑑𝑦 = 0
Solution: Given equation is
𝑥 𝑦2 + 𝑥 𝑑𝑥 + 𝑦 𝑥2 + 𝑦 𝑑𝑦 = 0
𝑜𝑟, 𝑦 𝑥2 + 𝑦 𝑑𝑦 = − 𝑥 𝑦2 + 𝑥 𝑑𝑥
𝑜𝑟, 𝑦 𝑥2 + 1 𝑑𝑦 = −𝑥 𝑦2 + 1 𝑑𝑥
𝑜𝑟,
𝑦
𝑦2 + 1
𝑑𝑦 = −
𝑥
𝑥2 + 1
𝑑𝑥
𝑜𝑟,
2𝑦
𝑦2 + 1
𝑑𝑦 = −
2𝑥
𝑥2 + 1
𝑑𝑥
𝑜𝑟, ln 𝑦2 + 1 = − ln 𝑥2 + 1 + ln 𝑐
𝑜𝑟, ln 𝑦2
+ 1 + ln 𝑥2
+ 1 = ln 𝑐
𝑜𝑟, ln[ 𝑦2 + 1 𝑥2 + 1 ] = ln 𝑐
𝑜𝑟, 𝑦2 + 1 𝑥2 + 1 = 𝑐
Which is the required solution.
𝑓′
(𝑥)
𝑓(𝑥)
𝑑𝑥 = ln 𝑓 𝑥 + 𝑐

7. 2. 𝑒 𝑦
+ 1 cos 𝑥 𝑑𝑥 + 𝑒 𝑦
sin 𝑥 𝑑𝑦 = 0
Solution: Given equation is
𝑒 𝑦
+ 1 cos 𝑥 𝑑𝑥 + 𝑒 𝑦
sin 𝑥 𝑑𝑦 = 0
𝑜𝑟, 𝑒 𝑦 sin 𝑥 𝑑𝑦 = − 𝑒 𝑦 + 1 cos 𝑥 𝑑𝑥
𝑜𝑟,
𝑒 𝑦
𝑒 𝑦 + 1
𝑑𝑦 = −
cos 𝑥
sin 𝑥
𝑑𝑥
𝑜𝑟,
𝑒 𝑦
𝑒 𝑦 + 1
𝑑𝑦 = −
cos 𝑥
sin 𝑥
𝑑𝑥
𝑜𝑟, ln 𝑒 𝑦 + 1 = − ln sin 𝑥 + ln 𝑐
𝑜𝑟, ln 𝑒 𝑦 + 1 + ln sin 𝑥 = ln 𝑐
𝑜𝑟, ln[ 𝑒 𝑦
+ 1 sin 𝑥 ] = ln 𝑐
𝑜𝑟, 𝑒 𝑦 + 1 sin 𝑥 = 𝑐
which is the required solution.
3. 𝑠𝑒𝑐2 𝑥 tan 𝑦 𝑑𝑥 + 𝑠𝑒𝑐2 𝑦 tan 𝑥 𝑑𝑦 = 0
Solution: Given equation is
𝑠𝑒𝑐2 𝑥 tan 𝑦 𝑑𝑥 + 𝑠𝑒𝑐2 𝑦 tan 𝑥 𝑑𝑦 = 0
𝑜𝑟, 𝑠𝑒𝑐2 𝑦 tan 𝑥 𝑑𝑦 = −𝑠𝑒𝑐2 𝑥 tan 𝑦 𝑑𝑥
𝑜𝑟,
𝑠𝑒𝑐2 𝑦
tan 𝑦
𝑑𝑦 = −
𝑠𝑒𝑐2 𝑥
tan 𝑥
𝑑𝑥
𝑜𝑟,
𝑠𝑒𝑐2
𝑦
tan 𝑦
𝑑𝑦 = −
𝑠𝑒𝑐2
𝑥
tan 𝑥
𝑑𝑥
𝑜𝑟, ln tan 𝑦 = − ln tan 𝑥 + ln 𝑐
𝑜𝑟, ln tan 𝑦 + ln tan 𝑥 = ln 𝑐
𝑜𝑟, ln tan 𝑦 tan 𝑥 = ln 𝑐
𝑜𝑟, tan 𝑦 tan 𝑥 = c
which is the required solution.

8. 𝟒. 𝑥2
y + 1 dx + 𝑦2
𝑥 − 1 𝑑𝑦 = 0
Solution: Given equation is 𝑥2 y + 1 dx + 𝑦2 𝑥 − 1 𝑑𝑦 = 0
𝑜𝑟, 𝑦2 𝑥 − 1 𝑑𝑦 = −𝑥2 y + 1 dx
𝑜𝑟,
𝑦2
𝑦 + 1
𝑑𝑦 = −
𝑥2
𝑥 − 1
𝑑𝑥 𝑜𝑟,
𝑦2 − 1 + 1
𝑦 + 1
𝑑𝑦 = −
𝑥2 − 1 + 1
𝑥 − 1
𝑑𝑥
𝑜𝑟,
(𝑦 + 1)(𝑦 − 1) + 1
𝑦 + 1
𝑑𝑦 = −
𝑥 + 1 𝑥 − 1 + 1
𝑥 − 1
𝑑𝑥
𝑜𝑟,
(𝑦 + 1)(𝑦 − 1)
𝑦 + 1
+
1
𝑦 + 1
𝑑𝑦 = −
𝑥 + 1 𝑥 − 1
𝑥 − 1
+
1
𝑥 − 1
𝑑𝑥
𝑜𝑟, 𝑦 − 1 +
1
𝑦 + 1
𝑑𝑦 = − 𝑥 + 1 +
1
𝑥 − 1
𝑑𝑥
𝑜𝑟,
𝑦2
2
− 𝑦 + ln 𝑦 + 1 = −
𝑥2
2
+ 𝑥 + ln 𝑥 − 1 + 𝑐
Which is the required solution.

9. 5. 3 𝑒 𝑥
tan 𝑦 𝑑𝑥 + 1 − 𝑒 𝑥
𝑠𝑒𝑐2
𝑦 𝑑𝑦 = 0
Solution: Given equation is
3 𝑒 𝑥 tan 𝑦 𝑑𝑥 + 1 − 𝑒 𝑥 𝑠𝑒𝑐2 𝑦 𝑑𝑦 = 0
𝑜𝑟, 1 − 𝑒 𝑥 𝑠𝑒𝑐2 𝑦 𝑑𝑦 = −3 𝑒 𝑥 tan 𝑦 𝑑𝑥
𝑜𝑟,
𝑠𝑒𝑐2 𝑦
tan 𝑦
𝑑𝑦 = −3
𝑒 𝑥
1 − 𝑒 𝑥
𝑑𝑥
𝑜𝑟,
𝑠𝑒𝑐2 𝑦
tan 𝑦
𝑑𝑦 = 3
𝑒 𝑥
𝑒 𝑥 − 1
𝑑𝑥
𝑜𝑟, ln tan 𝑦 = 3 ln 𝑒 𝑥 − 1 + 𝑐
which is the required solution
6. 𝑒2𝑥−3𝑦
𝑑𝑥 + 𝑒2𝑦−3𝑥
𝑑𝑦 = 0
Solution: Given equation is
𝑒2𝑥−3𝑦 𝑑𝑥 + 𝑒2𝑦−3𝑥 𝑑𝑦 = 0
𝑜𝑟, 𝑒2𝑦−3𝑥 𝑑𝑦 = −𝑒2𝑥−3𝑦 𝑑𝑥
𝑜𝑟,
𝑒2𝑦
𝑒3𝑥
𝑑𝑦 = −
𝑒2𝑥
𝑒3𝑦
𝑑𝑥
𝑜𝑟, 𝑒2𝑦 . 𝑒3𝑦 𝑑𝑦 = −𝑒2𝑥 . 𝑒3𝑥 𝑑𝑥
𝑜𝑟, 𝑒5𝑦
𝑑𝑦 = − 𝑒5𝑥
𝑑𝑥
𝑜𝑟,
𝑒5𝑦
5
= −
𝑒5𝑥
5
+
𝑐
5
𝑜𝑟, 𝑒5𝑦
= −𝑒5𝑥
+ 𝑐
which is the required solution
𝑒 𝑚𝑥
𝑑𝑥 =
𝑒 𝑚𝑥
𝑚
+ 𝑐
𝑎 𝑚−𝑛 =
𝑎 𝑚
𝑎 𝑛

10. 7.
𝑑𝑦
𝑑𝑥
= 𝑒 𝑥+𝑦
+ 𝑥2
𝑒 𝑥3+𝑦
Solution: Given equation is
𝑑𝑦
𝑑𝑥
= 𝑒 𝑥+𝑦
+ 𝑥2
𝑒 𝑥3+𝑦
= 𝑒 𝑥
𝑒 𝑦
+ 𝑥2
𝑒 𝑥3
𝑒 𝑦
𝑜𝑟, 𝑑𝑦 = 𝑒 𝑦 𝑒 𝑥 + 𝑥2 𝑒 𝑥3
𝑑𝑥
𝑜𝑟,
1
𝑒 𝑦
𝑑𝑦 = 𝑒 𝑥 𝑑𝑥 + 𝑥2 𝑒 𝑥3
𝑑𝑥
𝑜𝑟, 𝑒−𝑦 𝑑𝑦 = 𝑒 𝑥 𝑑𝑥 + 𝑒 𝑥3
𝑥2 𝑑𝑥
𝑜𝑟, −𝑒−𝑦 = 𝑒 𝑥 +
1
3
𝑒 𝑧 𝑑𝑧
𝑜𝑟, −𝑒−𝑦 = 𝑒 𝑥 +
1
3
𝑒 𝑧 + 𝑐
𝑜𝑟, −𝑒−𝑦
= 𝑒 𝑥
+
1
3
𝑒 𝑥3
+ 𝑐
8. 𝑥 1 − 𝑦2 𝑑𝑥 + 𝑦 1 − 𝑥2 𝑑𝑦 = 0
Solution: Given equation is
𝑥 1 − 𝑦2 𝑑𝑥 + 𝑦 1 − 𝑥2 𝑑𝑦 = 0
𝑜𝑟, 𝑦 1 − 𝑥2 𝑑𝑦 = −𝑥 1 − 𝑦2 𝑑𝑥
𝑜𝑟,
𝑦
1 − 𝑦2
𝑑𝑦 = −
𝑥
1 − 𝑥2
𝑑𝑥
𝑜𝑟, −
−2𝑦
1 − 𝑦2
𝑑𝑦 =
−2𝑥
1 − 𝑥2
𝑑𝑥
𝑜𝑟, −2 1 − 𝑦2 = 2 1 − 𝑥2 + 𝑐
𝑓′
(𝑥)
𝑓(𝑥)
𝑑𝑥 = 2 𝑓 𝑥 + 𝑐
Let 𝑥3
= 𝑧
Then 3𝑥2 𝑑𝑥 = 𝑑𝑧
𝑜𝑟, 𝑥2
𝑑𝑥 =
1
3
𝑑𝑧

11. 9. 𝑦2 + 𝑦 + 1 𝑑𝑥 + 𝑥2 + 𝑥 + 1 𝑑𝑦 = 0
Solution: Given equation is
𝑦2 + 𝑦 + 1 𝑑𝑥 + 𝑥2 + 𝑥 + 1 𝑑𝑦 = 0
𝑜𝑟, 𝑥2 + 𝑥 + 1 𝑑𝑦 = − 𝑦2 + 𝑦 + 1 𝑑𝑥
𝑜𝑟,
1
𝑦2 + 𝑦 + 1
𝑑𝑦 = −
1
𝑥2 + 𝑥 + 1
𝑑𝑥
𝑜𝑟,
1
𝑦2 + 2. 𝑦.
1
2
+
1
2
2
+ 1 −
1
4
𝑑𝑦 = −
1
𝑥2 + 2. 𝑥.
1
2
+
1
2
2
+ 1 −
1
4
𝑑𝑥
𝑜𝑟,
1
𝑦 +
1
2
2
+
3
4
𝑑𝑦 = −
1
𝑥 +
1
2
2
+
3
4
𝑑𝑥
𝑜𝑟,
1
𝑦 +
1
2
2
+
3
2
2 𝑑𝑦 = −
1
𝑥 +
1
2
2
+
3
2
2 𝑑𝑥
𝑜𝑟,
1
3/2
tan−1
𝑦 +
1
2
3
2
= −
1
3/2
tan−1
𝑥 +
1
2
3
2
+ 𝑐
𝑜𝑟,
2
3
tan−1
2𝑦 + 1
3
= −
2
3
tan−1
2𝑦 + 1
3
+ 𝑐

12. 𝟏𝟎.
𝑑𝑦
𝑑𝑥
=
𝑥 (2 log 𝑥 + 1)
sin 𝑦 + 𝑦 cos 𝑦
Solution: Given equation is
𝑑𝑦
𝑑𝑥
=
𝑥 (2 log 𝑥 + 1)
sin 𝑦 + 𝑦 cos 𝑦
𝑜𝑟, sin 𝑦 𝑑𝑦 + 𝑦 cos 𝑦 𝑑𝑦 = 2 𝑥 log 𝑥 𝑑𝑥 + 𝑥 𝑑𝑥
𝑜𝑟, sin 𝑦 𝑑𝑦 + 𝑦 cos 𝑦 𝑑𝑦 = 2 𝑥 log 𝑥 𝑑𝑥 + 𝑥 𝑑𝑥
𝑜𝑟, − cos 𝑦 + 𝑦 cos 𝑦 𝑑𝑦 −
𝑑
𝑑𝑦
𝑦 cos 𝑦 𝑑𝑦 𝑑𝑦
= 2 log 𝑥 𝑥 𝑑𝑥 − 2
𝑑
𝑑𝑥
log 𝑥 𝑥 𝑑𝑥 𝑑𝑥 +
𝑥2
2
𝑜𝑟, − cos 𝑦 + 𝑦 sin 𝑦 − sin 𝑦 𝑑𝑦 = 2 log 𝑥.
𝑥2
2
− 2
1
𝑥
.
𝑥2
2
𝑑𝑥 +
𝑥2
2
𝑜𝑟, − cos 𝑦 + 𝑦 sin 𝑦 + cos 𝑦 = 𝑥2
log 𝑥 − 𝑥 𝑑𝑥 +
𝑥2
2
𝑜𝑟, − cos 𝑦 + 𝑦 sin 𝑦 + cos 𝑦 = 𝑥2 log 𝑥 −
𝑥2
2
+
𝑥2
2
+ 𝑐
𝑜𝑟, − cos 𝑦 + 𝑦 sin 𝑦 + cos 𝑦 = 𝑥2 log 𝑥 + 𝑐

13. 11. 1 − 𝑥2 𝑑𝑦 + 𝑥𝑦 𝑑𝑥 = 𝑥𝑦2 𝑑𝑥
Solution: Given equation is
1 − 𝑥2
𝑑𝑦 + 𝑥𝑦 𝑑𝑥 = 𝑥𝑦2
𝑑𝑥
𝒐𝒓, 1 − 𝑥2
𝑑𝑦 = 𝑥𝑦2
𝑑𝑥 − 𝑥𝑦 𝑑𝑥
𝒐𝒓, 1 − 𝑥2 𝑑𝑦 = 𝑥 𝑦(𝑦 − 1) 𝑑𝑥
𝑜𝑟,
1
𝑦 (𝑦 − 1)
𝑑𝑦 =
𝑥
1 − 𝑥2
𝑑𝑥
𝑜𝑟,
𝑦 − (𝑦 − 1)
𝑦 (𝑦 − 1)
𝑑𝑦 = −
𝑥
𝑥2 − 1
𝑑𝑥
𝑜𝑟,
1
𝑦 − 1
−
1
𝑦
𝑦 = −
1
2
2𝑥
𝑥2 − 1
𝑑𝑥
𝑜𝑟, ln 𝑦 − 1 − ln 𝑦 = −
1
2
ln 𝑥2 − 1 + 𝑐
which is the required solution
12. 𝑥 cos 𝑦 𝑑𝑦 = 𝑒 𝑥 𝑥 log 𝑥 + 1 𝑑𝑥
Solution: Given equation is
𝑥 cos 𝑦 𝑑𝑦 = 𝑒 𝑥 𝑥 log 𝑥 + 1 𝑑𝑥
𝑜𝑟, cos 𝑦 𝑑𝑦 = log 𝑥 𝑒 𝑥 𝑑𝑥 +
1
𝑥
𝑒 𝑥 𝑑𝑥
𝑜𝑟, cos 𝑦 𝑑𝑦 = log 𝑥 𝑒 𝑥
𝑑𝑥
+
1
𝑥
𝑒 𝑥
𝑑𝑥 + 𝑐
𝑜𝑟, sin 𝑦 = log 𝑥 𝑒 𝑥
−
1
𝑥
𝑒 𝑥
𝑑𝑥
1
𝑥
𝑒 𝑥
𝑑𝑥 + 𝑐
𝑜𝑟, sin 𝑦 = log 𝑥 𝑒 𝑥
+ 𝑐
which is the required solution

14. 13. 1 + 𝑥 1 + 𝑦2 𝑑𝑥 + 1 + 𝑦 1 + 𝑥2 𝑑𝑦 = 0
Solution: Given equation is
1 + 𝑥 1 + 𝑦2 𝑑𝑥 + 1 + 𝑦 1 + 𝑥2 𝑑𝑦 = 0
𝑜𝑟, 1 + 𝑦 1 + 𝑥2 𝑑𝑦 = − 1 + 𝑥 1 + 𝑦2 𝑑𝑥
𝑜𝑟,
1 + 𝑦
1 + 𝑦2
𝑑𝑦 = −
1 + 𝑥
1 + 𝑥2
𝑑𝑥
𝑜𝑟,
1
1 + 𝑦2
+
1
2
2𝑦
1 + 𝑦2
𝑑𝑦 = −
1
1 + 𝑥2
+
1
2
2𝑥
1 + 𝑥2
𝑑𝑥
𝑜𝑟, tan−1 𝑦 +
1
2
ln 1 + 𝑦2 = − tan−1 𝑥 −
1
2
ln 1 + 𝑥2 + 𝑐
which is the required solution

15. 14. If
𝑑𝑦
𝑑𝑥
= 𝑒 𝑥+𝑦
and it is given that for
𝑥 = 1, 𝑦 = 1, find y when 𝑥 = −1.
Solution: we have
𝑑𝑦
𝑑𝑥
= 𝑒 𝑥+𝑦 = 𝑒 𝑥 𝑒 𝑦 𝑜𝑟, 𝑒−𝑦 𝑑𝑦 = 𝑒 𝑥 𝑑𝑥
𝑜𝑟, 𝑒−𝑦
𝑑𝑦 = 𝑒 𝑥
𝑑𝑥
𝑜𝑟, −𝑒−𝑦 = 𝑒 𝑥 + 𝑐 … … (𝑖)
given that for 𝑥 = 1, 𝑦 = 1, then (𝑖) becomes
−𝑒−1
= 𝑒1
+ 𝑐
𝑜𝑟, 𝑐 = −𝑒 −
1
𝑒
= −
𝑒2 + 1
𝑒
From i , we get − 𝑒−𝑦
= 𝑒 𝑥
−
𝑒2 + 1
𝑒
when 𝑥 = −1, −𝑒−𝑦 =
1
𝑒
−
𝑒2
+ 1
𝑒
= −
𝑒2
𝑒
𝑜𝑟, −𝑒−𝑦 = −𝑒1
𝑜𝑟, 𝑒−𝑦 = 𝑒1
𝑜𝑟, −𝑦 = 1
Therefore, 𝑦 = −1
15. Find the particular solution of the
differential equation log
𝑑𝑦
𝑑𝑥
= 3𝑥 + 4𝑦 given
that 𝑦 = 0 when 𝑥 = 0
Solution: Given equation is
log
𝑑𝑦
𝑑𝑥
= 3𝑥 + 4𝑦
𝑜𝑟,
𝑑𝑦
𝑑𝑥
= 𝑒3𝑥+4𝑦
= 𝑒3𝑥
𝑒4𝑦
𝑜𝑟, 𝑒−4𝑦 𝑑𝑦 = 𝑒3𝑥 𝑑𝑥
𝑜𝑟, 𝑒−4𝑦
𝑑𝑦 = 𝑒3𝑥
𝑑𝑥
𝑜𝑟,
𝑒−4𝑦
−4
=
𝑒3𝑥
3
+ 𝑐
given that 𝑦 = 0 when 𝑥 = 0.
then we get
1
−4
=
1
3
+ 𝑐 𝑜𝑟, 𝑐 = −
7
12
Then the required particular solution is
𝑒−4𝑦
−4
=
𝑒3𝑥
3
−
7
12

16. 16. Find the equation of the curve represented by 𝑦 − 𝑦𝑥 𝑑𝑥 + 𝑥 + 𝑥𝑦 𝑑𝑦 = 0
and passing through the point 1,1 .
Solution: Given equation is 𝑦 − 𝑦𝑥 𝑑𝑥 + 𝑥 + 𝑥𝑦 𝑑𝑦 = 0
𝑜𝑟, 𝑥 1 + 𝑦 𝑑𝑦 = −𝑦 1 − 𝑥 𝑑𝑥
𝑜𝑟,
1 + 𝑦
𝑦
𝑑𝑦 = −
1 − 𝑥
𝑥
𝑑𝑥
𝑜𝑟,
1
𝑦
+ 1 𝑑𝑦 = −
1
𝑥
− 1 𝑑𝑥
𝑜𝑟,
1
𝑦
+ 1 𝑑𝑦 = −
1
𝑥
− 1 𝑑𝑥
𝑜𝑟, ln 𝑦 + 𝑦 = − ln 𝑥 − 𝑥 + 𝑐 … … (𝑖)
Since the curve 𝑖 passing through the point 1,1 , we get
ln 1 + 1 = − ln 1 − 1 + 𝑐 𝑜𝑟, 𝑐 = 0
Putting 𝑐 = 0 in 𝑖 , we get
ln 𝑦 + 𝑦 = − ln 𝑥 − 𝑥 𝑜𝑟, ln 𝑦 + ln 𝑥 + 𝑦 − 𝑥 = 0
𝑜𝑟, ln 𝑥𝑦 + 𝑦 − 𝑥 = 0 which is the required equation of the curve

17. 17. Find the equation of the curve that passes through the point (1,2) and has at
every point
𝑑𝑦
𝑑𝑥
= −
2𝑥𝑦
𝑥2+1
Solution: Given equation is
𝑑𝑦
𝑑𝑥
= −
2𝑥𝑦
𝑥2+1
𝑜𝑟,
1
𝑦
𝑑𝑦 = −
2𝑥
𝑥2 + 1
𝑑𝑥
𝑜𝑟,
1
𝑦
𝑑𝑦 = −
2𝑥
𝑥2 + 1
𝑑𝑥
𝑜𝑟, ln 𝑦 = − ln 𝑥2 + 1 + ln 𝑐
𝑜𝑟, ln 𝑦 + ln 𝑥2
+ 1 = ln 𝑐
𝑜𝑟, ln 𝑦 𝑥2
+ 1 = ln 𝑐
𝑜𝑟, 𝑦 𝑥2 + 1 = 𝑐 … … (𝑖)
Since the curve 𝑖 passing through the point 1,2 , we get
2 12 + 1 = 𝑐
𝑜𝑟, 𝑐 = 4
Putting 𝑐 = 4 in 𝑖 , we get
𝑦 𝑥2 + 1 = 4 which is the required equation of the curve

18.  Bali, N.P., 2006. Golden Differential Equations. Firewall Media.
References