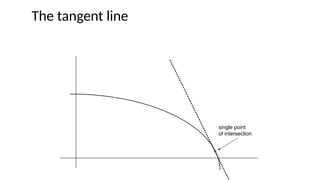
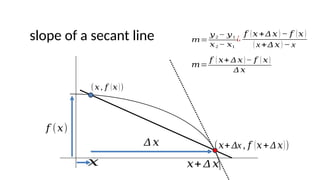
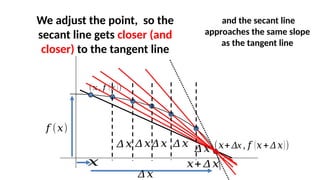
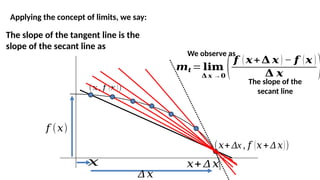
The document outlines the learning outcomes for students regarding the concept of derivatives in calculus, emphasizing the ability to derive differentiation rules and apply them to real-life situations. It provides detailed explanations and examples of various differentiation rules such as the power rule, product rule, and quotient rule, along with practical applications in business and population growth metrics. Additionally, it encourages learners to connect mathematical concepts to their personal values and experiences.

1. Derivative of a Function

2. Learning Outcomes
At the end of the session, the learners shall be able
to
• derive the differentiation rules,
• apply the differentiation rules in computing the derivative of
algebraic functions,
• relate the concept of differentiation rules to real-life
situations, and
• Connect the concept of derivatives to learner’s life values,
motto in life and as a Senior High School learner.

3. The tangent line
single point
of intersection

4. slope of a secant line
𝑥+ Δ 𝑥
𝑥
𝑓 (𝑥)
(𝑥+ Δx , 𝑓 (𝑥+ Δ 𝑥))
(𝑥, 𝑓 (𝑥))
Δ 𝑥
𝑚=
𝑦2 − 𝑦1
𝑥2 − 𝑥1
¿
𝑓 (𝑥+Δ 𝑥 ) − 𝑓 (𝑥)
( x+Δ 𝑥) − x
𝑚=
𝑓 ( 𝑥+ Δ 𝑥 )− 𝑓 ( 𝑥)
Δ 𝑥

5. We adjust the point, so the
secant line gets closer (and
closer) to the tangent line
𝑥+ Δ 𝑥
𝑥
𝑓 (𝑥)
(𝑥+ Δx , 𝑓 (𝑥+ Δ 𝑥))
(𝑥, 𝑓 (𝑥))
Δ 𝑥
and the secant line
approaches the same slope
as the tangent line
Δ 𝑥 Δ 𝑥Δ 𝑥 Δ 𝑥 Δ 𝑥

6. 𝑥+ Δ 𝑥
𝑥
𝑓 (𝑥)
(𝑥+ Δx , 𝑓 (𝑥+ Δ 𝑥))
(𝑥, 𝑓 (𝑥))
Δ 𝑥
Applying the concept of limits, we say:
The slope of the tangent line is the
slope of the secant line as
𝒎𝒕 = 𝐥𝐢𝐦
𝚫 𝒙 →𝟎
(𝒇 ( 𝒙+𝚫 𝒙 ) − 𝒇 (𝒙 )
𝚫 𝒙 )
The slope of the
secant line
We observe as

7. The First Principle
of Derivative
What is a Derivative?
•It measures how a function changes at a certain point.
•the slope of the line tangent to the curve
•The process of solving the derivative is differentiation.
•It is applied to study the changes in businesses,
economics, motion, astronomy, etc.
𝑦
′
= 𝑓
′
( 𝑥 )=
𝑑𝑦
𝑑𝑥
=𝑚= lim
Δ 𝑥→ 0
(𝑓 ( 𝑥 +Δ 𝑥 ) − 𝑓 (𝑥 )
Δ 𝑥 )

8. Example 1
Find the derivative of
Since , it follows that
𝑑𝑦
𝑑𝑥
= lim
∆ 𝑥→ 0
(𝑓 (𝑥+∆ 𝑥)− 𝑓 (𝑥)
∆ 𝑥 )
¿ lim
∆ 𝑥→0
((𝑥+ Δ𝑥)2
−𝑥
2
∆𝑥 )

9. Example 1
𝑑𝑦
𝑑𝑥
= lim
∆ 𝑥→ 0
(𝑓 (𝑥+∆ 𝑥)− 𝑓 (𝑥)
∆ 𝑥 )
¿ lim
∆ 𝑥→0
((𝑥+ Δ𝑥)2
−𝑥
2
∆𝑥 )
¿ lim
∆ 𝑥 → 0
𝑥
2
+2𝑥 ( Δ 𝑥 )+( Δ 𝑥)2
− 𝑥
2
∆ 𝑥
¿ lim
∆ 𝑥 → 0
2 𝑥( Δ 𝑥)+( Δ 𝑥)2
∆ 𝑥
¿ lim
∆ 𝑥 → 0
Δ 𝑥(2 𝑥+ Δx)
∆ 𝑥

10. Example 1
¿ lim
∆ 𝑥 → 0
𝑥2
+2𝑥 ( Δ 𝑥 )+( Δ 𝑥)2
− 𝑥2
∆ 𝑥
¿ lim
∆ 𝑥 → 0
2 𝑥( Δ 𝑥)+( Δ 𝑥)2
∆ 𝑥
¿ lim
∆ 𝑥 → 0
Δ 𝑥(2 𝑥+ Δx)
∆ 𝑥
¿ lim
∆ 𝑥 → 0
(2 𝑥+ Δx)
¿2 𝑥+0
𝒅𝒚
𝒅𝒙
=2 𝒙

12. BASIC DIFFERENTIATION
RULES
Since the process of the First Principle of Derivatives is lengthy,
we will explore the different rules to efficiently find the
derivatives of functions.

13. Differentiation
Rules
Thm. 1: Constant Rule
If any constant and for all , then,
or or
Examples:
Find the derivative of the functions:
𝑑𝑦
𝑑𝑥
=0
𝑓 ′
(𝑥 )=0
𝑦 ′=0

14. Differentiation
Rules
Thm. 2: Power Rule
If is a power function for some real number , then
Example 1:
Find the derivative of the function:
𝑦 =𝑥4
𝑑
𝑑𝑥
(𝑥4
)=4 𝑥3
𝑦 ′=4 𝑥3

15. Differentiation
Rules
Example 2:
Find the derivative of the function:
𝑔(𝑥)=
3
√𝑥
4
Laws of Exponents
Power Rule
Laws of Exponents

16. Differentiation
Rules
Example 3:
Find the derivative of the function:
𝑦 =
1
𝑥
5
Laws of Exponents
Power Rule
Laws of Exponents
𝑑𝑦
𝑑𝑥
=−
5
𝑥
6
𝑑
𝑑𝑥 ( 1
𝑥
5 )=−
5
𝑥
6

17. Differentiation
Rules
Thm. 3: Trigonometric Differentiation
Thm 3.a:
Thm 3.b:
Thm 3.c:
Thm 3.d:
Thm 3.e:
Thm 3.f:

18. Differentiation
Rules
Thm. 4: Constant Multiple Rule
If is a constant and is a differentiable function, then,
Example 1:
Find the derivative of the function:
𝑦 =− 3 𝑥3

19. Differentiation
Rules
Thm. 4: Constant Multiple Rule
If is a constant and is a differentiable function, then,
Example 2:
Find the derivative of the function:
h (𝑥)=
4
𝑥
3

20. Differentiation
Rules
Thm. 4: Constant Multiple Rule
If is a constant and is a differentiable function, then,
Example 3:
Find the derivative of the function:
𝑦 =−
1
2
csc 𝑥
Thm 3.f

21. Differentiation
Rules
Thm. 5: Sum and Difference Rule
If are differentiable functions, then,
Example 1:
Find the derivative of the function:

22. Differentiation
Rules
Example 2:
Find the derivative of the function:

23. Differentiation
Rules
Example 3:
Find the derivative of the function:

24. Derivative of a Function
(Part 2)

25. Learning Outcomes
At the end of the session, the learners shall be able
to
• derive the differentiation rules,
• apply the differentiation rules in computing the derivative of
algebraic functions,
• relate the concept of differentiation rules to real-life
situations, and
• Connect the concept of derivatives to learner’s life values,
motto in life and as a Senior High School learner.

26. Differentiation
Rules
Thm. 6: Product Rule
If are differentiable functions, then,
Alternative:

27. Thm. 6: Product Rule
If and are differentiable functions in , then,
Example 1:
Find the derivative of the function:
𝑦 =( 𝑥4
− 1 ) ( 𝑥3
−3 𝑥 +2)
Let:
𝑢=𝑥4
− 1 𝑣=𝑥3
−3 𝑥+2
𝑑𝑢=4 𝑥3
𝑑𝑣=3 𝑥2
−3
𝑦 ′=(𝑥4
−1)
(3 𝑥
2
− 3)+¿
(𝑥3
− 3𝑥 +2)
(4 𝑥3
)

28. Thm. 6: Product Rule
If and are differentiable functions in , then,
Example 2:
Find the derivative of the function:
𝑦 = 𝑥 3
cos 𝑥
Let:
𝑢=𝑥3
𝑣=cos 𝑥
𝑑𝑢=3 𝑥2
𝑑𝑣=−sin𝑥
(𝑥3
)
(−sin 𝑥)
+(cos 𝑥)
(3 𝑥2
)
𝑦′
=¿

29. Differentiation
Rules
Thm. 7: Quotient Rule
If are differentiable functions, then,
Alternative:

30. Thm. 7: Quotient Rule
If and are differentiable functions in , then,
Example 1:
Find the derivative of the function:
𝑦 =
2 𝑥 + 5
𝑥
2
+ 1
Let:
𝐻=2𝑥+5 𝐿=𝑥2
+1
𝑑𝐻=2 𝑑𝐿=2 𝑥
(𝑥2
+1)
(2)
𝑦′
=¿ −(2 𝑥+5)
(2 𝑥)
( 𝑥
2
+1)2

31. Thm. 7: Quotient Rule
If and are differentiable functions in , then,
Example 2:
Find the derivative of the function:
𝑦 =
3 sin 𝑥
𝑥
2
+ 4
Let:
𝐻=3sin 𝑥 𝐿=𝑥2
+4
𝑑𝐻=3cos 𝑥𝑑𝐿=2 𝑥
(𝑥2
+4 )
(3 cos 𝑥)
𝑦′
=¿ −(3sin 𝑥)
(2 𝑥)
( 𝑥
2
+4 )2

32. Some Applications of
Differentiation

33. Problem 1
The shipments of digital single-lens reflect cameras (DSLRs)
are projected to be:
, (,
units years from now.
a. How many DSLRs will be shipped after 2 years?
b. What is the rate of DSLR shipments after 2 years?

34. Problem 1
The shipments of digital
single-lens reflect cameras
(SLRs) are projected to be:
, (,
units years from now.
a. How many DSLRs will be
shipped after 2 years?
b. What is the rate of DSLR
shipments after 2 years?
a. Solve for
𝑵 (𝒕)=𝟔𝒕𝟐
+𝟐𝟎𝟎𝒕+𝟐𝟎,𝟎𝟎𝟎
𝑵 (𝟐)=𝟔(𝟐)𝟐
+𝟐𝟎𝟎(𝟐)+𝟐𝟎,𝟎𝟎𝟎
𝑵 (𝟐)=𝟕𝟐+𝟒𝟎𝟎+𝟐𝟎,𝟎𝟎𝟎
𝑵 (𝟐)=𝟐𝟎 , 𝟒𝟕𝟐
There will be units of SLRs
shipments after 2 years.

35. Problem 1
The shipments of digital
single-lens reflect cameras
(DSLRs) are projected to be:
, (,
units years from now.
a. How many DSLRs will be
shipped after 2 years?
b. What is the rate of DSLR
shipments after 2 years?
b. Solve for
𝑵 (𝒕)=𝟔𝒕𝟐
+𝟐𝟎𝟎𝒕+𝟐𝟎,𝟎𝟎𝟎
𝑵′
(𝒕)=𝟐∙𝟔𝒕𝟐 −𝟏
+𝟐𝟎𝟎 𝒕𝟏− 𝟏
The rate of shipment is units of
SLRs per year.
𝑵′
(𝒕)=𝟏𝟐𝒕+𝟐𝟎𝟎
𝑵′
(𝟐)=𝟏𝟐(𝟐)+𝟐𝟎𝟎
𝑵′
(𝟐)=𝟐𝟐 4 per year

36. Problem 2
A construction company is building a mini community of homes,
offices, stores, schools, etc. in a vacant area. The company
estimated that the population in thousands after years is
modeled by the function:
a. What will be the population in the area after 8 years?
b. What is the instantaneous rate of population growth in 8
years?

37. Problem 2
A construction company is building a
mini community of homes, offices,
stores, schools, etc. in a vacant
area. The company estimated that
the population in thousands after
years is modeled by the function:
a. What will be the population in
the area after 8 years?
b. What is the instantaneous rate of
population growth in 8 years?
a. Solve for :
𝑷 (𝟖)=
𝟐𝟓𝟎(𝟖)𝟐
+𝟏𝟎𝟎(𝟖)+𝟓𝟎
𝟑(𝟖)+𝟏𝟓𝟎
𝑷 (𝟖)=
𝟐𝟓𝟎(𝟔𝟒)+𝟏𝟎𝟎(𝟖)+𝟓𝟎
𝟑(𝟖)+𝟏𝟓𝟎
𝑷 (𝟖)=
𝟏𝟔𝟎𝟎𝟎+𝟖𝟎𝟎+𝟓𝟎
𝟐𝟒+𝟏𝟓𝟎
𝑷 (𝟖 )=
𝟏𝟔𝟖𝟓𝟎
𝟏𝟕𝟒
≈ 𝟗𝟔.𝟖𝟑𝟗
The area will approximately
have a population of 96,839
people.

38. Problem 2
A construction company is building a mini community of homes, offices,
stores, schools, etc. in a vacant area. The company estimated that the
population in thousands after years is modelled by the function:
b. What is the instantaneous rate of population growth in 8 years?
Solve for :
𝑷 ′ (𝒕)=
(𝟑𝒕+𝟏𝟓𝟎)(𝟓𝟎𝟎 𝒕+𝟏𝟎𝟎)+(𝟐𝟓𝟎𝒕𝟐
+𝟏𝟎𝟎𝒕+𝟓𝟎)(𝟑)
𝟑(𝟖)+𝟏𝟓𝟎
𝑷 (𝒕 )=
𝟐𝟓𝟎𝒕𝟐
+𝟏𝟎𝟎𝒕 +𝟓𝟎
𝟑𝒕+𝟏𝟓𝟎

39. Problem 2
b. What is the instantaneous rate of population growth in 8 years?
Solve for :
𝑷 ′ (𝒕)=
(𝟑𝒕+𝟏𝟓𝟎)(𝟓𝟎𝟎 𝒕+𝟏𝟎𝟎)+(𝟐𝟓𝟎𝒕𝟐
+𝟏𝟎𝟎𝒕+𝟓𝟎)(𝟑)
(𝟑𝒕+𝟏𝟓𝟎)𝟐
𝑷 ′ (𝒕)=
𝟏𝟓𝟎𝟎 𝒕𝟐
+𝟕𝟓𝟎𝟎𝟎𝒕+𝟑𝟎𝟎𝒕+𝟏𝟓𝟎𝟎𝟎+𝟕𝟓𝟎𝒕𝟐
+𝟑𝟎𝟎𝒕+𝟏𝟓𝟎
(𝟑𝒕+𝟏𝟓𝟎)𝟐
𝑷 ′ (𝒕)=
𝟐𝟐𝟓𝟎 𝒕𝟐
+𝟕𝟓𝟔𝟎𝟎𝒕+𝟏𝟓𝟏𝟓𝟎
(𝟑𝒕 +𝟏𝟓𝟎)𝟐

40. Problem 2
b. What is the instantaneous rate of population growth in 8 years?
Solve for :
𝑷 ′ (𝒕)=
𝟐𝟐𝟓𝟎 𝒕𝟐
+𝟕𝟓𝟔𝟎𝟎𝒕+𝟏𝟓𝟏𝟓𝟎
(𝟑𝒕 +𝟏𝟓𝟎)𝟐
𝑷 ′ (𝟖)=
𝟐𝟐𝟓𝟎(𝟖)𝟐
+𝟕𝟓𝟔𝟎𝟎(𝟖)+𝟏𝟓𝟏𝟓𝟎
(𝟑(𝟖)+𝟏𝟓𝟎)
𝟐 ¿
𝟏𝟒𝟒,𝟎𝟎𝟎+𝟔𝟎𝟒 ,𝟖𝟎𝟎+𝟏𝟓𝟏𝟓𝟎
(𝟐𝟒+𝟏𝟓𝟎)𝟐
𝑷 ′ (𝟖)=
𝟗𝟎𝟑,𝟗𝟓𝟎
𝟑𝟎𝟐.𝟐𝟕𝟔per year
There will be an increase of approximately residents
per year in the area.

41. The concept of derivatives allows us to
measure changes at a given time or
situation.
What are the recent events in your life that
have changed significantly? What are the
representations of these changes?