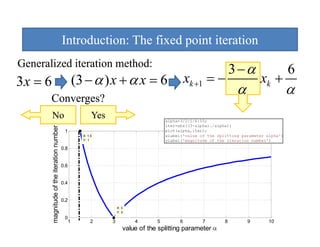
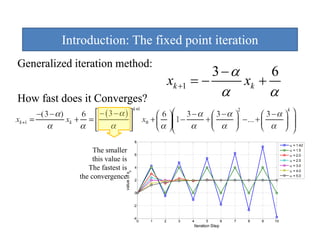
This document discusses iterative methods for solving systems of equations. It introduces the Jacobi iteration method and the Successive Over-Relaxation (SOR) method. SOR can accelerate the convergence compared to Jacobi by introducing an optimal relaxation parameter. Pseudocode is provided to implement SOR to iteratively solve a system of equations until the solution converges within a specified tolerance.

1. Chapter 7.
Iterative Solutions of Systems
of Equations
of Equations
EFLUM – ENAC ‐ EPFL

2. Contents
1.
1 Introduction
2. First example: Scalar Equation
3.
3 Iterative solutions of a system of equations:
i l i f f i
Jacobi iteration method
4. Iterative methods for finite difference
equations: Back to problem 6.3
5. The Successive Over Relaxation (SOR)

3. Introduction: The fixed point iteration
p
Previous Method (used on previous class)
Uses Gaussian Elimination (or “” in MatLab)

4. Introduction: The fixed point iteration
p
The main concept: xk +1 = g ( xk )
Example:
xk
3x = 6 2x + x = 6 xk +1 = − + 3
X0 = 4
4
2
3.5
3
Value of xn
2.5
f
2
1.5
X0 = 1
1
0.5
X0 = 00
0
1 2 3 4 5 6 7 8 9 10
Iteration step

5. Introduction: The fixed point iteration
p
xk
The proof of convergence: xk +1 = − + 3
2
1 2
=
1 + (1 2 ) 3

6. Introduction: The fixed point iteration
p
First Iteration method:
xk
3x = 6 2x + x = 6 xk +1 = − + 3
2
Always Converges
Generalized iteration method:
G li d it ti th d
3 −α 6
3x = 6 (3 − α ) x + α x = 6 xk +1 = − xk +
α α
Converges?

7. Introduction: The fixed point iteration
p
Generalized iteration method:
3 −α 6
3x = 6 (3 − α ) x + α x = 6 xk +1 = − xk +
α α
Converges?
No Yes
mber
1
teration num
X: 1.5
Y:
Y 1
0.8
0.6
magnitu of the it
0.4
ude
0.2
X: 3
Y: 0
0
1 2 3 4 5 6 7 8 9 10
value of the splitting parameter α

8. Introduction: The fixed point iteration
p
Generalized iteration method:
3 −α 6
xk +1 = − xk +
How fast does it Converges?
α α
8
α = 1.42
The smaller α = 1.5
6 α = 2.0
this value is α = 2.5
α = 3.0
The fastest is 4
α =40
4.0
value of xn
the convergence α = 5.0
2
0
-2
-4
0 1 2 3 4 5 6 7 8 9 10
Iteration Step

9. Iterative solution of a system of equations
y q
Jacobi interaction approach
Consider the problem
D: Diagonal elements of A
L: Lower elements of A
+U: Upper elements of A
L+U: Matrix B
and Q <1

10. Iterative solution of a system of equations
y q
Some notes about the vector norm
The vector norm calculation
Some notes about the matrix norm
S t b t th ti
The matrix norm calculation

11. Iterative solution of a system of equations
y q

12. Back to problem 6.3 ( ° case – last class)
p (1°
(1 )
Back to Laplace Equation (Last class example)
M_diag=sparse(1:21,1:21,-4,21,21);
L_diag1=sparse(2:21,1:20,1,21,21);
L_diag2=sparse(8:21,1:14,1,21,21);
L_diag1(8,7)=0; L_diag1(15,14)=0;
A=M_diag+L_diag1+L_diag2+L_diag1'+L_diag2';
A M di +L di 1+L di 2+L di 1'+L di 2'
b=zeros(21,1); b(7)=-100; b(14)=-100; b(21)=-100;
convcrit 1e9;
convcrit=1e9;
iteration matrix is Q=-Dinv*LnU h_old=ones(21,1);
kount=0;
L=L_diag1+L_diag2 while convcrit>1e-3 % loop ends when fractional
U=L‘;
; kount=kount+1; % change in h < 10-3
LnU=L+U; h=Q*h_old+Dinv*b;
convcrit=max(abs(h-h_old)./h);
Dinv=inv(M_diag) %D-1
h_old=h;
end

13. Iterative solution of a system of equations
y q
convcrit=1e9;
h_old=ones(21,1);
kount=0;
while convcrit>1e-3 % loop ends when fractional
kount=kount+1; % change in h < 10-3
h=Q*h_old+Dinv*b;
convcrit=max(abs(h-h_old)./h);
h_old=h;
end

14. Successive over relaxation method
Before Now
Jacobi iteration approach
ρ(Q) = abs(max(eig(Q)))
( ( g(Q)))
Successive Order Relaxation Method
(SOR)
S(ω): Iteration matrix.
ρ(Q): Magnitude of the largest eigenvalue of the
Jacobi iteration matrix.
ωopt: Iteration parameter, chosen to accelerate
convergence

15. Iterative solution of a system of equations
y q
wopt=2/(1+sqrt(1-(normest(Q))^2));
y=inv(D*(1/wopt)+L);
S=-y*(U+(1-(1/wopt))*D);
convcrit=1e9;
it 1 9 it 1 9
convcrit=1e9;
h_old=ones(21,1); h_old=ones(21,1);
kount=0; kount=0;
while convcrit > 1e-3 while convcrit > 1e-3
kount=kount+1; kount=kount+1;
h=Q*h_old+Dinv*b; h=S*h_old+y*b;
convcrit=max(abs(h-h_old)./h); convcrit=max(abs(h-h_old)./h);
h_old=h; h_old=h;
end end
Slow Fast ☺