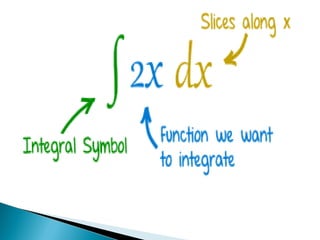
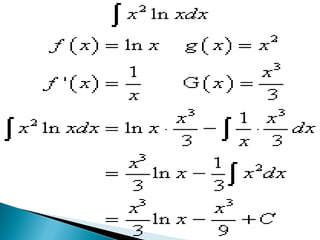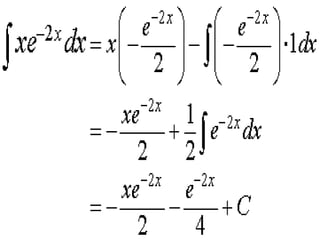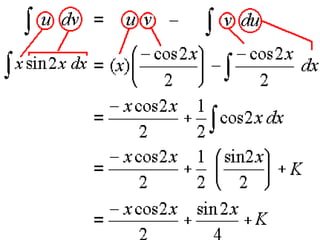The document summarizes key concepts and applications of integration. It discusses: 1) Important historical figures like Archimedes, Gauss, Leibniz and Newton who contributed to the development of integration and calculus. 2) Engineering applications of integration like in the design of the Petronas Towers and Sydney Opera House. 3) The integration by parts formula and examples of using it to evaluate integrals of composite functions.

3. M.Nabeel Khan 61
Daud Mirza 57
Danish Mirza 58
Fawad Usman 66
Amir Mughal 72
M.Arslan 17

7.  -Archimedes is the founder of surface areas and
volumes of solids such as the sphere and the cone.
His integration method was very modern since he did
not have algebra, or the decimal representation of
numbers
 -GAuss was the first to make graphs of integrals.
 -Leibniz and newton discovered calculus and found
that differentiation and integration undo each other
GAuss

9. • -Integration was used to design PETRONAS
Towers making it stronger
• -Many differential equations were used in the
designing of the Sydney Opera House
• was one of the first uses of integration
• -Finding areas under curved surfaces,
• Centers of mass, displacement and
• Velocity, and fluid flow.

11. ( ) '( ) ( ) ( ) ( ) '( )f x g x dx f x g x g x f x dx
udv uv vdu
= −
= −
∫ ∫
∫ ∫
• The idea is to use the above formula to simplify an integration task.
• One wants to find a representation for the function to be integrated
in the form udv so that the function vdu is easier to integrate
than the original function.
• The rule is proved using the Product Rule for differentiation.

12. Example 1:
cosx x dx⋅∫
polynomial factor u x=
u dv uv v du= −∫ ∫
sin cosx x x C⋅ + +
u v v du− ∫
sin sinx x x dx⋅ − ∫

14. Example 2:
ln x dx∫
logarithmic factor
u dv uv v du= −∫ ∫
lnx x x C− +
1
ln x x x dx
x
⋅ − ⋅∫
u v v du− ∫

16. This is still a product, so we
need to use integration by
parts again.
Example 3:
2 x
x e dx∫
2
2x x
x e e x dx− ⋅∫
2
2x x
x e xe dx− ∫
( )2
2x x x
x e xe e dx− − ∫
2
2 2x x x
x e xe e C− + +

19. Example 4(cont.):
cosx
e x dx∫
cosx
e x dx =∫
2 cos sin cosx x x
e x dx e x e x= +∫
sin cos
cos
2
x x
x e x e x
e x dx C
+
= +∫
sin sinx x
e x x e dx− ×∫
sin cos cosx x x
e x e x e x dx+ − ∫
( )sin cos cosx x x
e x e x x e dx− ×− − − ×∫