Computer graphics and machine learning: Smooth differentiable functions are used in optimization algorithms for training models. Conclusion Continuity and differentiability are cornerstones of calculus. Continuity guarantees no sudden jumps in a function, while differentiability provides the slope and rate of change at each point. While all differentiable functions are continuous, not all continuous functions are differentiable, making differentiability the stricter condition. Understanding these concepts is vital, as they not only enrich mathematical theory but also enable practical applications across science, engineering, and economics.

1. CLAVIMATE CLASSES
Continuity and Differentiability
By Shoaib Khan

2. Topics to be covered :-
• Introduction of the topic
• Continuity
• Algebra of a continuous function
• Differentiability
• Derivatives of composite functions
• Derivatives of implicit functions
• Derivatives of inverse trigonometric functions
•Exponential and Logarithmic Functions
•Logarithmic Differentiation
•Derivatives of Functions in Parametric Forms
•Second-Order Derivative
•Mean Value Theorem
• Some Competitive Questions like jee Main based on these Topics

3. Definition of Continuity:
(i) The continuity of a real function (f) on a subset of the real numbers is
defined when the function exists at point c and is given as-
(ii) A real function (f) is said to be continuous if it is continuous at every point
in the domain of f.
Consider a function f(x), and the function is said to be continuous at every
point in [a, b] including the endpoints a and b.
Continuity of “f” at a means,
Continuity of “f” at b means,

4. Differentiability formula
Assume that if f is a real function and c is a point in its domain. The derivative
of f at c is defined by 0
The derivative of a function f at c is defined by-
Theorem 1: Algebra of continuous functions:
If the two real functions, say f and g, are continuous at a real number c, then
(i) f + g is continuous at x=c.
(ii) f – g is continuous at x=c.
(iii) f. g is continuous at x=c.
(iv)f/g is continuous at x=c, (provided g(c) ≠ 0).
Theorem 2: Suppose f and g are real-valued functions such that (f o g) is
defined at c. If g is continuous at c and if f is continuous at g (c), then (f o g) is

5. Theorem 3: If a function f is differentiable at a point c, then it is also continuous at that point.
Theorem 4 (Chain Rule): Let f be a real-valued function which is a composite of two
functions u and v; i.e., f = v o u.
Suppose t = u(x) and if both dt/dx and dv/dt exist, we have df/dx = (dv/dt). (dt/dx)
Theorem 5:
(1) The derivative of ex
with respect to x is ex
; i.e., d/dx(ex
) = ex
.
(2) The derivative of log x with respect to x is 1/x.
i.e., d/dx(log x) =1/x.
Theorem 6 (Rolle’s Theorem): Let f : [a, b] → R be continuous on [a, b] and differentiable
on (a, b), such that f(a) = f(b), where a and b are some real numbers. Then there exists some c
in (a, b) such that f'(c) = 0.

7. Derivatives of Composite Functions Formula
The derivative of a composite function h(x) = f(g(x)) can be
determined by taking the product of the derivative of f(x) with
respect to g(x) and the derivative of g(x) with respect to the
variable x. Mathematically, the formula for the derivatives of
composite functions is given as:
If f and g
ressed as:
Example 1: Determine the derivative of the composite function
h(x) = (x3
+ 7)10
Solution: Now, let u = x3
+ 7 = g(x), here h(x) can be written as h(x)
= f(g(x)) = u10
. So the derivative of h(x) is given by:

8. d(h(x))/dx = df/du × du/dx
⇒ h'(x) = 10u9
× 3x2
= 10(x3
+ 7)9
× 3x2
= 30 x2
(x3
+ 7)9
Example 2: Derivative of composite function y = sin (cos (x2
))
Solution: y' = cos(cos (x2
)). -sin (x2
)). 2x
= -2x sin (x2
) cos (cos x2
)
Partial Derivatives of Composite Functions in Two Variables
Derivative of a function in many variables is calculated with respect to one of the
variables at a time. Such derivatives are called partial derivatives. We can calculate
the partial derivatives of composite functions z = h(x, y) using the chain rule
method of differentiation for one variable. While determining the partial derivative
of a function with respect to one variable, we consider all remaining variables as
constants. Let us go through an example illustrated below:

9. Example: Find the x and y derivatives of the composite function f(x, y) = (x2
y2
+
ln x)3
Solution: First, we will differentiate the composite function f(x, y) = (x2
y2
+ ln
x)3
with respect to x and consider y as a constant.
∂[(x2
y2
+ ln x)3
]/∂x = 3 (x2
y2
+ ln x)2
× ∂(x2
y2
+ ln x)/∂x
= 3 (x2
y2
+ ln x)2
× (2xy2
+ 1/x)
= 3(2xy2
+ 1/x)(x2
y2
+ ln x)2
Similarly, we will determine the y-derivative considering x as a constant using the
chain rule formula.
∂[(x2
y2
+ ln x)3
]/∂y = 3 (x2
y2
+ ln x)2
× ∂(x2
y2
+ ln x)/∂y
= 3 (x2
y2
+ ln x)2
× (2x2
y)
= 6x2
y (x2
y2
+ ln x)2

10. Important Notes on Derivatives of Composite Functions
•The t-derivative of a composite function z = h(x(t), y(t)) can be calculated using the
formula dh/dt = (∂f/∂x) . (dx/dt) + (∂f/∂y) . (dy/dt)
•Derivative of h(x) w.r.t. x = Derivative of f(x) w.r.t. u × Derivative of u w.r.t. x ⇒
d(h(x))/dx = df/du × du/dx, where h(x) = (f o g)(x) and g(x) = u
Implicit Differentiation Formula
Implicit differentiation is the procedure of differentiating an implicit
equation with respect to the desired variable x while treating the other
variables as unspecified functions of x.
To differentiate an implicit function, any of the following methods is followed
:
•In the first method, the implicit equation is solved for y and it is expressed
explicitly in terms of x and differentiation of y is carried. This method is
found useful only when y is easily expressible in terms of x.
•In the second method, y is thought of as a function of x, and both members
of the implicit equation are differentiated w.r.t x. The resulting equation is
solved to find the value of .

11. Solved Examples
Question 1: Calculate the implicit derivative of
=7
?
Solution:
Given implicit function is,
=7
2x-(5x +5y)+6y =0
(-5x+6y)= -2x+5y
=
=

12. DERIVATIONS OF INVERSE TRIGONOMETRIC FUNCTIONS

15. Example:- Differentiate the Following functions w.r.t.x :-

17. Example 3:-

18. Exponential Function Definition:
An exponential function is a Mathematical function in the form y = f(x) = bx
,
where “x” is a variable and “b” is a constant which is called the base of the
function such that b > 1. The most commonly used exponential function base is
the transcendental number e, and the value of e is equal to 2.71828.
Using the base as “e” we can represent the exponential function as y = ex. This is
called the natural exponential function. However, an exponential function with
base 10 is called the common exponential function.
The exponential function is an important mathematical function which is of the
form
f(x) = ax
Where a>0 and a is not equal to 1.
x is any real number.
If the variable is negative, the function is undefined for -1 < x < 1.
Here,
“x” is a variable
“a” is a constant, which is the base of the function.

19. Exponential Function Derivative
Let us now focus on the derivative of exponential functions.
The derivative of ex
with respect to x is ex
, i.e. d(ex
)/dx = ex
It is noted that the exponential function f(x) =ex
has a special property.
It means that the derivative of the function is the function itself.
(i.e) f ‘(x) = ex
= f(x)
Exponential Series
The exponential series are given below.

20. Exponential Functions Examples
The examples of exponential functions are:
•f(x) = 2x
•f(x) = 1/ 2x
= 2-x
•f(x) = 2x+3
•f(x) = 0.5x
Solved Problems
Question 1:
Simplify the exponential function 2x
– 2x+1
Solution:
Given exponential function: 2x
– 2x+1
By using the property: ax
ay
= ax+y
Hence, 2x+1
can be written as 2x
. 2
Thus the given function is written as:
2x
-2x+1
= 2x
-2x
. 2
Now, factor out the term 2x
2x
-2x+1
= 2x
-2x
. 2 = 2x
(1-2)
2x
-2x+1
= 2x
(-1)
2x
-2x+1
= – 2x
Therefore, the simplification of the given exponential function 2x
– 2x+1
is – 2x
.

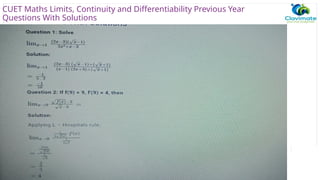
21. Question 2:
Solve the exponential equation: (¼)x
= 64
Solution:
Given exponential equation is:
(¼)x
= 64
Using the exponential rule (a/b)x
= ax
/bx
, we get;
1x
/4x
= 43
1/4x
= 43
[since 1x
= 1]
(1)(4-x
) = 43
4-x
= 43
Here, bases are equal.
So, by equating the powersm we have;
x = -3

22. Practice Questions
1.Graph an exponential function (⅓)x
– 1.
2.Solve for x: 8(4x-1)
= 45x
3.Solve the exponential equation for x: -5x-3
= 25/40
Logarithmic Function Definition:
If the inverse of the exponential function exists then we can represent the
logarithmic function as given below:
Suppose b > 1 is a real number such that the logarithm of a to base b is x if bx
= a.
The logarithm of a to base b can be written as logb a.
Thus, logb a = x if bx
= a.
In other words, mathematically, by making a base b > 1, we may recognise
logarithm as a function from positive real numbers to all real numbers. This
function is known as the logarithmic function and is defined by:
logb : R+
R
→
x log
→ b x = y if by
= x
If the base b = 10, then it is called a common logarithm and if b = e, then it is called
the natural logarithm. Generally, the natural logarithm is denoted by ln.

23. Answer 2:- Using the natural logarithm:
ln(8^(4x-1)) = ln(45^x)
Using the power rule of logarithms, we can bring down the exponent:
(4x-1) ln(8) = x ln(45)
Distribute the ln(8):
4x ln(8) - ln(8) = x ln(45)
Simplify by grouping the x terms on one side and the constant terms on the other:
4x ln(8) - x ln(45) = ln(8)
Factor out x:
x(4 ln(8) - ln(45)) = ln(8)
Divide both sides by the coefficient of x:
x = ln(8) / (4 ln(8) - ln(45))
Simplify by using the properties of logarithms:
x = ln(8) / ln(8^(4) * 45^(-1))
x = ln(8) / ln(2^(12) * 3^(-2))
x = ln(8) / (12 ln(2) - 2 ln(3))
Therefore, x is approximately 0.322.

26. Derivatives of a function in parametric form: There are instances when
rather than defining a function explicitly or implicitly we define it using a third
variable. This representation when a function y(x) is represented via a third
variable which is known as the parameter is a parametric form. A relation
between x and y can be expressible in the form x = f(t) and y = g(t) is a
parametric form representation with parameter as t. Now we will concentrate
on how to differentiate these functions using parametric differentiation.
Parametric Differentiation Questions and Solutions
Example 1: Find the value of for the following functions which are expressed
in the parametric form.
i) x = sin t , y =
ii) x = , y = 3
Solution 1:
i) Since this function is represented in parametric function format beforehand
therefore we need to find out the value
and .
Now,

27. = 2t and = cost
Now with the help of chain rule we can write,
=
This is the required solution of the differentiation of the parametric equation.
ii) These functions are already expressed in terms of t. Therefore, to find
, evaluate and separately.
= 12 =
So =
=

28. Order Derivative Definition and Representation
The second-order derivative is nothing but the derivative of the first derivative of the
given function. So, the variation in speed of the car can be found out by finding out the
second derivative, i.e. the rate of change of speed with respect to time (the second
derivative of distance travelled with respect to the time).
Graphically the first derivative represents the slope of the function at a point, and the
second derivative describes how the slope changes over the independent variable in the
graph. For a function having a variable slope, the second derivative explains the
curvature of the given graph.

29. In this graph, the blue line indicates the slope, i.e. the first derivative of the given function.
And the second derivative is used to define the nature of the given function. For example, we
use the second derivative test to determine the maximum, minimum or the point of inflexion.
Mathematically, if y = f(x)
Then dy/dx = f'(x)
Now if f'(x) is differentiable, then differentiating dy/dx again w.r.t. x we get 2nd
order
derivative, i.e.
Similarly, higher order derivatives can also be defined in the same way like d3
y/dx3
represents a third order derivative, d4
y/dx4
represents a fourth order derivative and so on.
Usually, the second derivative of a given function corresponds to the curvature or concavity
of the graph. If the second-order derivative value is positive, then the graph of a function is
upwardly concave. If the second-order derivative value is negative, then the graph of a
function is downwardly open.
As it is already stated that the second derivative of a function determines the local maximum
or minimum, inflexion point values. These can be identified with the help of below
conditions:
= = f’’(x)

30. •If f”(x) < 0, then the function f(x) has a local maximum at x.
•If f”(x) > 0, then the function f(x) has a local minimum at x.
•If f”(x) = 0, then it is not possible to conclude anything about the point
x, a possible inflexion point.
Second Order Derivative Examples
Let us see an example to get acquainted with second-order derivatives.

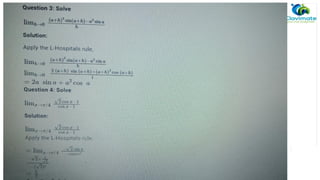
31. What is Mean Value Theorem?
Let us consider, a continuous function f:[a,b]→R which is continuous on the point
[a,b] and differentiable on the point (a,b), some external point exists such as c in (a,b)
such that
f’(c) =
Proof of Mean Value Theorem
The Mean value theorem can be proved considering the function h(x) = f(x) – g(x)
where g(x) is the function representing the secant line AB. Rolle’s theorem can be
applied to the continuous function h(x) and proved that a point c in (a, b) exists such
that h'(c) = 0. This equation will result in the conclusion of mean value theorem.
Consider a line passing through the points, (a, f(a)) and (b, f(b)). Equation of line is
y – f(a) = {f(b) – f(a)}/(b-a) . (x – a)
or y = f(a)+ {f(b) – f(a)}/(b-a) . (x – a)
Let h be a function define difference between any function f and the above line.
h(x) = f(x) – f(a) – {f(b)-f(a)}/(b-a) . (x – a)
using “Rolle’s theorem”, we have
h'(x) = f'(x) – {f(b)-f(a)}/(b-a)
Or f(b) – f(a) = f'(x) (b – a). Hence Proved.

32. Application of Mean Value Theorem
Mean value theorem is the relationship between the derivative of a function and
increasing or decreasing nature of function. It basically defines the derivative of a
differential and continuous function. Below are few important results used in mean
value theorem.
1. Let the function be f such that it is, continuous in interval [a,b] and differentiable on
interval (a,b), then
f'(x) = 0, x (a,b), then f(x) is constant in [a,b].
∈
2. Let f and g be a functions such that, f and g are continuous in interval [a,b] and
differentiable on interval (a,b),
f'(x) = g'(x), x (a,b), then f(x) – g(x) is constant in [a,b]
∈
3. Strictly Increasing Function
Let the function be f such that, continuous in interval [a, b] and differentiable in
interval(a,b)
f'(x) > 0, x (a,b), then f(x) is strictly increasing function in [a,b]
∈
4. Strictly Decreasing Function
Let the function be f such that, continuous in interval [a,b] and differentiable in
interval (a, b)
f'(x) < 0, x (a,b), then f(x) is strictly decreasing function in [a,b].
∈

33. Statement:
Let f and g be functions defined on [a,b] such that both are continuous in closed interval [a,b]
and are differentiable in open interval (a,b)
then there exists at least one point c (a,b) such that
∈
If we take g(x) = x for every x {a,b] in Cauchy’s mean value theorem, we get
∈
f’(c) = which is Langrange’s mean value theorem. This is also called an extended mean value
theorem.
Questions on these Problems:-
Cauchy Mean Value Theorem
.

35. 2(c – 1) = 1 which gives the solution as c = 3/2 which lies in the given interval [1, 3].
Question 2: Verify Rolle’s theorem for the function f(x) = x2
– 8x + 12 on (2, 6).
Solution:
Since a polynomial function is continuous and differentiable everywhere, f(x) is differentiable and
continuous conditions of Rolle’s theorem is satisfied.
f (2) = 22
– 8 (2) + 12 = 0
f (6) = 62
– 8(6) + 12 = 0
This implies, f(2) = f(3)
Therefore, Rolle’s theorem is applicable for the given function f(x).
There must exist c (2, 6) such that f'(c) = 0
∈
f'(x) = 2x – 8
f'(c) = 2c – 8
2c – 8 = 0
c = 4 (2,6)
∈
Therefore, Rolle’s theorem is verified.

36. CUET Maths Limits, Continuity and Differentiability Previous Year
Questions With Solutions

39. Q1. Determine the value of ‘k’ for which the following function is continuous at x
= 3:

40. Q2.Find the values of p and q for which is continuous at x = .

42. THANK YOU
֍֍֍֍