Course: MCA Subject: Computer Oriented Numerical Statistical Methods Unit-2 Solution of simultaneous Linear Equations RAI UNIVERSITY, AHMEDABAD

1. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 1
Course: MCA
Subject: Computer Oriented Numerical
Statistical Methods
Unit-2
RAI UNIVERSITY, AHMEDABAD

2. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 2
Unit-II-Solution of simultaneous Linear Equations
Sr.
No.
Name of the Topic Page
No.
1. Introduction, System of linear equations in two variable Methods
for solving linear equation,
2
2. Existence of Unique roots, multiple roots and no roots (consistency
and Inconsistency of system), Dependent and Independent system
of linear equations, Examples
2
3. System of linear equations in three variables, System of linear
equations in n-variables
7
4. Methods for solving system of linear equations 9
5. Gauss elimination method and its examples 9
6. Gauss Seidel method and its examples 13
7. Difference between Direct Method and Iterative Method 16
8. References 17
9. Exercise 18

3. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 3
1.1 Introduction:
We are already familiar with solving linear equations of one variable and two
variables. The general form of linear equation of one variable is ax + b = 0 where
a is not 0 and a and b are real numbers, and the general form of linear equations of
two variables is
ax + by + c =0 where a, b and c are real numbers. In this section let us discuss with
system of linear equations.
1.2 What is a system of linear Equations?
1.2.1 Definition:System of Linear Equations
Linear Equations in one variable: The general form of linear equation in one
variable is ax + b = 0, where a and b are Real numbers and a is not equal to 0.
This system has unique solution, which is x = - b/a
For example : 2x + 6 = 0
=> 2x = -6
= > x = - 6/2 = - 3 𝑥 =
−𝑏
𝑎
The only solution to this equation is x = - 3
This solution can be represented on a number line.
2.1 System of linear Equations in two variables:
The general form of linear equation in two variables is ax + by +c = 0, where
a, b, c are real numbers and a and b bothnot equal to 0.
Let us consider the example x + y = 6
This equation will satisfy for infinitely many pairs of the form (x,y) satisfying this
condition.
For example (1,6), 2,4), (3,3), (7, -1),.........etc
so that in all the cases x + y = 5, meaning the sum of the coordinates = 6
Hence these pairs of values satisfying the given equation are called the solution to
the given equation.

4. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 4
2.2 System of linear Equations Solver:
Step-1. For the linear equations of one variable, there will be unique solution
which can be solved from the given equation.
Step-2. For the linear equations of two variables, we need to have two equations to
solve for the variables.
Let us assume that the given two equations are of the form
a1 x + b1 y + c1 = 0 and a2 x + b2 y + c2 = 0.
It is possible to solve the system of linear equations for the unknown variables x
and y.
The methods involved in solving these homogeneous systems of linear equations
are,
1. Substitution Method.
2. Elimination Method.
3. Cross Multiplication Method
4. Matrix Method etc.
To solve a system of linear equations we should know about the types of
solution(s) that exists for the system.
2.3 Consistentsystemof linear equations: (Unique Roots, Infinite Roots)
The system of linear equations is said to be consistent if the solution exists.
For the above system of equations, if the following ratio satisfies we can say about
the type of solutions accordingly.
If
𝑎1
𝑎2
≠
𝑏1
𝑏2
then the system has unique solution.
If
𝑎1
𝑎2
=
𝑏1
𝑏2
=
𝑐1
𝑐2
then the system has infinite solution.
2.4 InconsistentSystem of Equations: (No roots)
The system of linear equations is said to be inconsistent if the solution
does not exists.
For the above system of equations, if the following ratio satisfies then we can say
that the system is inconsistent

5. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 5
If
𝑎1
𝑎2
=
𝑏1
𝑏2
≠
𝑐1
𝑐2
2.5 Dependent systemof Linear Equations:
System of Linear Equations is said to be dependent if both the equations have
infinitely common solutions.
So the coinciding lines are the dependent system of linear equations.
They satisfy the condition,
𝑎1
𝑎2
=
𝑏1
𝑏2
=
𝑐1
𝑐2
2.6 Independent system of Linear Equations:
System of Linear Equations is said to be independent if they do not
have infinite number of common solution.
So the intersecting lines and the parallel lines are the Independent system of Linear
Equations.
2.7 Solving systemof linear equations:
While solving a system of linear equations, we will come to know if they are
consistent or inconsistent, dependent or independent.
System of Linear Equations Examples:
2.7.1 Example—
Solve the systemof linear equations: 𝟐𝒙 + 𝟑𝒚 = 𝟐𝟓; 𝟑𝒙 + 𝟐𝒚 = 𝟐𝟓
Solution:
Let us number the equations
2𝑥 + 3𝑦 = 25 ------------------------------(1)
3𝑥 + 2𝑦 = 25 ------------------------------(2)
Multiplying Equation (1) by 3, 3 ( 2𝑥 + 3𝑦 ) = 3 ( 25)
6𝑥 + 9𝑦 = 75 --------------------(3)
Multiplying equation (2) by 2, 2 ( 3𝑥 + 2𝑦 ) = 2 ( 25)
6𝑥 + 4𝑦 = 50 -----------------------------(4)
6𝑥 + 9𝑦 = 75 ------------------------------(3)
6𝑥 + 4𝑦 = 50 ------------------------------(4)
______________

6. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 6
Subtracting (4) from (3) 5𝑦 = 25
𝑦 = 25 /5 = 5
Substituting y=5 in (1) we get, 2𝑥 + 3(5) = 25
2𝑥 + 15 = 25
2𝑥 = 25 − 15 = 10
𝑥 = 10/2 = 5
Therefore, the two equations intersect at the point (2,2).
Hence the system of equations is consistent and independent.
If we verify the condition,
𝑎1
𝑎2
≠
𝑏1
𝑏2
, we see that,
2
3
≠
3
2
2.7.2 Example—
Solve the System of linear equations: 𝒙 + 𝒚 = 𝟒, 𝟐𝒙 + 𝟐𝒚 = 𝟗
Solution:
Let 𝑥 + 𝑦 = 4 ---------------------(1)
2𝑥 + 2𝑦 = 9 ------------------- (2)
Multiplying (1) by 2, we get,
2 ( 𝑥 + 𝑦 ) = 2(4)
=> 2𝑥 + 2𝑦 = 8 -------------------(3)
2𝑥 + 2𝑦 = 9 --------------------(2)
Subtracting , (2) from (3), we get, 0 = 1, which is not true.
Hence the system of equations have no solution.
From the above relation,
𝑎1
𝑎2
=
𝑏1
𝑏2
≠
𝑐1
𝑐2
we have
1
2
=
1
2
≠
4
9
Hence the above pair of equations is inconsistent and
independent.

7. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 7
2.7.3 Example—
Solve the system of linear equations: 𝒙 + 𝟑𝒚 = 𝟖 ; 𝟑𝒙 + 𝟗𝒚 = 𝟐𝟒
Solution:
Let 𝑥 + 3𝑦 = 8 ---------------------(1)
3𝑥 + 9𝑦 = 24 ------------------ (2)
Substituting 𝑥 = 8 − 3𝑦 in (2), 3 ( 8 − 3𝑦 ) + 9𝑦 = 24
=> 24 − 9𝑦 + 9𝑦 = 24
This condition is true for all values of y.
we get 24 = 24 which is true.
Therefore the system of equations has infinitely many solutions.
Hence the system is consistent and dependent Hence by solving system of
equations we can conclude if the system of linear equations is consistent or
inconsistent and independent or dependent.
2.8 System of Linear Equations word problems:
We can follow the following steps while solving the word problems.
Step 1: Read the problem carefully and identify the unknown quantities. Give
these quantities a variable name like 𝑥, 𝑦, 𝑢, 𝑣, 𝑤, etc.
Step 2: Identify the variables to be determined.
Step 3: Read the problem carefully and formulate the equations in terms of the
variables to be determined.
Solve 4: Solve the equations obtained in step 3, using any one of the method you
are comfortable with.
2.8.1 Example—
4 Chairs and 3 tables cost1400 dollars and 5 chairs and 2 tables cost1400
dollars. Find the costof a chair and a table.
Solution:
Let the costof a chair be x dollars, and the costof a table be y dollars.

8. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 8
Let us solve linear system of equations we have framed here.
Hence we have the equations, 4𝑥 + 3𝑦 = 1400 ---------------------(1)
5𝑥 + 2𝑦 = 1400 ---------------------(2)
Multiplying (1) by 5, 5( 4𝑥 + 3𝑦 ) = 5( 1400)
=> 20 𝑥 + 15 𝑦 = 7000------------------------(3)
Multiplying (2) by 4, we get 4 ( 5𝑥 + 2𝑦 ) = 4 ( 1400)
=> 20 𝑥 + 8 𝑦 = 5600 ----------------------(4)
20 𝑥 + 15 𝑦 = 7000----------------------(3)
______________________
Subtracting (3) from (4), − 7 𝑦 = −1400
=> 𝑦 = −1400/−7 = 200
Substituting y= 200 in Equation (1), we get,
4𝑥 + 3 ( 200) = 1400
=> 4𝑥 + 600 = 1400
=> 4𝑥 = 1400 − 600 = 800 =
> 𝑥 = 800/4 = 200
Therefore costof a Chair is 200 dollars and costof a Table is 200 dollars.
3.1 System of linear equations in three variables:
The general form of linear equation in three variables, 𝑥, 𝑦 𝑎𝑛𝑑 𝑧is
𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 + 𝑑 = 0, where a, b, c are real numbers and a, b, c not all equal
to 0.
This represent the equation of a plane in three-dimensional co-ordinate system,
where 𝑎, 𝑏, 𝑐 are the direction ratios of the normal to the plane.
To solve the equation in three variables, we need to have three conditions
(equations) relating the variables 𝑥, 𝑦 𝑎𝑛𝑑 𝑧.
Elimination method is the most suitable method to solve the equations.

9. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 9
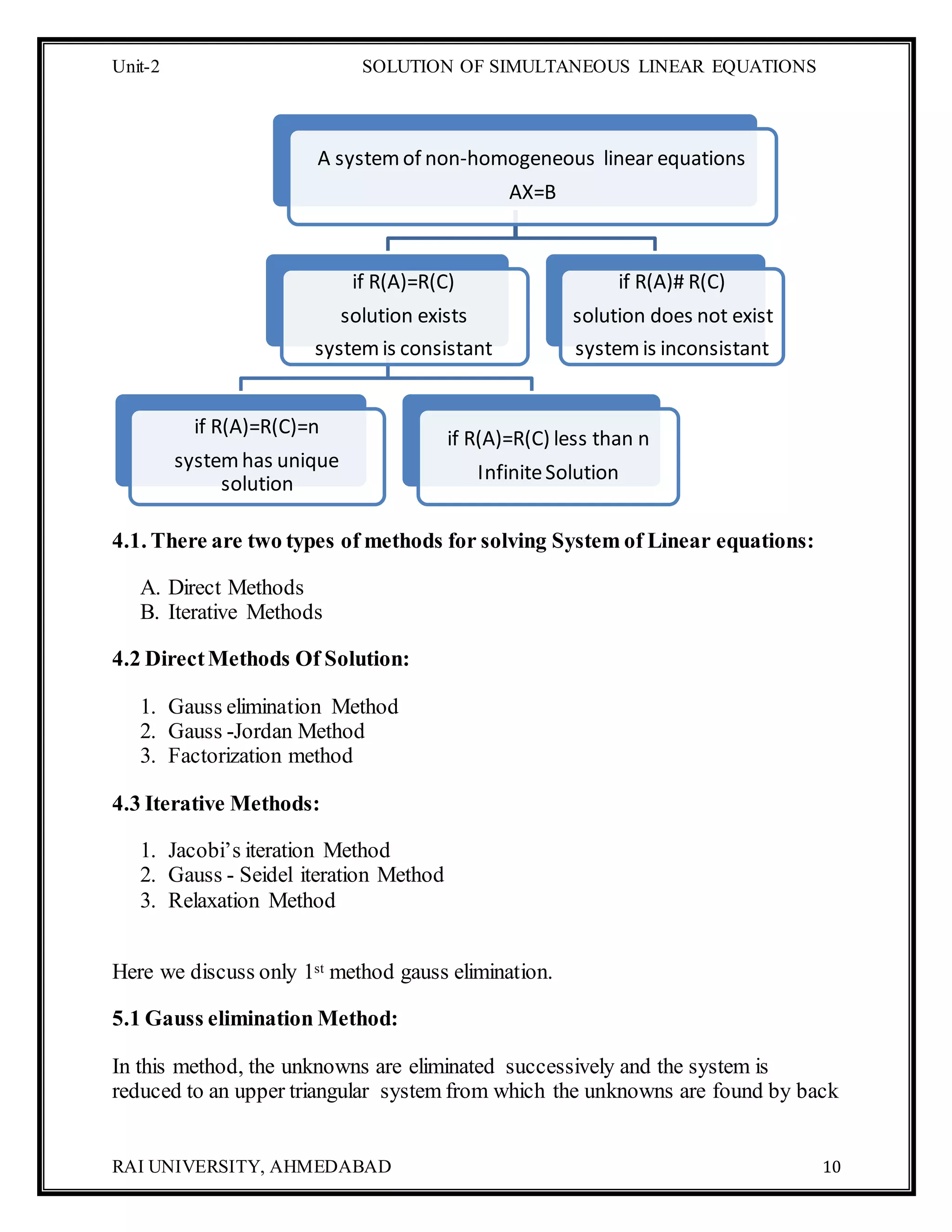
3.2 System of Linear equations with n variables
𝑎11 𝑥1 + 𝑎12 𝑥2 + ⋯… …+ 𝑎1𝑛 𝑥 𝑛 = 𝑏1
𝑎21 𝑥1 + 𝑎22 𝑥2 + ⋯… …+ 𝑎2𝑛 𝑥 𝑛 = 𝑏2
…………… ………………… ………………..
𝑎 𝑚1 𝑥1 + 𝑎 𝑚2 𝑥2 + ⋯… …+ 𝑎 𝑚𝑛 𝑥 𝑛 = 𝑏 𝑚
We can also write it in Matrix form as
[
𝑎11 𝑎12 ……. 𝑎1𝑛
𝑎21 𝑎22 ……. 𝑎2𝑛
…… . . …… …… ……. .
𝑎 𝑚1 𝑎 𝑚2 …… 𝑎 𝑚𝑛
] [
𝑥1
𝑥2
…
𝑥 𝑚
] = [
𝑏1
𝑏2
…
𝑏3
]
⟹ 𝐴𝑋 = 𝐵
𝐶 = [ 𝐴, 𝐵] = [
𝑎11 𝑎12 … …. 𝑎1𝑛
𝑎21 𝑎22 ……. 𝑎2𝑛
…… .. ……… … … …. .
𝑎 𝑚1 𝑎 𝑚2 …… 𝑎 𝑚𝑛
]is called augumented matrix.
[ 𝐴: 𝐵] = 𝐶
3.2.1 (𝒂) ConsistentEquations:
If Rank A = Rank C
(i) Unique Solution: Rank A= Rank C=n Where, 𝑛 = number of
unknown
(ii) Infinite Solution: Rank A= Rank C= r, 𝑟 < 𝑛
3.2.2 (𝒃) InconsistentEquations:
If Rank 𝐴 ≠ Rank 𝐶.

10. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 10
4.1. There are two types of methods for solving System of Linear equations:
A. Direct Methods
B. Iterative Methods
4.2 DirectMethods Of Solution:
1. Gauss elimination Method
2. Gauss -Jordan Method
3. Factorization method
4.3 Iterative Methods:
1. Jacobi’s iteration Method
2. Gauss - Seidel iteration Method
3. Relaxation Method
Here we discuss only 1st method gauss elimination.
5.1 Gauss elimination Method:
In this method, the unknowns are eliminated successively and the system is
reduced to an upper triangular system from which the unknowns are found by back
A system of non-homogeneous linear equations
AX=B
if R(A)=R(C)
solution exists
systemis consistant
if R(A)=R(C)=n
systemhas unique
solution
if R(A)=R(C) less than n
InfiniteSolution
if R(A)# R(C)
solution does not exist
systemis inconsistant

11. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 11
substitution. The method is quite general and is well-adapted for computer
operations. Here we shall explain it by considering a system of three equations for
the sake of clarity.
Consider the equations
𝑎1 𝑥 + 𝑏1 𝑦 + 𝑐1 𝑧 = 𝑑1
𝑎2 𝑥 + 𝑏2 𝑦 + 𝑐2 𝑧 = 𝑑2
𝑎3 𝑥 + 𝑏3 𝑦 + 𝑐3 𝑧 = 𝑑3
Step-I. To eliminate 𝑥 from second and third equations.
Assuming 𝑎1 ≠ 0,we eliminate 𝑥 from the second equation by subtracting (
𝑎2
𝑎1
)
times the first equation from the second equation. Similarly we eliminate 𝑥 from
the third equation by eliminating (
𝑎3
𝑎1
) times the first equation from the third
equation. We thus get the new system
𝑎1 𝑥 + 𝑏1 𝑦 + 𝑐1 𝑧 = 𝑑1
𝑏2′𝑦 + 𝑐2′𝑧 = 𝑑2′
𝑏3′𝑦 + 𝑐3′𝑧 = 𝑑3′
Here the first equation is called the pivotal equation and 𝑎1 is called the first pivot.
Step-II. To eliminate 𝑦 from third equation in (2).
Assuming 𝑏2′ ≠ 0, we eliminate 𝑦 from the third equation of (2) ,by Subtracting
(
𝑏3′
𝑏2′
) times the second equation from third equation. We thus, get the new system
𝑎1 𝑥 + 𝑏1 𝑦 + 𝑐1 𝑧 = 𝑑1
𝑏2′𝑦 + 𝑐2′𝑧 = 𝑑2′
𝑐3′′𝑧 = 𝑑3′′
Here the second equation is the pivotal equation and 𝑏2′ is the new pivot.

12. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 12
Step-III. To evaluate the unknowns.
The values of 𝑥, 𝑦, 𝑧 are found from the reduced system (3) by back substitution.
5.1.1 Example—
Apply gauss elimination method to solve the equations
𝒙 + 𝟒𝒚 − 𝒛 = −𝟓
𝒙 + 𝒚 − 𝟔𝒛 = −𝟏𝟐
𝟑𝒙 − 𝒚 − 𝒛 = 𝟒 .
Solution:
We have [
1 4 −1
1 1 −6
3 −1 −1
][
𝑥
𝑦
𝑧
] = [
−5
−12
4
]
Operate 𝑅2 − 𝑅1 & 𝑅3 − 3𝑅1,
~ [
1 4 −1
0 −3 −5
0 −13 2
][
𝑥
𝑦
𝑧
] = [
−5
−7
19
]
Operate 𝑅3 −
13
3
𝑅2,
[
1 4 1
0 −3 −5
0 0 71/3
][
𝑥
𝑦
𝑧
] = [
−5
−7
148/3
]
Thus, We have 𝑧 =
148
71
= 2.0845,
3𝑦 = 7 − 5𝑧 = 7 − 10.4225 = −3.4225 i.e., 𝑦 = −1.1408
𝑥 = −5 − 4𝑦 + 𝑧 = −5 + 4(1.1408) + 2.0845 = 1.6479
and
Hence 𝑥 = 1.6479, 𝑦 = −1.1408, 𝑧 = 2.0845.

13. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 13
5.1.2 Example—
Solve by using gauss elimination Method.
𝒙 𝟏 + 𝟐𝒙 𝟐 − 𝒙 𝟑 = 𝟑
𝟑𝒙 𝟏 − 𝒙 𝟐 + 𝟐𝒙 𝟑 = 𝟏
𝟐𝒙 𝟏 − 𝟐𝒙 𝟐 + 𝟑𝒙 𝟑 = 𝟐
𝒙 𝟏 − 𝒙 𝟐 + 𝒙 𝟑 = −𝟏
Solution:
We have given system of solution
𝑥1 + 2𝑥2 − 𝑥3 = 3
3𝑥1 − 𝑥2 + 2𝑥3 = 1
2𝑥1 − 2𝑥2 + 3𝑥3 = 2
𝑥1 − 𝑥2 + 𝑥3 = −1
The System of equation can be written in matrix form as
[
1 2 −1
3 −1 2
2
1
−2
−1
3
1
][
𝑥1
𝑥2
𝑥3
] = [
3
1
2
−1
]
Operate (−3) 𝑅1 + 𝑅2, (−2) 𝑅1 + 𝑅3, (−1) 𝑅1 + 𝑅4
~[
1 2 −1
0 −7 5
0
0
−6
−3
5
2
][
𝑥1
𝑥2
𝑥3
] = [
3
−8
−4
−4
]
Operate −
6
7
𝑅2 + 𝑅3 , −
3
7
𝑅2 + 𝑅4

14. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 14
~[
1 2 −1
0 −7 5
0
0
0
0
5/7
−1/7
][
𝑥1
𝑥2
𝑥3
] = [
3
−8
20/7
−4/7
]
Operate
1
5
𝑅3 + 𝑅4
~[
1 2 −1
0 −7 5
0
0
0
0
5/7
0
][
𝑥1
𝑥2
𝑥3
] = [
3
−8
20/7
0
]
∴
5
7
𝑥3 =
20
7
⟹ 𝑥3 = 4
Now −7𝑥2 + 5𝑥3 = −8
⟹ −7𝑥2 + 5(4) = −8
⟹ −7𝑥2 = −28
⟹ 𝑥2 = 4
Now 𝑥1 + 2𝑥2 − 𝑥3 = 3
⟹ 𝑥1 + 2(4) − 4 = 3
⟹ 𝑥1 = 3 + 4 − 8
⟹ 𝑥1 = −1
Hence we get the solution set (𝑥1,𝑥2, 𝑥3) = (4,4,−1)
Now we discuss about 2nd iterative method Gauss – Seidel.
6.1 Gauss - Seidel iteration Method:

15. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 15
This is a modification of the Jacobi’s iteration method. As before, we start with
initial approximations 𝑥0, 𝑦0, 𝑧0 (each=0) for 𝑥, 𝑦, 𝑧 respectively. Substituting 𝑦 =
𝑦0, 𝑧 = 𝑧0 in the first equations, we get
𝑥1 = 𝑘1
Then putting 𝑥 = 𝑥1, 𝑧 = 𝑧0 in the second of the equations, we have
𝑦1 = 𝑘2 − 𝑙2 𝑥1 − 𝑚2 𝑧0
Next substituting 𝑥 = 𝑥1, 𝑦 = 𝑦1 in the third equations, we obtain
𝑧1 = 𝑘3 − 𝑙3 𝑥1 − 𝑚3 𝑦1
And so on, i.e. as soonas new approximation for an unknown is found, it is
immediately used in the next step.
This process ofiteration is continued till convergency to the desired degree of
accuracy is obtained.
6.1.1 Example—
Apply Gauss-Seideliterationmethod to solve the equation:
𝟐𝟎𝒙 + 𝒚 − 𝟐𝒛 = 𝟏𝟕
𝟑𝒙 + 𝟐𝟎𝒚 − 𝒛 = −𝟏𝟖
𝟐𝒙 − 𝟑𝒚 + 𝟐𝟎𝒛 = 𝟐𝟓
Solution:
We write the given equation in the form
𝑥 =
1
20
(17 − 𝑦 + 2𝑧) ……………………………… (1)
𝑦 =
1
20
(−18− 3𝑥 + 𝑧) ……………………………… (2)
𝑧 =
1
20
(25 − 2𝑥 + 3𝑦) ………………………………. (3)

16. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 16
We start form the approximation 𝑥0 = 𝑦0 = 𝑧0 = 0.substituting 𝑦 = 𝑦0, 𝑧 = 𝑧0 in
the right side of the first of equations (1) we get
𝑥1 =
1
20
(17− 𝑦0 + 2𝑧0) = 0.8500
Putting 𝑥 = 𝑥1, 𝑧 = 𝑧0 in the second of the equations (1), we have
𝑦1 =
1
20
(−18 − 3𝑥1 + 𝑧0) = −1.0275
Putting 𝑥 = 𝑥1, 𝑦 = 𝑦1 in the last of the equations (1), we obtain
𝑧1 =
1
20
(25− 2𝑥1 + 3𝑦1) = 1.0109
For the second iteration, we have
𝑥2 =
1
20
(17 − 𝑦1 + 2𝑧1) = 1.0025
𝑦2 =
1
20
(−18 − 3𝑥2 + 𝑧1) = −0.9998
𝑧2 =
1
20
(25− 2𝑥2 + 3𝑦2) = 0.9998
For the third iteration, we get
𝑥3 =
1
20
(17 − 𝑦2 + 2𝑧2) = 1.0000
𝑦3 =
1
20
(−18 − 3𝑥3 + 𝑧2) = −1.0000
𝑧3 =
1
20
(25− 3𝑥3 + 2𝑦3) = 1.0000
The values in the 2nd and 3rd iterations bring practically the same, we can stop.
Hence the solution is 𝑥 = 1, 𝑦 = −1, 𝑧 = 1.

17. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 17
7.1 Difference betweendirect and iterative methods:
Direct Method Iterative Method
It computes the solution to a problem in
a finite number of steps.
In contrast to direct methods, iterative
methods are not expected to terminate in
a number of steps.
These methods give the precise answer
if they were performed in infinite
precision arithmetic.
Iterative methods form successive
approximations that converge to the
exact solution in the limit.
This method takes less time for
computation when we have small
system linear of equations.
This method takes long time for
calculation when we have small system
of linear equations.
When we have large linear system of
equation Iterative method became more
easy then direct method.
Iterative methods are better than direct
methods for solving large linear systems
e.g. Gauss elimination, LU
decomposition
e.g. Gauss -Seidel method, Jacobi
Method, Newton-Raphson method.

18. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 18
8. Referencesandwebsite Name:
1. Higher Engineering mathematics by B.S.Grewal
2. Higher Engineering Mathematics by B.V.Ramana
3. http://www.linearequations.org/system-of-linear-equations.html#
4. http://www.mathworks.com/matlabcentral/answers/7058-are-iterative-
methods-always-better-than-direct-methods-for-solving-large-linear-systems
5. http://1.bp.blogspot.com/-
pHo8nT2SKgM/UPKdqSinfSI/AAAAAAAAC9I/JZHDxmqADsg/s1600/dir
ect_vs_indirect.png

19. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 19
EXERCISE
Q-1 Evaluate the following questions:
1. Solve the following system of linear equation
𝑥 + 4𝑦 = −10 ,3𝑥 − 𝑦 = 9
2. Solve the following system of linear equation
3𝑥 + 7𝑦 = 15,5𝑥 + 2𝑦 = −4
3. Show that the non Homogeneous system of linear equation are not
consistant.
2𝑥 + 6𝑦 = −11
6𝑥 + 20𝑦 − 6𝑧 = −3
6𝑦 − 18𝑧 = −1
4. Test the consistency of the following equations and solve them if possible.
3𝑥 + 3𝑦 + 3𝑧 = 1
𝑥 + 2𝑦 = 4
10𝑦 + 3𝑧 = −2
2𝑥 − 3𝑦 − 𝑧 = 5
Q-2 Evaluate the following questions:
1. Solve the following equations by Gauss elimination method:
2𝑥 + 𝑦 + 𝑧 = 10
3𝑥 + 2𝑦 + 3𝑧 = 18
𝑥 + 4𝑦 + 9𝑧 = 16
2. Solve the following equations by Gauss elimination method:
2𝑥 − 𝑦 + 3𝑧 = 9

20. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 20
𝑥 + 𝑦 + 𝑧 = 6
𝑥 − 𝑦 + 𝑧 = 2
3. Solve the following equations by Gauss-Seidel method:
2𝑥 + 𝑦 + 6𝑧 = 9
8𝑥 + 3𝑦 + 2𝑧+ 13 = 0
𝑥 + 5𝑦 + 𝑧 = 7
4. Solve the following equations by Gauss-Seidel method:
28𝑥 + 4𝑦 − 𝑧 = 32
𝑥 + 3𝑦 + 10𝑧 = 24
2𝑥 + 17𝑦 + 4𝑧 = 35

21. Unit-2 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS
RAI UNIVERSITY, AHMEDABAD 21