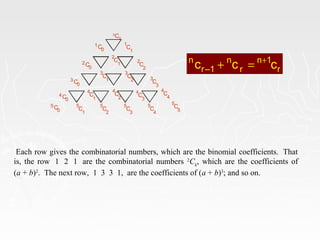
The document discusses the binomial theorem, which provides a method for expanding binomial expressions and calculating their coefficients without direct multiplication. It details the structure of binomials, Pascal's triangle, and the properties of binomial coefficients in expansions, providing examples and explanations for terms and calculations. The binomial theorem is applicable to any positive integer power of a binomial and reveals the symmetry of coefficients in the expansion.

2. Presented ByPresented By
Group-JGroup-J
MD. Habibur Rahman (41222009)MD. Habibur Rahman (41222009)
Md. Obaidur Rahman Sikder (41222041)Md. Obaidur Rahman Sikder (41222041)
Binomial TheoremBinomial Theorem

3. A binomial is an algebraic expression containing 2 terms. For example, (x + y) is a
binomial.
We sometimes need to expand binomials as follows:
(a + b)0
= 1
(a + b)1
= a + b
(a + b)2
= a2
+ 2ab + b2
(a + b)3
= a3
+ 3a2
b + 3ab2
+ b3
(a + b)4
= a4
+ 4a3
b + 6a2
b2
+ 4ab3
+ b4
(a + b)5
= a5
+ 5a4
b + 10a3
b2
+ 10a2
b3
+ 5ab4
+ b5
Clearly, doing this by direct multiplication gets quite tedious and can be rather
difficult for larger powers or more complicated expressions.
BinomialsBinomials

4. In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a
triangle. It is named after the French mathematician Blaise Pascal in much of the
Western world, although other mathematicians studied it centuries before him in India,
Greece, Iran, China, Germany, and Italy.
Pascal’s trianglePascal’s triangle
3
4
5
6
10
1
1
1
1
1
1
1
2
3
4
10 5
1 1
1 1
( )0
a b 1+ =
( )1
a b 1a 1b+ = +
( )2 2 2
a b 1a 2ab 1b+ = + +
( )3 3 2 2 3
a b 1a 3a b 3ab 1b+ = + + +
( )4 4 3 2 2 3 4
a b 1a 4a b 6a b 4ab 1b+ = + + + +
( )5 5 4 3 2 2 3 4 5
a b 1a 5a b 10a b 10a b 5ab 1b+ = + + + + +

5. 0
C0
1C0 C
1
1
C
2
2
C
3
3
C
4
4
C
5
5
C
2
1
C
3
1
C
4
1
C
5
1
C
5
2
C
5
3
C
5
4
C
4
3
C
3
2
C
4
2
2C0
3C0
4C0
5C0
n n n 1
r–1 r rc c c+
+ =
Each row gives the combinatorial numbers, which are the binomial coefficients. That
is, the row 1 2 1 are the combinatorial numbers 2
Ck
, which are the coefficients of
(a + b)2
. The next row, 1 3 3 1, are the coefficients of (a + b)3
; and so on.

6. Properties of binomial expansion (a+b)Properties of binomial expansion (a+b)nn
( )n n n 0 n n–1 1 n n–2 2 n 1 n–1 n 0 n
0 1 2 n–1 na b c a b c a b c a b ... c a b c a b+ = + + + + +
 Based on the binomial properties, the binomial theorem states that the following
binomial formula is valid for all positive integer values of n.
 (a+b)n
has n+1 terms as 0 ≤ k ≤ n.
 The first term is an
and the final term is bn
 Progressing from the first term to the last, the exponent of a decreases by from
term to term (start at n and go down) while the exponent of b increases by (start
at 0 and go up).
 The sum of the exponents of a and b in each term is n.
 If the coefficient of each term is multiplied by the exponent of a in that term, and
the product is divided by the number of that term, we obtain the coefficient of the
next term.
 Coefficients of terms equidistant from beginning and end is same as n
ck = n
cn-k

7. Example: What is (x+5)4
Start with
exponents:
x4
50
x3
51
x2
52
x1
53
x0
54
Include
Coefficients:
1x4
50
4x3
51
6x2
52
4x1
53
1x0
54
Then write down the answer (including all calculations, such as 4×5, 6×52
, etc):
(x+5)4
= x4
+ 20x3
+ 150x2
+ 500x + 625
 The nth row of the Pascal's Triangle will be the coefficients of the expanded binomial.
 For each line, the number of products (i.e. the sum of the coefficients) is equal to 2n
.
 For each line, the number of product groups is equal to n+1. .
 The binomial theorem can be applied to the powers of any binomial.
For example,
 For a binomial involving subtraction, the theorem can be applied as long as the opposite
of the second term is used. This has the effect of changing the sign of every other term
in the expansion:

8. According to the theorem, it is possible to expand any power of x+ y into a sum of the
form
where each is a specific positive integer known as binomial coefficient. This formula
is also referred to as the Binomial Formula or the Binomial Identity. Using summation
notation, it can be written as
The final expression follows from the previous one by the symmetry of x and y in the first
expression, and by comparison it follows that the sequence of binomial coefficients in the
formula is symmetrical.
A variant of the binomial formula is obtained by substituting 1 for y, so that it involves
only a single variable. In this form, the formula reads
or equivalently
Statement of the theoremStatement of the theorem

9. THE BINOMIAL THEOREM shows how to calculate a power of a binomial –
(x+ y)n
-- without actually multiplying out.
For example, if we actually multiplied out the 4th power of (x + y) --
(x + y)4
= (x + y) (x + y) (x + y) (x + y)
-- then on collecting like terms we would find:
(x + y)4
= x4
+ 4x3
y + 6x2
y2
+ 4xy3
+ y4
. . . . . (1)
Notice: The literal factors are all the combinations of a and b where the sum of the
exponents is 4: x4
, x3
y, x2
y2
, xy3
, y4
.
The degree of each term is 4.
The first term is actually x4
y0
, which is x4
· 1.
Statement of the theoremStatement of the theorem

10. Thus to "expand" (x + y)5
, we would anticipate the following terms, in which the sum of
all the exponents is 5:
(x + y)5
= ? x5
+ ? x4
y + ? x3
y2
+ ? x2
y3
+ ? xy4
+ ? y5
The question is, What are the coefficients?
They are called the binomial coefficients.
(x + y)4
= x4
+ 4x3
y + 6x2
y2
+ 4xy3
+ y4
In the expansion of (x + y)4
, the binomial coefficients are 1 4 6 4 1 .
Note the symmetry: The coefficients from left to right are the same right to left.
The answer to the question, "What are the binomial coefficients?" is called the binomial
theorem. It shows how to calculate the coefficients in the expansion of (x+ y)n
.
Statement of the theoremStatement of the theorem

11. The symbol for a binomial coefficient is . The upper index n is the exponent of the
expansion; the lower index k indicates which term, starting with k = 0.
The lower index k is the exponent of y.
For example, when n = 5, each term in the expansion of (x + y)5
will look like this:
x5 − k
yk
k will successively take on the values 0 through 5.
(x + y)5
= x5
+ x4
y + x3
y2
+ x2
y3
+ xy4
+ y5
Again, each lower index is the exponent of y. The first term has k = 0, because in the
first term, y appears as y0
, which is 1.
Statement of the theoremStatement of the theorem

12. Now, what are these binomial coefficients, ?
The theorem states that the binomial coefficients are none other than the combinatorial
numbers, n
Ck
.
= n
Ck
(a + b)5 = 5
C0
a5
+ 5
C1
a4
b + 5
C2
a3
b2
+ 5
C3
a2
b3
+ 5
C4
ab4
+ 5
C5
b5
=
1a5
+ a4
b + a3
b2
+ a2
b3
+ ab4
+ b5
=
a5
+ 5a4
b + 10a3
b2
+ 10a2
b3
+ 5ab4
+ b5
The binomial coefficients here are 1 5 10 10 5 1.
Statement of the theoremStatement of the theorem
Note: The coefficient of the first term is 1, and the coefficient of the second term is
the same as the exponent of (a + b), which here is 5.

13. Using sigma notation, and factorials for the combinatorial numbers, here is the
binomial theorem for (a+b)n
:
What follows the summation sign is the general term. Each term in the sum will look
like that -- the first term having k = 0; then k = 1, k = 2, and so on, up to k = n.
Notice that the sum of the exponents (n − k) + k, always equals n.
Statement of the theoremStatement of the theorem
Example 1.
a) The term a8
b4
occurs in the expansion of what binomial?
Answer. (a + b)12
. The sum of 8 + 4 is 12.
b) In that expansion, what number is the coefficient of a8
b4
?
Answer. It is the combinatorial number,
12
C4
=
12· 11· 10· 9
1· 2· 3· 4
= 495
Note: The lower index, in this case 4, is the exponent of b.
This same number is also the coefficient of a4
b8
, since 12
C8 = 12
C4

14. Example 2. In the expansion of (x − y)15
, calculate the coefficients of x3
y12
and x2
y13
.
15· 14· 13
1· 2· 3
= 455
.
The coefficient of x2
y13
, on the other hand, is negative, because the exponent of y is
odd. The coefficient is − 15
C13
= − 15
C2
. We have
−
15· 14
1· 2
= −10
5
Example 3. Write the 5th term in the expansion of (a + b)10.
Solution. In the 1st term, k = 0. In the 2nd term, k = 1. And so on. The index k of
each term is one less than the ordinal number of the term. Thus in the 5th term, k = 4.
The exponent of b is 4. The 5th term is
10
C4
a6
b4
=
10· 9· 8· 7
1· 2· 3· 4
a6
b4
= 210 a6
b4
Solution. The coefficient of x3y12 is positive, because the exponent of y is even.
That coefficient is 15C12. But 15C12 = 15C3, and so we have

15. Binomial Theorem for positive integral index
Any expression containing two terms only is called binomial expression eg. a+b, 1 + ab etc
For positive integer n
( )n n n 0 n n–1 1 n n–2 2 n 1 n–1 n 0 n
0 1 2 n–1 na b c a b c a b c a b ... c a b c a b+ = + + + + +
n
n n–r r
r
r 0
c a b
=
= ∑
where
( ) ( )
n n
r n–r
n! n!
c c for 0 r n
r! n – r ! n – r !r!
= = = ≤ ≤ are called binomial coefficients
( ) ( )n
r
n n – 1 ... n – r 1
C ,
1.2.3...r
+
= numerator contains r factors
10 10 10
7 10–7 3
10! 10.9.8
C 120 C C
7! 3! 3.2.1
= = = = =
Binomial theorem

16. Special cases of binomial theorem
( ) ( )n nn n n n–1 n n–2 2 n n
0 1 2 nx – y c x – c x y c x y ... –1 c y= + +
( )
n
r n n–r r
r
r 0
–1 c x y
=
= ∑
( )
n
n n n n 2 n n n r
0 1 2 n r
r 0
1 x c c x c x ... c x c x
=
+ = + + + + = ∑
in ascending powers of x
( )n n n n n–1 n
0 1 n1 x c x c x ... c+ = + + +
n
n n–r
r
r 0
c x
=
= ∑ ( )n
x 1= +
in descending powers of x

17. Solution :
Expand (x + y)4
+(x - y)4
and hence
find the value of ( ) ( )
4 4
2 1 2 1+ + −
( )4 4 4 0 4 3 1 4 2 2 4 1 3 4 0 4
0 1 2 3 4x y C x y C x y C x y C x y C x y+ = + + + +
4 3 2 2 3 4
x 4x y 6x y 4xy y= + + + +
Similarly ( )4 4 3 2 2 3 4
x y x 4x y 6x y 4xy y− = − + − +
( ) ( ) ( )4 4 4 2 2 4x y x y 2 x 6x y y∴ + + − = + +
( ) ( )
4 4 4 2 2 4Hence 2 1 2 1 2 2 6 2 1 1
 
+ + − = + + ÷
 
=34
Illustrative ExamplesIllustrative Examples

18. General term of (a + b)n
:
n n r r
r 1 rT c a b ,r 0,1,2,....,n−
+ = =
n n 0
1 0r 0, First Term T c a b= =
n n 1 1
2 1r 1, Second Term T c a b−= =
n n r 1 r 1
r r 1T c a b ,r 1,2,3,....,n− + −
−= =
1 2 3 4 5 n n 1
r 0 1 2 3 4 n 1 n
T T T T T T T +
= −
n+1 terms
kth term from end is (n-k+2)th term from beginning
Illustrative ExamplesIllustrative Examples

19. Solution : 9 r r
9
r 1 r
4x 5
T C
5 2x
−
+
−   
=  ÷  ÷
   
4 5 4 5
9
6 5 1 5 4 5
4x 5 9! 4 5
T T C
5 2x 4!5! 5 2 x
+
−   
= = = − ÷  ÷
   
39.8.7.6 2 .5
4.3.2.1 x
= − 5040
x
= −
Illustrative ExamplesIllustrative Examples
Find the 6th term in the
expansion of
and its 4th term from the end.
9
5
2x
 
− ÷
 
4x
5

20. 9 r r
9
r 1 r
4x 5
T C
5 2x
−
+
−   
=  ÷  ÷
   
4th term from end = 9-4+2 = 7th term from beginning i.e. T7
3 6 3 6
9
7 6 1 6 3 6 3
4x 5 9! 4 5
T T C
5 2x 3!6! 5 2 x
+
−   
= = = ÷  ÷
   
3
3
9.8.7 5
3.2.1 x
=
3
10500
x
=
Illustrative ExamplesIllustrative Examples

21. Middle term
Case I: n is even, i.e. number of terms odd only one middle term
th
n 2
term
2
+ 
 ÷
 
n n
n 2 2
n 2 n n
1
2 2 2
T T c a b+
+
= =
Case II: n is odd, i.e. number of terms even, two middle terms
th
n 1
term
2
+ 
 ÷
 
n 1 n 1
n 2 2
n 1 n 1 n 1
1
2 2 2
T T c a b
+ −
+ − −
+
= =
Middle term
= ?
2n
1
x
x
 
+ ÷
 
th
n 3
term
2
+ 
 ÷
 
n 1 n 1
n 2 2
n 3 n 1 n 1
1
2 2 2
T T c a b
− +
+ + +
+
= =
Illustrative ExamplesIllustrative Examples

22. Greatest Coefficient
CaseI: n even
n
1
2
n
term T is max i.e. for r
2+
=Coefficient of middle
n
n
2
C
CaseII: n odd
n 1 n 3
2 2
n 1 n 1
term T or T is max i.e. for r or
2 2
+ +
− +
=Coefficient of middle
n n
n 1 n 1
2 2
C or C− +
Illustrative ExamplesIllustrative Examples

23. Find the middle term(s) in the
expansion of
and hence find greatest coefficient
in the expansion
7
3x
3x
6
 
− ÷
 ÷
 
Solution :
Number of terms is 7 + 1 = 8 hence 2 middle terms, (7+1)/2 = 4th and (7+3)/2 = 5th
( )
3
3 4 13
47
4 3 1 3 3
x 7! 3 x
T T C 3x
6 4!3! 6
+
 −
= = = − ÷
 ÷
 
13
13
3
7.6.5 3x 105
x
3.2.1 82
= − = −
Illustrative ExamplesIllustrative Examples

24. Find the middle term(s) in the expansion
of and hence find greatest
coefficient in the expansion
7
3x
3x
6
 
− ÷
 ÷
 
( )
4
3 3 15
37
5 4 1 4 4
x 7! 3 x
T T C 3x
6 3!4! 6
+
 −
= = = ÷
 ÷
 
Solution :
15
15
4
7.6.5 x 35
x
3.2.1 482 3
= =
Hence Greatest coefficient is
7 7
4 3
7! 7.6.5
C or C or 35
3!4! 3.2.1
= =
Illustrative ExamplesIllustrative Examples

25. Find the coefficient of x5
in the expansion
of and term independent of x
10
2
3
1
3x
2x
 
− ÷
 
Solution :
( )
r10 r
10 2
r 1 r 3
1
T C 3x
2x
−
+
 
= − ÷
 
r
10 10 r 20 2r 3r
r
1
C 3 x
2
− − − 
= − ÷
 
For coefficient of x5 , 20 - 5r = 5 ⇒ r = 3
3
10 10 3 5
3 1 3
1
T C 3 x
2
−
+
 
= − ÷
 
Coefficient of x5
= -32805
Illustrative ExamplesIllustrative Examples

26. Solution Cont.
( )
r10 r
10 2
r 1 r 3
1
T C 3x
2x
−
+
 
= − ÷
 
r
10 10 r 20 2r 3r
r
1
C 3 x
2
− − − 
= − ÷
 
For term independent of x i.e. coefficient of x0 , 20 - 5r = 0 ⇒ r = 4
4
10 10 4
4 1 4
1
T C 3
2
−
+
 
= − ÷
 
Term independent of x
76545
8
=
Illustrative ExamplesIllustrative Examples

27. Find the term independent of
x in the expansion of
81 –1
3 5
1
x x .
2
 
 +
 
 
Solution :
8 r r
1 1
8 3 5
r 1 r
1
T C x . x
2
−
−
+
   
 ÷  ÷=
 ÷  ÷
   
8 r r8 r
8 3 5
r
1
C x
2
−− − 
=  ÷
 
40 5r 3r 40 8r8 r 8 r
8 815 15
r r
1 1
C x C x
2 2
− − −− −
   
= = ÷  ÷
   
For the term to be independent of x
40 8r
0 r 5
15
−
= ⇒ =
Hence sixth term is independent of x and is given by
3
8
6 5
1 8! 1
T C . 7
2 5! 3! 8
 
= = = ÷
 
6T 7=
Illustrative ExamplesIllustrative Examples

28. Find (i) the coefficient of x9
(ii) the term
independent of x, in the expansion
of
9
2 1
x
3x
 
− ÷
 
Solution :
( )
r9 r
9 2
r 1 r
1
T C x
3x
−
+
− 
=  ÷
 
r
9 18 2r r
r
1
C x
3
− −− 
=  ÷
 
r
9 18 3r
r
1
C x
3
−− 
=  ÷
 
i) For Coefficient of x9 , 18-3r = 9 ⇒ r = 3
3 3
9 9 9 9
4 r
1 9! 1 28
T C x x x
3 3! 6! 3 9
− − −   
= = = ÷  ÷
   
hence coefficient of x9 is -28/9
ii) Term independent of x or coefficient
of x0, 18 – 3r = 0 ⇒ r = 6
6 6
9
7 6
1 9! 1 28
T C
3 6! 3! 3 243
− −   
= = = ÷  ÷
   
Illustrative ExamplesIllustrative Examples