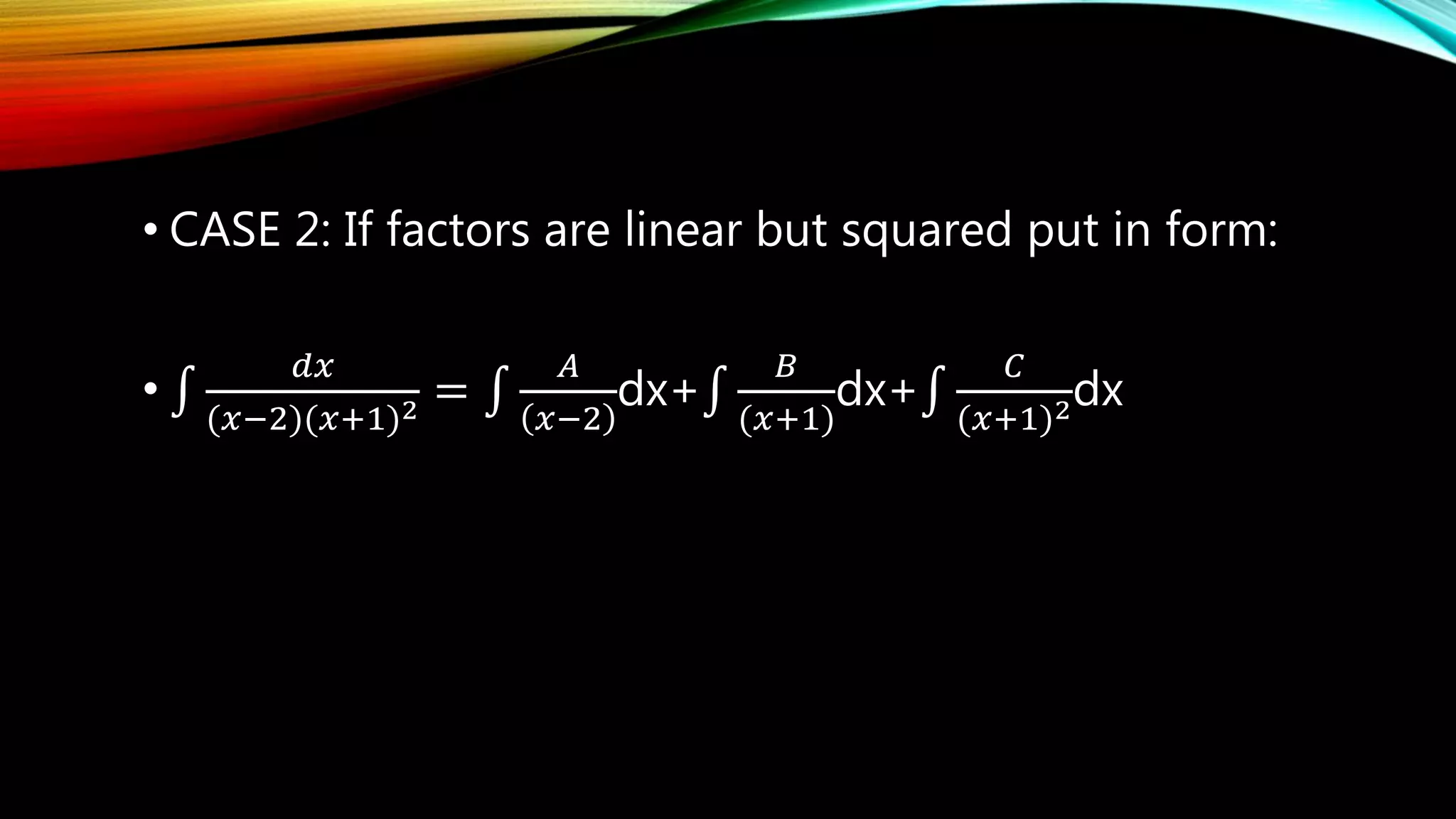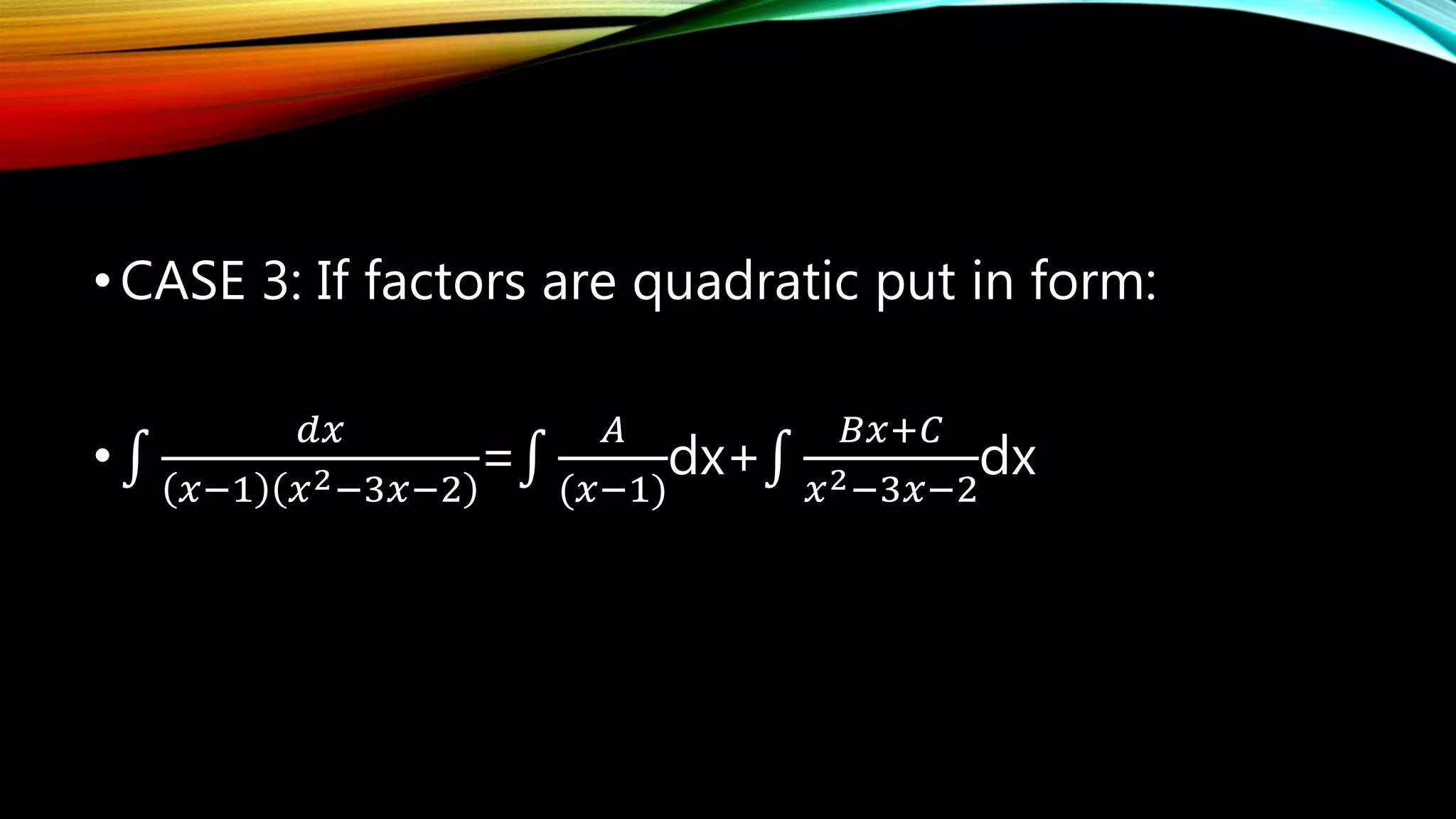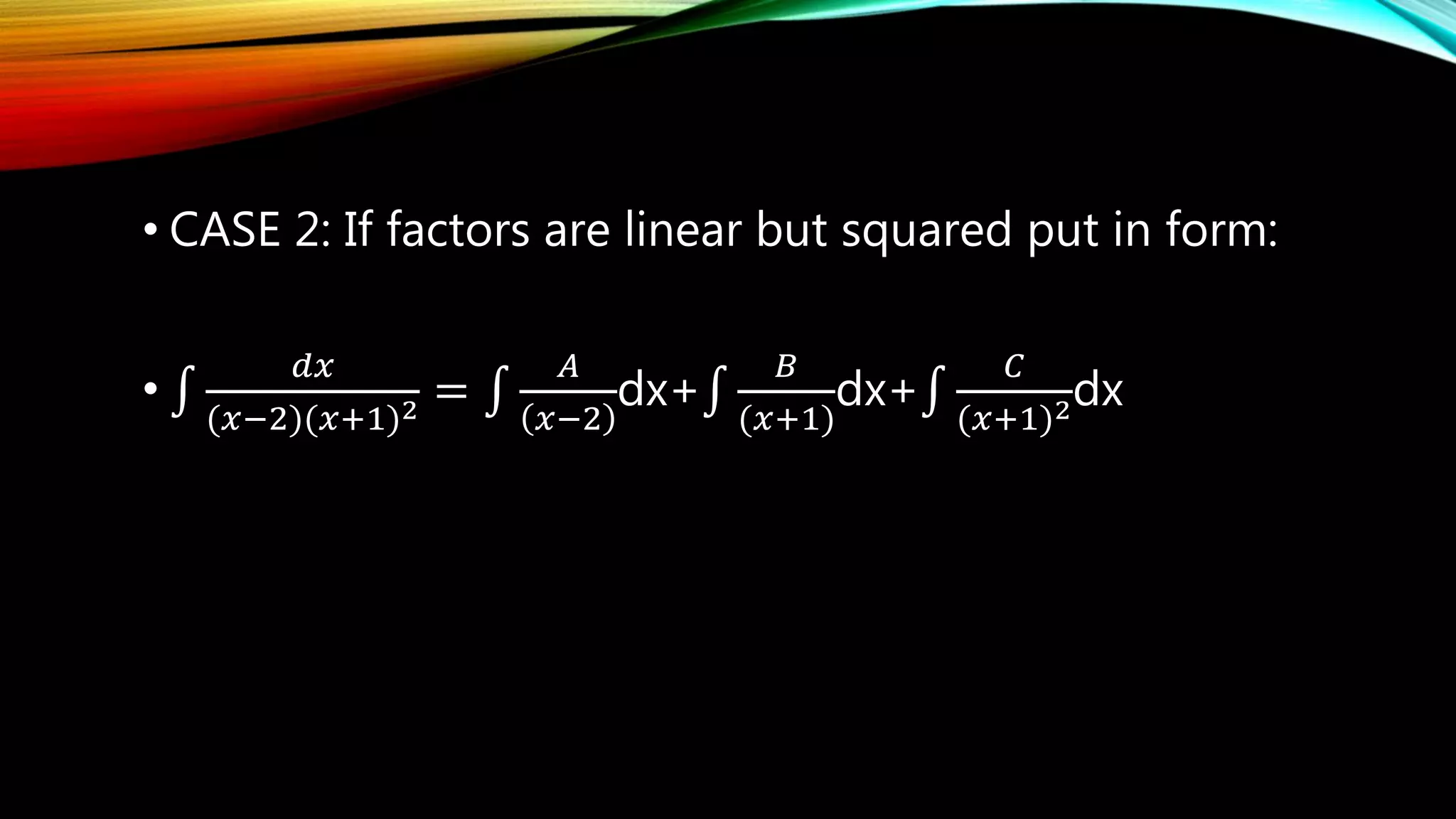
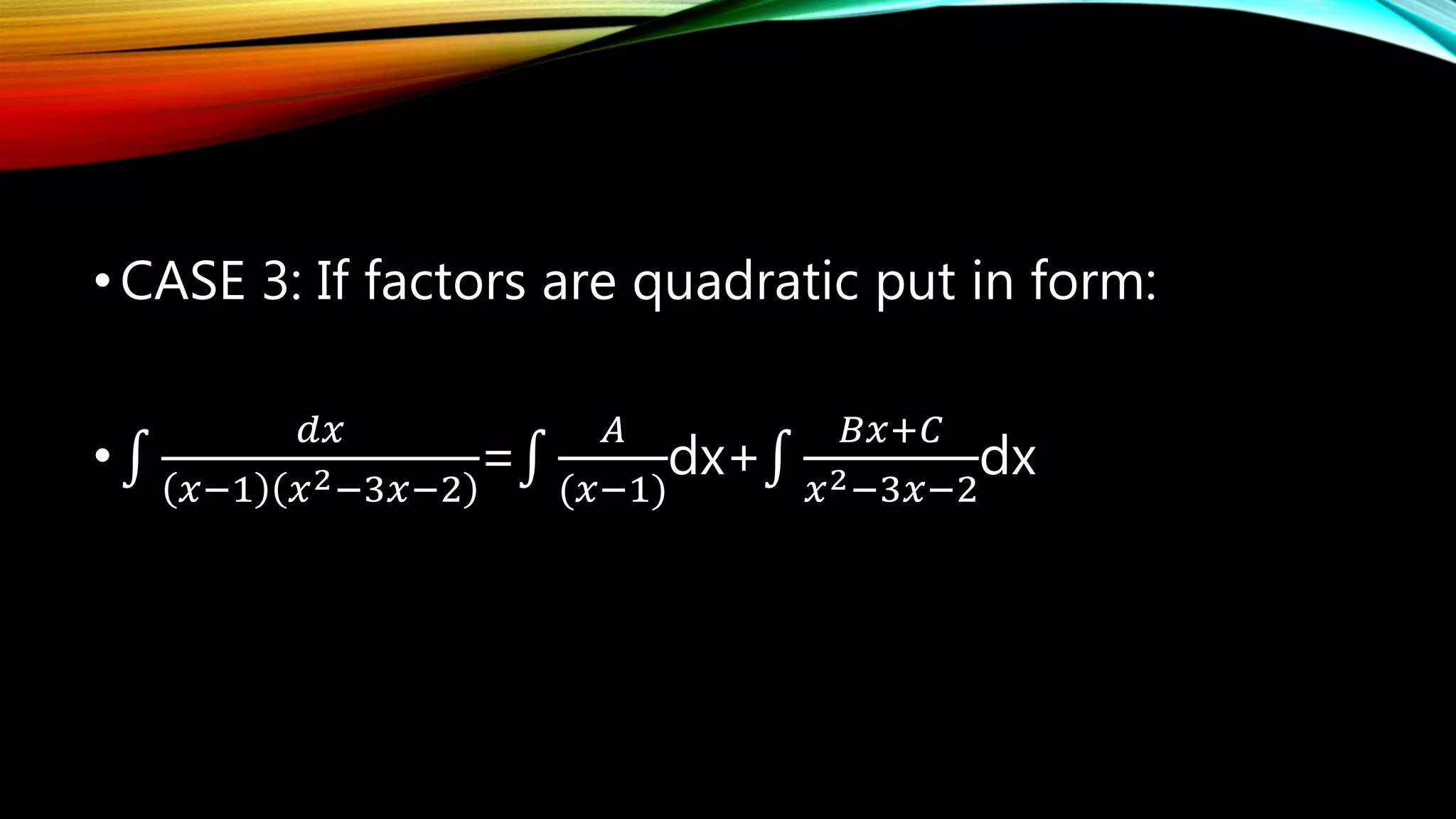
The document outlines the process of integration by partial fractions, describing various cases based on the types of factors in the denominator. It provides a series of steps to factorize denominators and solve integrals using different configurations depending on whether factors are linear or quadratic. An example is used to illustrate these steps, showing the solution for the integral of a specific rational function.

2. INTEGRATION BY PARTIAL
FRACTION:

4. • Step 1 Factorize denominator into irreducible factors
•
𝑥2
𝑥2−5𝑥+6
=
𝑑𝑥
(𝑥−3)(𝑥−2)
• CASE 1:If factors are linear put in form
𝐴
𝑥+𝑐
+
𝐵
𝑥+𝑑
and find A
and B
•
𝑑𝑥
𝑥−3 (𝑥−2)
=
𝐴
𝑥−3
ⅆ𝑥 +
𝐵
𝑋−2
ⅆ𝑥

5. • CASE 2: If factors are linear but squared put in form:
•
𝑑𝑥
(𝑥−2)(𝑥+1)2 =
𝐴
𝑥−2
dx+
𝐵
(𝑥+1)
dx+
𝐶
(𝑥+1)2dx

6. •CASE 3: If factors are quadratic put in form:
•
𝑑𝑥
𝑥−1 𝑥2−3𝑥−2
=
𝐴
(𝑥−1)
dx+
𝐵𝑥+𝐶
𝑥2−3𝑥−2
dx

7. •CASE 4: If factors are quadratics but squared put in
form:
•
𝑑𝑥
(𝑥−1)(𝑥2−3𝑥−2)2
•=
𝐴
(𝑥−1)
dx +
𝐵𝑥+𝐶
𝑥2−3𝑥−2
dx +
𝐷𝑥+𝐸
(𝑥2−3𝑥−2)2dx

9. EXAMPLE:
•
3𝑥+1
𝑥2−𝑥−6
ⅆ𝑥
•
3𝑥+1
𝑥2−𝑥−6
=
3𝑥+1
(𝑥+2)(𝑥−3)
• Let
3𝑥+1
(𝑥+2)(𝑥−3)
=
𝐴
(𝑥+2)
+
𝐵
(𝑥−3)
------eq 1
• Multiply by (𝑥 + 2)(𝑥 − 3) on both sides
• 3𝑥 + 1=A(x-3)+B(x-2) -------eq 2
• Factorization:
• 𝑥2 − 𝑥 − 6
• 𝑥2 − 3𝑥 + 2𝑥 − 6
• 𝑥 𝑥 − 3 + 2(𝑥 −
3)

10. • Put x-3 =0
• So x=3
• Put value of x in eq 2
• 3(3)+1=A(3-3)+ B (3+2)
• 10=5B
• B=2
• Put x+2=0
• So x=-2
• Put value of x in eq 2
• 3(-2)+1=A(-2-3)+ B(-2+2)
• -5=A(-5)
• A=1

11. • Put values of A and B in eq 1
•
3𝑥+1
(𝑥+2)(𝑥−3)
=
𝐴
(𝑥+2)
+
𝐵
(𝑥−3)
------eq 1
•
3𝑥+1
(𝑥+2)(𝑥−3)
=
1
𝑥+2
+
2
𝑥−3
• Now apply integration
•
3𝑥+1
(𝑥+2)(𝑥−3)
=
1
𝑥+2
ⅆ𝑥 + 2
1
𝑥−3
ⅆ𝑥
=2ln 𝑥 − 3 + ln 𝑥 + 2 +c
(here c is constant)

12. •THANKS FOR UR PRECIOUS
TIME…