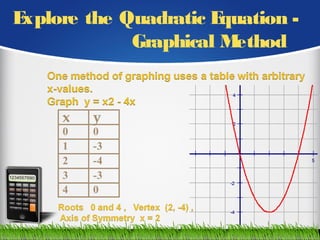
The document provides an extensive overview of solving quadratic equations, detailing various forms and methods including standard form, factoring, and the quadratic formula. It discusses the significance of coefficients a, b, and c, along with the discriminant's role in determining the nature of roots. Examples illustrate completing the square, factoring techniques, and graphical representation of quadratic functions.

1. Quadratic Equation
BY- Utkarsh Sharma

3. 2x2
+ 5x + 3 = 0 =
In this
one a=2, b=5 and c=3
x2
− 3x = 0
=
•This one is a little more tricky:
Where is a? Well a=1, and we don't
usually write "1x2
"
•b = -3
•And where is c? Well c=0, so is not
shown.
5x − 3 = 0
=
Oops! This one is not a quadratic
equation: it is missing x2
(in otherwords a=0, which means it
can't be quadratic)

4. So farwe have seen the "Standard Form" of a Quadratic Equation:
But sometimes a quadratic equation doesn't look like that..! Here are some
examples.. In disguise In Standard Form a, b and c
x2
= 3x -1 Move all terms to
left hand side
x2
- 3x + 1 = 0 a=1, b=-3, c=1
2(w2
- 2w) = 5 Expand (undo the
brackets), and
move 5 to left
2w2
- 4w - 5 = 0 a=2, b=-4, c=-5
z(z-1) = 3 Expand, and move
3 to left
z2
- z - 3 = 0
a=1, b=-1, c=-3
5 + 1/x - 1/x2
= 0 Multiply by x2
5x2
+ x - 1 = 0 a=5, b=1, c=-1

7. Factor
method……………
Step 1: Find two numbers that multiply to give ac, and
add to give b.
• Here .. a = 2 ,, …. b = 7…, c= 3
• ac is 2×3 = 6 and b is 7
• So we want two numbers that multiply together to make 6,
and add up to 7
• In fact 6 and 1 do that (6×1=6, and 6+1=7)
• How do we find 6 and 1?
• With the help of the factors of ac=6, and then try adding
some to get b=7.
• Factors of 6 include 1, 2, 3 and 6.
• Aha! 1 and 6 add to 7, and 6×1=6.

8. Step 2: Rewrite the middle with those numbers:
So we..............Rewrite 7x with 6x and 1x:
2x2
+ 6x + x + 3
Step 3: : Factor the first two and last two terms separately:
The first two terms 2x2
+ 6x factor into 2x(x+3)
The last two terms x+3 don't actually change in this case
So we get:
2x(x+3) + (x+3)
Step 4: If we've done this correctly, our two new terms should
have a clearly visible common factor.
In this case we can see that (x+3) is common to both terms
So we can now rewrite it like this:
2x(x+3) + (x+3) = (2x+1)(x+3) = 2x2
+7x + 3(hence it’s correct)

10. x2
+ bx + (b/2)2
=(x+b/2)2
In Algebra it looks like this:
by adding (b/2)2
we can complete the square. And
(x+b/2)2
has x only once, which is easier to use.

11. A Quadratic Equation looks like this:
And it can be solved using the Quadratic Formula:

13.  Move the numberterm to the right side of the equation: x2
+ 4x = -1
 Complete the square on the left side of the equation and balance this
by adding the same numberto the right side of the equation.
(b/2)2
= (4/2)2
= 22
= 4
x2
+ 4x + 4 = -1 + 4
(x + 2)2
= 3
Take the square root on both sides of the equation:
x + 2 = ±√3 = ±1.73
 Subtract 2 from both sides:
x = ±1.73 – 2 = -3.73 or-0.27

14. • A Quadratic Equationlooks like this:
And it can be solved using the Quadratic Formula:
The "±" means you need to do a plus AND a minus, so
there are normally TWO solutions !
The blue part (b2
- 4ac) is called the "discriminant“or ‘D’,
because it can "discriminate" between the possible types
of answer.
D = 0 , then root’s would be equal.
D > or = 0, Then root’s would be real.
D < 0 ,Then root’s would be unreal or imaginary or there
would be complex solutions .

16. • By using quadratic formula –
• Substitute a=6, b=5 and c=−6 into the formula:
• x = (−b ± √[b2
− 4ac]) / 2a
• x = (−5 ± √[52
− 4×6×(−6)]) / 2×6
• = (−5 ± √[25 + 144]) / 12
• = (−5 ± √169) / 12
• = (−5 ± 13) / 12
• So the two roots are:
• x = (-5 + 13) / 12 = 8/12 = 2/3,
• x = (-5 − 13) / 12 = −18/12 = −3/2

17. Explore the Quadratic Equation -
Graphical Method

18. Explore the Quadratic Equation -
Graphical Method
x x2
- 4 y
-3 (-3)2
- 4 5
-2 (-2)2
- 4 0
-1 (-1)2
- 4 -3
0 (0)2
- 4 -4
1 (1)2
- 4 -3
2 (2)2
- 4 0
3 (3)2
- 4 5

21. The height starts at 3 m: 3
It travels upwards at 14 meters per second (14 m/s): 14t
Gravity pulls it down, changing its speed by about 5 m/s per second (5 m/s2
):
−5t2
(Note for the enthusiastic: the -5t2
is simplified from -(½)at2
with a=9.81 m/s2
)

22. Multiply all terms by −1 to make it easier: 5t2
− 14t − 3 = 0
Now our job is to factor it.
We will use the "Find two numbers that multiply to give a×c, and add to
give b" method in Factoring Quadratics.
a×c = −15, and b = −14.
The positive factors of −15 are 1, 3, 5, 15, and one of the factors
has to be negative.
By trying a few combinations we find that −15 and 1 work
(−15×1 = −15, and −15+1 = −14)
Rewrite middle with -15 and 1: 5t2
− 15t + t − 3 = 0
Factor first two and last two: 5t(t − 3) + 1(t − 3) = 0
Common Factor is (t - 3): (5t + 1)(t − 3) = 0
And the two solutions are: 5t + 1 = 0 or t − 3 = 0
t = −0.2 or t = 3