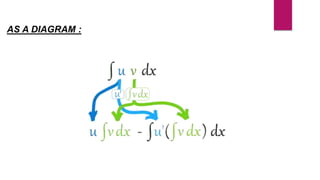
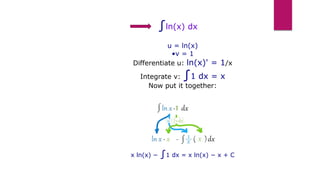The document discusses two methods for evaluating integrals: integration by substitution and integration by parts. Integration by substitution involves setting up an integral in a way that allows substituting a new variable u for an expression involving x, making the integral easier to evaluate. Integration by parts is a method for evaluating integrals of products of functions by breaking it into multiple integrals using the formula ∫u v dx = u∫v dx −∫u' (∫v dx) dx. The document provides examples of applying both methods to evaluate integrals of trigonometric, logarithmic, and exponential functions. It also briefly mentions partial fractions as a method to decompose rational functions into simpler fractions.

1. PRESENTATION
BY
MUHAMMAD TALHA

2. INTEGRATION BY SUBSITUTION
"
"Integration by Substitution" (also
called "u-Substitution" or "The
Reverse Chain Rule") is a method to
find an integral, but only when it can
be set up in a special way.

3. EXAMPLE NO 1 :
∫cos(x2) 2x dx
We know (from above) that it is in the right form
to do the substitution:
Now integrate:
∫cos(u) du = sin(u) + C
And finally put u=x2 back again:
sin(x2) + C

4. EXAMPLE NO 2 :
∫cos(x2) 6x dx
Oh no! It is 6x, not 2x like before. Our perfect
setup is gone.
Never fear! Just rearrange the integral like this:
∫cos(x2) 6x dx = 3∫cos(x2) 2x dx
Then go ahead as before:
3∫cos(u) du = 3 sin(u) + C
Now put u=x2 back again:
3 sin(x2) + C

5. EXAMPLE NO 03 :
Now let's try a slightly harder example:
∫x/(x2+1) dx
Let me see ... the derivative of x2+1 is 2x ... so how about we rearrange it like this
:
∫x/(x2+1) dx = ½∫2x/(x2+1) dx
Then we have:
Then integrate:
½∫1/u du = ½ ln(u) + C
Now put u=x2+1 back again:
½ ln(x2+1) + C

6. INTEGRATION BY PARTS
 INTEGRATION BY PART IS A METHOD
FOR EVALUATING THE DIFFERENT
INTEGRAL WHEN THE INTEGRAL IS A
PRODUCT OF FUNCTIONS, THE
INTEGRATION BY PARTS FORMULA
MOVE THE PRODUCT OUT OF THE
EQUALS SO THE INTEGRALS CAN
ALSO BE SOLVED MORE EASILY
 FORMULA :
ILATE
INVERSE
LOGRARITH
ALGEBRIC
TRIGNOMETRY
EXPONENTIAL
∫u v dx = u∫v dx −∫u' (∫v dx) dx

7. AS A DIAGRAM :

8. THERE ARE SOME EXAMPLES :
∫x cos(x) dx
u = x
v = cos(x)
So now it is in the format ∫u v dx we can proceed:
Differentiate u: u' = x' = 1
Integrate v: ∫v dx = ∫cos(x) dx = sin(x)
Now we can put it together:
x sin(x) − ∫sin(x) dx
x sin(x) + cos(x) + C
ANSWER

9. ∫ln(x) dx
u = ln(x)
•v = 1
Differentiate u: ln(x)' = 1/x
Integrate v: ∫1 dx = x
Now put it together:
x ln(x) − ∫1 dx = x ln(x) − x + C

10. ∫ex x dx
Choose u and v differently:
•u = x
•v = ex
Differentiate u: (x)' = 1
Integrate v: ∫ex dx = ex
Now put it together:
x ex − ex + C
ex(x−1) + C

11. PARTIAL FRACTION
 ONE OF THE SIMPLE FRACTIONS INTO THE SUM OF WHICH THE QUOTIENT OF
TWO POLYNOMILIALS MAY BE DECOMPOSED.
 FOR EXAMPLE
 5x+3/(x+3)(x+1)

12. THANK YOU…