Uploaded byKulsumPaleja1
PPTX, PDF52 views

derivatives part 1.pptx

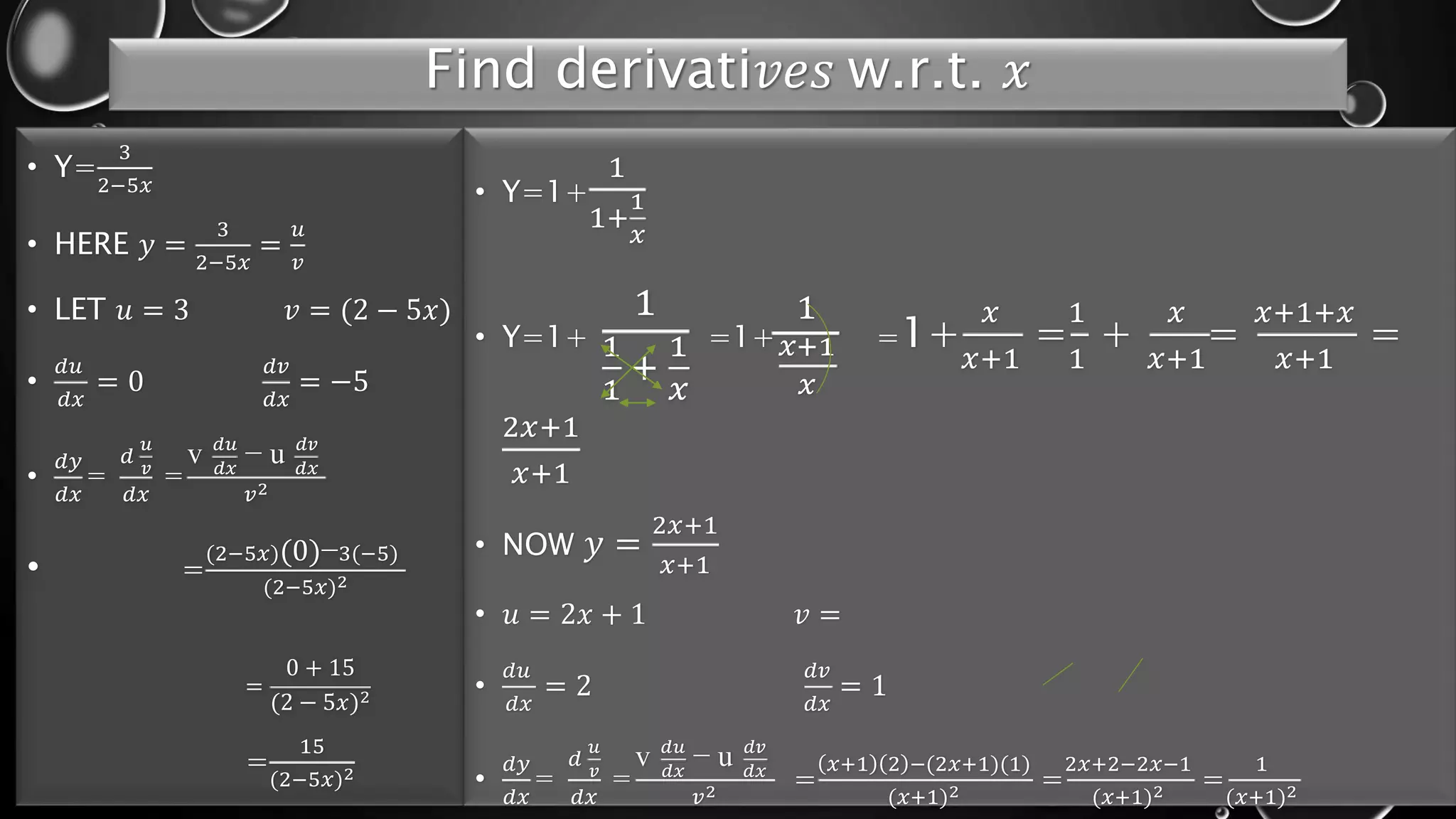
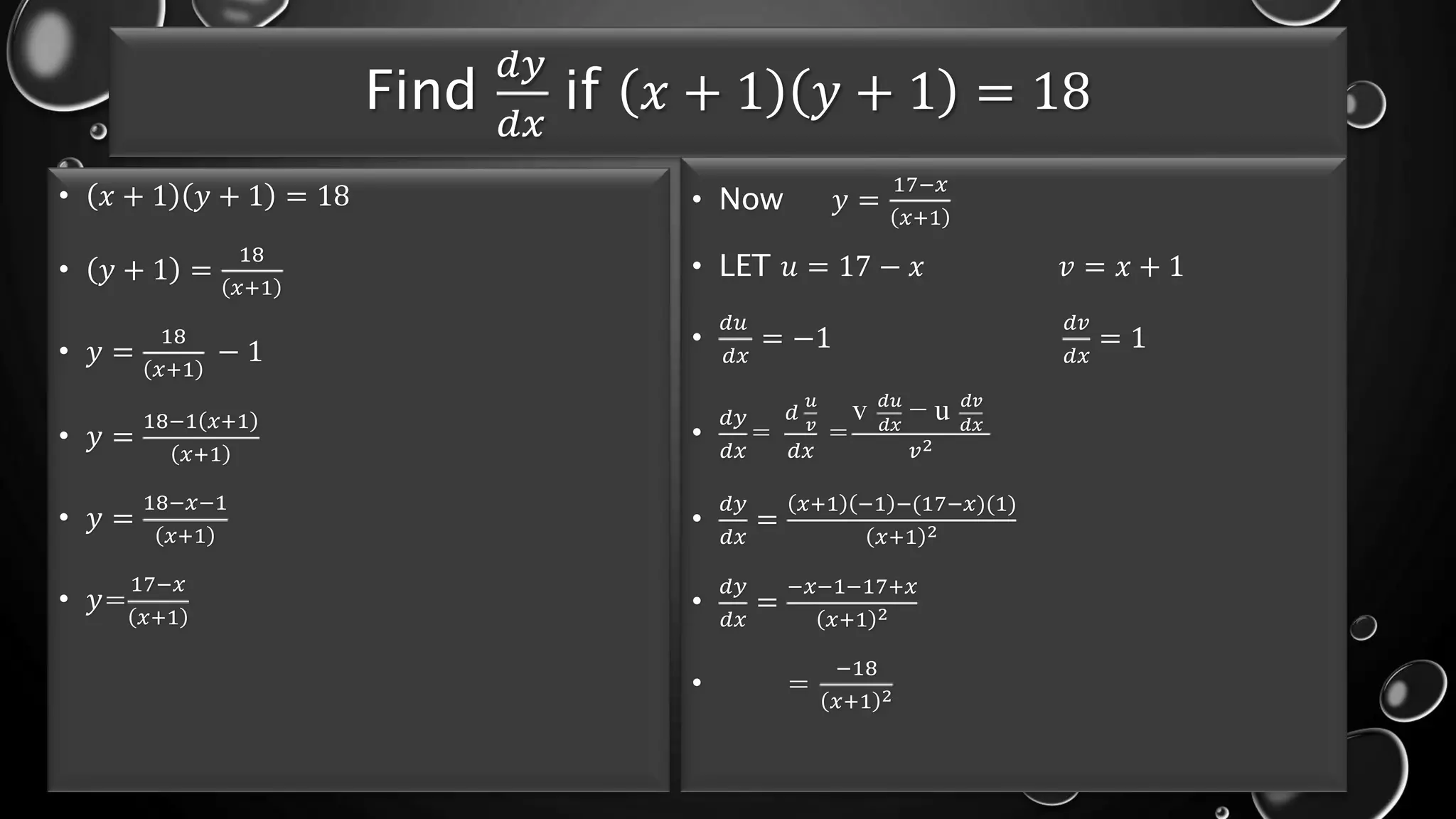
The document discusses derivatives and some rules for finding derivatives: - The derivative of a function f(x) is defined as the limit of the difference quotient as h approaches 0. - The derivative of a constant c is 0. - Important formulas are given for finding the derivatives of xn, x, ex, loge x, and other functions. - Rules are provided for finding the derivative of sums, differences, products, quotients, and composite functions using the chain rule. - Examples are worked out for finding the derivatives of various polynomial functions.

Embed presentation

Download to read offline
Derivatives WEIGHTAGE : 17 MARKS
USING DEFINITION OBTAIN DERIVATIVE • Find derivative of y = 𝒙 Here f(x)= 𝒙 Therefore f(x+h)= 𝒙 + 𝒉 Now according to definition of derivative • f’(x)= 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙+𝒉 −𝒇(𝒙) 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 𝒙+𝒉− 𝒙 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 𝒙+𝒉− 𝒙 𝒉 × 𝒙+𝒉+ 𝒙 𝒙+𝒉+ 𝒙 • = 𝐥𝐢𝐦 𝒉→𝟎 𝒙+𝒉 𝟐 − 𝒙 𝟐 𝒉( 𝒙+𝒉+ 𝒙) = lim ℎ→0 𝑥+ℎ−𝑥 ℎ ( 𝑥+ℎ+ 𝑥) = lim ℎ→0 ℎ ℎ ( 𝑥+ℎ+ 𝑥) = lim ℎ→0 1 ( 𝑥 + ℎ + 𝑥) = 1 ( 𝑥+0+ 𝑥) = 1 ( 𝑥 + 𝑥) = 1 2 𝑥
DERIVATIVE OF CONSTANT ( C ) • Find derivative of y =c Here f(x)=c Therefore f(x+h)=c Now according to definition of derivative • f’(x)= 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙+𝒉 −𝒇(𝒙) 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 𝒄−𝒄 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 𝟎 𝒉 • =0
Using definition find derivatives • Find derivative y=3𝑥2 − 2 Here f(x)= 3𝑥2 − 2 Therefore f(x+h)= 3 𝑥 + ℎ 2 − 2 =3(𝒙𝟐 +2xh+𝒉𝟐 )-2 = 3𝒙𝟐 +6xh+3𝒉𝟐 -2 Now according to definition of derivative • f’(x)= 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙+𝒉 −𝒇(𝒙) 𝒉 =𝐥𝐢𝐦 𝒉→𝟎 3𝒙𝟐+6xh+3𝒉𝟐−2 −(3𝑥2 −2) 𝒉 =𝐥𝐢𝐦 𝒉→𝟎 3𝒙𝟐+6xh+3𝒉𝟐−2−3𝑥2+𝟐 𝒉 • =𝐥𝐢𝐦 𝒉→𝟎 6xh+3𝒉𝟐 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 𝒉(6x+3𝒉) 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 (𝟔𝒙 + 𝒉) • = 𝟔𝒙 + 𝟎 • = 𝟔𝒙
Using definition find derivatives • Find derivative y=4𝑥2 + 5x − 2 Here f(x)= 4𝑥2 + 5x − 2 Therefore f(x+h)= 4 𝑥 + ℎ 2 + 5(x + h) − 2 =4(𝒙𝟐 +2xh+𝒉𝟐 ) + 𝟓(𝐱 + 𝐡)-2 = 4𝒙𝟐 +8xh+4𝒉𝟐 +5x+5h-2 Now according to definition of derivative • f’(x)= 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙+𝒉 −𝒇(𝒙) 𝒉 =𝐥𝐢𝐦 𝒉→𝟎 (4𝒙𝟐+8xh+4𝒉𝟐+5x+5h−2)−(4𝑥2+5x−2) 𝒉 =𝐥𝐢𝐦 𝒉→𝟎 4𝒙𝟐+8xh+4𝒉𝟐+5x+5h−2−4𝑥2−5x+2 𝒉 • =𝐥𝐢𝐦 𝒉→𝟎 8xh+4𝒉𝟐+5h 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 𝒉(8x+4h+5) 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 (8x+4h+5) • = 8𝒙 + 𝟒(𝟎) + 𝟓 • = 8𝒙+5
IMPORTANT FORMULAE FOR DIFFERENTIATION • If y = 𝑥𝑛 then 𝑑𝑦 𝑑𝑥 =n𝑥𝑛−1 • If y = x then 𝑑𝑦 𝑑𝑥 = 1 • If y=c then 𝑑𝑦 𝑑𝑥 =0 • If y=𝑒𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑒𝑥 • If y= 𝑎𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑎𝑥 loge a • If y= loge x then 𝑑𝑦 𝑑𝑥 = 1 𝑥
RULES OF DERIVATIVES • If U and V are functions of x then y=u+v then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢+𝑣) 𝑑𝑥 = 𝑑𝑢 𝑑𝑥 + 𝑑𝑣 𝑑𝑥 y=u−v then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢−𝑣) 𝑑𝑥 = 𝑑𝑢 𝑑𝑥 - 𝑑𝑣 𝑑𝑥 y=u×v then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢𝑣) 𝑑𝑥 = 𝑣 𝑑𝑢 𝑑𝑥 + u 𝑑𝑣 𝑑𝑥 Y=uvw then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢𝑣𝑤) 𝑑𝑥 = 𝑣𝑤 𝑑𝑢 𝑑𝑥 + 𝑢𝑤 𝑑𝑣 𝑑𝑥 + 𝑢𝑣 𝑑𝑤 𝑑𝑥 Y= 𝑢 𝑣 then 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 Chain rule : If y is function of u and u is function of x then 𝑑𝑦 𝑑𝑥 = 𝑑𝑦 𝑑𝑢 × 𝑑𝑢 𝑑𝑥
If U and V are functions of x then (I)y=u+v then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢+𝑣) 𝑑𝑥 = 𝑑𝑢 𝑑𝑥 + 𝑑𝑣 𝑑𝑥 (II)y=u−v then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢−𝑣) 𝑑𝑥 = 𝑑𝑢 𝑑𝑥 - 𝑑𝑣 𝑑𝑥 Find 𝑑𝑦 𝑑𝑥 of the following functions using rule (i) and (ii) (I) 3𝑥2 +2 SOLUTION : I. Y= 3𝑥2 +2 𝑑𝑦 𝑑𝑥 = 𝑑3𝑥2 𝑑𝑥 + 𝑑2 𝑑𝑥 [∵ RULE (I) APPLIED ] = 3(2X)+0 =6X (ii)4𝑥2 +5X+1 SOLUTION : Y= 4𝑥2 +5X+1 𝑑𝑦 𝑑𝑥 = 𝑑4𝑥2 𝑑𝑥 + 𝑑5𝑥 𝑑𝑥 + 𝑑1 𝑑𝑥 = 4(2X)+5(1) +0 = 8X+5 (III) 5X-9 SOLUTION : Y=5X-9 𝑑𝑦 𝑑𝑥 = 𝑑 5x 𝑑𝑥 - 𝑑9 𝑑𝑥 =5(1)-0 =5
Solve the following (i) y=𝑥3 + 𝑥2 + 𝑥 − 2 (II) y=7𝑥7 + 5𝑥4 − 20𝑥 + 37 • SOLUTION : • y=𝑥3 + 𝑥2 + 𝑥 − 2 • 𝑑𝑦 𝑑𝑥 = 𝑑𝑥3 𝑑𝑥 + 𝑑 𝑥2 𝑑𝑥 + 𝑑𝑥 𝑑𝑥 - 𝑑2 𝑑𝑥 • =(3𝑥3−1 ) +(2𝑥)+1-0 • = 3 𝑥2 +2𝑥+1 • SOLUTION: • y= 7𝑥7 + 5𝑥4 − 20𝑥 + 37 • 𝑑𝑦 𝑑𝑥 = 𝑑7𝑥7 𝑑𝑥 + 𝑑 5𝑥4 𝑑𝑥 - 𝑑20𝑥 𝑑𝑥 + 𝑑37 𝑑𝑥 • =7(7𝑥7−1 ) +5(4𝑥4−1 )- 20+0 • = 49𝑥6 +20𝑥3 − 20
(I) y=u×v then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢𝑣) 𝑑𝑥 = 𝑣 𝑑𝑢 𝑑𝑥 + u 𝑑𝑣 𝑑𝑥 II Y=uvw then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢𝑣𝑤) 𝑑𝑥 = 𝑣𝑤 𝑑𝑢 𝑑𝑥 + 𝑢𝑤 𝑑𝑣 𝑑𝑥 + 𝑢𝑣 𝑑𝑤 𝑑𝑥 • Find the derivative w.r.t 𝑥 • Y= (3𝑥2 − 2)(𝑥2 + 7) • 𝑢 = 3𝑥2 − 2 𝑣 = (𝑥2 + 7) • 𝑑𝑢 𝑑𝑥 =6𝑥 𝑑𝑣 𝑑𝑥 =2𝑥 • 𝑑𝑦 𝑑𝑥 = 𝑣 𝑑𝑢 𝑑𝑥 + u 𝑑𝑣 𝑑𝑥 • =(𝑥2 + 7)(6𝑥) + 3𝑥2 − 2 (2𝑥) • =(6𝑥3+42𝑥) +(6𝑥3-4𝑥) • = 6𝑥3 +42𝑥+ 6𝑥3 -4𝑥 • = 12𝑥3 +38𝑥 • Find the derivative w.r.t 𝑥 • Y= (2𝑥2 + 3)(3𝑥2 + 2)(𝑥+7) • 𝑢 = (2𝑥2 + 3) 𝑣 = 3𝑥2 + 2 𝑤 = (𝑥+7) • 𝑑𝑢 𝑑𝑥 = 4𝑥 + 0 𝑑𝑣 𝑑𝑥 = 6𝑥 + 0 𝑑𝑤 𝑑𝑥 = 1+0 • 𝑑𝑦 𝑑𝑥 = 𝑣𝑤 𝑑𝑢 𝑑𝑥 + 𝑢𝑤 𝑑𝑣 𝑑𝑥 + 𝑢𝑣 𝑑𝑤 𝑑𝑥 =(3𝑥2 + 2)(𝑥+7) 4𝑥+ (2𝑥2 + 3) (𝑥+7) 6𝑥+ (2𝑥2 + 3)(3𝑥2 + 2)1 = (3𝑥2 + 2)(4𝑥2+28𝑥)+ (2𝑥2 + 3)(6𝑥2+42𝑥) +(2𝑥2 + 3)(3𝑥2 + 2) = 4𝑥2 (3𝑥2 + 2)+ 28𝑥 (3𝑥2 + 2)+ 6𝑥2 (2𝑥2 + 3)+42𝑥(2𝑥2 + 3)+ 3𝑥2 (2𝑥2 + 3) + 2(2𝑥2 + 3) =12𝑥4 + 8𝑥2 + 84𝑥3 + 56𝑥 + 12𝑥4 + 18𝑥2 + 84𝑥3 + 126𝑥 + 6𝑥4 +9𝑥2 +4𝑥2 + 6 = 12𝑥4 + 12𝑥4 + 6𝑥4 +84𝑥3 +84𝑥3 + 8𝑥2 +18𝑥2 +9𝑥2 +4𝑥2 +56𝑥 + 126𝑥+6 =30𝑥4 + 168𝑥3 + 39𝑥2 + 182𝑥 + 6
NOW TRY YOUR SELF • FIND DERIVATIVES WITH RESPECT TO 𝑥 • Y=(2𝑥 + 3) 5𝑥3 − 2 • Y=𝑥4 + 𝑥5 + 5𝑥6 + 3𝑥2 + 3𝑥3 − 9 • Y=3𝑥4 + 13𝑥3 − 9𝑥 + 15 • Y=(𝑥 + 1)(9𝑥 + 5)(𝑥2 − 9) • Y= 3𝑥2 + 5𝑥 − 9 • Y=(𝑥2 + 𝑥 − 1)(𝑥2 + 𝑥 + 1) • Y=(2X-1)(6X+1) • Y=7𝑥2 + 123𝑥 − 100
Y= 𝑢 𝑣 then 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 • FIND THE DERIVATIVE OF 𝑦 = 1+𝑥 1+𝑥2 • HERE 𝑦 = 1+𝑥 1+𝑥2 = 𝑢 𝑣 • LET 𝑢 = (1 + 𝑥) 𝑣 = (1 + 𝑥2) • 𝑑𝑢 𝑑𝑥 = 0 + 1 𝑑𝑣 𝑑𝑥 = 0 + 2𝑥 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 • = (1+𝑥2) (1)−(1+𝑥)(2x) (1+𝑥2)2 = 1 + 𝑥2 − 2𝑥 − 2𝑥2 (1 + 𝑥2)2 = 1−2𝑥−𝑥2 (1+𝑥2)2 • FIND DERIVATIVE 𝑦 = 𝑥2+𝑥+1 𝑥2−𝑥+1 • HERE 𝑦 = 𝑥2+𝑥+1 𝑥2−𝑥+1 = 𝑢 𝑣 • LET 𝑢 = (𝑥2 + 𝑥 + 1) 𝑣 = (𝑥2 − 𝑥 + 1) • 𝑑𝑢 𝑑𝑥 = 2𝑥 + 1 𝑑𝑣 𝑑𝑥 = 2𝑥 − 1 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 • = (𝑥2−𝑥+1) (2X+1)−(𝑥2+𝑥+1)(2x−1) (1−𝑥+𝑥2)2 = =
Find derivati𝑣𝑒𝑠 w.r.t. 𝑥 • Y= 3 2−5𝑥 • HERE 𝑦 = 3 2−5𝑥 = 𝑢 𝑣 • LET 𝑢 = 3 𝑣 = (2 − 5𝑥) • 𝑑𝑢 𝑑𝑥 = 0 𝑑𝑣 𝑑𝑥 = −5 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 • = (2−5𝑥)(0)−3(−5) (2−5𝑥)2 = 0 + 15 (2 − 5𝑥)2 = 15 (2−5𝑥)2 • Y=1+ 1 1+ 1 𝑥 • Y=1+ 1 1 1 + 1 𝑥 =1+ 1 𝑥+1 𝑥 =1+ 𝑥 𝑥+1 = 1 1 + 𝑥 𝑥+1 = 𝑥+1+𝑥 𝑥+1 = 2𝑥+1 𝑥+1 • NOW 𝑦 = 2𝑥+1 𝑥+1 • 𝑢 = 2𝑥 + 1 𝑣 = • 𝑑𝑢 𝑑𝑥 = 2 𝑑𝑣 𝑑𝑥 = 1 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 = 𝑥+1 2 −(2𝑥+1)(1) (𝑥+1)2 = 2𝑥+2−2𝑥−1 (𝑥+1)2 = 1 (𝑥+1)2
Find derivative of 3 (𝑥+2)(𝑥+3) • 𝑦 = 3 (𝑥+2)(𝑥+3) • 𝑦 = 3 𝑥2+3𝑥+2𝑥+6 • ∴ 𝑦= 3 𝑥2+5𝑥+6 • NOW 𝑦 = 3 𝑥2+5𝑥+6 • 𝑢 = 3 𝑣 = 𝑥2 + 5𝑥 + 6 • 𝑑𝑢 𝑑𝑥 = 0 𝑑𝑣 𝑑𝑥 = 2𝑥 + 5 • 𝒅𝒚 𝒅𝒙 = 𝒅 𝒖 𝒗 𝒅𝒙 = v 𝒅𝒖 𝒅𝒙 − u 𝒅𝒗 𝒅𝒙 𝒗𝟐 • = (𝑥2+5𝑥+6)(0)−𝟑(𝟐𝒙+𝟓) (𝑥2+5𝑥+6)𝟐 • = −𝟑(𝟐𝒙+𝟓) (𝑥2+5𝑥+6)𝟐 • OR • = −𝟔𝒙−𝟏𝟓 (𝑥2+5𝑥+6)𝟐
(Find derivative of 𝑥 + 2𝑥+3 𝑥+2 𝑥 + 4𝑥+10 𝑥+3 • 𝑦 = 𝑥 + 2𝑥+3 𝑥+2 𝑥 + 4𝑥+10 𝑥+3 • 𝑦 = 𝑥 1 + 2𝑥+3 𝑥+2 𝑥 1 + 4𝑥+10 𝑥+3 • 𝑦 = 𝑥 𝑥+2 + 2𝑥+3 𝑥+2 𝑥 𝑥+3 + 4𝑥+10 𝑥+3 • 𝑦 = 𝑥2+2𝑥+2𝑥+3 𝑥+2 𝑥23𝑥+4𝑥+10 𝑥+3 • 𝑦 = 𝑥2+4𝑥+3 𝑥+2 𝑥2+7𝑥+10 𝑥+3 • 𝑦 = 𝑥2+3𝑥+𝑥+3 𝑥+2 𝑥2+5𝑥+2𝑥+10 𝑥+3 • 𝑦 = 𝑥 𝑥+3 +1(𝑥+3) 𝑥+2 𝑥 𝑥+5 +2(𝑥+5) (𝑥+3) • 𝑦 = 𝑥+1 𝑥+3 𝑥+2 𝑥+5 𝑥+2 𝑥+3 = 𝑥 + 1 𝑥 + 5 • 𝑦 = 𝑥 + 1 𝑥 + 5 • 𝑦 = 𝑥 𝑥 + 5 + 1 𝑥 + 5 • 𝑦 = 𝑥2 + 5𝑥 + 𝑥 + 5 • 𝑦 = 𝑥2 + 6𝑥 + 5 • NOW • 𝑑𝑦 𝑑𝑥 = 𝑑 (𝑥2+6𝑥+5) 𝑑𝑥 • 𝑑𝑦 𝑑𝑥 = 2𝑥 + 6
Find 𝑑𝑦 𝑑𝑥 if 𝑥 + 1 𝑦 + 1 = 18 • 𝑥 + 1 𝑦 + 1 = 18 • 𝑦 + 1 = 18 𝑥+1 • 𝑦 = 18 𝑥+1 − 1 • 𝑦 = 18−1 𝑥+1 𝑥+1 • 𝑦 = 18−𝑥−1 𝑥+1 • 𝑦= 17−𝑥 𝑥+1 • Now 𝑦 = 17−𝑥 𝑥+1 • LET 𝑢 = 17 − 𝑥 𝑣 = 𝑥 + 1 • 𝑑𝑢 𝑑𝑥 = −1 𝑑𝑣 𝑑𝑥 = 1 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 • 𝑑𝑦 𝑑𝑥 = 𝑥+1 −1 −(17−𝑥)(1) 𝑥+1 2 • 𝑑𝑦 𝑑𝑥 = −𝑥−1−17+𝑥 𝑥+1 2 • = −18 𝑥+1 2
F𝑖𝑛𝑑 𝑑𝑦 𝑑𝑥 𝑖𝑓 𝑥𝑦 + 𝑥 + 𝑦 − 2 = 0 • 𝑥𝑦 + 𝑥 + 𝑦 − 2 = 0 • 𝑥𝑦 + 𝑦 = 2 − 𝑥 • 𝑦 𝑥 + 1 = 2 − 𝑥 • 𝑦 = 2−𝑥 𝑥+1 • N𝑜𝑤 𝑦 = 2−𝑥 𝑥+1 • LET 𝑢 = 2 − 𝑥 𝑣 = 𝑥 + 1 • 𝑑𝑢 𝑑𝑥 = −1 𝑑𝑣 𝑑𝑥 = 1 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 • 𝑑𝑦 𝑑𝑥 = 𝑥+1 −1 −(2−𝑥)(1) 𝑥+1 2 • = −𝑥−1−2+𝑥 𝑥+1 2 • = −3 𝑥+1 2
𝐴𝑝𝑝𝑙𝑖𝑐𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒𝑠 • If y = 𝑥𝑛 then 𝑑𝑦 𝑑𝑥 =n𝑥𝑛−1 • If y = x then 𝑑𝑦 𝑑𝑥 = 1 • If y=c then 𝑑𝑦 𝑑𝑥 =0 • If y=𝑒𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑒𝑥 • If y= 𝑎𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑎𝑥 loge a • 𝐼𝑓𝑦 =loge x then 𝑑𝑦 𝑑𝑥 = 1 𝑥 • 𝐹𝑖𝑛𝑑 𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑥3 𝑒𝑥 𝑤𝑖𝑡ℎ 𝑟𝑒𝑠𝑝𝑒𝑐𝑡 𝑡𝑜 𝑥 𝐻𝑒𝑟𝑒 𝑦 = 𝑥3 𝑒𝑥 𝑢 = 𝑥2 𝑣 = 𝑒𝑥  𝑑𝑢 𝑑𝑥 = 2𝑥 𝑑𝑣 𝑑𝑥 = 𝑒𝑥  𝑑𝑦 𝑑𝑥 = 𝑣 𝑑𝑢 𝑑𝑥 + 𝑢 𝑑𝑣 𝑑𝑥 = (𝑒𝑥)(2𝑥)+(𝑥2)(𝑒𝑥) = 𝑥𝑒𝑥(2 + 𝑥)
𝐴𝑝𝑝𝑙𝑖𝑐𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒𝑠 • If y = 𝑥𝑛 then 𝑑𝑦 𝑑𝑥 =n𝑥𝑛−1 • If y = x then 𝑑𝑦 𝑑𝑥 = 1 • If y=c then 𝑑𝑦 𝑑𝑥 =0 • If y=𝑒𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑒𝑥 • If y= 𝑎𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑎𝑥 loge a • 𝐼𝑓𝑦 =loge x then 𝑑𝑦 𝑑𝑥 = 1 𝑥 • 𝑓𝑖𝑛𝑑 𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑥4 log 𝑥 • 𝐻𝑒𝑟𝑒 𝑦 = 𝑥4 log 𝑥 • 𝑢 = 𝑥4 𝑣 = 𝑙𝑜𝑔𝑥 • 𝑑𝑢 𝑑𝑥 = 4𝑥3 𝑑𝑣 𝑑𝑥 = 1 𝑥 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 = 𝑙𝑜𝑔𝑥 4𝑥3 − 𝑥4 1 𝑥 𝑙𝑜𝑔𝑥 2 = 𝑙𝑜𝑔𝑥 4𝑥3 − 𝑥3 𝑙𝑜𝑔𝑥 2 = 𝑥3 4𝑙𝑜𝑔𝑥−1 𝑙𝑜𝑔𝑥 2
𝐴𝑝𝑝𝑙𝑖𝑐𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒𝑠 • If y = 𝑥𝑛 then 𝑑𝑦 𝑑𝑥 =n𝑥𝑛−1 • If y = x then 𝑑𝑦 𝑑𝑥 = 1 • If y=c then 𝑑𝑦 𝑑𝑥 =0 • If y=𝑒𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑒𝑥 • If y= 𝑎𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑎𝑥 loge a • 𝐼𝑓𝑦 =loge x then 𝑑𝑦 𝑑𝑥 = 1 𝑥 • 𝐹𝑖𝑛𝑑 𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑥3/2 4𝑥 • 𝑢 = 𝑥3/2 𝑣 = 4𝑥 • 𝑑𝑢 𝑑𝑥 = 3 2 𝑥 3 2 −1 = 3 2 𝑥 1 2 𝑑𝑣 𝑑𝑥 = 4𝑥 log 4 • 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 = 𝑙𝑜𝑔𝑥 4𝑥3 − 𝑥4 1 𝑥 𝑙𝑜𝑔𝑥 2 = 𝑙𝑜𝑔𝑥 4𝑥3 − 𝑥3 𝑙𝑜𝑔𝑥 2 = 𝑥3 4𝑙𝑜𝑔𝑥−1 𝑙𝑜𝑔𝑥 2
𝐴𝑝𝑝𝑙𝑖𝑐𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒𝑠 • If y = 𝑥𝑛 then 𝑑𝑦 𝑑𝑥 =n𝑥𝑛−1 • If y = x then 𝑑𝑦 𝑑𝑥 = 1 • If y=c then 𝑑𝑦 𝑑𝑥 =0 • If y=𝑒𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑒𝑥 • If y= 𝑎𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑎𝑥 loge a • 𝐼𝑓𝑦 =loge x then 𝑑𝑦 𝑑𝑥 = 1 𝑥

More Related Content

PPTX
presentation on differentiaton 1.pptm.pptx
byks10151727
 
PPTX
DERIVATIVES implicit function.pptx
byKulsumPaleja1
 
PDF
Difrentiation 140930015134-phpapp01
byrakambantah
 
PPTX
Differential Calculus- differentiation
bySanthanam Krishnan
 
PPTX
DIFFERENTAL CALCULUS DERIVATIVES FIRST PART
byteacherlablidas
 
PDF
College textbook business math and statistics - section b - business mathem...
byPraveen Tyagi
 
PPTX
Integral and Differential CalculusI.pptx
byJhennyRosePahed1
 
PDF
Difrentiation
bylecturer
 
presentation on differentiaton 1.pptm.pptx
byks10151727
 
DERIVATIVES implicit function.pptx
byKulsumPaleja1
 
Difrentiation 140930015134-phpapp01
byrakambantah
 
Differential Calculus- differentiation
bySanthanam Krishnan
 
DIFFERENTAL CALCULUS DERIVATIVES FIRST PART
byteacherlablidas
 
College textbook business math and statistics - section b - business mathem...
byPraveen Tyagi
 
Integral and Differential CalculusI.pptx
byJhennyRosePahed1
 
Difrentiation
bylecturer
 

Similar to derivatives part 1.pptx

PPTX
Basic Mathematics
byAdeel Iftikhar
 
PPTX
Antiderivatives: Power, Sum and Difference
byRivenBarquilla
 
PDF
2020-rules-of-differentiation-sinhala.pdf
bysithumMarasighe
 
PDF
Math refresher
bydelilahnan
 
PDF
Differential Calculus
byOlooPundit
 
DOC
Chapter 4(differentiation)
byEko Wijayanto
 
PDF
Basic Calculus (Module 9) - Intermediate Value Theorem
bychrishelyndacsil2
 
PPT
P9 products
bywalshbarbaram
 
PPTX
derivative -I for higher classes bca and bba
byKulsumPaleja1
 
PDF
MATH&151 Final Project Fundamentals of Derivatives.pdf
byjustchris20077
 
PDF
3. DERIVATIVE BY INCREMENT IN CALULUS 01
byoliverosmarcial24
 
PDF
exponen dan logaritma
byHanifa Zulfitri
 
PPTX
1-Basic Rules of Differddddentiation.pptx
bydominicdaltoncaling2
 
DOCX
BSC_COMPUTER _SCIENCE_UNIT-1_DISCRETE MATHEMATICS
byRai University
 
DOCX
BSC_Computer Science_Discrete Mathematics_Unit-I
byRai University
 
PDF
Cuaderno de trabajo derivadas experiencia 1
byMariamne3
 
PPTX
Derivatives
bygregorblanco
 
PPTX
Rules of derivative
byjameel shigri
 
PDF
Lesson 1 Nov 12 09
byingroy
 
PPTX
Calculus revision card
byPuna Ripiye
 
Basic Mathematics
byAdeel Iftikhar
 
Antiderivatives: Power, Sum and Difference
byRivenBarquilla
 
2020-rules-of-differentiation-sinhala.pdf
bysithumMarasighe
 
Math refresher
bydelilahnan
 
Differential Calculus
byOlooPundit
 
Chapter 4(differentiation)
byEko Wijayanto
 
Basic Calculus (Module 9) - Intermediate Value Theorem
bychrishelyndacsil2
 
P9 products
bywalshbarbaram
 
derivative -I for higher classes bca and bba
byKulsumPaleja1
 
MATH&151 Final Project Fundamentals of Derivatives.pdf
byjustchris20077
 
3. DERIVATIVE BY INCREMENT IN CALULUS 01
byoliverosmarcial24
 
exponen dan logaritma
byHanifa Zulfitri
 
1-Basic Rules of Differddddentiation.pptx
bydominicdaltoncaling2
 
BSC_COMPUTER _SCIENCE_UNIT-1_DISCRETE MATHEMATICS
byRai University
 
BSC_Computer Science_Discrete Mathematics_Unit-I
byRai University
 
Cuaderno de trabajo derivadas experiencia 1
byMariamne3
 
Derivatives
bygregorblanco
 
Rules of derivative
byjameel shigri
 
Lesson 1 Nov 12 09
byingroy
 
Calculus revision card
byPuna Ripiye
 

Recently uploaded

PPTX
AN EXTREMELY BORING GENERAL QUIZ FOR UG.pptx
bySriramG47
 
PPTX
Partial Correlation of Coefficient - Values of r₁₂.₃, r₂₃.₁ & r₁₃.₂
bySundar B N
 
PPTX
How to Configure Push & Pull Rule in Odoo 18 Inventory
byCeline George
 
PPTX
UNIT 1: COMMUNICATION SKILLS, BARRIERS TO COMMUNICATION, PERSPECTIVES IN COMM...
byPOOJA KARVANDE
 
PPTX
META-ANALYSIS INTERPRETATION, PUBLICATION BIAS AND GRADE ASSESSMENT.pptx
bySystematic Reviews Network (SRN)
 
PPTX
Accounting Skills Paper-II (Registers of PACs and Credit Co-operative Societies)
byDr. Sushil Bansode
 
PPTX
Nursing Unit Management, patient care unit, physical layout of nursing unit,t...
byyellow4878
 
PDF
Micro Economics for class 12 and class 11
bysurajbajaj4116
 
PPTX
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
PPTX
Multiple Linear Regression - Least Square Method X₁ on X₂ and X₃
bySundar B N
 
PDF
Multiple Myeloma , definition, etiology, PP, CM , DE and management
byNisha Borsa
 
PDF
IMANI Africa files RTI request seeking full disclosure on 2026 SIM registrati...
bynservice241
 
PDF
International Men's Day Event: Breaking the Silence: Embracing Vulnerability ...
byAssociation for Project Management
 
PDF
Blood Group Incompatibility: Rh Factor and Erythroblastosis Fetalis
bySudhandraKarthi
 
PDF
Scalable-MADDPG-Based Cooperative Target Invasion for a Multi-USV System.pdf
byMan_Ebook
 
PDF
Analyzing the data of your initial survey
byThelma Villaflores
 
PPTX
Expected Revenue Report In Odoo 18 CRM
byCeline George
 
PPTX
The Cell & Cell Cycle-detailed structure and function of organelles.pptx
byAshish Umale
 
PDF
Cultivating Greatness Pune's Best Preschools and Schools.pdf
byWellington College
 
PDF
Risk management in Moroccan public hospitals_ a literature review
byMan_Ebook
 
AN EXTREMELY BORING GENERAL QUIZ FOR UG.pptx
bySriramG47
 
Partial Correlation of Coefficient - Values of r₁₂.₃, r₂₃.₁ & r₁₃.₂
bySundar B N
 
How to Configure Push & Pull Rule in Odoo 18 Inventory
byCeline George
 
UNIT 1: COMMUNICATION SKILLS, BARRIERS TO COMMUNICATION, PERSPECTIVES IN COMM...
byPOOJA KARVANDE
 
META-ANALYSIS INTERPRETATION, PUBLICATION BIAS AND GRADE ASSESSMENT.pptx
bySystematic Reviews Network (SRN)
 
Accounting Skills Paper-II (Registers of PACs and Credit Co-operative Societies)
byDr. Sushil Bansode
 
Nursing Unit Management, patient care unit, physical layout of nursing unit,t...
byyellow4878
 
Micro Economics for class 12 and class 11
bysurajbajaj4116
 
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
Multiple Linear Regression - Least Square Method X₁ on X₂ and X₃
bySundar B N
 
Multiple Myeloma , definition, etiology, PP, CM , DE and management
byNisha Borsa
 
IMANI Africa files RTI request seeking full disclosure on 2026 SIM registrati...
bynservice241
 
International Men's Day Event: Breaking the Silence: Embracing Vulnerability ...
byAssociation for Project Management
 
Blood Group Incompatibility: Rh Factor and Erythroblastosis Fetalis
bySudhandraKarthi
 
Scalable-MADDPG-Based Cooperative Target Invasion for a Multi-USV System.pdf
byMan_Ebook
 
Analyzing the data of your initial survey
byThelma Villaflores
 
Expected Revenue Report In Odoo 18 CRM
byCeline George
 
The Cell & Cell Cycle-detailed structure and function of organelles.pptx
byAshish Umale
 
Cultivating Greatness Pune's Best Preschools and Schools.pdf
byWellington College
 
Risk management in Moroccan public hospitals_ a literature review
byMan_Ebook
 

derivatives part 1.pptx

  • 1.
  • 2.
    USING DEFINITION OBTAINDERIVATIVE • Find derivative of y = 𝒙 Here f(x)= 𝒙 Therefore f(x+h)= 𝒙 + 𝒉 Now according to definition of derivative • f’(x)= 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙+𝒉 −𝒇(𝒙) 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 𝒙+𝒉− 𝒙 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 𝒙+𝒉− 𝒙 𝒉 × 𝒙+𝒉+ 𝒙 𝒙+𝒉+ 𝒙 • = 𝐥𝐢𝐦 𝒉→𝟎 𝒙+𝒉 𝟐 − 𝒙 𝟐 𝒉( 𝒙+𝒉+ 𝒙) = lim ℎ→0 𝑥+ℎ−𝑥 ℎ ( 𝑥+ℎ+ 𝑥) = lim ℎ→0 ℎ ℎ ( 𝑥+ℎ+ 𝑥) = lim ℎ→0 1 ( 𝑥 + ℎ + 𝑥) = 1 ( 𝑥+0+ 𝑥) = 1 ( 𝑥 + 𝑥) = 1 2 𝑥
  • 3.
    DERIVATIVE OF CONSTANT( C ) • Find derivative of y =c Here f(x)=c Therefore f(x+h)=c Now according to definition of derivative • f’(x)= 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙+𝒉 −𝒇(𝒙) 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 𝒄−𝒄 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 𝟎 𝒉 • =0
  • 4.
    Using definition findderivatives • Find derivative y=3𝑥2 − 2 Here f(x)= 3𝑥2 − 2 Therefore f(x+h)= 3 𝑥 + ℎ 2 − 2 =3(𝒙𝟐 +2xh+𝒉𝟐 )-2 = 3𝒙𝟐 +6xh+3𝒉𝟐 -2 Now according to definition of derivative • f’(x)= 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙+𝒉 −𝒇(𝒙) 𝒉 =𝐥𝐢𝐦 𝒉→𝟎 3𝒙𝟐+6xh+3𝒉𝟐−2 −(3𝑥2 −2) 𝒉 =𝐥𝐢𝐦 𝒉→𝟎 3𝒙𝟐+6xh+3𝒉𝟐−2−3𝑥2+𝟐 𝒉 • =𝐥𝐢𝐦 𝒉→𝟎 6xh+3𝒉𝟐 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 𝒉(6x+3𝒉) 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 (𝟔𝒙 + 𝒉) • = 𝟔𝒙 + 𝟎 • = 𝟔𝒙
  • 5.
    Using definition findderivatives • Find derivative y=4𝑥2 + 5x − 2 Here f(x)= 4𝑥2 + 5x − 2 Therefore f(x+h)= 4 𝑥 + ℎ 2 + 5(x + h) − 2 =4(𝒙𝟐 +2xh+𝒉𝟐 ) + 𝟓(𝐱 + 𝐡)-2 = 4𝒙𝟐 +8xh+4𝒉𝟐 +5x+5h-2 Now according to definition of derivative • f’(x)= 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙+𝒉 −𝒇(𝒙) 𝒉 =𝐥𝐢𝐦 𝒉→𝟎 (4𝒙𝟐+8xh+4𝒉𝟐+5x+5h−2)−(4𝑥2+5x−2) 𝒉 =𝐥𝐢𝐦 𝒉→𝟎 4𝒙𝟐+8xh+4𝒉𝟐+5x+5h−2−4𝑥2−5x+2 𝒉 • =𝐥𝐢𝐦 𝒉→𝟎 8xh+4𝒉𝟐+5h 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 𝒉(8x+4h+5) 𝒉 • = 𝐥𝐢𝐦 𝒉→𝟎 (8x+4h+5) • = 8𝒙 + 𝟒(𝟎) + 𝟓 • = 8𝒙+5
  • 6.
    IMPORTANT FORMULAE FOR DIFFERENTIATION •If y = 𝑥𝑛 then 𝑑𝑦 𝑑𝑥 =n𝑥𝑛−1 • If y = x then 𝑑𝑦 𝑑𝑥 = 1 • If y=c then 𝑑𝑦 𝑑𝑥 =0 • If y=𝑒𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑒𝑥 • If y= 𝑎𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑎𝑥 loge a • If y= loge x then 𝑑𝑦 𝑑𝑥 = 1 𝑥
  • 7.
    RULES OF DERIVATIVES •If U and V are functions of x then y=u+v then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢+𝑣) 𝑑𝑥 = 𝑑𝑢 𝑑𝑥 + 𝑑𝑣 𝑑𝑥 y=u−v then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢−𝑣) 𝑑𝑥 = 𝑑𝑢 𝑑𝑥 - 𝑑𝑣 𝑑𝑥 y=u×v then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢𝑣) 𝑑𝑥 = 𝑣 𝑑𝑢 𝑑𝑥 + u 𝑑𝑣 𝑑𝑥 Y=uvw then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢𝑣𝑤) 𝑑𝑥 = 𝑣𝑤 𝑑𝑢 𝑑𝑥 + 𝑢𝑤 𝑑𝑣 𝑑𝑥 + 𝑢𝑣 𝑑𝑤 𝑑𝑥 Y= 𝑢 𝑣 then 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 Chain rule : If y is function of u and u is function of x then 𝑑𝑦 𝑑𝑥 = 𝑑𝑦 𝑑𝑢 × 𝑑𝑢 𝑑𝑥
  • 8.
    If U andV are functions of x then (I)y=u+v then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢+𝑣) 𝑑𝑥 = 𝑑𝑢 𝑑𝑥 + 𝑑𝑣 𝑑𝑥 (II)y=u−v then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢−𝑣) 𝑑𝑥 = 𝑑𝑢 𝑑𝑥 - 𝑑𝑣 𝑑𝑥 Find 𝑑𝑦 𝑑𝑥 of the following functions using rule (i) and (ii) (I) 3𝑥2 +2 SOLUTION : I. Y= 3𝑥2 +2 𝑑𝑦 𝑑𝑥 = 𝑑3𝑥2 𝑑𝑥 + 𝑑2 𝑑𝑥 [∵ RULE (I) APPLIED ] = 3(2X)+0 =6X (ii)4𝑥2 +5X+1 SOLUTION : Y= 4𝑥2 +5X+1 𝑑𝑦 𝑑𝑥 = 𝑑4𝑥2 𝑑𝑥 + 𝑑5𝑥 𝑑𝑥 + 𝑑1 𝑑𝑥 = 4(2X)+5(1) +0 = 8X+5 (III) 5X-9 SOLUTION : Y=5X-9 𝑑𝑦 𝑑𝑥 = 𝑑 5x 𝑑𝑥 - 𝑑9 𝑑𝑥 =5(1)-0 =5
  • 9.
    Solve the following (i)y=𝑥3 + 𝑥2 + 𝑥 − 2 (II) y=7𝑥7 + 5𝑥4 − 20𝑥 + 37 • SOLUTION : • y=𝑥3 + 𝑥2 + 𝑥 − 2 • 𝑑𝑦 𝑑𝑥 = 𝑑𝑥3 𝑑𝑥 + 𝑑 𝑥2 𝑑𝑥 + 𝑑𝑥 𝑑𝑥 - 𝑑2 𝑑𝑥 • =(3𝑥3−1 ) +(2𝑥)+1-0 • = 3 𝑥2 +2𝑥+1 • SOLUTION: • y= 7𝑥7 + 5𝑥4 − 20𝑥 + 37 • 𝑑𝑦 𝑑𝑥 = 𝑑7𝑥7 𝑑𝑥 + 𝑑 5𝑥4 𝑑𝑥 - 𝑑20𝑥 𝑑𝑥 + 𝑑37 𝑑𝑥 • =7(7𝑥7−1 ) +5(4𝑥4−1 )- 20+0 • = 49𝑥6 +20𝑥3 − 20
  • 10.
    (I) y=u×v then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢𝑣) 𝑑𝑥 =𝑣 𝑑𝑢 𝑑𝑥 + u 𝑑𝑣 𝑑𝑥 II Y=uvw then 𝑑𝑦 𝑑𝑥 = 𝑑(𝑢𝑣𝑤) 𝑑𝑥 = 𝑣𝑤 𝑑𝑢 𝑑𝑥 + 𝑢𝑤 𝑑𝑣 𝑑𝑥 + 𝑢𝑣 𝑑𝑤 𝑑𝑥 • Find the derivative w.r.t 𝑥 • Y= (3𝑥2 − 2)(𝑥2 + 7) • 𝑢 = 3𝑥2 − 2 𝑣 = (𝑥2 + 7) • 𝑑𝑢 𝑑𝑥 =6𝑥 𝑑𝑣 𝑑𝑥 =2𝑥 • 𝑑𝑦 𝑑𝑥 = 𝑣 𝑑𝑢 𝑑𝑥 + u 𝑑𝑣 𝑑𝑥 • =(𝑥2 + 7)(6𝑥) + 3𝑥2 − 2 (2𝑥) • =(6𝑥3+42𝑥) +(6𝑥3-4𝑥) • = 6𝑥3 +42𝑥+ 6𝑥3 -4𝑥 • = 12𝑥3 +38𝑥 • Find the derivative w.r.t 𝑥 • Y= (2𝑥2 + 3)(3𝑥2 + 2)(𝑥+7) • 𝑢 = (2𝑥2 + 3) 𝑣 = 3𝑥2 + 2 𝑤 = (𝑥+7) • 𝑑𝑢 𝑑𝑥 = 4𝑥 + 0 𝑑𝑣 𝑑𝑥 = 6𝑥 + 0 𝑑𝑤 𝑑𝑥 = 1+0 • 𝑑𝑦 𝑑𝑥 = 𝑣𝑤 𝑑𝑢 𝑑𝑥 + 𝑢𝑤 𝑑𝑣 𝑑𝑥 + 𝑢𝑣 𝑑𝑤 𝑑𝑥 =(3𝑥2 + 2)(𝑥+7) 4𝑥+ (2𝑥2 + 3) (𝑥+7) 6𝑥+ (2𝑥2 + 3)(3𝑥2 + 2)1 = (3𝑥2 + 2)(4𝑥2+28𝑥)+ (2𝑥2 + 3)(6𝑥2+42𝑥) +(2𝑥2 + 3)(3𝑥2 + 2) = 4𝑥2 (3𝑥2 + 2)+ 28𝑥 (3𝑥2 + 2)+ 6𝑥2 (2𝑥2 + 3)+42𝑥(2𝑥2 + 3)+ 3𝑥2 (2𝑥2 + 3) + 2(2𝑥2 + 3) =12𝑥4 + 8𝑥2 + 84𝑥3 + 56𝑥 + 12𝑥4 + 18𝑥2 + 84𝑥3 + 126𝑥 + 6𝑥4 +9𝑥2 +4𝑥2 + 6 = 12𝑥4 + 12𝑥4 + 6𝑥4 +84𝑥3 +84𝑥3 + 8𝑥2 +18𝑥2 +9𝑥2 +4𝑥2 +56𝑥 + 126𝑥+6 =30𝑥4 + 168𝑥3 + 39𝑥2 + 182𝑥 + 6
  • 11.
    NOW TRY YOURSELF • FIND DERIVATIVES WITH RESPECT TO 𝑥 • Y=(2𝑥 + 3) 5𝑥3 − 2 • Y=𝑥4 + 𝑥5 + 5𝑥6 + 3𝑥2 + 3𝑥3 − 9 • Y=3𝑥4 + 13𝑥3 − 9𝑥 + 15 • Y=(𝑥 + 1)(9𝑥 + 5)(𝑥2 − 9) • Y= 3𝑥2 + 5𝑥 − 9 • Y=(𝑥2 + 𝑥 − 1)(𝑥2 + 𝑥 + 1) • Y=(2X-1)(6X+1) • Y=7𝑥2 + 123𝑥 − 100
  • 12.
    Y= 𝑢 𝑣 then 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u𝑑𝑣 𝑑𝑥 𝑣2 • FIND THE DERIVATIVE OF 𝑦 = 1+𝑥 1+𝑥2 • HERE 𝑦 = 1+𝑥 1+𝑥2 = 𝑢 𝑣 • LET 𝑢 = (1 + 𝑥) 𝑣 = (1 + 𝑥2) • 𝑑𝑢 𝑑𝑥 = 0 + 1 𝑑𝑣 𝑑𝑥 = 0 + 2𝑥 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 • = (1+𝑥2) (1)−(1+𝑥)(2x) (1+𝑥2)2 = 1 + 𝑥2 − 2𝑥 − 2𝑥2 (1 + 𝑥2)2 = 1−2𝑥−𝑥2 (1+𝑥2)2 • FIND DERIVATIVE 𝑦 = 𝑥2+𝑥+1 𝑥2−𝑥+1 • HERE 𝑦 = 𝑥2+𝑥+1 𝑥2−𝑥+1 = 𝑢 𝑣 • LET 𝑢 = (𝑥2 + 𝑥 + 1) 𝑣 = (𝑥2 − 𝑥 + 1) • 𝑑𝑢 𝑑𝑥 = 2𝑥 + 1 𝑑𝑣 𝑑𝑥 = 2𝑥 − 1 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 • = (𝑥2−𝑥+1) (2X+1)−(𝑥2+𝑥+1)(2x−1) (1−𝑥+𝑥2)2 = =
  • 13.
    Find derivati𝑣𝑒𝑠 w.r.t.𝑥 • Y= 3 2−5𝑥 • HERE 𝑦 = 3 2−5𝑥 = 𝑢 𝑣 • LET 𝑢 = 3 𝑣 = (2 − 5𝑥) • 𝑑𝑢 𝑑𝑥 = 0 𝑑𝑣 𝑑𝑥 = −5 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 • = (2−5𝑥)(0)−3(−5) (2−5𝑥)2 = 0 + 15 (2 − 5𝑥)2 = 15 (2−5𝑥)2 • Y=1+ 1 1+ 1 𝑥 • Y=1+ 1 1 1 + 1 𝑥 =1+ 1 𝑥+1 𝑥 =1+ 𝑥 𝑥+1 = 1 1 + 𝑥 𝑥+1 = 𝑥+1+𝑥 𝑥+1 = 2𝑥+1 𝑥+1 • NOW 𝑦 = 2𝑥+1 𝑥+1 • 𝑢 = 2𝑥 + 1 𝑣 = • 𝑑𝑢 𝑑𝑥 = 2 𝑑𝑣 𝑑𝑥 = 1 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 = 𝑥+1 2 −(2𝑥+1)(1) (𝑥+1)2 = 2𝑥+2−2𝑥−1 (𝑥+1)2 = 1 (𝑥+1)2
  • 14.
    Find derivative of 3 (𝑥+2)(𝑥+3) •𝑦 = 3 (𝑥+2)(𝑥+3) • 𝑦 = 3 𝑥2+3𝑥+2𝑥+6 • ∴ 𝑦= 3 𝑥2+5𝑥+6 • NOW 𝑦 = 3 𝑥2+5𝑥+6 • 𝑢 = 3 𝑣 = 𝑥2 + 5𝑥 + 6 • 𝑑𝑢 𝑑𝑥 = 0 𝑑𝑣 𝑑𝑥 = 2𝑥 + 5 • 𝒅𝒚 𝒅𝒙 = 𝒅 𝒖 𝒗 𝒅𝒙 = v 𝒅𝒖 𝒅𝒙 − u 𝒅𝒗 𝒅𝒙 𝒗𝟐 • = (𝑥2+5𝑥+6)(0)−𝟑(𝟐𝒙+𝟓) (𝑥2+5𝑥+6)𝟐 • = −𝟑(𝟐𝒙+𝟓) (𝑥2+5𝑥+6)𝟐 • OR • = −𝟔𝒙−𝟏𝟓 (𝑥2+5𝑥+6)𝟐
  • 15.
    (Find derivative of𝑥 + 2𝑥+3 𝑥+2 𝑥 + 4𝑥+10 𝑥+3 • 𝑦 = 𝑥 + 2𝑥+3 𝑥+2 𝑥 + 4𝑥+10 𝑥+3 • 𝑦 = 𝑥 1 + 2𝑥+3 𝑥+2 𝑥 1 + 4𝑥+10 𝑥+3 • 𝑦 = 𝑥 𝑥+2 + 2𝑥+3 𝑥+2 𝑥 𝑥+3 + 4𝑥+10 𝑥+3 • 𝑦 = 𝑥2+2𝑥+2𝑥+3 𝑥+2 𝑥23𝑥+4𝑥+10 𝑥+3 • 𝑦 = 𝑥2+4𝑥+3 𝑥+2 𝑥2+7𝑥+10 𝑥+3 • 𝑦 = 𝑥2+3𝑥+𝑥+3 𝑥+2 𝑥2+5𝑥+2𝑥+10 𝑥+3 • 𝑦 = 𝑥 𝑥+3 +1(𝑥+3) 𝑥+2 𝑥 𝑥+5 +2(𝑥+5) (𝑥+3) • 𝑦 = 𝑥+1 𝑥+3 𝑥+2 𝑥+5 𝑥+2 𝑥+3 = 𝑥 + 1 𝑥 + 5 • 𝑦 = 𝑥 + 1 𝑥 + 5 • 𝑦 = 𝑥 𝑥 + 5 + 1 𝑥 + 5 • 𝑦 = 𝑥2 + 5𝑥 + 𝑥 + 5 • 𝑦 = 𝑥2 + 6𝑥 + 5 • NOW • 𝑑𝑦 𝑑𝑥 = 𝑑 (𝑥2+6𝑥+5) 𝑑𝑥 • 𝑑𝑦 𝑑𝑥 = 2𝑥 + 6
  • 16.
    Find 𝑑𝑦 𝑑𝑥 if 𝑥 +1 𝑦 + 1 = 18 • 𝑥 + 1 𝑦 + 1 = 18 • 𝑦 + 1 = 18 𝑥+1 • 𝑦 = 18 𝑥+1 − 1 • 𝑦 = 18−1 𝑥+1 𝑥+1 • 𝑦 = 18−𝑥−1 𝑥+1 • 𝑦= 17−𝑥 𝑥+1 • Now 𝑦 = 17−𝑥 𝑥+1 • LET 𝑢 = 17 − 𝑥 𝑣 = 𝑥 + 1 • 𝑑𝑢 𝑑𝑥 = −1 𝑑𝑣 𝑑𝑥 = 1 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 • 𝑑𝑦 𝑑𝑥 = 𝑥+1 −1 −(17−𝑥)(1) 𝑥+1 2 • 𝑑𝑦 𝑑𝑥 = −𝑥−1−17+𝑥 𝑥+1 2 • = −18 𝑥+1 2
  • 17.
    F𝑖𝑛𝑑 𝑑𝑦 𝑑𝑥 𝑖𝑓 𝑥𝑦 +𝑥 + 𝑦 − 2 = 0 • 𝑥𝑦 + 𝑥 + 𝑦 − 2 = 0 • 𝑥𝑦 + 𝑦 = 2 − 𝑥 • 𝑦 𝑥 + 1 = 2 − 𝑥 • 𝑦 = 2−𝑥 𝑥+1 • N𝑜𝑤 𝑦 = 2−𝑥 𝑥+1 • LET 𝑢 = 2 − 𝑥 𝑣 = 𝑥 + 1 • 𝑑𝑢 𝑑𝑥 = −1 𝑑𝑣 𝑑𝑥 = 1 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 • 𝑑𝑦 𝑑𝑥 = 𝑥+1 −1 −(2−𝑥)(1) 𝑥+1 2 • = −𝑥−1−2+𝑥 𝑥+1 2 • = −3 𝑥+1 2
  • 18.
    𝐴𝑝𝑝𝑙𝑖𝑐𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒𝑠 • If y = 𝑥𝑛 then 𝑑𝑦 𝑑𝑥 =n𝑥𝑛−1 • If y = x then 𝑑𝑦 𝑑𝑥 = 1 • If y=c then 𝑑𝑦 𝑑𝑥 =0 • If y=𝑒𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑒𝑥 • If y= 𝑎𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑎𝑥 loge a • 𝐼𝑓𝑦 =loge x then 𝑑𝑦 𝑑𝑥 = 1 𝑥 • 𝐹𝑖𝑛𝑑 𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑥3 𝑒𝑥 𝑤𝑖𝑡ℎ 𝑟𝑒𝑠𝑝𝑒𝑐𝑡 𝑡𝑜 𝑥 𝐻𝑒𝑟𝑒 𝑦 = 𝑥3 𝑒𝑥 𝑢 = 𝑥2 𝑣 = 𝑒𝑥  𝑑𝑢 𝑑𝑥 = 2𝑥 𝑑𝑣 𝑑𝑥 = 𝑒𝑥  𝑑𝑦 𝑑𝑥 = 𝑣 𝑑𝑢 𝑑𝑥 + 𝑢 𝑑𝑣 𝑑𝑥 = (𝑒𝑥)(2𝑥)+(𝑥2)(𝑒𝑥) = 𝑥𝑒𝑥(2 + 𝑥)
  • 19.
    𝐴𝑝𝑝𝑙𝑖𝑐𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒𝑠 • If y = 𝑥𝑛 then 𝑑𝑦 𝑑𝑥 =n𝑥𝑛−1 • If y = x then 𝑑𝑦 𝑑𝑥 = 1 • If y=c then 𝑑𝑦 𝑑𝑥 =0 • If y=𝑒𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑒𝑥 • If y= 𝑎𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑎𝑥 loge a • 𝐼𝑓𝑦 =loge x then 𝑑𝑦 𝑑𝑥 = 1 𝑥 • 𝑓𝑖𝑛𝑑 𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑥4 log 𝑥 • 𝐻𝑒𝑟𝑒 𝑦 = 𝑥4 log 𝑥 • 𝑢 = 𝑥4 𝑣 = 𝑙𝑜𝑔𝑥 • 𝑑𝑢 𝑑𝑥 = 4𝑥3 𝑑𝑣 𝑑𝑥 = 1 𝑥 • 𝑑𝑦 𝑑𝑥 = 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 = 𝑙𝑜𝑔𝑥 4𝑥3 − 𝑥4 1 𝑥 𝑙𝑜𝑔𝑥 2 = 𝑙𝑜𝑔𝑥 4𝑥3 − 𝑥3 𝑙𝑜𝑔𝑥 2 = 𝑥3 4𝑙𝑜𝑔𝑥−1 𝑙𝑜𝑔𝑥 2
  • 20.
    𝐴𝑝𝑝𝑙𝑖𝑐𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒𝑠 • If y = 𝑥𝑛 then 𝑑𝑦 𝑑𝑥 =n𝑥𝑛−1 • If y = x then 𝑑𝑦 𝑑𝑥 = 1 • If y=c then 𝑑𝑦 𝑑𝑥 =0 • If y=𝑒𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑒𝑥 • If y= 𝑎𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑎𝑥 loge a • 𝐼𝑓𝑦 =loge x then 𝑑𝑦 𝑑𝑥 = 1 𝑥 • 𝐹𝑖𝑛𝑑 𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑥3/2 4𝑥 • 𝑢 = 𝑥3/2 𝑣 = 4𝑥 • 𝑑𝑢 𝑑𝑥 = 3 2 𝑥 3 2 −1 = 3 2 𝑥 1 2 𝑑𝑣 𝑑𝑥 = 4𝑥 log 4 • 𝑑 𝑢 𝑣 𝑑𝑥 = v 𝑑𝑢 𝑑𝑥 − u 𝑑𝑣 𝑑𝑥 𝑣2 = 𝑙𝑜𝑔𝑥 4𝑥3 − 𝑥4 1 𝑥 𝑙𝑜𝑔𝑥 2 = 𝑙𝑜𝑔𝑥 4𝑥3 − 𝑥3 𝑙𝑜𝑔𝑥 2 = 𝑥3 4𝑙𝑜𝑔𝑥−1 𝑙𝑜𝑔𝑥 2
  • 21.
    𝐴𝑝𝑝𝑙𝑖𝑐𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒𝑠 • If y = 𝑥𝑛 then 𝑑𝑦 𝑑𝑥 =n𝑥𝑛−1 • If y = x then 𝑑𝑦 𝑑𝑥 = 1 • If y=c then 𝑑𝑦 𝑑𝑥 =0 • If y=𝑒𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑒𝑥 • If y= 𝑎𝑥 then 𝑑𝑦 𝑑𝑥 = 𝑎𝑥 loge a • 𝐼𝑓𝑦 =loge x then 𝑑𝑦 𝑑𝑥 = 1 𝑥