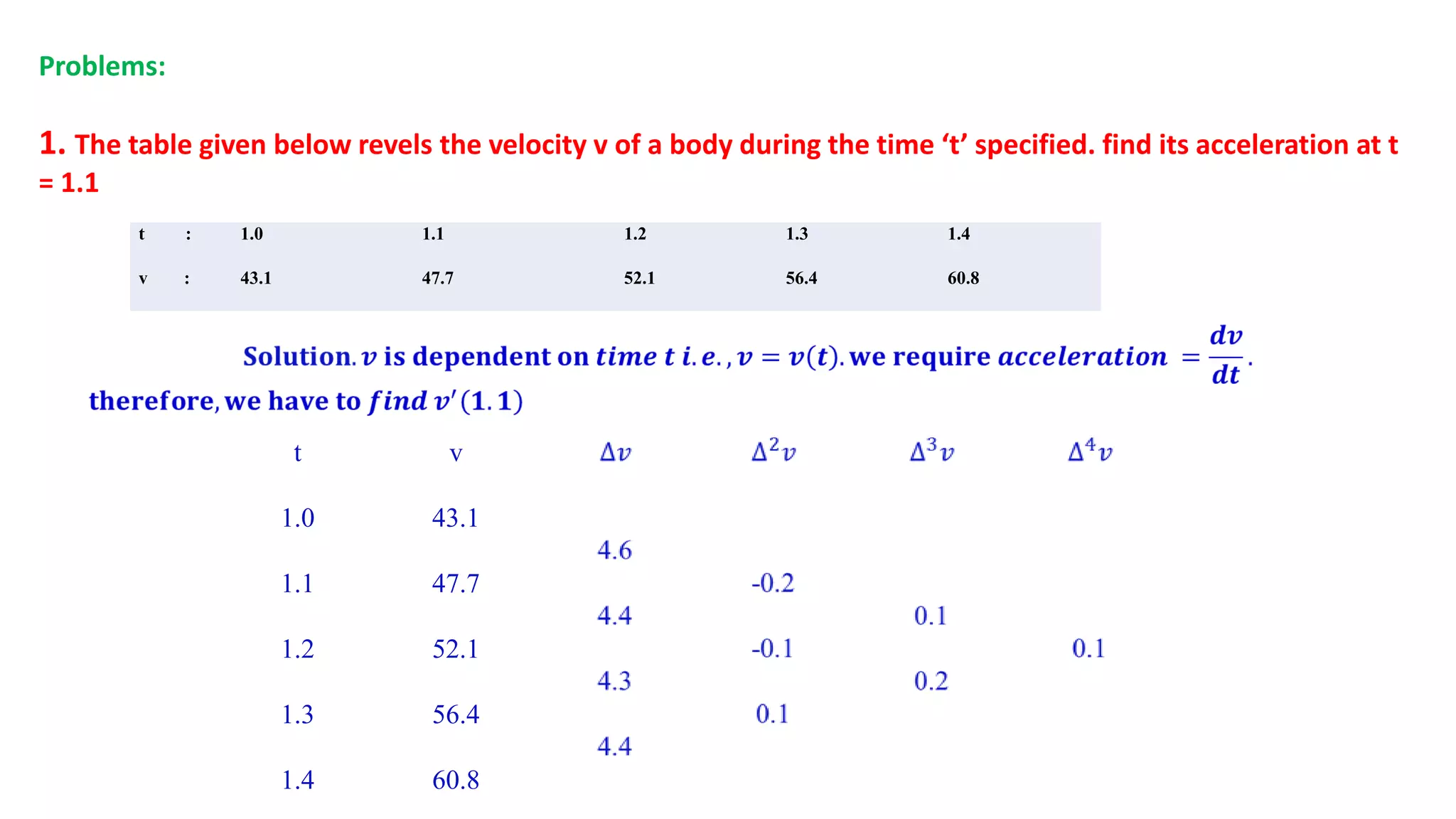
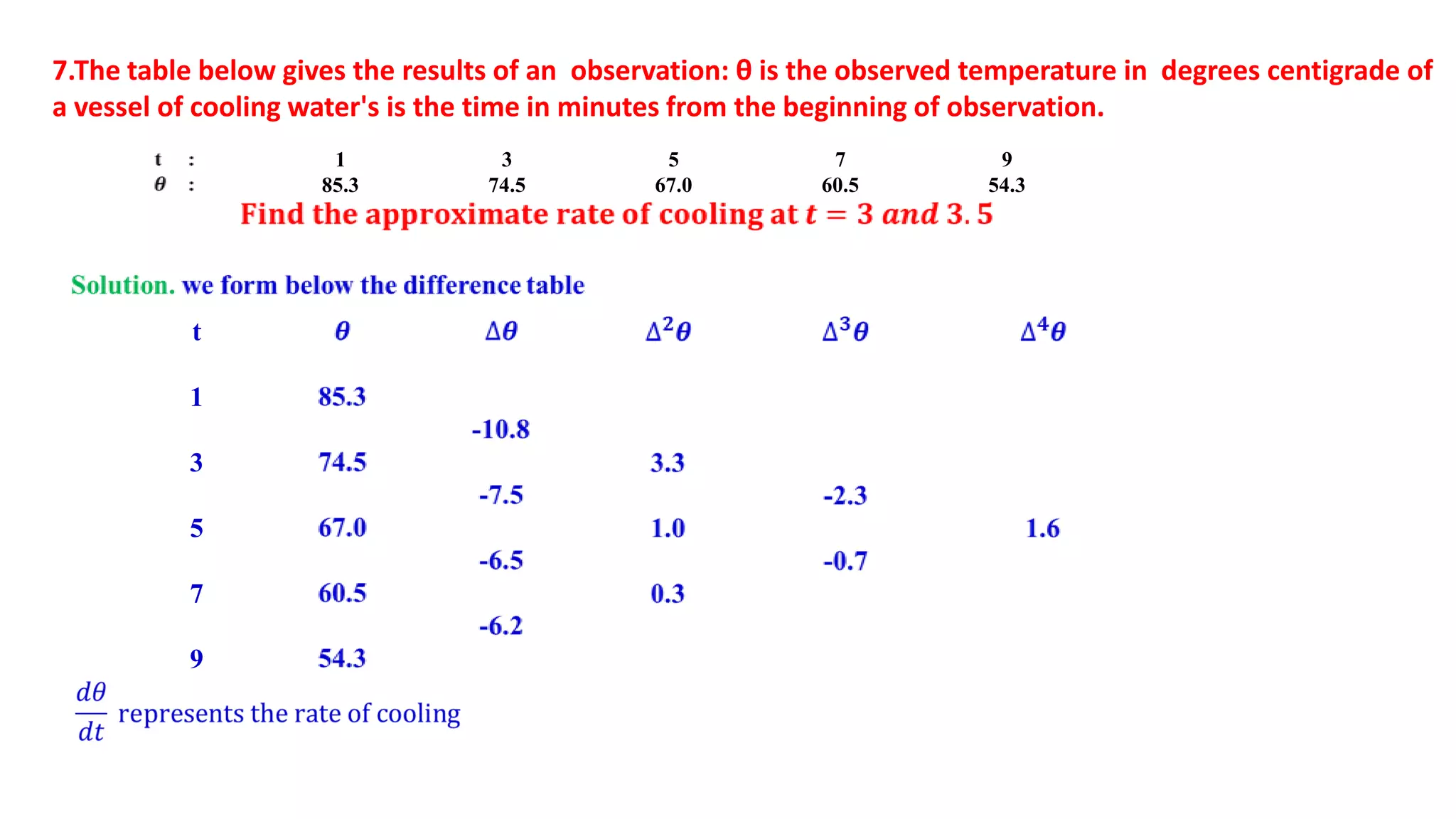
This document provides an overview of numerical differentiation and integration methods. It discusses Newton's forward and backward difference formulas for computing derivatives, as well as Newton-Cote's formula, the trapezoidal rule, and Simpson's one-third and three-eighths rules for numerical integration. Examples of applying these methods to real-world problems are provided. The document also compares Simpson's one-third and three-eighths rules, noting their different assumptions about the polynomial order of the integrated function and requirements for the number of intervals.

1. NUMERICAL METHODS
(06CT42)
Dr. N. Meenakshi Sundaram
Asst. Prof. of Physics
Vivekananda College
Tiruvedakam West - Madurai

2. CONTENTS
Newton’s forward difference formula to get the derivative
Newton’s backward difference formula to compute the derivative
Newton-Cote’s formula
Trapezoidal rule
Simpson’s one-third rule
Simpson’s three-eighths rule
NUMERICAL OF DIFFERENTATION AND INTEGRATION

3. UNIT – IV Numerical Differentiation and Integration
Numerical Differentiation
Introduction
We found the polynomial curve y = f (x), passing through the (n+1) ordered pairs (xi, yi), i=0, 1, 2…n.
Now we are trying to find the derivative value of such curves at a given x = xk (say), whose x0 < xk < xn.
To get derivative, we first find the curve y = f (x) through the points and then differentiate and get its value
at the required point.
If the values of x are equally spaced. We get the interpolating polynomial due to Newton-Gregory.
• If the derivative is required at a point nearer to the starting value in the table, we use Newton’s
forward interpolation formula.
• If we require the derivative at the end of the table, we use Newton’s backward interpolation
formula.
• If the value of derivative is required near the middle of the table value, we use one of the central
difference interpolation formulae

11. Problems:
1. The table given below revels the velocity v of a body during the time ‘t’ specified. find its acceleration at t
= 1.1
t : 1.0 1.1 1.2 1.3 1.4
v : 43.1 47.7 52.1 56.4 60.8
t
1.0
1.1
1.2
1.3
1.4
v
43.1
47.7
52.1
56.4
60.8

13. 2. A rod is rotating in a plane. The following table gives the angle θ (in radians) through which the rod has
turned for various values of time t (seconds).Calculate the angular velocity and angular acceleration of the
rod at=0.6 seconds.
t : 0 0.2 0.4 0.6 0.8 1.0
0 0.12 0.49 1.12 2.02 3.20
Solution. We form the difference table below:
t
0
0.2
0.4
0.6
0.8
1.0

16. x -3 -2 -1 0 1 2 3
y 81 16 1 0 1 16 81

18. x 0 1 2 3 4 5 6
1 0.5 1/3 1/4 1/5 1/6 1/7

19. 5. A river is 80 meters wide. The depth '"d'" in meters at a distance x meters from one bank is
given by the following table. Calculate the area of cross section of the river using
Simpson' s rule.

20. x
:
0 10 20 30 40 50 60 70 80
d
:
0 4 7 9 12 15 14 8 3

23. 7.The table below gives the results of an observation: θ is the observed temperature in degrees centigrade of
a vessel of cooling water's is the time in minutes from the beginning of observation.
1
85.3
3
74.5
5
67.0
7
60.5
9
54.3
t
1
3
5
7
9

25. x
:
50 51 52 53 54 55 56
3.6840 3.7084 3.7325 3.7563 3.7798 3.8030 3.8259
x
50
51
52
53
54
55
56
y
3.6840
3.7084
3.7325
3.7563
3.7798
3.8030
3.8259

28. x 0 0.2 0.4 0.6 0.8 1.0
1 0.96154 0.86207 0.73529 0.60976 0.50000

29. x : 4 4.2 4.4 4.6 4.8 5.0 5.2
1.386294
4
1.4350845 1.4816045 1.5260563 1.5686159 1.6094379 1.6486586

31. 2. What is the nature of y (x) in the case of trapezoidal rule?
In trapezoidal rule, y (x) is a linear function of x.
3. State the nature of y (x) and number of intervals in the case of Simpson’s one-third rule?
In Simpson’s one-third rule, y (x) is a polynomial of degree two. To apply this rule n, the number of
intervals must be even.

32. 4. What is the nature of y (x) in the case of Simpson’s three-eighths rule and when it is applicable?
In Simpson’s third-eighths rule, y (x) is a polynomial of degree three. This rule is applicable if n, the number
of intervals is a multiple of 3.
5. Differentiate between Simpson’s one-third rule and Simpson’s three-eighths rule.
S.No Simpson’s one-third rule Simpson’s three-eighths rule
1 y (x) is a polynomial of degree two y (x) is a polynomial of degree three
2 The number of intervals must be even. The number of intervals is a multiple of 3.

33. Reference Text Book: Numerical Methods – P.Kandasamy, K.Thilagavathy & K.Gunavathi,
S.Chand & Company Ltd., New Delhi, 2014.

34. Thank you