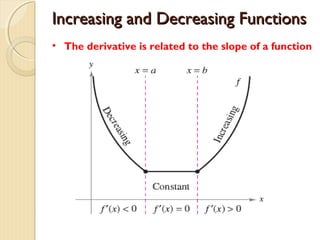
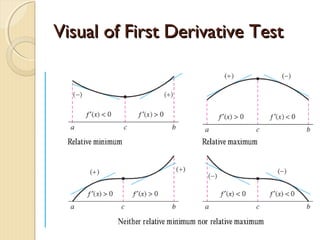
The document discusses increasing and decreasing functions and the first derivative test. It defines that a function is increasing if the derivative is positive, decreasing if the derivative is negative, and constant if the derivative is zero. It provides examples of finding the intervals where a function is increasing or decreasing by identifying critical numbers and testing points in each interval. The document also summarizes the first derivative test, stating that a critical point is an extremum if the derivative changes sign there, and whether it is a maximum or minimum depends on if the derivative changes from negative to positive or positive to negative.

1. Increasing and Decreasing Functions and
the First Derivative Test
AP Calculus – Section 3.3
Objectives:
1.Find
the intervals on which a function is
increasing or decreasing.
2.Use
the First Derivative Test to classify
extrema as either a maximum or a minimum.

2. Increasing and Decreasing Functions
• The derivative is related to the slope of a function

3. Increasing and Decreasing Functions
On an interval in which a function f is
continuous and differentiable, a
function is…
increasing if f ‘(x) is positive on that
interval, ( f ‘ (x) > 0 )
decreasing if f ‘(x) is negative on that
interval, and ( f ‘ (x) < 0 )
constant if f ‘(x) = 0 on that interval.

4. Visual Example
f ‘(x) < 0 on (-5,-2)
f(x) is decreasing on (-5,-2)
f ‘(x) = 0 on (-2,1)
f(x) is constant on (-2,1)
f ‘(x) > 0 on (1,3)
f(x) is increasing on (1,3)

5. Finding Increasing/Decreasing
Intervals for a Function
To find the intervals on which a function is
increasing/decreasing:
1.Find critical numbers. - These determine
the boundaries of your intervals.
2.Pick a random x-value in each interval.
3.Determine the sign of the derivative on
that interval.

6. Example
Find the intervals on which the function
3
f ( x) = x − x is increasing and decreasing.
2
3
2
Critical numbers:
f ' ( x) = 3x 2 − 3 x
3x 2 − 3x = 0
3 x( x − 1) = 0
x = {0,1}

7. Example
Test an x-value in each interval.
Interval
Test Value
f ‘(x)
(−∞,0)
(0,1)
(1, ∞)
−1
1
2
2
f ' (−1) = 6
3
1
f '  = −
4
2
f ' ( 2) = 6
f(x) is increasing on (−∞,0) and (1, ∞)
.
f(x) is decreasing on (0,1).

8. Practice
Find the intervals on which the function
f ( x) = x 3 + 3 x 2 − 9 x is increasing and decreasing.
Critical numbers:
f ' ( x) = 3x 2 + 6 x − 9
3x 2 + 6 x − 9 = 0
3( x 2 + 2 x − 3) = 0
3( x + 3)( x − 1) = 0
x = {−3,1}

9. f ' ( x) = 3x 2 + 6 x − 9
Practice
Test an x-value in each interval.
Interval
(−∞,−3)
(−3,1)
(1, ∞)
Test Value
−4
0
2
f ‘(x)
f ' (−4) = 15 f ' ( 0) = −9
f ' (2) = 15
f(x) is increasing on (−∞ ,− 3) and (1, ∞)
.
f(x) is decreasing on (−3,1)
.

10. The First Derivative Test
AP Calculus – Section 3.3

11. The First Derivative Test
Summary
The
point where the first derivative
changes sign is an extrema.

12. The First Derivative Test
If c is a critical number of a function f, then:
If f ‘(c) changes from negative to positive
at c, then f(c) is a relative minimum.
If f ‘(c) changes from positive to negative
at c, then f(c) is a relative maximum.
If f ‘(c) does not change sign at c, then f(c)
is neither a relative minimum or
maximum.
GREAT picture on page 181!

13. Visual of First Derivative Test

14. Find all intervals of increase/decrease and
all relative extrema.
f ( x) = x 2 + 8 x + 10
Critical Points:
Test:
(−∞,−4)
f ' ( x) = 2 x + 8
2x + 8 = 0
x = −4
f ' (−5) = 2(−5) + 8 = −2
f is decreasing
CONCLUSION:
Test:
(−4, ∞)
f ' ( 0) = 8
f is increasing
f is decreasing before -4 and
increasing after -4; so f(-4) is a MINIMUM.