1. The document derives formulas for the nth derivative of several standard functions: - y = xm yields Dn xm = m!/(m-n)! xm-n - y = ax + bm yields Dn(ax + bm) = m!/(m-n)! an ax + bm-n - y = 1/(ax + b) yields Dn 1/(ax + b) = (-1)n n! an/(ax + b)n+1 2. It also provides the nth derivatives of more complex functions like logarithmic and fractional functions by using the above formulas. 3. Several problems are worked out as examples to find the nth derivative of various fractional functions.

1. nth DERIVATIVES OF SOME
STANDARD RESULTS
Dr. Soya Mathew

2. I. Derivation for the nth derivative of 𝑦 = 𝑥𝑚
; where m is a positive integer
Proof:-
Let 𝑦 = 𝑥𝑚
𝑦1 = 𝑚 𝑥𝑚−1
.
𝑦2 = 𝑚(𝑚 − 1) 𝑥𝑚−2
.
𝑦3 = 𝑚(𝑚 − 1)(𝑚 − 2) 𝑥𝑚−3
.
……………………………………………………..
𝑦𝑛 = 𝑚 𝑚 − 1 𝑚 − 2 … (𝑚 − (𝑛 − 1)) 𝑥𝑚−𝑛
.

3. 𝑦𝑛 = 𝑚 𝑚 − 1 𝑚 − 2 … (𝑚 − 𝑛 + 1) 𝑥𝑚−𝑛.
⇒ 𝑦𝑛 =
𝑚 𝑚−1 𝑚−2 … 𝑚−𝑛+1 𝑚−𝑛 …2.1
𝑚−𝑛 𝑚−𝑛−1 …2.1
𝑥𝑚−𝑛.
⇒ 𝑦𝑛 =
𝑚!
𝑚−𝑛 !
𝑥𝑚−𝑛.
∴ 𝑫𝒏 𝒙𝒎 =
𝒎!
𝒎−𝒏 !
𝒙𝒎−𝒏.

4. Thus if 𝑦 = 𝑥𝑚, m is a positive integer and 𝑛 ≤ 𝑚, then
𝑦𝑛 =
𝑚!
𝑚−𝑛 !
𝑥𝑚−𝑛.
Note:
1. If 𝑦 = 𝑥𝑚, m is a positive integer and 𝑛 = 𝑚, then
𝑦𝑛 = 𝑛!
2. If 𝑦 = 𝑥𝑚
, m is a positive integer and 𝑛 > 𝑚, then
𝑦𝑛 = 0

5. II. Derivation for the nth derivative of 𝑦 = 𝑎𝑥 + 𝑏 𝑚
; where m is a positive
integer.
Proof:-
Let 𝑦 = 𝑎𝑥 + 𝑏 𝑚
𝑦1 = 𝑚 𝑎 𝑎𝑥 + 𝑏 𝑚−1.
𝑦2 = 𝑚(𝑚 − 1) 𝑎2 𝑎𝑥 + 𝑏 𝑚−2.
𝑦3 = 𝑚(𝑚 − 1)(𝑚 − 2) 𝑎3 𝑎𝑥 + 𝑏 𝑚−3.
………………………………………………………………………..
𝑦𝑛 = 𝑚 𝑚 − 1 𝑚 − 2 … (𝑚 − 𝑛 − 1 ) 𝑎𝑛 𝑎𝑥 + 𝑏 𝑚−𝑛.

6. ⇒ 𝑦𝑛 = 𝑚 𝑚 − 1 𝑚 − 2 … (𝑚 − 𝑛 + 1) 𝑎𝑛 𝑎𝑥 + 𝑏 𝑚−𝑛.
⇒ 𝑦𝑛 =
𝑚 𝑚−1 𝑚−2 … 𝑚−𝑛+1 𝑚−𝑛 …2.1
𝑚−𝑛 𝑚−𝑛−1 …2.1
𝑎𝑛 𝑎𝑥 + 𝑏 𝑚−𝑛.
⇒ 𝑦𝑛 =
𝑚!
𝑚−𝑛 !
𝑎𝑛 𝑎𝑥 + 𝑏 𝑚−𝑛.
∴ 𝑫𝒏(𝒂𝒙 + 𝒃)𝒎 =
𝒎!
𝒎−𝒏 !
𝒂𝒏 𝒂𝒙 + 𝒃 𝒎−𝒏.

7. Thus if 𝑦 = 𝑎𝑥 + 𝑏 𝑚, m is a positive integer and 𝑛 ≤ 𝑚, then
𝑦𝑛 =
𝑚!
𝑚−𝑛 !
𝑎𝑛 𝑎𝑥 + 𝑏 𝑚−𝑛.
Note:
1. If 𝑦 = 𝑎𝑥 + 𝑏 𝑚, m is a positive integer and 𝑛 = 𝑚, then
𝑦𝑛 = 𝑛! 𝑎𝑛
2. If 𝑦 = 𝑎𝑥 + 𝑏 𝑚
, m is a positive integer and 𝑛 > 𝑚, then
𝑦𝑛 = 0

8. III. Derivation for the nth derivative of 𝑦 =
1
𝑎𝑥+𝑏
.
Proof:-
Let 𝑦 =
1
𝑎𝑥+𝑏
⇒ 𝑦 = 𝑎𝑥 + 𝑏 −1
𝑦1 = (−1) . 𝑎 𝑎𝑥 + 𝑏 −2.
𝑦2 = −1 −2 . 𝑎2 𝑎𝑥 + 𝑏 −3 = (−1)2 2! 𝑎2 𝑎𝑥 + 𝑏 −3.
𝑦3 = (−1)(−2)(−3) . 𝑎3 𝑎𝑥 + 𝑏 −4 = (−1)3 3! 𝑎3 𝑎𝑥 + 𝑏 −4
………………………………………………………………………………………………………

9. ⇒ 𝑦𝑛 = (−1)𝑛
𝑛! 𝑎𝑛
𝑎𝑥 + 𝑏 −(𝑛+1)
.
∴ 𝑫𝒏 𝟏
𝒂𝒙+𝒃
=
(−𝟏)𝒏 𝒏! 𝒂𝒏
𝒂𝒙+𝒃 𝒏+𝟏 .
Note:
𝐷𝑛 1
𝑎𝑥+𝑏 𝑚 = −1 𝑛 (𝑚+𝑛−1)!
𝑚−1 !
1
𝑎𝑥+𝑏 𝑚+𝑛 𝑎𝑛

10. IV. Derivation for the nth derivative of 𝑦 = 𝑙𝑜𝑔(𝑎𝑥 + 𝑏).
Proof:-
Let 𝑦 = 𝑙𝑜𝑔(𝑎𝑥 + 𝑏)
𝑦1 = 𝑎.
1
𝑎𝑥+𝑏
= 𝑎. 𝑎𝑥 + 𝑏 −1
𝑦2 = (−1) . 𝑎2 𝑎𝑥 + 𝑏 −2.
𝑦3 = −1 −2 . 𝑎3 𝑎𝑥 + 𝑏 −3 = (−1)2 2! 𝑎3 𝑎𝑥 + 𝑏 −3.
𝑦4 = (−1)(−2)(−3) . 𝑎4 𝑎𝑥 + 𝑏 −4 = (−1)3 3! 𝑎4 𝑎𝑥 + 𝑏 −4.
………………………………………………………………………………………………………

11. ⇒ 𝑦𝑛 = (−1)𝑛−1 (𝑛 − 1)! 𝑎𝑛 𝑎𝑥 + 𝑏 −𝑛.
∴ 𝑫𝒏 𝒍𝒐𝒈(𝒂𝒙 + 𝒃) =
(−𝟏)𝒏−𝟏 (𝒏−𝟏)! 𝒂𝒏
𝒂𝒙+𝒃 𝒏

12. Recall
1. 𝐷𝑛
𝑥𝑚
=
𝑚!
𝑚−𝑛 !
𝑥𝑚−𝑛
2. 𝐷𝑛
(𝑎𝑥 + 𝑏)𝑚
=
𝑚!
𝑚−𝑛 !
𝑎𝑛
𝑎𝑥 + 𝑏 𝑚−𝑛
.
3. 𝐷𝑛 1
𝑎𝑥+𝑏
=
(−1)𝑛 𝑛! 𝑎𝑛
𝑎𝑥+𝑏 𝑛+1
4. 𝐷𝑛 1
𝑎𝑥+𝑏 𝑚 =
−1 𝑛 𝑚+𝑛−1 ! 𝑎𝑛
𝑚−1 ! 𝑎𝑥+𝑏 𝑚+𝑛
5. 𝐷𝑛
𝑙𝑜𝑔(𝑎𝑥 + 𝑏) =
(−1)𝑛−1 (𝑛−1)! 𝑎𝑛
𝑎𝑥+𝑏 𝑛

13. Problems:
1. Find the nth derivative of
2𝑥−1
(𝑥 − 2)(𝑥 + 1)
Solution:
Let 𝑦 =
2𝑥−1
(𝑥 − 2)(𝑥 + 1)
Resolving into partial fraction, we get
𝑦 =
2𝑥−1
(𝑥 − 2)(𝑥 + 1)
=
𝐴
(𝑥 − 2)
+
𝐵
(𝑥 + 1)
… … … … … … (1)
⇒ 2𝑥 − 1 = 𝐴 𝑥 + 1 + 𝐵 𝑥 − 2
When 𝑥 = −1, 𝐵 = 1
When 𝑥 = 2, 𝐴 = 1

14. ∴ (1) ⇒ 𝑦 =
1
𝑥 − 2
+
1
𝑥 + 1
∴ 𝑦𝑛 = 𝐷𝑛 1
𝑥 −2
+ 𝐷𝑛 1
𝑥 + 1
⇒ 𝑦𝑛 =
−1 𝑛 𝑛!
𝑥 −2 𝑛+1 +
−1 𝑛 𝑛!
𝑥 + 1 𝑛+1
⇒ 𝑦𝑛 = −1 𝑛
𝑛!
1
𝑥 −2 𝑛+1 +
1
𝑥 + 1 𝑛+1

15. 2. Find the nth derivative of
1
(𝑥 + 2)(𝑥 − 1)
Solution:
Let 𝑦 =
1
(𝑥 + 2)(𝑥 − 1)
Resolving into partial fraction, we get
𝑦 =
1
(𝑥 + 2)(𝑥 − 1)
=
1
(𝑥 + 2)(−2 − 1)
+
1
(1 + 2)(𝑥 − 1)
⇒ 𝑦 = −
1
3
1
(𝑥 + 2)
+
1
3
1
(𝑥 − 1)

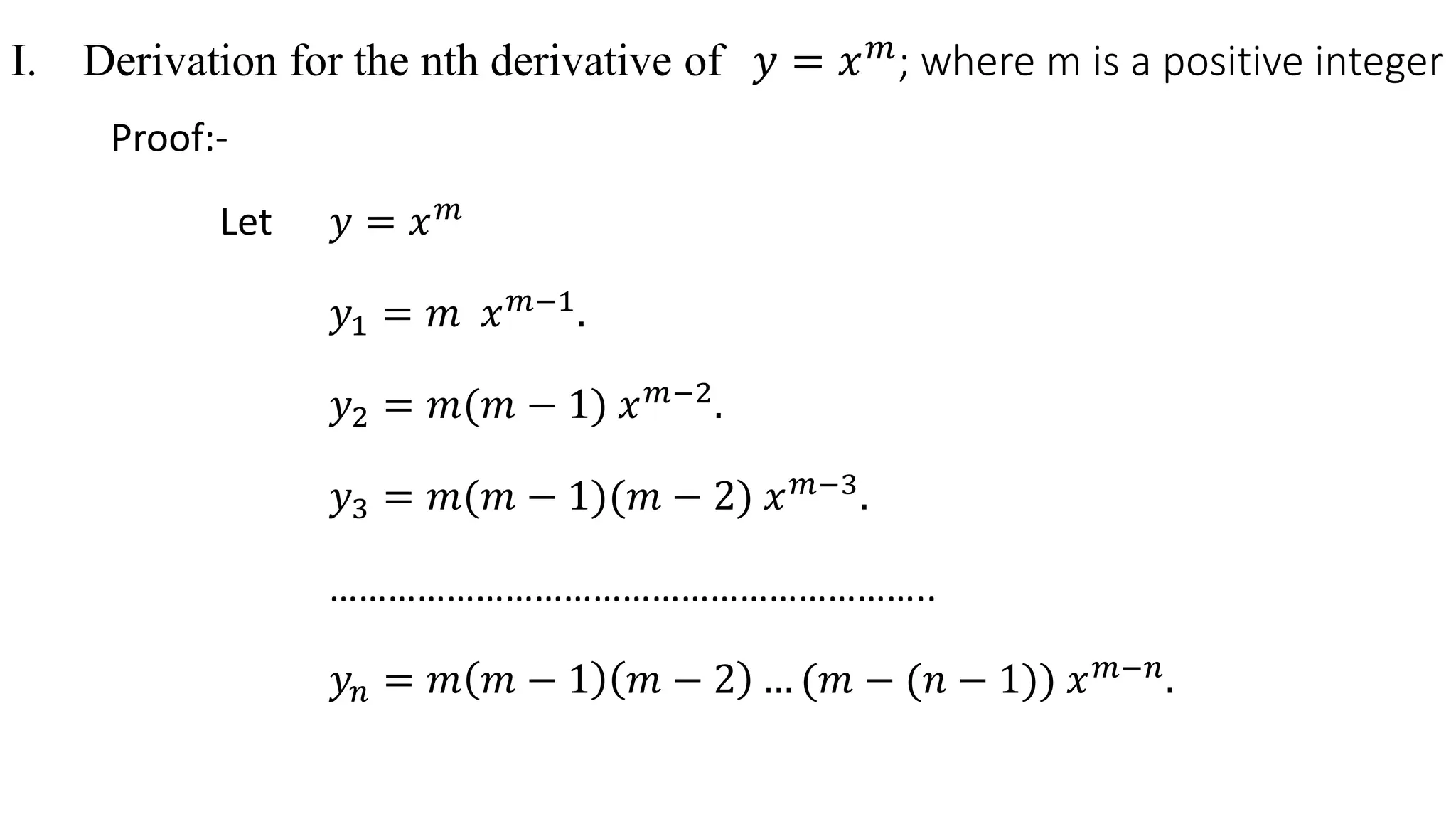
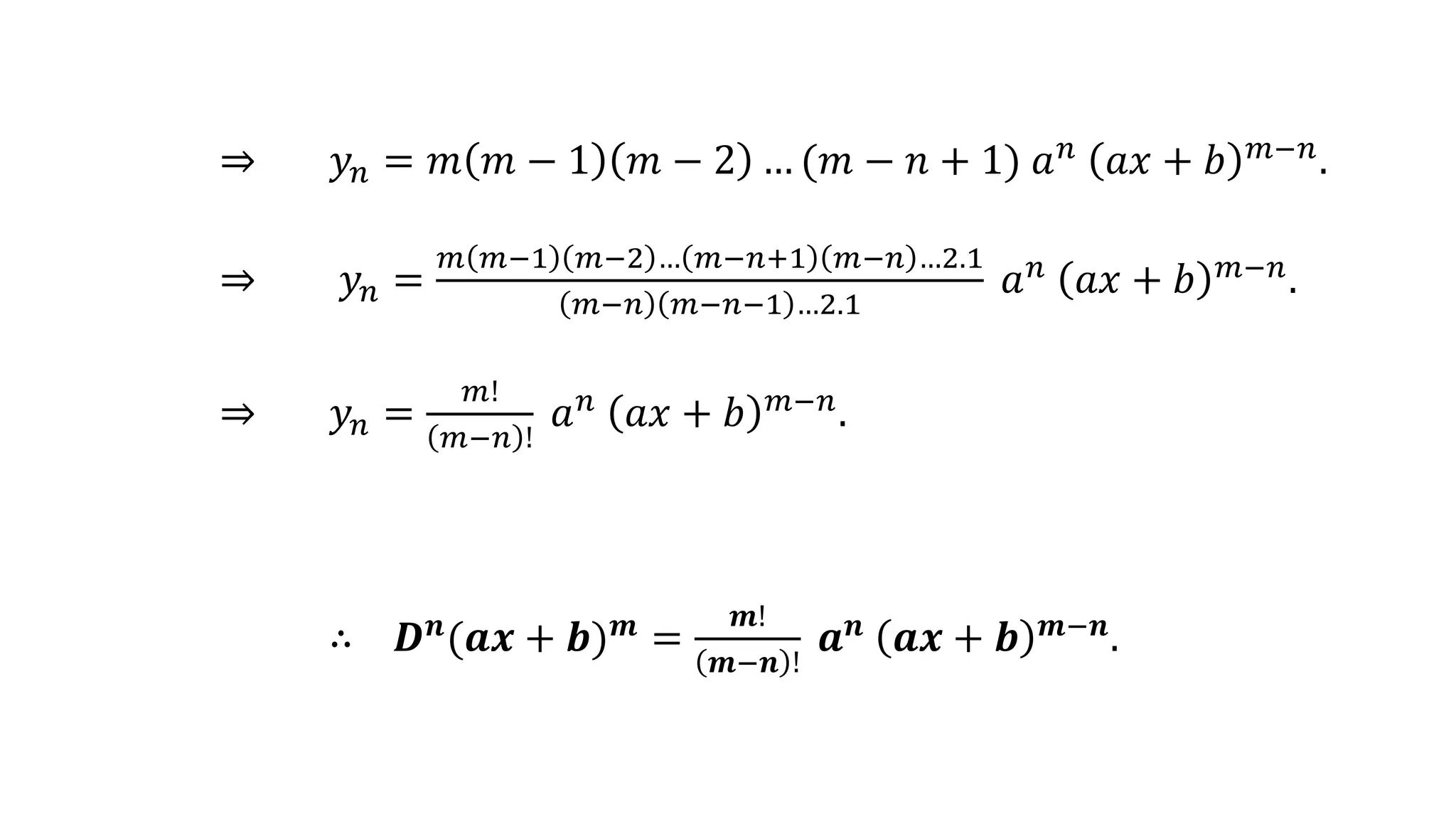
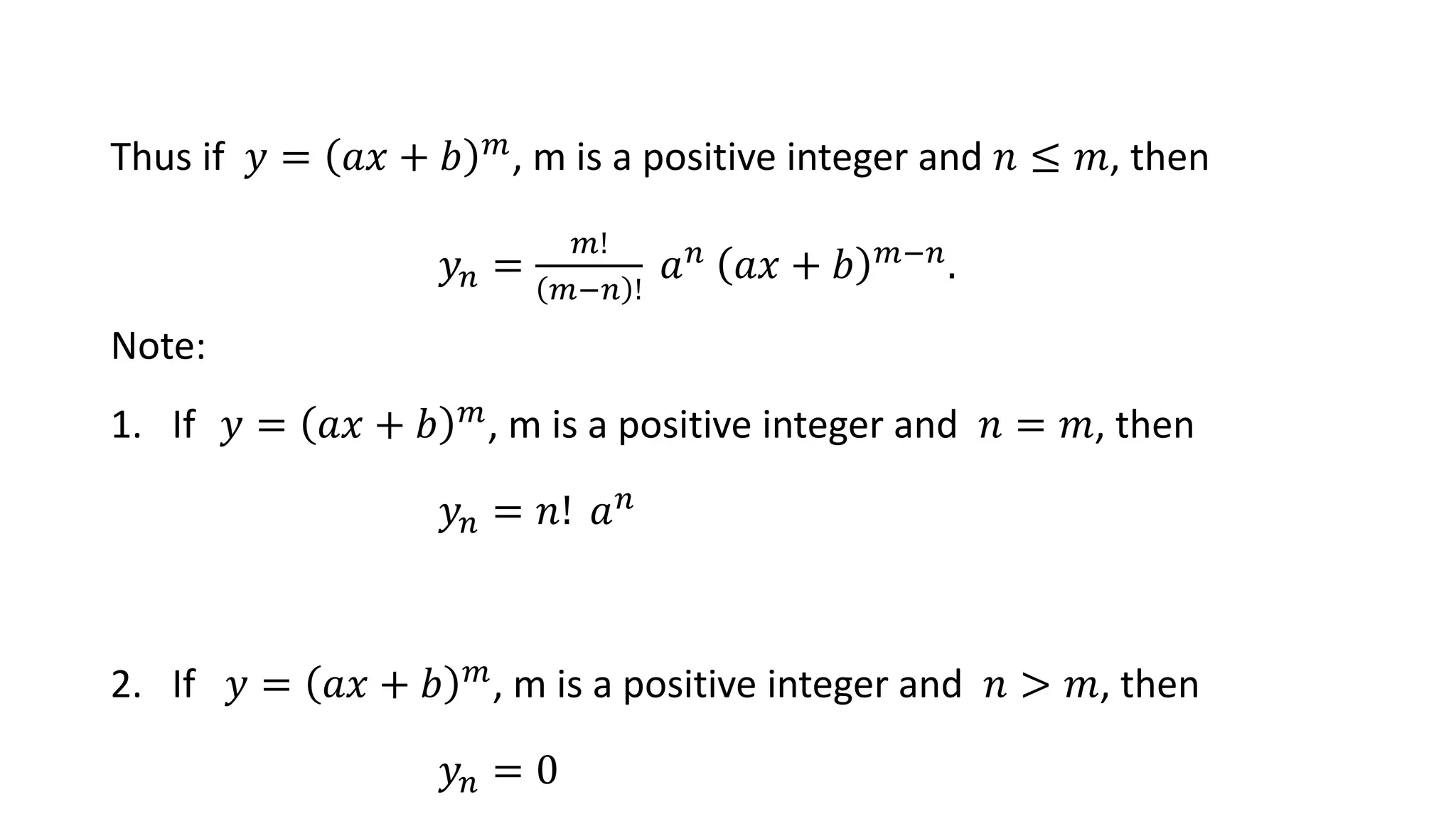
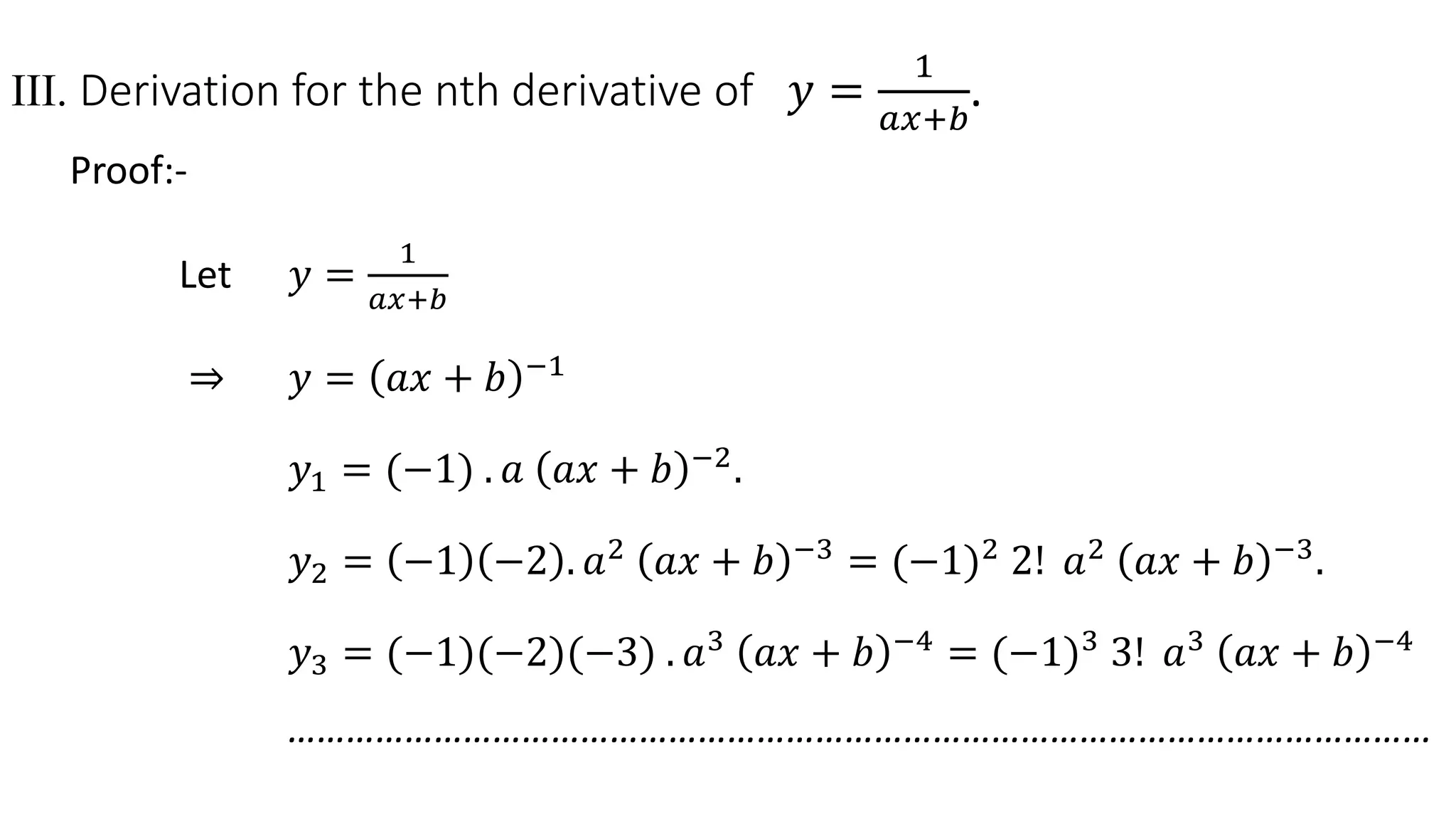
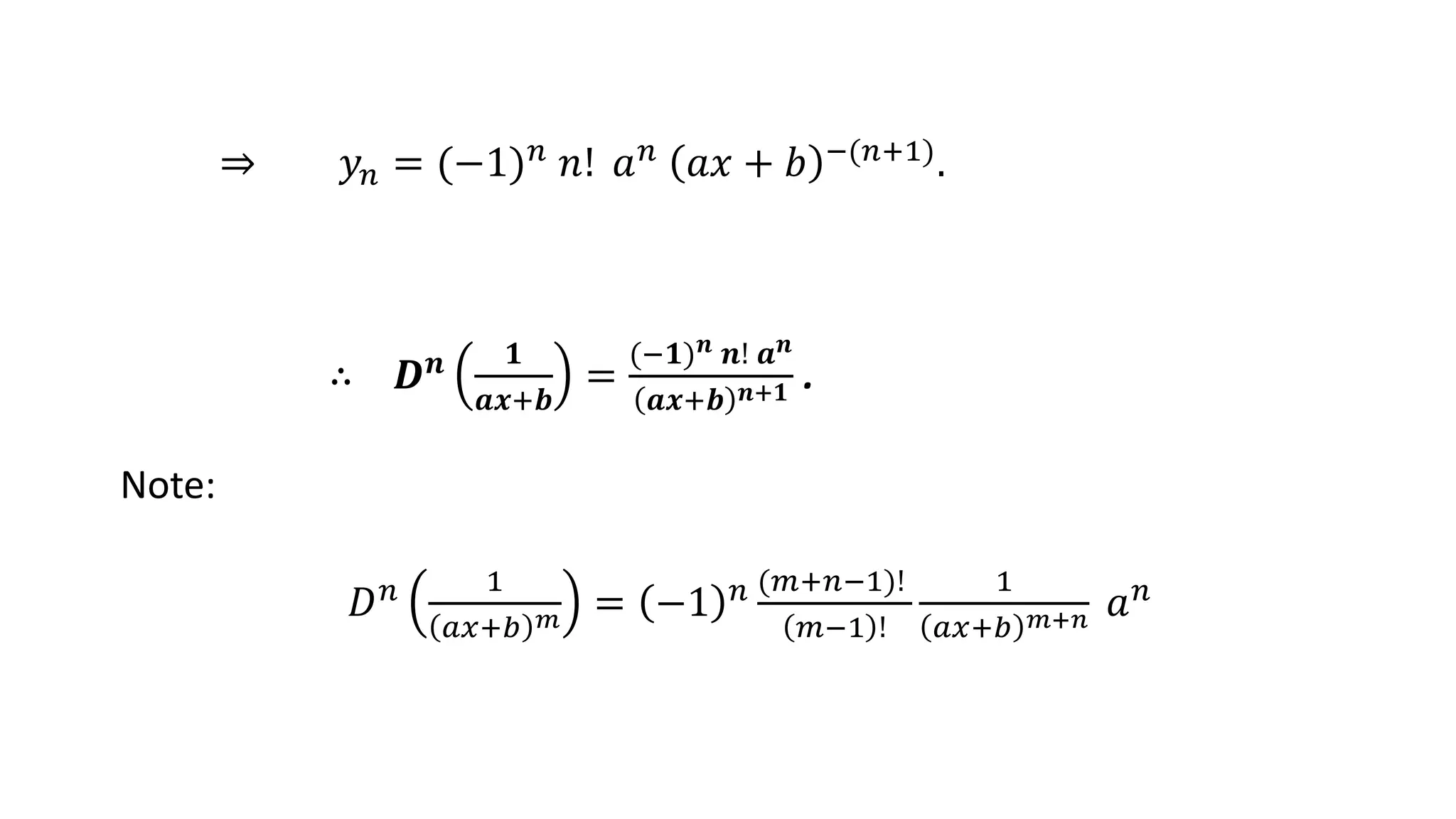
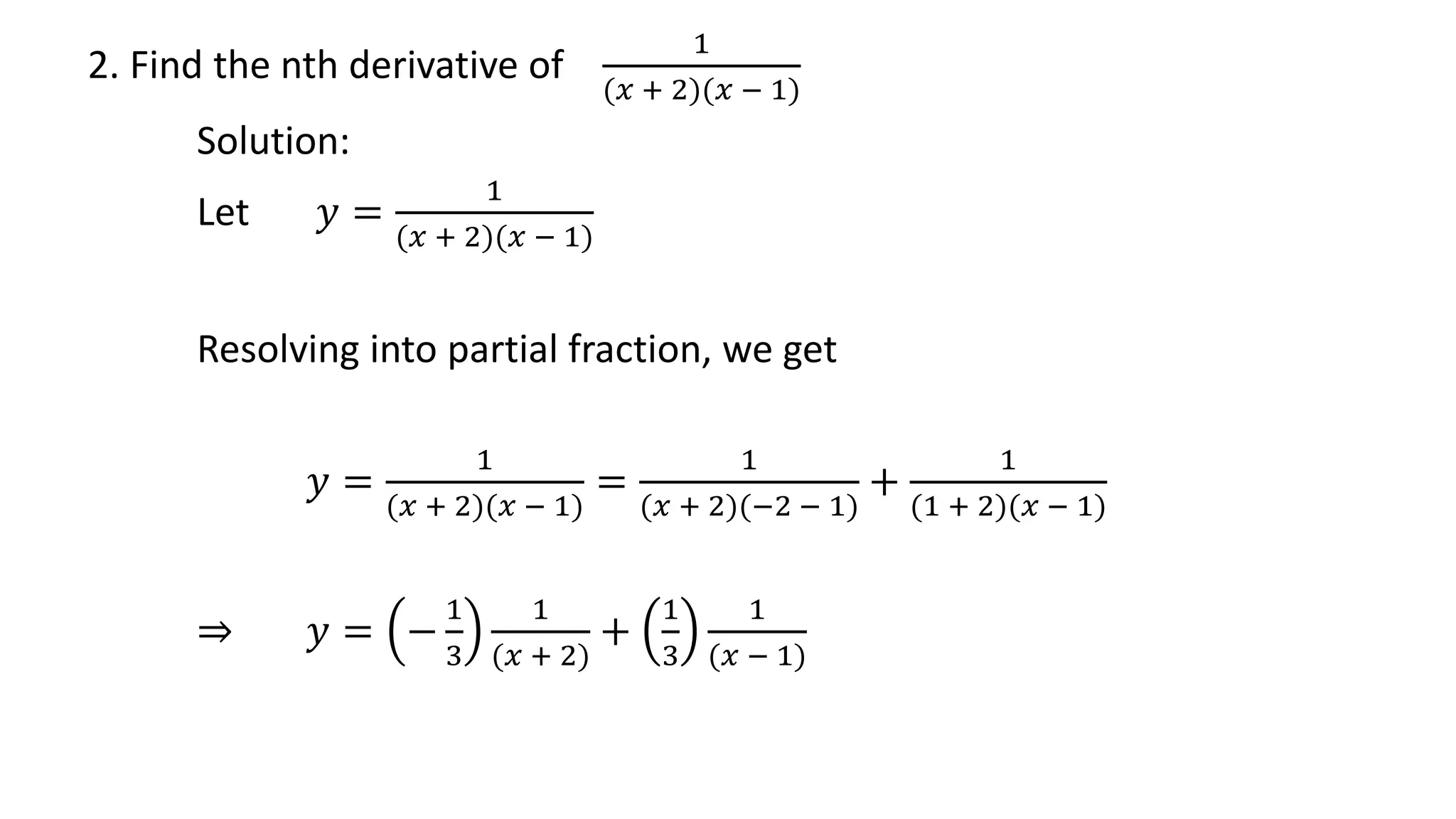
16. ⇒ 𝑦 =
1
3
1
(𝑥 − 1)
−
1
(𝑥 + 2)
∴ 𝑦𝑛 =
1
3
𝐷𝑛 1
𝑥 − 1
− 𝐷𝑛 1
𝑥 + 2
⇒ 𝑦𝑛 =
1
3
[
−1 𝑛 𝑛!
𝑥 − 1 𝑛+1 −
−1 𝑛 𝑛!
𝑥 + 2 𝑛+1]
⇒ 𝑦𝑛 =
−1 𝑛 𝑛!
3
[
1
𝑥 − 1 𝑛+1 −
1
𝑥 + 2 𝑛+1]

17. 3. Find the nth derivative of
𝑥2
𝑥 − 1 2(𝑥 − 2)
Solution:
Let 𝑦 =
𝑥2
𝑥 − 1 2(𝑥 − 2)
⇒ y =
𝑥2
𝑥 − 1 2(𝑥 − 2)
=
𝐴
𝑥 − 1
+
𝐵
𝑥 − 1 2 +
𝐶
𝑥 − 2
… … … … … (1)
⇒ 𝑥2
= 𝐴 𝑥 − 1 𝑥 − 2 + 𝐵 𝑥 − 2 + 𝐶 𝑥 − 1 2
When 𝑥 = 1, 𝐵 = −1
When 𝑥 = 2, 𝐶 = 4
When 𝑥 = 0, 2𝐴 − 2𝐵 + 𝐶 = 0 ⇒ 𝐴 = −3

18. (1) ⇒ y =
−3
𝑥 − 1
+
−1
𝑥 − 1 2 +
4
𝑥 − 2
∴ 𝑦𝑛 = −3 𝐷𝑛 1
𝑥 − 1
− 𝐷𝑛 1
𝑥 − 1 2 + 4 𝐷𝑛 1
𝑥 − 2
⇒ 𝑦𝑛 = −3
−1 𝑛 𝑛!
𝑥 − 1 𝑛+1 −
−1 𝑛 2 + 𝑛 − 1 !
𝑥 − 1 𝑛+2 + 4
−1 𝑛 𝑛!
𝑥 − 2 𝑛+1
⇒ 𝑦𝑛 = −1 𝑛𝑛!
−3
𝑥 − 1 𝑛+1 −
𝑛+1
𝑥 − 1 𝑛+2 +
4
𝑥 − 2 𝑛+1
Note: 𝐷𝑛 1
𝑎𝑥+𝑏
=
(−1)𝑛 𝑛! 𝑎𝑛
𝑎𝑥+𝑏 𝑛+1 , 𝐷𝑛 1
𝑎𝑥+𝑏 2 =
−1 𝑛 𝑛+1 ! 𝑎𝑛
1! 𝑎𝑥+𝑏 𝑛+2 ,
𝐷𝑛 1
𝑎𝑥+𝑏 3 =
−1 𝑛 𝑛+2 ! 𝑎𝑛
2! 𝑎𝑥+𝑏 𝑛+3 …

19. 4. Find the nth derivative of log
2𝑥 + 1
𝑥 − 2
Solution:
Let 𝑦 = log
2𝑥 + 1
𝑥 − 2
⇒ 𝑦 =
1
2
log
2𝑥 + 1
𝑥 − 2
(since, log 𝑎 = log(𝑎)
1
2 =
1
2
log 𝑎)
⇒ 𝑦 =
1
2
log 2𝑥 + 1 − log(𝑥 − 2)
∴ 𝑦𝑛 =
1
2
𝐷𝑛 log 2𝑥 + 1 − 𝐷𝑛 log(𝑥 − 2)

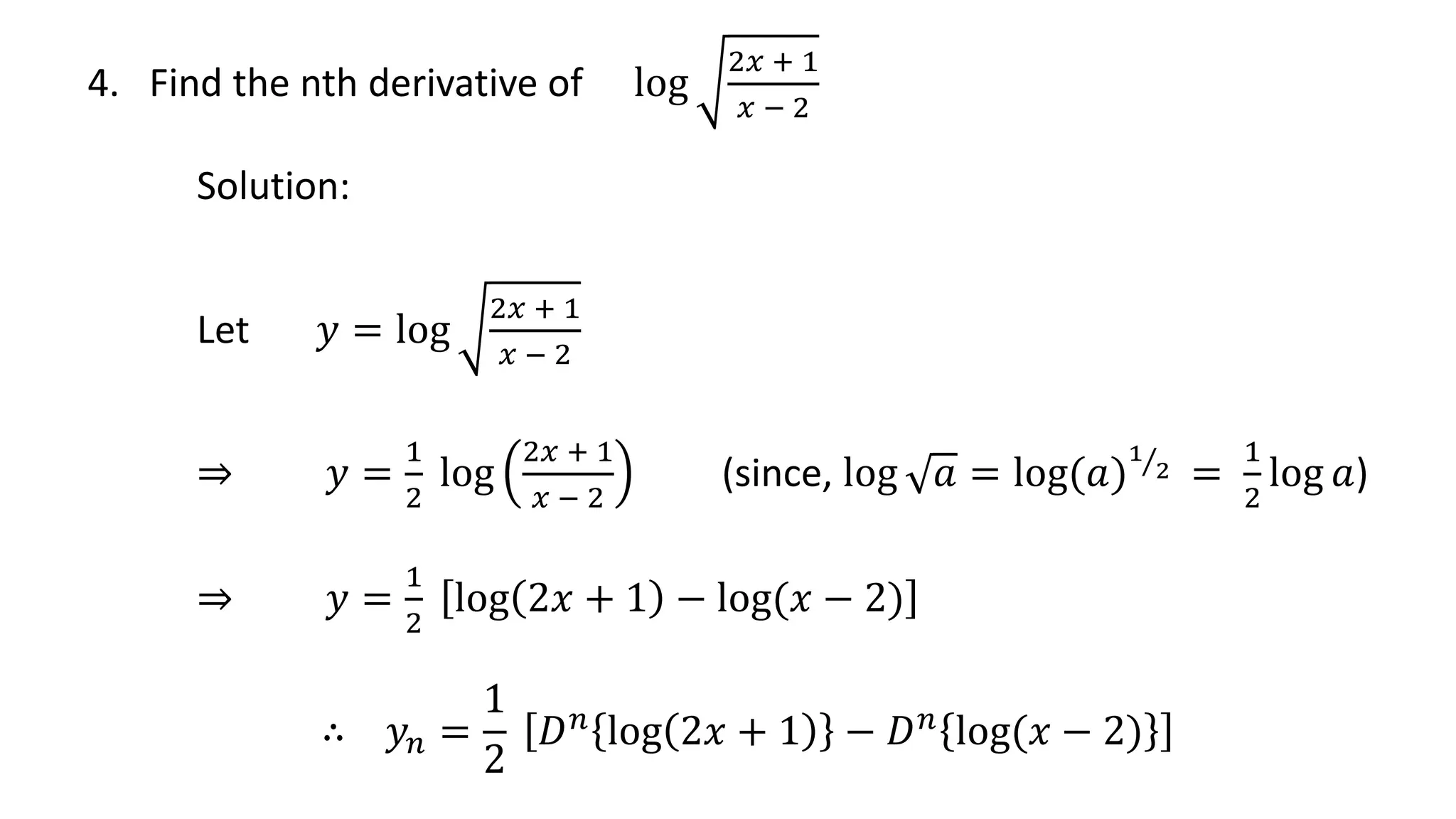
20. ⇒ 𝑦𝑛 =
1
2
[
−1 𝑛−1(𝑛−1)! 2𝑛
2𝑥 + 1 𝑛 −
−1 𝑛−1(𝑛−1)!
𝑥 − 2 𝑛 ]
⇒ 𝑦𝑛 =
−1 𝑛−1(𝑛−1)!
2
[
2𝑛
2𝑥 + 1 𝑛 −
1
𝑥 − 2 𝑛]

21. 5. Find the nth derivative of 𝑦 = log (𝑎𝑥 + 𝑥2)
Solution:
Let 𝑦 = log [𝑥 𝑎 + 𝑥 ]
⇒ 𝑦 = log 𝑥 + log(𝑎 + 𝑥) (since, log 𝑎𝑏 = log 𝑎 + log 𝑏)
∴ 𝑦𝑛 = 𝐷𝑛
log 𝑥 + 𝐷𝑛
log 𝑎 + 𝑥
⇒ 𝑦𝑛 =
−1 𝑛−1(𝑛−1)!
𝑥 𝑛 +
−1 𝑛−1(𝑛−1)!
𝑎 + 𝑥 𝑛
⇒ 𝑦𝑛 = −1 𝑛−1(𝑛 − 1)!
1
𝑥𝑛 +
1
𝑎 + 𝑥 𝑛

22. Questions for practice
Find the nth derivatives of
1. 𝑦 =
1
6𝑥2 −5𝑥+1
2. 𝑦 =
4𝑥
(𝑥 −1)2 (𝑥+1)
3. 𝑦 = log(𝑥2
− 𝑎2
)
4. 𝑦 = log(𝑎𝑥 − 𝑥2)

23. 1. Find the nth derivative of
1
6𝑥2 −5𝑥+1
Solution:
Let 𝑦 =
1
6𝑥2 −5𝑥+1
⇒ 𝑦 =
1
2𝑥−1 (3𝑥−1)
Resolving into partial fraction, we get
𝑦 =
1
2𝑥−1 (3𝑥−1)
=
𝐴
(2𝑥 −1)
+
𝐵
(3𝑥 − 1)
… … … … … … (1)
⇒ 1 = 𝐴 3𝑥 − 1 + 𝐵 2𝑥 − 1
When 𝑥 =
1
3
, 𝐵
2
3
− 1 = 1 ⇒
−1
3
𝐵 = 1 ⇒ 𝐵 = −3
When 𝑥 =
1
, 𝐴
3
− 1 = 1 ⇒
1
𝐴 = 1 ⇒ 𝐴 = 2

24. ∴ (1) ⇒ 𝑦 ==
2
(2𝑥 −1)
+
−3
(3𝑥 − 1)
∴ 𝑦𝑛 = 2𝐷𝑛 1
2𝑥 −1
− 3𝐷𝑛 1
3𝑥− 1
⇒ 𝑦𝑛 = 2
−1 𝑛 𝑛! 2𝑛
2𝑥 −1 𝑛+1 − 3
−1 𝑛 𝑛! 3𝑛
3𝑥 − 1 𝑛+1
⇒ 𝑦𝑛 = −1 𝑛 𝑛!
2𝑛+1
2𝑥 −1 𝑛+1 −
3𝑛+1
3𝑥 − 1 𝑛+1

25. 2. Find the nth derivative of
4𝑥
(𝑥 −1)2 (𝑥+1)
Solution:
Let 𝑦 =
4𝑥
(𝑥 −1)2 (𝑥+1)
⇒ y =
4𝑥
(𝑥 −1)2 (𝑥+1)
=
𝐴
𝑥 − 1
+
𝐵
𝑥 − 1 2 +
𝐶
𝑥 + 1
… … … … … (1)
⇒ 4𝑥 = 𝐴 𝑥 − 1 𝑥 + 1 + 𝐵 𝑥 + 1 + 𝐶 𝑥 − 1 2
When 𝑥 = 1, 𝐵 = 2
When 𝑥 = −1, 𝐶 = −1
When 𝑥 = 0, −𝐴 + 𝐵 + 𝐶 = 0 ⇒ 𝐴 = 1

26. (1) ⇒ y =
1
𝑥 − 1
+
2
𝑥 − 1 2 −
1
𝑥 + 1
∴ 𝑦𝑛 = 𝐷𝑛 1
𝑥 − 1
+ 2𝐷𝑛 1
𝑥 − 1 2 − 𝐷𝑛 1
𝑥 + 1
⇒ 𝑦𝑛 =
−1 𝑛 𝑛!
𝑥 − 1 𝑛+1 + 2
−1 𝑛 2 + 𝑛 − 1 !
𝑥 − 1 𝑛+2 −
−1 𝑛 𝑛!
𝑥+1 𝑛+1
⇒ 𝑦𝑛 = −1 𝑛
𝑛!
1
𝑥 − 1 𝑛+1 + 2
𝑛+1
𝑥 − 1 𝑛+2 −
1
𝑥 + 1 𝑛+1

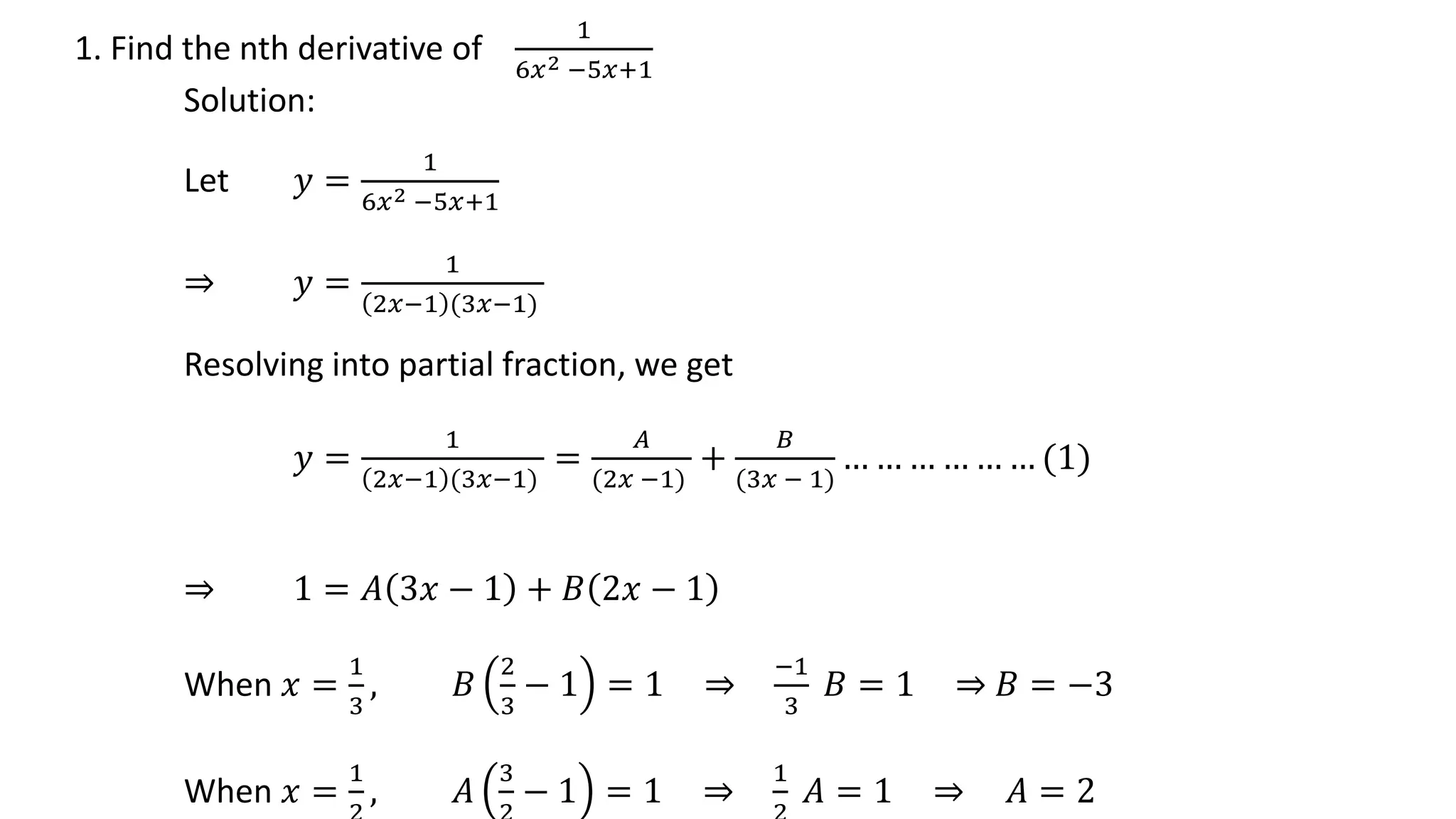
27. 3. Find the nth derivative of 𝑦 = log(𝑥2
− 𝑎2
)
Solution:
Let 𝑦 = log(𝑥2 − 𝑎2)
⇒ 𝑦 = log [(𝑥 + 𝑎) (𝑥 − 𝑎)]
⇒ 𝑦 = log (𝑥 + 𝑎) + log (𝑥 − 𝑎)
∴ 𝑦𝑛 = 𝐷𝑛 log(𝑥 + 𝑎) + 𝐷𝑛 log 𝑥 − 𝑎
⇒ 𝑦𝑛 =
−1 𝑛−1(𝑛−1)!
𝑥 + 𝑎 𝑛 +
−1 𝑛−1(𝑛−1)!
𝑥 − 𝑎 𝑛
⇒ 𝑦𝑛 = −1 𝑛−1
(𝑛 − 1)!
1
(𝑥+𝑎)𝑛 +
1
𝑥 − 𝑎 𝑛

28. 4. Find the nth derivative of 𝑦 = log(𝑎𝑥 − 𝑥2
)
Solution:
Let y = log(𝑎𝑥 − 𝑥2)
⇒ 𝑦 = log [𝑥 𝑎 − 𝑥 ]
⇒ 𝑦 = log 𝑥 + log(𝑎 − 𝑥)
∴ 𝑦𝑛 = 𝐷𝑛 log 𝑥 + 𝐷𝑛 log 𝑎 − 𝑥
⇒ 𝑦𝑛 =
−1 𝑛−1(𝑛−1)!
𝑥 𝑛 +
−1 𝑛−1 𝑛−1 ! −1 𝑛
𝑎 − 𝑥 𝑛
⇒ 𝑦𝑛 = −1 𝑛−1(𝑛 − 1)!
1
𝑥𝑛 +
−1 𝑛
𝑎 − 𝑥 𝑛