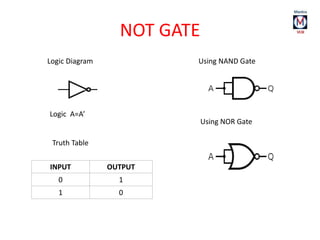
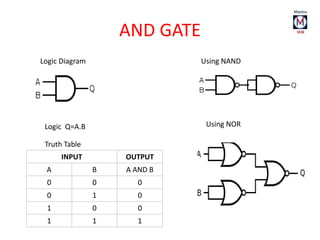
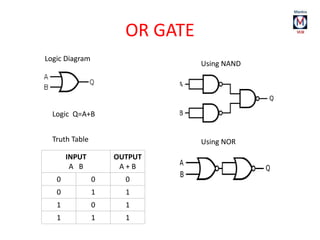
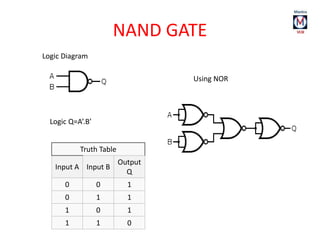
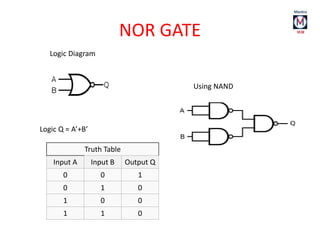
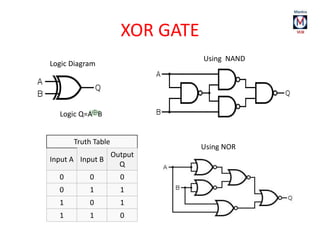
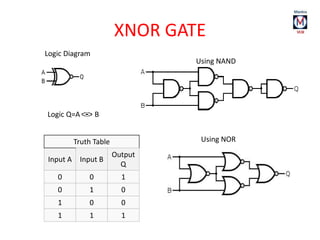
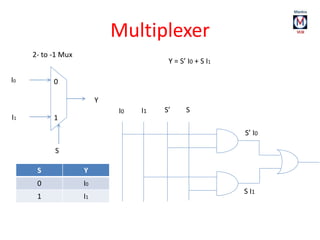
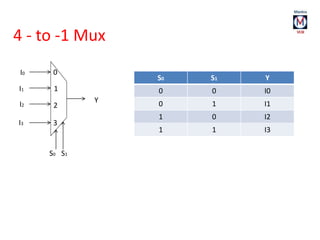
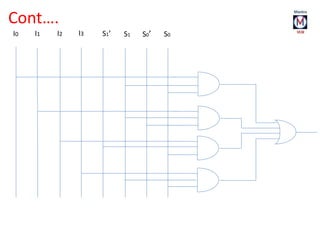
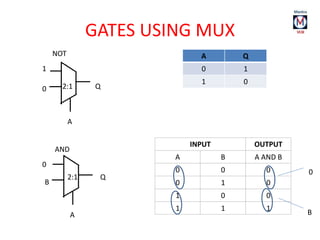
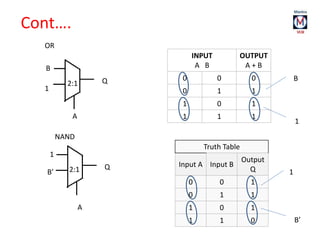
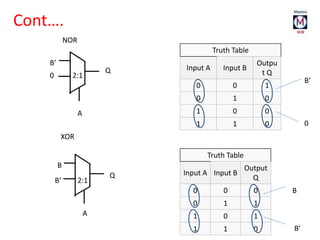
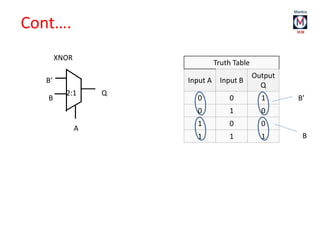
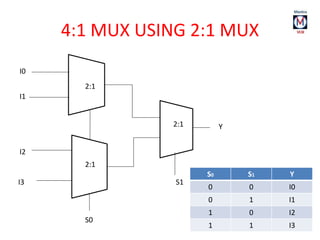
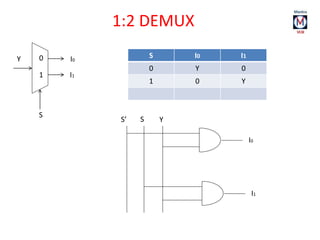
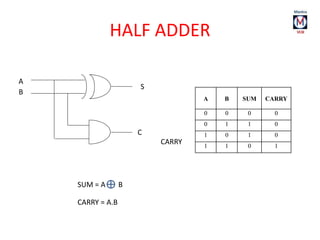
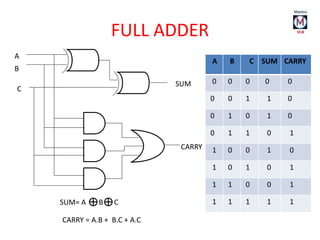
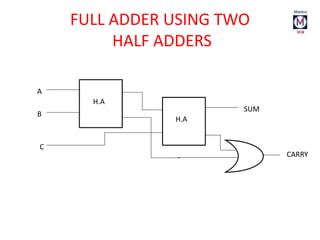
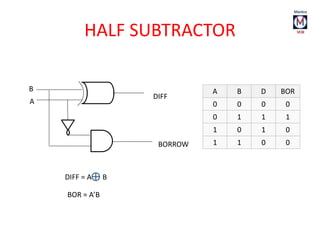
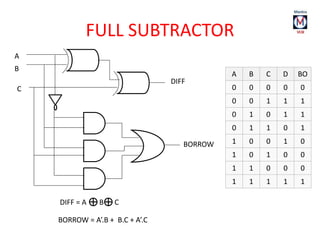
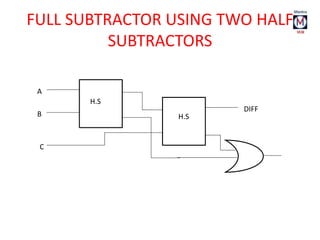
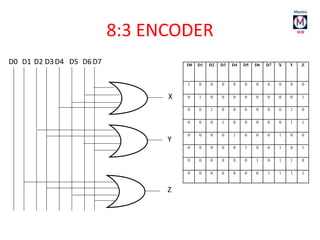
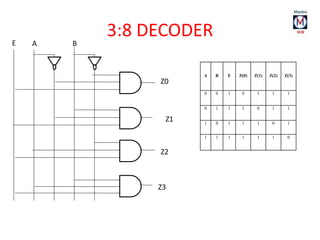
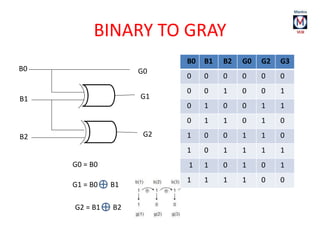
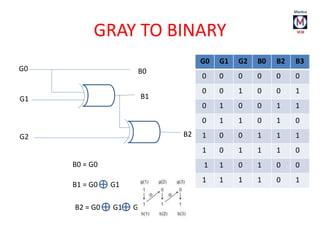
The document summarizes basic digital logic gates and components including NOT, AND, OR, NAND, NOR, XOR, XNOR gates. It also discusses multiplexers, demultiplexers, half/full adders, half/full subtractors, encoders, decoders, and conversions between binary and gray codes.

1. Basic Logic of Digital Electronics

2. NOT GATE
Logic Diagram
INPUT OUTPUT
0 1
1 0
Truth Table
Using NAND Gate
Using NOR Gate
Logic A=A’

3. AND GATE
Logic Diagram
Logic Q=A.B
Using NAND
INPUT OUTPUT
A B A AND B
0 0 0
0 1 0
1 0 0
1 1 1
Truth Table
Using NOR

4. OR GATE
Logic Diagram
Using NAND
Using NOR
INPUT
A B
OUTPUT
A + B
0 0 0
0 1 1
1 0 1
1 1 1
Truth Table
Logic Q=A+B

5. NAND GATE
Logic Diagram
Using NOR
Logic Q=A’.B’
Truth Table
Input A Input B
Output
Q
0 0 1
0 1 1
1 0 1
1 1 0

6. NOR GATE
Logic Diagram
Using NAND
Logic Q = A’+B’
Truth Table
Input A Input B Output Q
0 0 1
0 1 0
1 0 0
1 1 0

7. XOR GATE
Logic Diagram
Truth Table
Input A Input B
Output
Q
0 0 0
0 1 1
1 0 1
1 1 0
Using NAND
Using NOR
Logic Q=A B

8. XNOR GATE
Logic Diagram
Using NAND
Using NORTruth Table
Input A Input B
Output
Q
0 0 1
0 1 0
1 0 0
1 1 1
Logic Q=A B

9. Multiplexer
I0
I1
Y
S
0
1
2- to -1 Mux
S Y
0 I0
1 I1
Y = S’ I0 + S I1
I0 I1 S’ S
S’ I0
S I1

10. Y
0
1
4 - to -1 Mux
S0 S1
2
3
I0
I1
I2
I3
S0 S1 Y
0 0 I0
0 1 I1
1 0 I2
1 1 I3

11. I0 I1 S1’ S1I3I2 S0’ S0
Cont….

12. GATES USING MUX
NOT
1
0
A
Q
AND
INPUT OUTPUT
A B A AND B
0 0 0
0 1 0
1 0 0
1 1 1
0
0
B
B
A
Q
2:1
2:1
A Q
0 1
1 0

13. INPUT
A B
OUTPUT
A + B
0 0 0
0 1 1
1 0 1
1 1 1
Truth Table
Input A Input B
Output
Q
0 0 1
0 1 1
1 0 1
1 1 0
B
1
1
B’
A
A
B
1
1
B’
OR
NAND
Q
Q
2:1
2:1
Cont….

14. Truth Table
Input A Input B
Outpu
t Q
0 0 1
0 1 0
1 0 0
1 1 0
Truth Table
Input A Input B
Output
Q
0 0 0
0 1 1
1 0 1
1 1 0
B’
0
B
B’
Q
Q
A
A
B’
0
B
B’
NOR
XOR
2:1
2:1
Cont….

15. Truth Table
Input A Input B
Output
Q
0 0 1
0 1 0
1 0 0
1 1 1
B’
B
B’
B
A
Q
XNOR
2:1
Cont….

16. 4:1 MUX USING 2:1 MUX
2:1
2:1
2:1
I0
I1
I2
I3
S0
S1
Y
S0 S1 Y
0 0 I0
0 1 I1
1 0 I2
1 1 I3

17. I0
I11
0Y S I0 I1
0 Y 0
1 0 Y
S
I0
YS’
I1
S
1:2 DEMUX

18. HALF ADDER
A B SUM CARRY
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
CARRY
SUM = A B
CARRY = A.B
A
B
S
C

19. FULL ADDER
SUM
CARRY
A
B
C
A B C SUM CARRY
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1SUM= A B C
CARRY = A.B + B.C + A.C

20. FULL ADDER USING TWO
HALF ADDERS
H.A
H.A
A
B
C
SUM
CARRY

21. HALF SUBTRACTOR
DIFF
BORROW
B
A
A B D BOR
0 0 0 0
0 1 1 1
1 0 1 0
1 1 0 0
DIFF = A B
BOR = A’B

22. FULL SUBTRACTOR
A
B
C
DIFF = A B C
BORROW = A’.B + B.C + A’.C
A B C D BO
0 0 0 0 0
0 0 1 1 1
0 1 0 1 1
0 1 1 0 1
1 0 0 1 0
1 0 1 0 0
1 1 0 0 0
1 1 1 1 1
DIFF
BORROW

23. FULL SUBTRACTOR USING TWO HALF
SUBTRACTORS
H.S
H.S
A
B
C
DIFF

24. 8:3 ENCODER
D0 D1 D2 D3 D4 D5 D6 D7 X Y Z
1 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 1 1
0 0 0 0 1 0 0 0 1 0 0
0 0 0 0 0 1 0 0 1 0 1
0 0 0 0 0 0 1 0 1 1 0
0 0 0 0 0 0 0 1 1 1 1
D0 D1 D2 D3D4 D5 D6D7
X
Y
Z

25. 3:8 DECODERE A B
Z0
Z1
Z2
Z3
A B E Z(0) Z(1) Z(2) Z(3)
0 0 1 0 1 1 1
0 1 1 1 0 1 1
1 0 1 1 1 0 1
1 1 1 1 1 1 0

26. BINARY TO GRAY
G0
G1
G2
B0 B1 B2 G0 G2 G3
0 0 0 0 0 0
0 0 1 0 0 1
0 1 0 0 1 1
0 1 1 0 1 0
1 0 0 1 1 0
1 0 1 1 1 1
1 1 0 1 0 1
1 1 1 1 0 0
B0
B1
B2
G0 = B0
G1 = B0 B1
G2 = B1 B2

27. GRAY TO BINARY
B0
B1
B2
G0
G1
G2
G0 G1 G2 B0 B2 B3
0 0 0 0 0 0
0 0 1 0 0 1
0 1 0 0 1 1
0 1 1 0 1 0
1 0 0 1 1 1
1 0 1 1 1 0
1 1 0 1 0 0
1 1 1 1 0 1
B0 = G0
B1 = G0 G1
B2 = G0 G1 G2