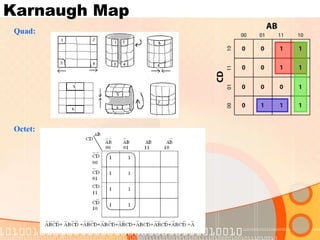
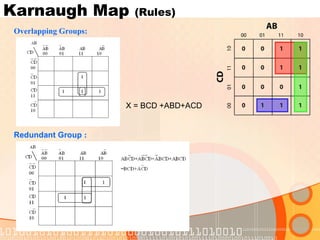
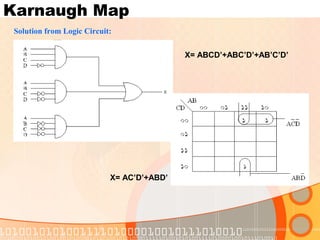
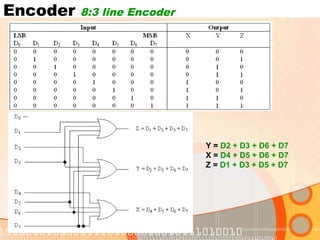
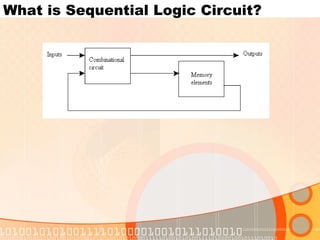
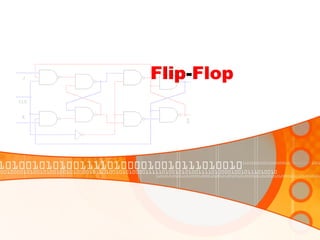
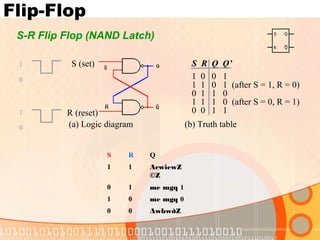
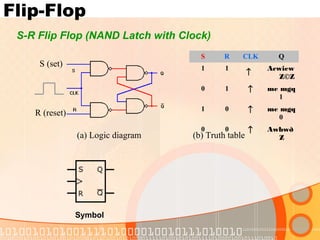
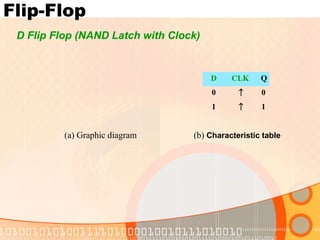
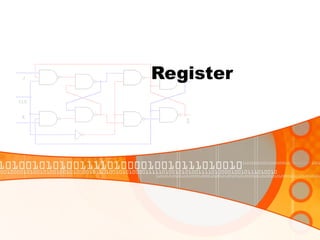
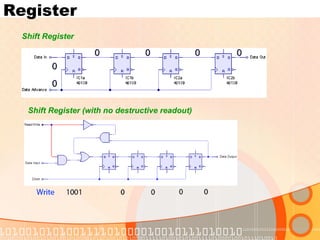
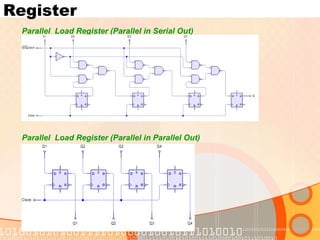
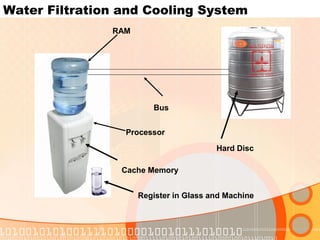
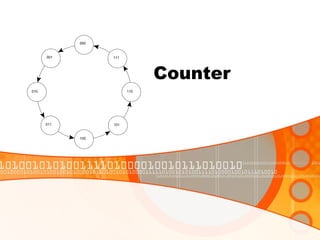
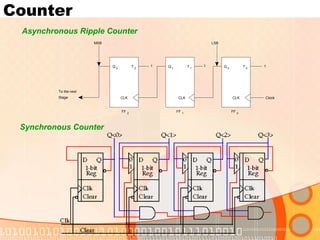
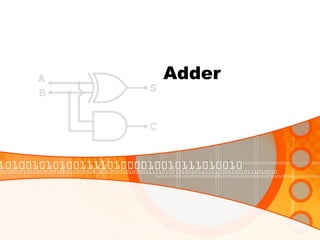
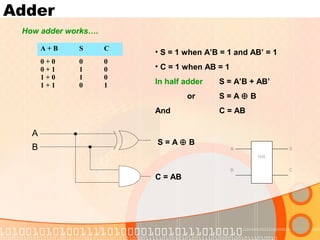
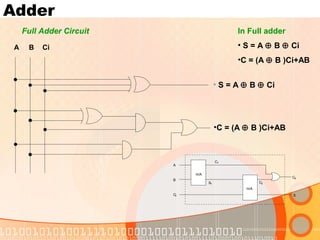
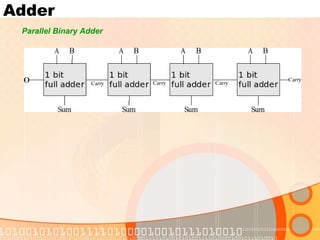
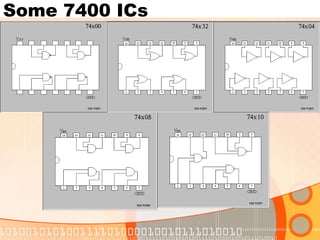
The document provides an overview of the topics covered in a digital logic design course, including Boolean algebra, logic gates, Karnaugh maps, encoders, decoders, flip-flops, registers, counters, adders, and signed number representation. The course syllabus covers basic concepts in digital logic like logic functions, logic gates, sequential logic circuits, and how to design combinational and sequential logic circuits using logic gates.

1. Digital Logic Design
(HSC curriculum based)
M Rashidul Hasan
admin@systechdigital.com

2. Where You Get…

3. Syllabus
• Boolean Algebra
• Truth Table
• De-Morgan’s Law
• Logic Functions
• Logic Gates
• Karnaugh Map
• Decoder
• Encoder
• Sequential Logic Circuit
• Flip-Flop
• Register
• Counter
• Adder
• Signed Number

4. Let’s Play a Game

5. Can I Guess Your Age?

6. Can you guess how
this game works???

7. Can you solve this now?

8. Boolean Algebra

9. Boolean Operators
• AND
• Result TRUE if and only if both
input operands are true
• C = A  B
• INCLUSIVE-OR
• Result TRUE if any input operands
are true
• C = A + B
A B C
0 0 0
0 1 0
1 0 0
1 1 1
A B C
0 0 0
0 1 1
1 0 1
1 1 1

10. Boolean Operators (Continued)
• NOT
• Result TRUE if single input value is
FALSE
• C = A
A C
0 1
1 0

11. Boolean Theorems

12. Boolean Theorems (Explanations)

13. Truth Table
A B AB A+AB
0
1
0
1
0
0
1
1
0
0
0
1
0
1
0
1
Example 1 : A+A.B = A
Example 1 : A + A’B = A+B
A A’ B A’B A+A’B A+B
0
1
0
1
1
0
1
0
0
0
1
1
0
0
1
0
0
1
1
1
0
1
1
1
0 + 0 = 0 . . . . . . . . . 1
1 + 0 = 1 . . . . . . . . . 2
0 + 1 = 1 . . . . . . . . . 3
1 + 1 = 1 . . . . . . . . . 4
0 . 0 = 0
1 . 0 = 0
0 . 1 = 0
1 . 1 = 1
Proof Using Truth Table

14. De Morgan's Theorem
0 + 0 = 0 . . . . . . . . . 1
1 + 0 = 1 . . . . . . . . . 2
0 + 1 = 1 . . . . . . . . . 3
1 + 1 = 1 . . . . . . . . . 4
0 . 0 = 0
1 . 0 = 0
0 . 1 = 0
1 . 1 = 1
(A + B) = A . B - - - - - - - - (1)
(A . B) = A + B - - - - - - - (2)
A A B B A + B A + B A . B A . B A . B A + B
0
1
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
1
1
1
0
0
0
0
0
0
1
1
1
1
0
1
0
0
0
1
1
1
0
Proof:

15. Logic Gates

16. Logic Gates
• Gates or logical gates
• Integrated circuits
constructed from
transistor switches and
other electronic
components
• VLSI: very large-scale
integration
NOT ORAND
NMOS

17. Logic Gates
• Making AND Gate

18. Logic Gates
AND
AND Gate
A B C
0 0 0
0 1 0
1 0 0
1 1 1
A
C
X = ABCB
Input Output
A B C X=ABC
0
0
0
1
1
0
1
1
0
0
1
0
1
1
0
1
0
1
1
0
0
1
1
1
0
0
0
0
0
0
0
1

19. Logic Gates
OR Gate
A B C
0 0 0
0 1 1
1 0 1
1 1 1
OR
A
B X = A + B + C
C
Input Output
A B C X=A+B+C
0
0
0
0
1
1
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
0
0
1
0
1
1
1
1
1
1
1
A B X

20. Logic Gates
NOT Gate
A C
0 1
1 0
NOT
Input Output
A X
0
1
0
1
Buffer Gate

21. Other Combined Logic Gates
NAND Gate
A
B
X = AB
A
B
X = AB
AB
Input Output
A B X
0
1
0
1
0
0
1
1
1
1
1
0
NOR Gate
Input Output
A B X
0
1
0
1
0
0
1
1
1
0
0
0
A
B
X = A + B
A
B
X = A + B
A+B

22. Other Combined Logic Gates
XOR Gate
XNOR Gate
X = A + B = A'B + AB'
A
B
Input Output
A B X
0
0
1
1
0
1
0
1
0
1
1
0
X = A + B = AB + BA
Input Output
A B X
0
1
0
1
0
0
1
1
1
0
0
1

23. All Logic Gates and IEEE standards

24. What is the meaning
of ASCII???

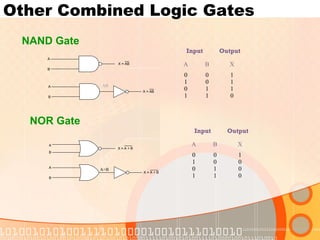
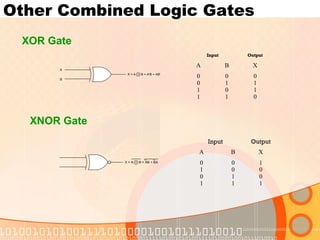
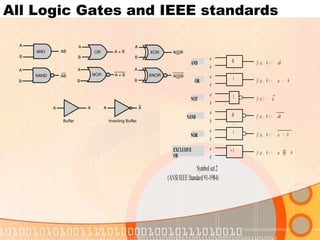
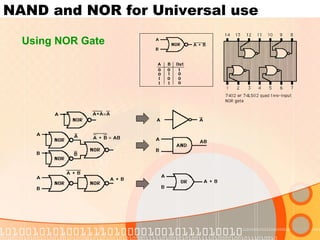
25. NAND and NOR for Universal use
Using NAND Gate
[wW-giM¨v‡bi mÎvbymv‡i A.B
= A + B ]

26. NAND and NOR for Universal use
Using NOR Gate

27. Karnaugh MapY
1 0 0 1
0 1 0 0
0 1 0 0
X
W
1 0 0 1
Z

28. Do you know the other
name of Karnaugh
Map???

29. Karnaugh Map
Number of boxes will
be 2n
where n is
number of operator

30. Karnaugh Map
Example 1:
Consider the following map. The function plotted is: Z = f(A,B) = AB’ + AB
Using algebraic simplification,
Z = AB’ + AB
Z = A( B’+ B)
Z = A
Example 2:
Consider the expression Z = f(A,B) = A’B’ + AB’+A’B plotted on the Karnaugh map:
Hence the simplified answer is Z = A’ +B’

31. Karnaugh Map
Minterm:
Pair:
Number of term will
be 2n
where n is
number of operator
BC'D'
F(A, B, C) = Σ (3, 15, 6, 2, 7, 11, 8)

32. Karnaugh Map
Quad:
Octet:

33. Karnaugh Map (Rules)
Overlapping Groups:
Redundant Group :
X = BCD +ABD+ACD

34. Karnaugh Map
Solution from Logic Circuit:
X= ABCD’+ABC’D’+AB’C’D’
X= AC’D’+ABD’

35. Decoder & Encoder

36. Decoder
• 3:8 line Decoder

37. Decoder
• 3:8 line Decoder Circuit

38. Encoder 8:3 line Encoder
Y = D2 + D3 + D6 + D7
X = D4 + D5 + D6 + D7
Z = D1 + D3 + D5 + D7

39. Can you say a computer
peripheral name which is
used for external data
encoding and decoding ???

40. Sequential Logic Circuit

41. What is Sequential Logic Circuit?

42. Flip-FlopFlip Flop

43. Flip-Flop
S-R Flip Flop (NAND Latch)
1
0
1
0
S (set)
R (reset)
(a) Logic diagram (b) Truth table
S R Q Q’
1 0 0 1
1 1 0 1 (after S = 1, R = 0)
0 1 1 0
1 1 1 0 (after S = 0, R = 1)
0 0 1 1
S R Q
1 1 AcwiewZ
©Z
0 1 me mgq 1
1 0 me mgq 0
0 0 AwbwðZ

44. Flip-Flop
S-R Flip Flop (NAND Latch with Clock)
S (set)
R (reset)
(a) Logic diagram (b) Truth table
S R CLK Q
1 1
↑
Acwiew
Z©Z
0 1 ↑ me mgq
1
1 0 ↑ me mgq
0
0 0 ↑ Awbwð
Z
Symbol

45. Flip-Flop
D CLK Q
0 ↑ 0
1 ↑ 1
D Flip Flop (NAND Latch with Clock)
(a) Graphic diagram (b) Characteristic table

46. Flip-Flop
JK Flip Flop
(a) Graphic diagram
(b) Characteristic table
J K CLK Q
0 0 ↑ Q0
Acwiew
Z©Z
0 1 ↑ memgq 0
1 0 ↑ memgq|
1 1 ↑ Q0
(Toggle)

47. Flip-Flop
T CLK Q
0 ↑ Q0
1 ↑ Q0
(Toggle)
T Flip Flop
(a) Graphic diagram
(b) Characteristic table

48. Register

49. Can you say what is
resistor ???

50. Register
†iwR÷vi wK?
†iwR÷vi n‡jv GK cÖKvi †g‡gvwi wWfvBm hv KZ¸‡jv weU‡K aviY
K‡i _v‡K| GwU GK¸”Q wd¬c-d¬c-Gi mgš^‡q MwVZ, †hLv‡b
cÖ‡Z¨KwU wd¬c-d¬c GKwU K‡i evBbvwi weU aviY K‡i _v‡K|
myZivs, n-weU †iwR÷v‡i n msL¨K wd¬c-d¬c _v‡K Ges GUv n-weU-Gi
†h‡Kvb evBbvwi Z_¨‡K aviY Ki‡Z cv‡i| wd¬c-d¬c QvovI †iwR÷v‡i
Kw¤^‡bkbvj (Combinational) †MBU _vK‡Z cv‡i, †hUv †iwR÷v‡ii
wfZ‡i Af¨š—ixY Feedback Path ˆZwi Ki‡Z A_ev wewfbœ cÖKvi WvUv
cÖ‡mwms‡qi Kv‡R e¨eüZ nq| e¨vcK A‡_© †iwR÷vi n‡jv KZ¸‡jv wd¬c-
d¬c-Gi mgš^‡q MwVZ mvwK©U hv evBbvwi Z_¨‡K msi¶Y/aviY K‡i
_v‡K|
AX, BX, CX, DX, EX Ges SX

51. Register
Shift Register
Shift Register (with no destructive readout)

52. Register
Parallel Load Register (Parallel in Serial Out)
Parallel Load Register (Parallel in Parallel Out)

53. Explanation: How Computer Memory Works

54. Water Filtration and Cooling System
RAM
Hard Disc
Cache Memory
Register in Glass and Machine
Bus
Processor

55. Do you know what does
mean by DIMM
RAM???

56. Counter
000
100
101
110
111001
010
011

57. Counter
Usage of Counter
1. To count digital event
2. To provide timing signal
3. To control operations of digital circuits
Kind of Counters
1. Asynchronous Counter
1. Ripple up counter
2. Ripple down counter
2. Synchronous Counter

58. Counter
Asynchronous Ripple Counter
MSB LSB
ClockCLK
FF 0
FF 1
FF 2
CLKCLK
Q 2
T 2
Q 1
T 1
Q 0
T 0
1 1 1
To the next
Stage
Synchronous Counter

59. Can you say an
instrument name where
digital counter used???

60. Adder

61. Adder
How adder works….
A + B S C
0 + 0
0 + 1
1 + 0
1 + 1
0
1
1
0
0
0
0
1
• S = 1 when A’B = 1 and AB’ = 1
• C = 1 when AB = 1
In half adder S = A’B + AB’
or S = A ⊕ B
And C = AB
A
B
S = A ⊕ B
C = AB
H/A
A
B
S
C

62. Adder
Full Adder
Input Outputs
A B Ci S Co
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0
1
1
0
1
0
0
1
0
0
0
1
0
1
1
1
In Full adder
• S = A’B’Ci+A’BCi’+AB’Ci’+ABCi
•C =A’BCi+AB’Ci+ABCi’+ABCi

63. Adder
Full Adder Circuit In Full adder
• S = A ⊕ B ⊕ Ci
•C = (A ⊕ B )Ci+AB
A B Ci
• S = A ⊕ B ⊕ Ci
•C = (A ⊕ B )Ci+AB
A
H/A
H/A
B
Ci
C1
C2
Co
S1
S

64. Adder
Parallel Binary Adder

65. Signed Number

66. Signed Representation

67. Some 7400 ICs

68. References
Computer Books
• Computer Fundamentals – Dr. Lutfar Rahman & Dr.Alamgir Kabir
•Computer Fundamentals – Malvino
•Computer Fundamentals – B Ram
Circuit Design & Simulation Software
•Electronics Work Bench
•Tina Pro
•Circuits Works
•MS Visio 2003
•Electronic Circuit Simulator
•Karnaugh Minimizer