Downloaded 60 times
![16-bit Cascading Comparator
A B
AGTBin
AEQBin
ALTBin
4 4
AGTBout
AEQBout
ALTBout
A[3:0] B[3:0]
A B
AGTBin
AEQBin
ALTBin
4 4
AGTBout
AEQBout
ALTBout
A[7:4] B[7:4]
A B
AGTBin
AEQBin
ALTBin
4 4
AGTBout
AEQBout
ALTBout
A[11:8] B[11:8]
A B
AGTBin
AEQBin
ALTBin
4 4
AGTBout
AEQBout
ALTBout
A[15:12] B[15:12]
0
1
0
A>B
A<B
A=B
B[15:0]
A[15:0]](https://image.slidesharecdn.com/lec11-dec-150829105857-lva1-app6892/85/Lec11-Intro-to-Computer-Engineering-by-Hsien-Hsin-Sean-Lee-Georgia-Tech-Decoder-Encoder-and-Comparator-39-320.jpg)
Uploaded byHsien-Hsin Sean Lee, Ph.D.
Lec11 Intro to Computer Engineering by Hsien-Hsin Sean Lee Georgia Tech -- Decoder, Encoder and Comparator
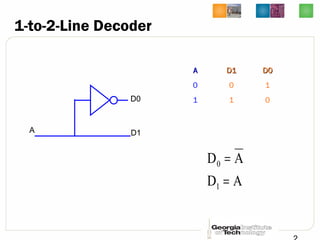
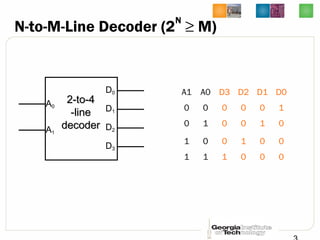
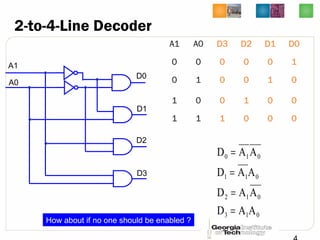
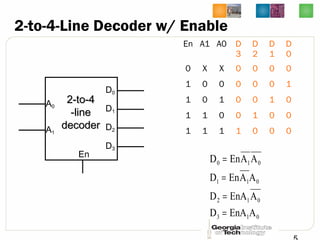
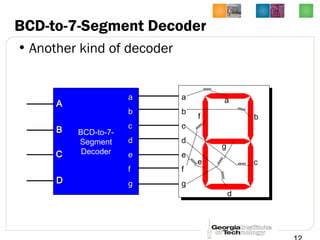
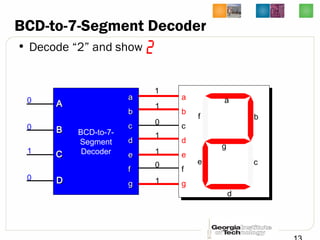
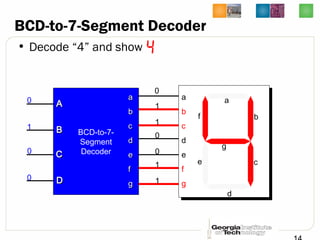
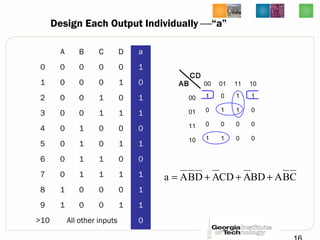
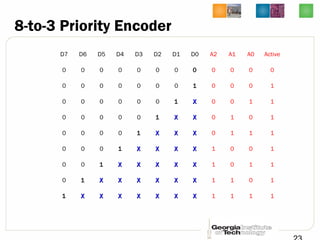
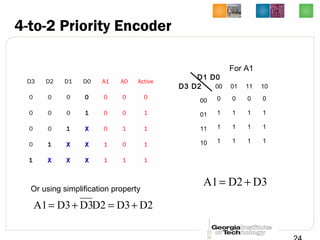
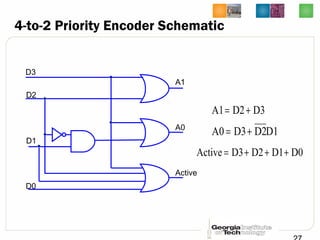
This document discusses different types of decoders and encoders used in digital logic circuits. It begins by explaining 1-to-2 line, N-to-M line, and 2-to-4 line decoders. It then describes decoders with enables and how to implement logic functions using decoders. The document also covers BCD-to-7 segment decoders and designing the outputs individually. Finally, it summarizes M-to-N line encoders and provides examples of 4-to-2 and 8-to-3 encoders as well as priority encoders.
More Related Content
Similar to Lec11 Intro to Computer Engineering by Hsien-Hsin Sean Lee Georgia Tech -- Decoder, Encoder and Comparator
![Analysis_Design_Procedures_with_Diagrams[1].pptx](https://cdn.slidesharecdn.com/ss_thumbnails/analysisdesignprocedureswithdiagrams1-250902110500-deeb2e09-thumbnail.jpg?width=640&height=640&fit=bounds)
![Analysis_Design_Procedures_with_Diagrams[1].pptx](https://cdn.slidesharecdn.com/ss_thumbnails/analysisdesignprocedureswithdiagrams1-250902110906-778fd956-thumbnail.jpg?width=640&height=640&fit=bounds)
Lec11 Intro to Computer Engineering by Hsien-Hsin Sean Lee Georgia Tech -- Decoder, Encoder and Comparator
- 1. ECE2030 Introduction to ComputerEngineering Lecture 11: Building Blocks for Combinational Logic (2) Decoders/Encoders, Comparators Prof. Hsien-Hsin Sean LeeProf. Hsien-Hsin Sean Lee School of Electrical and Computer EngineeringSchool of Electrical and Computer Engineering Georgia TechGeorgia Tech
- 2. 1-to-2-Line Decoder AD AD 1 0 = = AA D1D1D0D0 0 0 1 1 1 0D0 D1A
- 3. N-to-M-Line Decoder (2 N ≥M) A1 A0 D3 D2 D1 D0 0 0 0 0 0 1 0 1 0 0 1 0 1 0 0 1 0 0 1 1 1 0 0 0 D0 D1 D2 D3 2-to-42-to-4 -line-line decoderdecoder A0 A1
- 4. 2-to-4-Line Decoder A1 A0D3 D2 D1 D0 0 0 0 0 0 1 0 1 0 0 1 0 1 0 0 1 0 0 1 1 1 0 0 0 013 012 011 010 AAD AAD AAD AAD = = = = How about if no one should be enabled ? A1 A0 D0 D1 D2 D3
- 5. 2-to-4-Line Decoder w/Enable En A1 A0 D 3 D 2 D 1 D 0 0 X X 0 0 0 0 1 0 0 0 0 0 1 1 0 1 0 0 1 0 1 1 0 0 1 0 0 1 1 1 1 0 0 0 013 012 011 010 AEnAD AEnAD AAEnD AAEnD = = = = D0 D1 D2 D3 2-to-42-to-4 -line-line decoderdecoder A0 A1 En
- 6. 2-to-4-Line Decoder w/Enable En A1 A0 D 3 D 2 D 1 D 0 0 X X 0 0 0 0 1 0 0 0 0 0 1 1 0 1 0 0 1 0 1 1 0 0 1 0 0 1 1 1 1 0 0 0 013 012 011 010 AEnAD AEnAD AAEnD AAEnD = = = = A1 A0 D0 D1 D2 D3 En
- 7. 3-to-8-Line Decoder A2 A1A0 D 7 D 6 D 5 D 4 D 3 D 2 D 1 D 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 Truth Table
- 8. 3-to-8-Line Decoder A2 A1A0 D 7 D 6 D 5 D 4 D 3 D 2 D 1 D 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 Truth Table
- 9. 3-to-8-Line Decoder A2 A1A0 D7 D6 D5 D4 D3 D2 D1 D0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 D0 D1 D2 D3 2-to-42-to-4 -line-line decoderdecoder A0 A1 En D0 D1 D2 D3 D0 D1 D2 D3 2-to-42-to-4 -line-line decoderdecoder A0 A1 En D4 D5 D6 D7 A0 A1 A2
- 10. Implementing Logic w/Decoder D0 D1 D2 D3 3-to-83-to-8 -line-line decoderdecoder A0 A1 A2 D4 D5 D6 D7 ∏ ∑ = = 5,7)M(0,1,2,3,Z)Y,F2(X, m(1,2,6,7)Z)Y,F1(X, XX YY ZZ F1F1 F2F2
- 11. BCD-to-7- Segment Decoder BCD-to-7-Segment Decoder • Anotherkind of decoder a b c d e f g aa bb cc dd ee ff gg AA BB CC DD
- 12. BCD-to-7- Segment Decoder BCD-to-7-Segment Decoder • Anotherkind of decoder a b c d e f g aa bb cc dd ee ff gg AA BB CC DD a b c d e g f
- 13. BCD-to-7- Segment Decoder BCD-to-7-Segment Decoder • Decode“2” and show a b c d e f g aa bb cc dd ee ff gg AA BB CC DD a b c d e g f 0 0 1 0 1 1 0 1 1 1 0
- 14. BCD-to-7- Segment Decoder BCD-to-7-Segment Decoder • Decode“4” and show a b c d e f g aa bb cc dd ee ff gg AA BB CC DD a b c d e g f 0 1 0 0 0 1 1 0 0 1 1
- 15. BCD-to-7-Seg. Decoder TruthTable A B C D a b c d e f g 0 0 0 0 0 1 1 1 1 1 1 0 1 0 0 0 1 0 1 1 0 0 0 0 2 0 0 1 0 1 1 0 1 1 0 1 3 0 0 1 1 1 1 1 1 0 0 1 4 0 1 0 0 0 1 1 0 0 1 1 5 0 1 0 1 1 0 1 1 0 1 1 6 0 1 1 0 0 0 1 1 1 1 1 7 0 1 1 1 1 1 1 0 0 0 0 8 1 0 0 0 1 1 1 1 1 1 1 9 1 0 0 1 1 1 1 0 0 1 1 >10 All other inputs 0 0 0 0 0 0 0
- 16. Design Each OutputIndividually “a” A B C D a 0 0 0 0 0 1 1 0 0 0 1 0 2 0 0 1 0 1 3 0 0 1 1 1 4 0 1 0 0 0 5 0 1 0 1 1 6 0 1 1 0 0 7 0 1 1 1 1 8 1 0 0 0 1 9 1 0 0 1 1 >10 All other inputs 0 00 01 11 10 00 1 0 1 1 01 0 1 1 0 11 0 0 0 0 10 1 1 0 0 AB CD CBABDACDADBAa +++=
- 17. Design Each OutputIndividually “b” A B C D b 0 0 0 0 0 1 1 0 0 0 1 1 2 0 0 1 0 1 3 0 0 1 1 1 4 0 1 0 0 1 5 0 1 0 1 0 6 0 1 1 0 0 7 0 1 1 1 1 8 1 0 0 0 1 9 1 0 0 1 1 >10 All other inputs 0 00 01 11 10 00 1 1 1 1 01 1 0 1 0 11 0 0 0 0 10 1 1 0 0 AB CD CDADCABACBb +++=
- 18.
- 19. 4-to-2 Encoder D3 D2D1 D0 A1 A0 0 0 0 1 0 0 0 0 1 0 0 1 0 1 0 0 1 0 1 0 0 0 1 1 Since Dx=1 only in one column at a time A0 = D1 + D3 A1 = D2 + D3 00 01 11 10 00 X 0 X 1 01 0 X X X 11 X X X X 10 1 X X X D3 D2 D1 D0 D0D2orD3D1A0 += For A0 00 01 11 10 00 X 0 X 0 01 1 X X X 11 X X X X 10 1 X X X D3 D2 D1 D0 D0D1orD3D2A1 += For A1
- 20. 8-to-3 Encoder D7 D6D5 D4 D3 D2 D1 D0 A2 A1 A0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 1 1 1 Since Dx=1 only in one column at a time A0 = D1 + D3 + D5 + D7 A1 = D2 + D3 + D6 + D7 A2 = D4 + D5 + D6 + D7
- 21. Example 1 ofan Encoder Only point to one single reading at a time.
- 22. Example 2 ofan Encoder D0 D1 D2 D3 8-to-38-to-3 -line-line EncoderEncoder A0 A1 A2D4 D5 D6 D7 Amy Brian Cathy Dave Ellen Frank Gina Hugh Ac 0 0 0 0 Active or not 1 1 0 1 ? ? ? 1
- 23. 8-to-3 Priority Encoder D7D6 D5 D4 D3 D2 D1 D0 A2 A1 A0 Active 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 XX 0 0 1 1 0 0 0 0 0 1 XX XX 0 1 0 1 0 0 0 0 1 XX XX XX 0 1 1 1 0 0 0 1 XX XX XX XX 1 0 0 1 0 0 1 XX XX XX XX XX 1 0 1 1 0 1 XX XX XX XX XX XX 1 1 0 1 1 XX XX XX XX XX XX XX 1 1 1 1
- 24. 4-to-2 Priority Encoder D3D2 D1 D0 A1 A0 Active 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 XX 0 1 1 0 1 XX XX 1 0 1 1 XX XX XX 1 1 1 00 01 11 10 00 0 0 0 0 01 1 1 1 1 11 1 1 1 1 10 1 1 1 1 D3 D2 D1 D0 D3D2A1 += For A1 Or using simplification property D2D3D2D3D3A1 +=+=
- 25. 4-to-2 Priority Encoder D3D2 D1 D0 A1 A0 Active 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 XX 0 1 1 0 1 XX XX 1 0 1 1 XX XX XX 1 1 1 00 01 11 10 00 0 0 1 1 01 0 0 0 0 11 1 1 1 1 10 1 1 1 1 D3 D2 D1 D0 D1D2D3A0 += For A0 Or using simplification property D1D2D3D1D2D3D3A0 +=+=
- 26. 4-to-2 Priority Encoder D3D2 D1 D0 A1 A0 Active 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 XX 0 1 1 0 1 XX XX 1 0 1 1 XX XX XX 1 1 1 00 01 11 10 00 0 1 1 1 01 1 1 1 1 11 1 1 1 1 10 1 1 1 1 D3 D2 D1 D0 D0D1D2D3Active +++= For Active
- 27. 4-to-2 Priority EncoderSchematic D3D2A1 += D1D2D3A0 += D0D1D2D3Active +++= D3 D2 D1 D0 A1 A0 Active
- 28. 8-to-3 Priority Encoder(A2) D7 D6 D5 D4 D3 D2 D1 D0 A2 A1 A0 Active 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 XX 0 0 1 1 0 0 0 0 0 1 XX XX 0 1 0 1 0 0 0 0 1 XX XX XX 0 1 1 1 0 0 0 1 XX XX XX XX 1 0 0 1 0 0 1 XX XX XX XX XX 1 0 1 1 0 1 XX XX XX XX XX XX 1 1 0 1 1 XX XX XX XX XX XX XX 1 1 1 1 D7D6D5D4 D7D6D5D4D5 D7D6D5D6D4D5D6 D7D6D7D5D6D7D4D5D6D7A2 +++= +++= +++= +++=
- 29. 8-to-3 Priority Encoder(A1) D7 D6 D5 D4 D3 D2 D1 D0 A2 A1 A0 Active 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 XX 0 0 1 1 0 0 0 0 0 1 XX XX 0 1 0 1 0 0 0 0 1 XX XX XX 0 1 1 1 0 0 0 1 XX XX XX XX 1 0 0 1 0 0 1 XX XX XX XX XX 1 0 1 1 0 1 XX XX XX XX XX XX 1 1 0 1 1 XX XX XX XX XX XX XX 1 1 1 1 D7D6D3D4D5D2D4D5 D7D6D3)D2D3(D4D5 D7D6D3D4D5D2D3D4D5 D7D6D3D4D5D6D2D3D4D5D6 D7D6D7D3D4D5D6D7D2D3D4D5D6D7A1 +++= +++= +++= +++= +++=
- 30. 8-to-3 Priority Encoder(A0) D7 D6 D5 D4 D3 D2 D1 D0 A2 A1 A0 Active 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 XX 0 0 1 1 0 0 0 0 0 1 XX XX 0 1 0 1 0 0 0 0 1 XX XX XX 0 1 1 1 0 0 0 1 XX XX XX XX 1 0 0 1 0 0 1 XX XX XX XX XX 1 0 1 1 0 1 XX XX XX XX XX XX 1 1 0 1 1 XX XX XX XX XX XX XX 1 1 1 1 D7D5D6D3D4D6D1D2D4D6 D7D5)D3)D1D2(D4(D6D7D5)D3)D1D2D3(D4(D6 D7D5)D3D4D1D2D3D4(D6D7D5)D3D4D5D1D2D3D4D5(D6 D7D5D6D3D4D5D6D1D2D3D4D5D6 D7D5D6D7D3D4D5D6D7D1D2D3D4D5D6D7A0 +++= +++=+++= +++=+++= +++= +++=
- 31. 8-to-3 Priority Encoder(All) D7 D6 D5 D4 D3 D2 D1 D0 A2 A1 A0 Active 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 XX 0 0 1 1 0 0 0 0 0 1 XX XX 0 1 0 1 0 0 0 0 1 XX XX XX 0 1 1 1 0 0 0 1 XX XX XX XX 1 0 0 1 0 0 1 XX XX XX XX XX 1 0 1 1 0 1 XX XX XX XX XX XX 1 1 0 1 1 XX XX XX XX XX XX XX 1 1 1 1 D7D6D5D4D3D2D1Active D7D5D6D3D4D6D1D2D4D6A0 D7D6D3D4D5D2D4D5A1 D7D6D5D4A2 ++++++= +++= +++= +++=
- 32. 1-bit Magnitude Comparator AB A?B 0 0 A=B 0 1 A<B 1 0 A>B 1 1 A=B A B A > B A = B A < B BABA BABA BABA ⊕→= →< →> Single bit comparison
- 33. 2-bit Magnitude Comparator(unsigned) )BA)(BA(B)(A BA)BA(BAB)(A B)ABA(BAB)(A 0011 001111 001111 ⊕⊕→= ⊕+→< ⊕+→> A B A > B A = B A < B Two-bit comparison 2 2 A1A0 B1B0
- 34. 2-bit Magnitude Comparator(unsigned) A B A > B A = B A < B Two-bit comparison 2 2 A1A0 B1B0 01 00111 00111 nnn XXB)(A BAXBAB)(A BAXBAB)(A BAXAssign →= +→< +→> ⊕=
- 35. 3-bit Magnitude Comparator(unsigned) Three-bit comparison A2A1A0 B2B1B0 012 001211222 001211222 nnn XXXB)(A BAXXBAXBAB)(A BAXXBAXBAB)(A BAXAssign →= ++→< ++→> ⊕= A B A > B A = B A < B 3 3
- 36. 4-bit Magnitude Comparator(unsigned) 0123 00123112322333 00123112322333 nnn XXXXB)(A BAXXXBAXXBAXBAB)(A BAXXXBAXXBAXBAB)(A BAXAssign →= +++→< +++→> ⊕= Four-bit comparison A3A2A1A0 B3B2B1B0 A B A > B A = B A < B 4 4
- 37. 4-bit Magnitude Comparator 0123 00123112322333 00123112322333 nnn XXXXB)(A BAXXXBAXXBAXBAB)(A BAXXXBAXXBAXBAB)(A BAXAssign →= +++→< +++→> ⊕= B3A3 A2 A1A0B2 B1B0 X3 X2 X1 X0 A>B A<B A=B
- 38. Cascading Comparator A B A> B A = B A < B 4 4 AGTBin AGTBout AEQBout ALTBout Inputs from Prior stage (Lower order bitsLower order bits) AEQBin ALTBin Extra Comb. Logic Outputs to Next stage (Higher order bitsHigher order bits) AGTBoutAGTBout == (A>B) + (A=B) · AGTBin(A>B) + (A=B) · AGTBin AEQBoutAEQBout == (A=B) · AEQBin(A=B) · AEQBin ALTBoutALTBout == (A<B) + (A=B) · ALTBin(A<B) + (A=B) · ALTBin
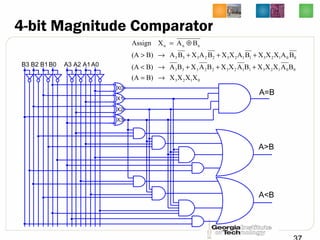
- 39. 16-bit Cascading Comparator AB AGTBin AEQBin ALTBin 4 4 AGTBout AEQBout ALTBout A[3:0] B[3:0] A B AGTBin AEQBin ALTBin 4 4 AGTBout AEQBout ALTBout A[7:4] B[7:4] A B AGTBin AEQBin ALTBin 4 4 AGTBout AEQBout ALTBout A[11:8] B[11:8] A B AGTBin AEQBin ALTBin 4 4 AGTBout AEQBout ALTBout A[15:12] B[15:12] 0 1 0 A>B A<B A=B B[15:0] A[15:0]