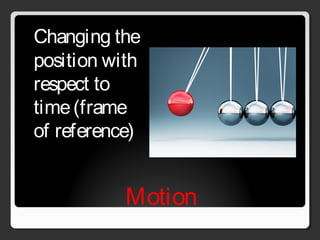
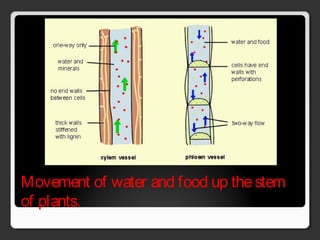
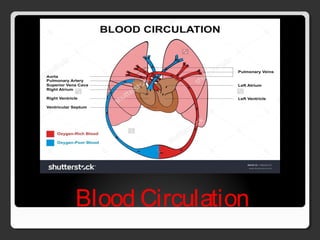
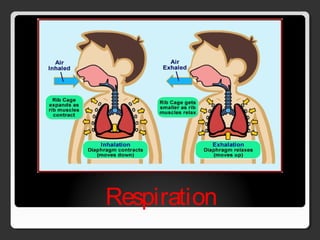
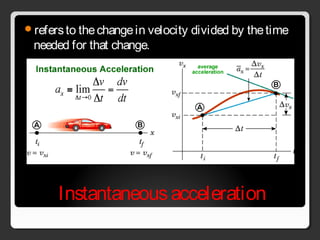
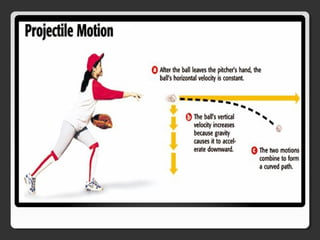
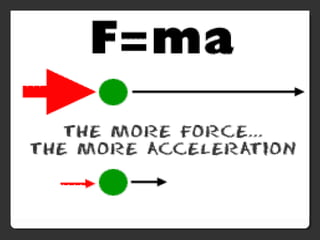
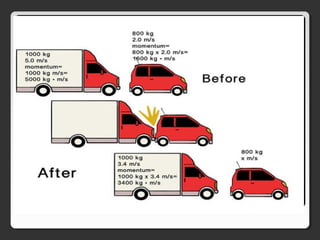
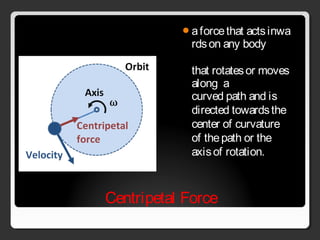
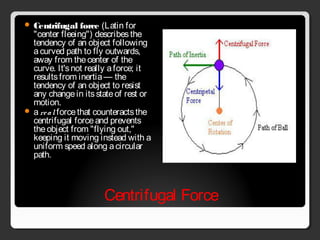
The document covers various concepts in motion, including speed, velocity, acceleration, and specific examples of problems related to these topics, such as calculations involving cars and free-falling bodies. It also delves into projectile motion, the law of universal gravitation, impulse, momentum, and conservation of momentum with corresponding practice problems. Additionally, it explains uniform circular motion and the related forces, including centripetal and centrifugal forces.

1. Motion
By Prof. Liwayway Memije-Cruz

2. Motion
Changing the
position with
respect to
time(frame
of reference)

3. RelativeMotion

4. Examplesof Motion

5. Movement of water and food up thestem
of plants.

6. Blood Circulation

7. Respiration

8. Speed
 ratio of a
distancecovered
by abody to the
time
 speed =
distance/time
 scalar

9. Averagevelocity
rateof displacement
Displacement – changein theposition of the
body specified by length and adirection per
unit of time
Vector (rateand direction)
Speed with direction

10. Instantaneousvelocity
 indicateshow fast an object movesat
itsinstant of timeand direction of that
motion

11. Averageacceleration
Acceleration – rateof increaseor gain in the
speed or velocity of abody
Deceleration – negativeacceleration

12. Instantaneousacceleration
refersto thechangein velocity divided by thetime
needed for that change.

13. Uniformly accelerated motion
Refersto themotion in straight linein which
thedirection isalwaysthesameand the
speed changesat aconstant rate.

15. Problem 1: From rest, acar accelerated at 8
m/s2
for 10 seconds.
a) What istheposition of thecar at theend of
the10 seconds?
b) What isthevelocity of thecar at theend of
the10 seconds?

16. Solution to Problem 1:
a) Thecar startsfrom rest thereforetheinitial speed u = 0. Nothing issaid
about theinitial position and wethereforeassumeit isequal to 0. Hence
theposition x isgiven by theequation
x = (1/2) at 2
whereaistheacceleration (=8 m/s2
) and t istheperiod of timebetween
initial and final positions
x = (1/2)8 (10)2
= 400 m
b) Thevelocity v of thecar at theend of the10 secondsisgiven by
v = at = 8 * 10 = 80 m/s

17. Problem 2: With an initial velocity of 20
km/h, acar accelerated at 8 m/s2
for 10
seconds.
a) What istheposition of thecar at the
end of the10 seconds?
b) What isthevelocity of thecar at the
end of the10 seconds?

18. Solution to Problem 2:
a) Thecar hasan initial velocity of 20 km/h, thereforetheinitial speed u =
20 km/h. Nothing issaid about theinitial position and wetherefore
assumeit isequal to 0. Hencetheposition x isgiven by theequation
x = (1/2) at2
+ u t
whereaistheacceleration (=8 m/s2
) and t isperiod of timebetween initial
and final positionsand u istheinitial velocity.
Sincethetimeisgiven in seconds, weneed to convert 20 km/h into m/sas
follows:
u = 20 km/h = 20 * 1km/1 hour x 1000m/1kmx 1hour/3600 sec = 5.6 m/s
Wenow have
x = (1/2) (8) 102
+ 5.6*10 = 456 m
b) v = at + u = 8*10 + 5.6 = 85.6 m/s

19. Problem 3: A car acceleratesuniformly from
0 to 72 km/h in 11.5 seconds.
a) What istheacceleration of thecar in m/s2
?
b) What istheposition of thecar by thetime
it reachesthevelocity of 72 km/h?

20. Freely Falling body: (dueto gravity)

22. A stoneisdropped into adeep well and isheard to hit the
water 3.41 safter being dropped. Determinethedepth of the
well.
Given:
a= -9.8 m/s2
t = 3.41 s
vi = 0 m/s
Find:
d = ??d = vi*t + 0.5*a*t2
d = (0 m/s)*(3.41 s)+ 0.5*(-9.8 m/s2
)*(3.41 s)2
d = 0 m+ 0.5*(-9.8 m/s2
)*(11.63 s2
)
d = -57.0 m

23. Problem No. 4
Theobservation deck of tall
skyscraper 370 m abovethestreet.
Determinethetimerequired for a
penny to freefall from thedeck to
thestreet below.

24. Given:
vi = 0 m/s
d = -370 m
a= -9.8 m/s2
Find:
t = ??d = vi*t + 0.5*a*t2
-370 m = (0 m/s)*(t)+ 0.5*(-9.8 m/s2
)*(t)2
-370 m = 0+ (-4.9 m/s2
)*(t)2
(-370 m)/(-4.9 m/s2
) = t2
75.5 s2
= t2
t = 8.69 s

26. ProjectileMotion
A projectileisan object upon which theonly forceis
gravity. Gravity actsto influencethevertical motion of
theprojectile, thuscausing avertical acceleration. The
horizontal motion of theprojectileistheresult of the
tendency of any object in motion to remain in motion at
constant velocity. Dueto theabsenceof horizontal
forces, aprojectileremainsin motion with aconstant
horizontal velocity. Horizontal forcesarenot required to
keep aprojectilemoving horizontally. Theonly force
acting upon aprojectileisgravity.

27. Defining Projectiles
A projectileisan object upon which theonly forceacting
isgravity. Thereareavariety of examplesof projectiles.
An object dropped from rest isaprojectile(pro vided that
the influence o f air resistance is negligible ). An object
that isthrown vertically upward isalso aprojectile
(pro vided that the influence o f air resistance is
negligible). And an object which isthrown upward at an
angleto thehorizontal isalso aprojectile(pro vided that
the influence o f air resistance is negligible). A projectile
isany object that oncepro jected or dropped continuesin
motion by itsown inertiaand isinfluenced only by the
downward forceof gravity.

34. Law of Universal Gravitation

35. Impulseand Momentum
 When atennisracquet hitsa
tennisball, theforceof the
racquet on theball deliversan
impulseto theball whilethe
ball isin contact with the
racquet. Themagnitudeof the
forceof theracquet on theball
varieswith time, starting low at
initial contact, then reaching a
maximum when theball
compression and racquet string
deformity reachesamaximum,
beforereducing back to zero as
theball leavestheracquet
strings.

36. Conservation of Momentum
Law of Conservation of Momentum statesthat when any two
bodiesact upon another body, their total momentum remains
constant provided no external forcesareacting. That means
whenever onebody gainsmomentum, then someother body
losean equal amount of momentum, that is, momentum is
never destroyed nor created. Therefore, law of conservation
of momentum isalso known asprincipleof conservation of
momentum.

38. Conservation of Momentum PracticeProblems
1.Two grocery cartscollide, afull onewith amassof 35 kg
moving East at 2 m/sand an empty onewith amassof 10 kg
moving West at 3 m/s. After thecollision thefull cart is
moving East at 0.75m/s. What isthevelocity of theempty
cart?
2. Two football playershaveahead on collision and grab onto
each other’suniforms. The80 kg PennridgeRam wasmoving
at 3 m/s, whilethe70 kg Souderton player wasmoving in the
oppositedirection at 2.5 m/s. What istheir final velocity
impact?

39.  Two carshavea‘rear end’ collision. A
1200 kg Hondamoving at 20 m/sstrikesa
1000 kg Ford moving at 15 m/s. Their
bumpersbecomelocked and they continue
to moveasonemass. What istheir final
velocity?

40.  Answers
1.1.375 m/s
2.0.433 m/s
3.17.73 m/s

41. Coefficient of Restitution
For acollision between two
objects, thecoefficient of
restitution istheratio of the
relativespeed after to the
relativespeed beforethe
collision.
Thecoefficient of restitution
isanumber between 0
(perfectly inelastic collision)
and 1 (elastic collision)
inclusive.

42. Uniform Circular Motion
themotion of an object in a
circleat aconstant speed.
Asan object movesin a
circle, it isconstantly
changing itsdirection. At
all instances, theobject is
moving tangent to the
circle. Sincethedirection
of thevelocity vector isthe
sameasthedirection of the
object'smotion, the
velocity vector isdirected
tangent to thecircleaswell

43. Uniform Circular Motion

44. Centripetal Force
a force that acts inwa
rds on any body
that rotates or moves
along a
curved path and is
directed towards the
center of curvature
of the path or the
axis of rotation.

45. Centrifugal Force
 Centrifugal force (Latin for
"center fleeing") describesthe
tendency of an object following
acurved path to fly outwards,
away from thecenter of the
curve. It'snot really aforce; it
resultsfrom inertia— the
tendency of an object to resist
any changein itsstateof rest or
motion.
 a real forcethat counteractsthe
centrifugal forceand prevents
theobject from "flying out,"
keeping it moving instead with a
uniform speed along acircular
path.