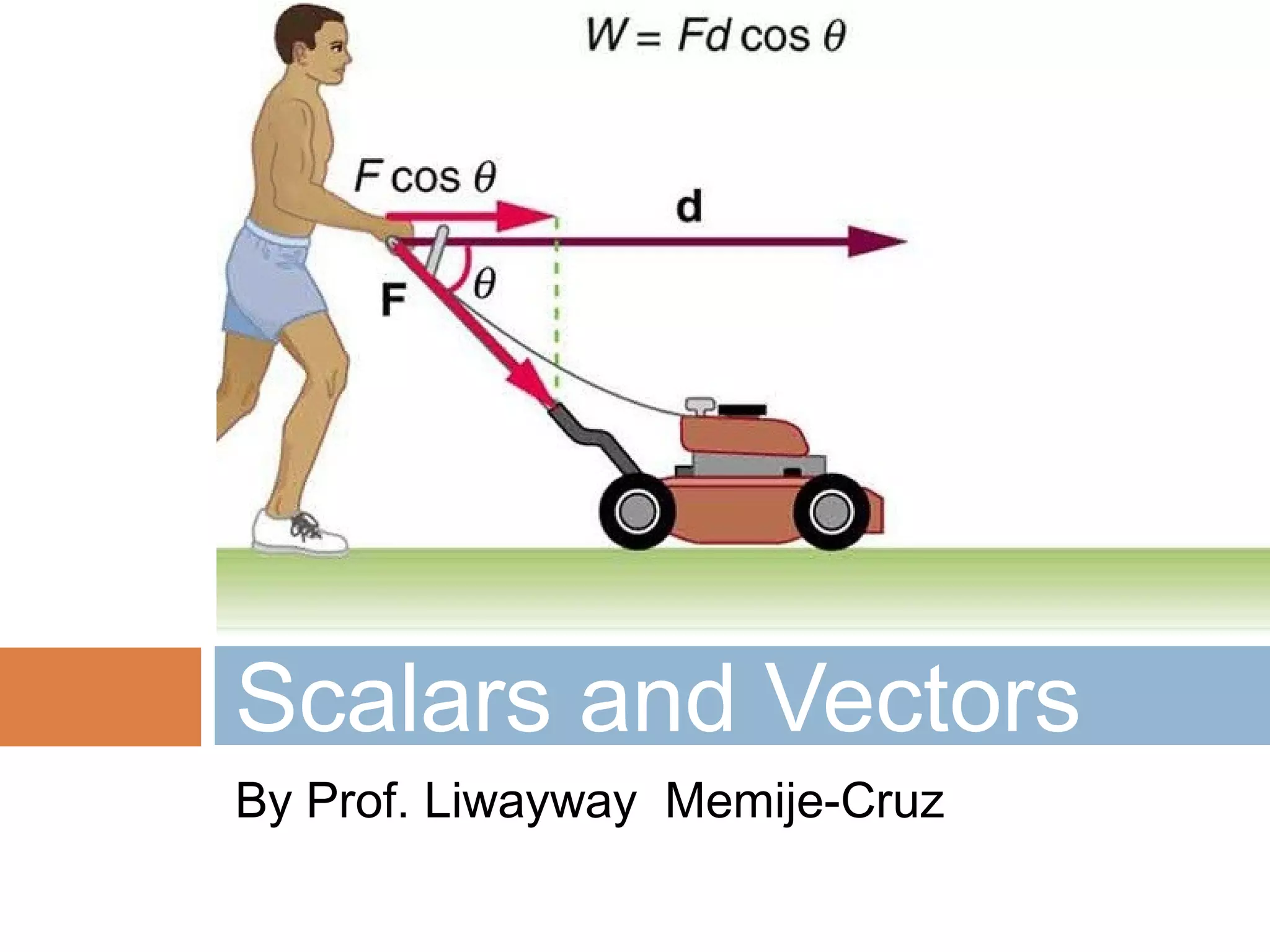
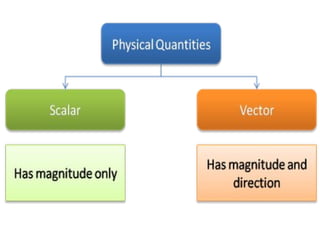
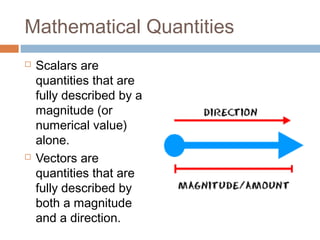
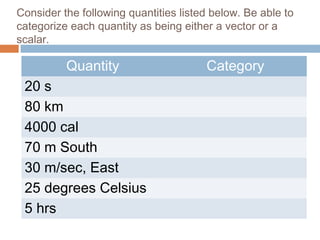
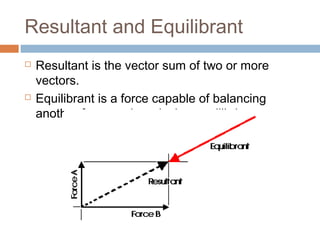
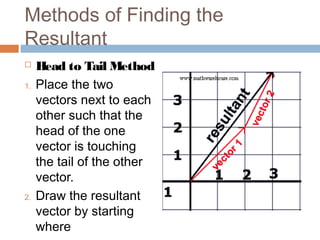
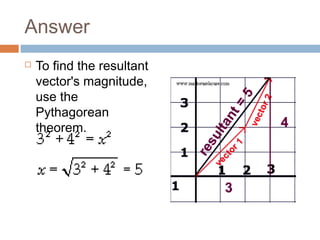
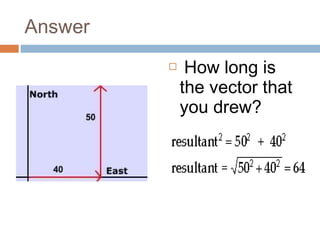
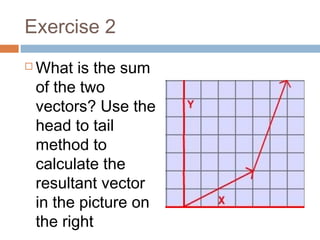
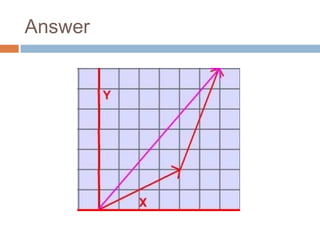
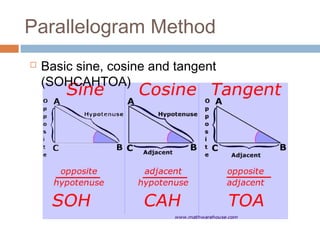
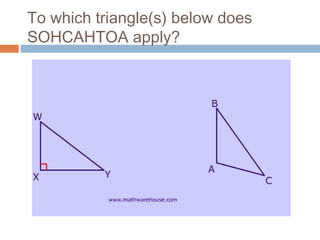
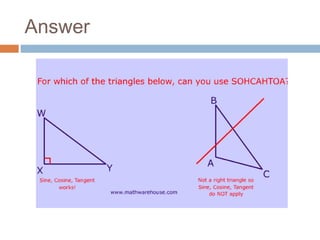
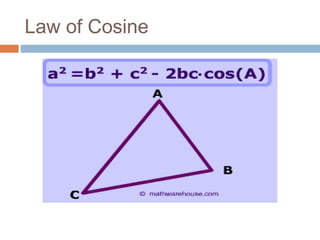
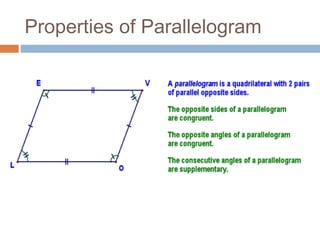
The document provides an introduction to scalars and vectors in physics, highlighting the mathematical basis for concepts like distance, speed, and acceleration. It distinguishes between scalars, which have only magnitude, and vectors, which have both magnitude and direction, and illustrates methods to find resultant vectors using head-to-tail and parallelogram methods. Additionally, it includes exercises to apply these concepts, such as calculating resultant vectors and utilizing the law of sines and cosines.

1. By Prof. Liwayway Memije-Cruz
Scalars and Vectors

2. Introduction
 Physics is a mathematical science.
 Its concepts and principles have a
mathematical basis.
 Mo tio n o f o bje cts in physics are e xpre sse d by
distance , displace m e nt, spe e d, ve lo city, and
acce le ratio n which are asso ciate d with
mathematical quantities.
 Mathematical quantities used to describe the
motion of objects are vector and a scalar.

4. Mathematical Quantities
 Scalars are
quantities that are
fully described by a
magnitude (or
numerical value)
alone.
 Vectors are
quantities that are
fully described by
both a magnitude
and a direction.

5. Consider the following quantities listed below. Be able to
categorize each quantity as being either a vector or a
scalar.
Quantity Category
20 s
80 km
4000 cal
70 m South
30 m/sec, East
25 degrees Celsius
5 hrs

6. Resultant and Equilibrant
 Resultant is the vector sum of two or more
vectors.
 Equilibrant is a force capable of balancing
another force and producing equilibrium.

7. Methods of Finding the
Resultant
 Head to Tail Method
1. Place the two
vectors next to each
other such that the
head of the one
vector is touching
the tail of the other
vector.
2. Draw the resultant
vector by starting
where

8. Answer
 To find the resultant
vector's magnitude,
use the
Pythagorean
theorem.

9. Exercise 1
1. You left your house to visit your
sister. You got in your car drove 40
miles east, then got on a highway
and went 50 miles north.
2. Draw a vector from the beginning
of your journey, your home, and the
end, your friend’s house.

10. Answer
 How long is
the vector that
you drew?

11. Exercise 2
 What is the sum
of the two
vectors? Use the
head to tail
method to
calculate the
resultant vector
in the picture on
the right

12. Answer

13. Parallelogram Method
 Basic sine, cosine and tangent
(SOHCAHTOA)

14. To which triangle(s) below does
SOHCAHTOA apply?

15. Answer

16. Law of Cosine

17. Law of Sines
 The law of sines
provides a formula
that relates the
sides with the
angles of a triangle.
This formula allows
you to relatively
easily find the side
length or the angle
of any triangle.

18. Properties of Parallelogram

19. Exercise 3
 To best understand how the parallelogram method
works, examine the two vectors below. The vectors have
magnitudes of 17 and 28 and the angle between them is
66°. Use the parallelogram method to determine the
magnitude of the resultant.

20.  Step 1) Draw a parallelogram based on the
two vectors that you already have. These
vectors will be two sides of the parallelogram
(not the opposite sides since they have the
angle between them)
 Step 2) We now have a parallelogram and
know two angles (opposite angles of
parallelograms are congruent). We can also
figure out the other pair of angles since the
other pair are congruent and all four angles
must add up to 360.

21. Step 3 Draw the
parallelograms diagonal. This
diagonal is the resultant
vector.
Step 4 Use the law of cosines
to determine the length of the
resultant

22.  Use the law of cosines to
calculate the resultant.

23. References:
 http://www.mathwarehouse.com/vectors/result
ant-vector.php#headToTailMethod
 http://www.s-cool.co.uk/a-
level/physics/vectors-and-scalars-and-linear-
motion/revise-it/resolving
 http://www.physicsclassroom.com/class/vector
s/Lesson-1/Vector-Addition
 http://www.physicsclassroom.com/class/vector
s/Lesson-1/Resultants