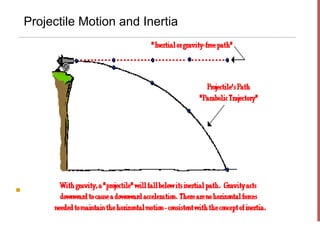
This document provides an overview of projectile motion concepts including: - A projectile is any object upon which the only force acting is gravity and it moves in a parabolic trajectory. - The horizontal motion of a projectile is independent of its vertical motion, with the horizontal velocity remaining constant and no horizontal acceleration. Vertically, gravity causes acceleration of -9.8 m/s2. 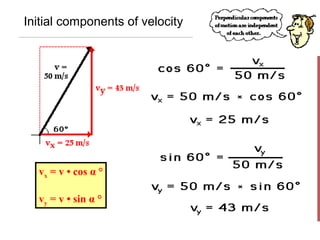- Key equations presented include those relating the horizontal and vertical displacement and velocity as functions of time, as well as resolving initial velocity into horizontal and vertical components using trigonometry. 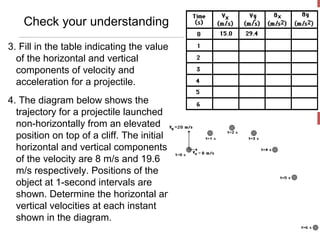- Examples are provided of solving projectile motion problems by identifying knowns and unknowns, selecting appropriate equations, and applying a

1. Projectile Motion or
2D Kinematics
By Sandrine Colson-Inam, Ph.D
References:
Conceptual Physics, Paul G. Hewitt, 10 th edition, Addison

Wesley publisher
 http://www.glenbrook.k12.il.us/gbssci/Phys/Class/vectors/u3l

2. Outline
 What is a projectile
 Characteristics of a projectile's motion
 Horizontal and vertical components of
velocity and displacement
 Initial velocity components
 Examples of problems

3. What is a projectile?
 A projectile is an object upon which the only force
acting is gravity. A projectile is any object which once
projected or dropped continues in motion by its own
inertia and is influenced only by the downward force of
gravity.

4. Projectile Motion and Inertia


5. Horizontal and Vertical Velocities

A projectile is any object upon which the only force is gravity,

Projectiles travel with a parabolic trajectory due to the influence of
gravity,

There are no horizontal forces acting upon projectiles and thus no
horizontal acceleration,

The horizontal velocity of a projectile is constant (a never changing
value),

There is a vertical acceleration caused by gravity; its value is 9.8
m/s/s, down,

The vertical velocity of a projectile changes by 9.8 m/s each
second,

The horizontal motion of a projectile is independent of its vertical
motion.

6. Vector diagrams for projectile motion
TIME HORIZONTAL VELOCITY VERTICAL VELOCITY
0s 73.1 m/s, right 19.6 m/s, up
1s 73.1 m/s, right 9.8 m/s, up
2s 73.1 m/s, right 0 m/s
3s 73.1 m/s, right 9.8 m/s, down
4s 73.1 m/s, right 19.6 m/s, down
5s 73.1 m/s, right 29.4 m/s, down
6s 73.1 m/s, right 39.2 m/s, down
7s 73.1 m/s, right 49.0 m/s, down

7. Horizontal and vertical displacement –
Horizontally Launched Projectile
If the horizontal displacement (x) of a projectile were
represented by an equation, then that equation would be
written as
x = vix • t
y = 0.5 • g • t2
(equation for vertical displacement for a horizontally
launched projectile)

8. Displacement diagram of projectile motion
Horizontal Vertical
TIME DISPLACEMENT DISPLACEMENT
0s 0m 0m
1s 20 m -4.9 m
2s 40 m -19.6 m
3s 60 m -44.1 m
4s 80 m -78.4 m
5s 100 m -122.5 m

9. Horizontal and vertical displacement : Non -
Horizontally Launched Projectile
y = viy • t + 0.5 • g • t2
(equation for vertical displacement for an
angled-launched projectile)
If the horizontal displacement (x) of a projectile were
represented by an equation, then that equation would be
written as
x = vix • t

10. Check your understanding
1. Anna Litical drops a ball from rest from
the top of 78.4-meter high cliff. How
much time will it take for the ball to
reach the ground and at what height will
the ball be after each second of motion?
2. A cannonball is launched horizontally
from the top of an 78.4-meter high cliff.
How much time will it take for the ball to
reach the ground and at what height will
the ball be after each second of travel?

11. Answers
1.
 It will take 4 seconds to fall 78.4 meters
 Use the equation y = 0.5 • g • t 2 and substitute -9.8 m/s/s for g. The vertical displacement must then be
subtracted from the initial height of 78. 4 m.
 At t = 1 s, y = 4.9 m (down) so height is 73.5 m (78.4 m - 4.9 m )
 At t = 2 s, y = 19.6 m (down) so height is 58.8 m (78.4 m - 19.6 m )
 At t = 3 s, y = 44.1 m (down) so height is 34.3 m (78.4 m - 45 m)
 At t = 4 s, y = 78.4 m (down) so height is 0 m (78.4 m - 78.4 m)
2.
 It will take 4 seconds to fall 78.4 meters
 Use the equation y = 0.5 • g • t 2 and substitute -9.8 m/s/s for g. The vertical displacement must then be
subtracted from the initial height of 78. 4 m.
 At t = 1 s, y = 4.9 m (down) so height is 73.5 m (78.4 m - 4.9 m )
 At t = 2 s, y = 19.6 m (down) so height is 58.8 m (78.4 m - 19.6 m )
 At t = 3 s, y = 44.1 m (down) so height is 34.3 m (78.4 m - 45 m)
 At t = 4 s, y = 78.4 m (down) so height is 0 m (78.4 m - 78.4 m)

12. Check your understanding
3. Fill in the table indicating the value
of the horizontal and vertical
components of velocity and
acceleration for a projectile.
4. The diagram below shows the
trajectory for a projectile launched
non-horizontally from an elevated
position on top of a cliff. The initial
horizontal and vertical components
of the velocity are 8 m/s and 19.6
m/s respectively. Positions of the
object at 1-second intervals are
shown. Determine the horizontal and
vertical velocities at each instant
shown in the diagram.

13. Answers
3.The v values will remain constant at 15.0 m/s for the entire 6 seconds; the a values will be 0 m/s/s for the
x x
entire 6 seconds.
 The vy values will be changing by -9.8 m/s each second. Thus,
 vy = 29.4 m/s (t = 0 s) vy = 19.6 m/s (t = 1 s)
 vy = 9.8 m/s (t = 2 s) vy = 0 m/s (t = 3 s)
 vy = -9.8 m/s (t = 4 s) vy = -19.6 m/s (t = 5 s)
 vy = -29.4 m/s (t = 6 s)
 The ay values will be -9.8 m/s/s for the entire 6 seconds.
4.The v values will remain 8 m/s for the entire 6 seconds.
x
 The vy values will be changing by 9.8 m/s each second. Thus,
 vy =9.8 m/s (t = 1 s) vy = 0 m/s (t = 2 s)
 vy = -9.8 m/s (t = 3 s) vy = -19.6 m/s (t = 4 s)
 vy = -29.4 m/s (t = 5 s) vy = -39.2 m/s (t = 6 s)

14. Initial components of velocity
vx = v • cos α °
vy = v • sin α °

15. Evaluating various info
 Determination of the Time of Flight
 Determination of Horizontal Displacement
x = vix • t
 Determination of the Peak Height
y = viy • t + 0.5 • g • t2

16. the vertical acceleration of a projectile is known to be -9.8 m/s/s
Equations of motion
 Horizontal motion
 Vertical Motion

17. Solving Projectile Motion Problems
 The following procedure summarizes the above problem-solving
approach.

Carefully read the problem and list known and unknown
information in terms of the symbols of the kinematic equations.
For convenience sake, make a table with horizontal information
on one side and vertical information on the other side.

Identify the unknown quantity which the problem requests you to
solve for.

Select either a horizontal or vertical equation to solve for the
time of flight of the projectile.

With the time determined, use one of the other equations to
solve for the unknown. (Usually, if a horizontal equation is used
to solve for time, then a vertical equation can be used to solve
for the final unknown quantity.)

18. Check your understanding
 A football is kicked with an initial velocity of 25 m/s at an angle of
45-degrees with the horizontal. Determine the time of flight, the
horizontal displacement, and the peak height of the football.

19. Horizontal Info Vertical Info
Answer x = ??? y = ???
vix = 17.7 m/s viy = 17.7 m/s
vfx = 17.7 m/s vfy = -17.7 m/s
 State the problem a x = 0 m/s/s a y = -9.8 m/s/s
 Use the appropriate equations of motion
 The unknown quantities are the horizontal displacement, the time of flight, and the height of the football at its peak.
 From the vertical information in the table above and the second equation listed among the vertical kinematic equations (vfy = viy + ay*t), it becomes obvious that the time of flight of the
projectile can be determined. By substitution of known values, the equation takes the form of -17.7 m/s = 17.7 m/s + (-9.8 m/s/s)•t
-35.4 m/s = (-9.8 m/s/s)•t
3.61 s = t
The total time of flight of the football is 3.61 seconds.
 With the time determined, information in the table and the horizontal kinematic equations can be used to determine the horizontal displacement (x) of the projectile. The first equation
(x = vix•t + 0.5•ax•t2) listed among the horizontal kinematic equations is suitable for determining x. With the equation selected, the physics problem once more becomes transformed
into an algebra problem. By substitution of known values, the equation takes the form of x = (17.7 m/s)•(3.6077 s) + 0.5•(0 m/s/s)•(3.6077 s)2
x = (17.7 m/s)•(3.6077 s)
x = 63.8 m
The horizontal displacement of the projectile is 63.8 m.
 Finally, the problem statement asks for the height of the projectile at is peak. This is the same as asking, "what is the vertical displacement (y) of the projectile when it is halfway
through its trajectory?" In other words, find y when t = 1.80 seconds (one-half of the total time). To determine the peak height of the projectile (y with t = 1.80 sec), the first equation (y
= viy•t +0.5•ay•t2) listed among the vertical kinematic equations can be used. By substitution of known values into this equation, it takes the form of
y = (17.7 m/s)•(1.80 s) + 0.5*(-10 m/s/s)•(1.80 s)2
y = 31.9 m + (-15.9 m)
y = 15.9 m
 The solution to the problem statement yields the following answers: the time of flight of the football is 3.61 s, the horizontal displacement of the football is 63.8 m, and the peak height
of the football 15.9 m.

20. The Problem-Solving Approach
The following procedure summarizes the above problem-solving approach.

Use the given values of the initial velocity (the magnitude and the angle) to determine
the horizontal and vertical components of the velocity (vix and viy).

Carefully read the problem and list known and unknown information in terms of the
symbols of the kinematic equations. For convenience sake, make a table with
horizontal information on one side and vertical information on the other side.

Identify the unknown quantity which the problem requests you to solve for.

Select either a horizontal or vertical equation to solve for the time of flight of the
projectile. For non-horizontally launched projectiles, the second equation listed among
the vertical equations (vfy = viy + ay*t) is usually the most useful equation.

With the time determined, use a horizontal equation (usually x = vix*t + 0.5*ax*t2 ) to
determine the horizontal displacement of the projectile.

Finally, the peak height of the projectile can be found using a time value which one-
half the total time of flight. The most useful equation for this is usually y = viy*t
+0.5*ay*t2 .

21. SUMMARY: See
Hand-outs