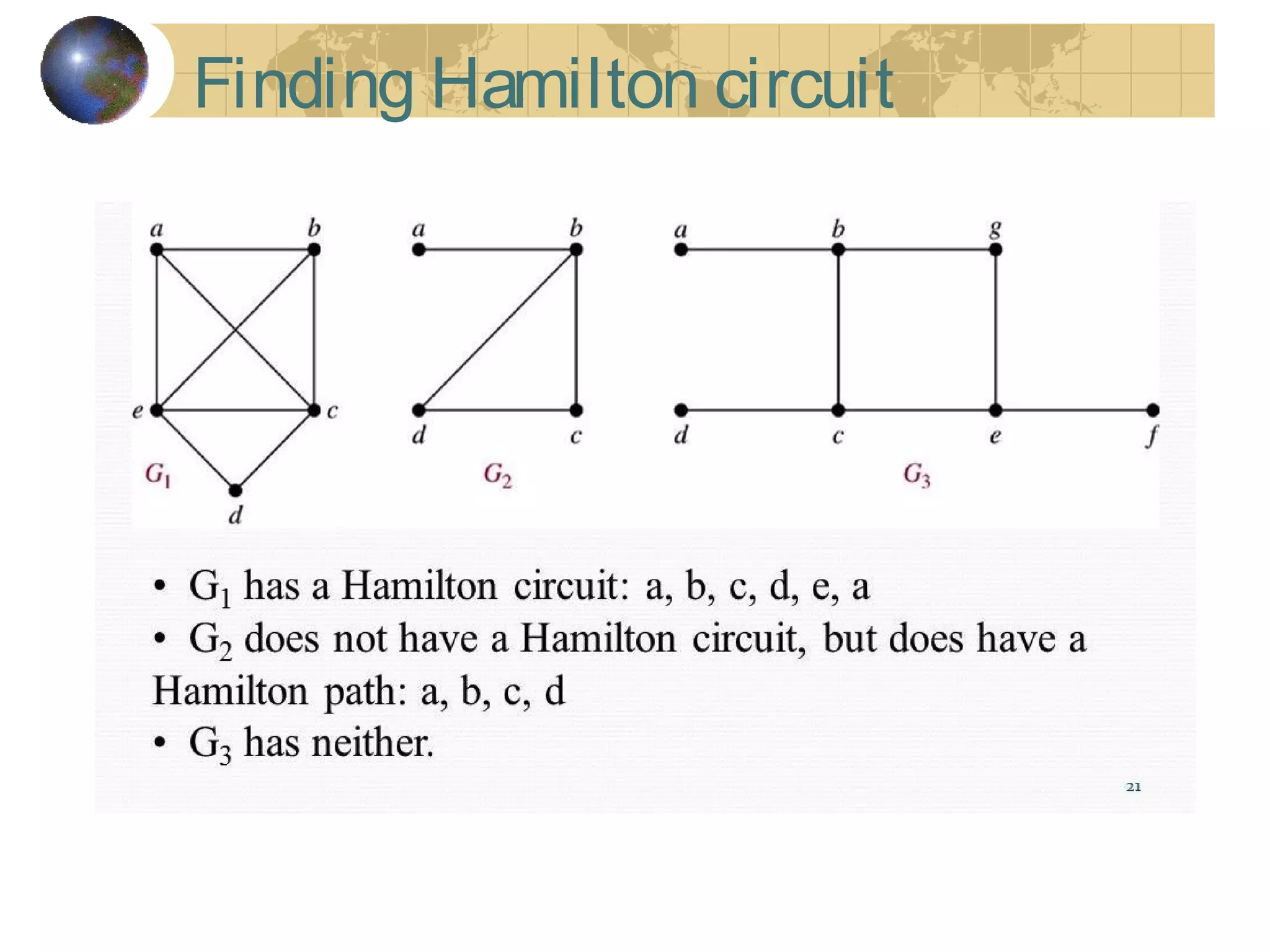
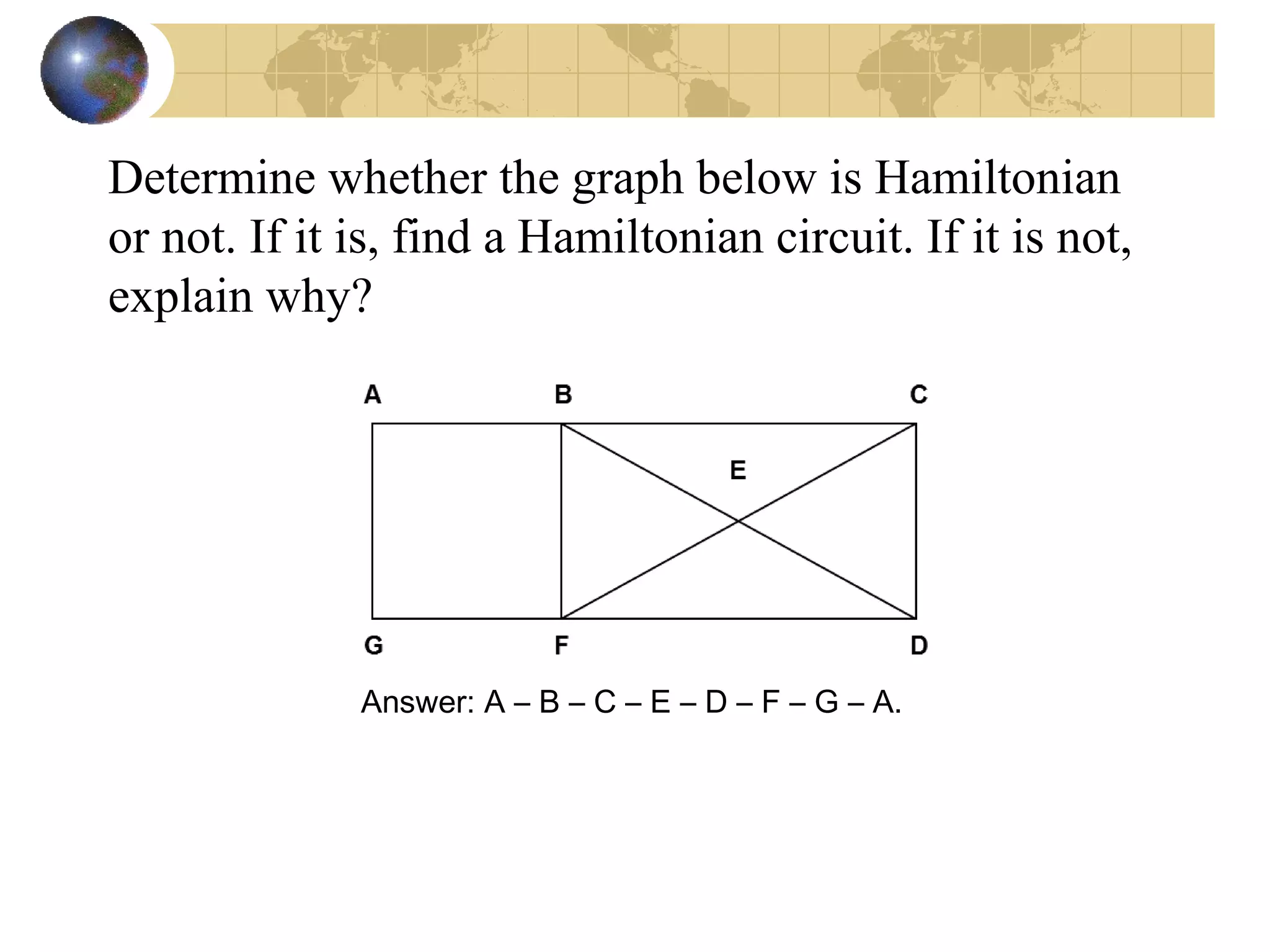
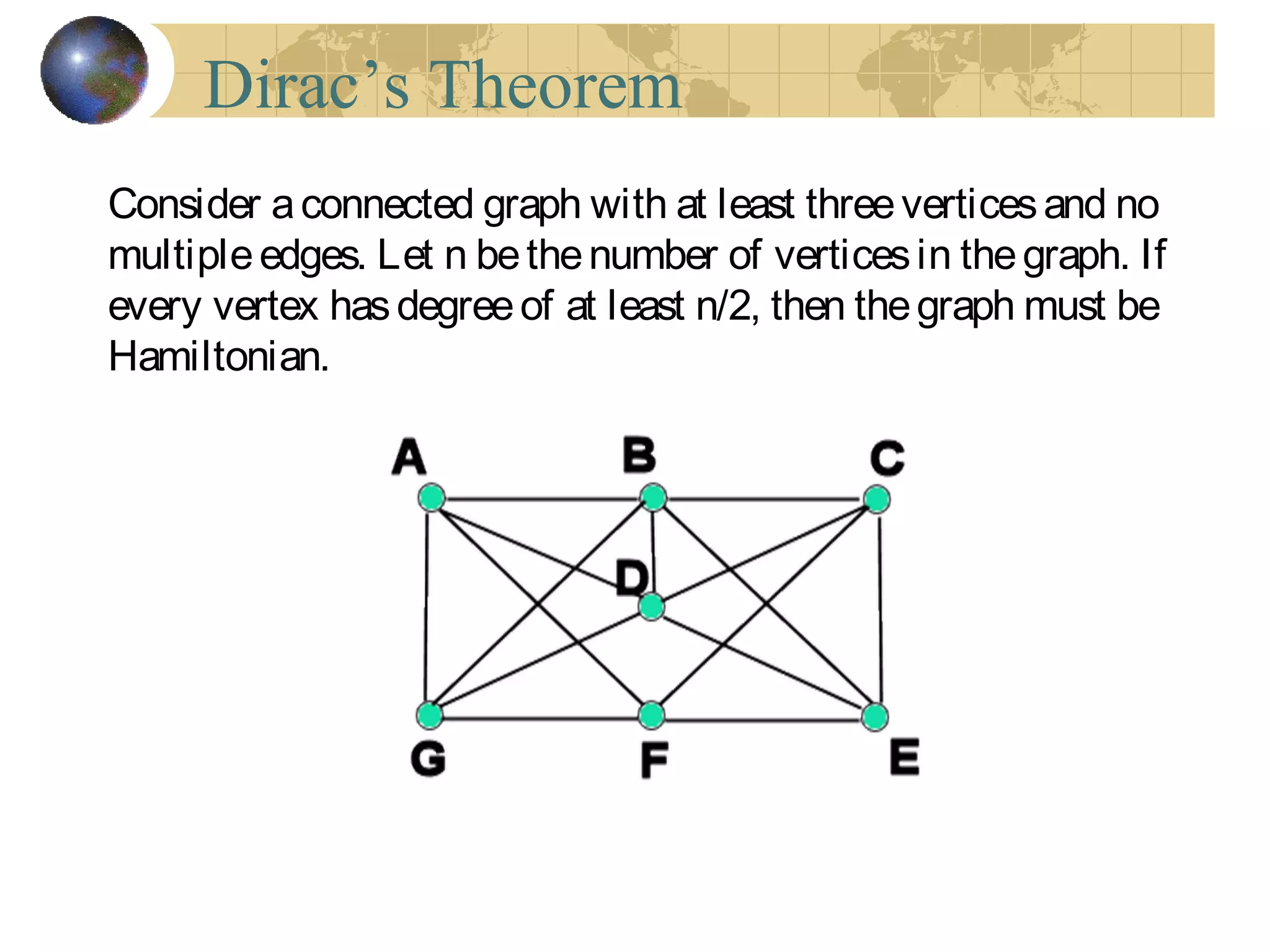
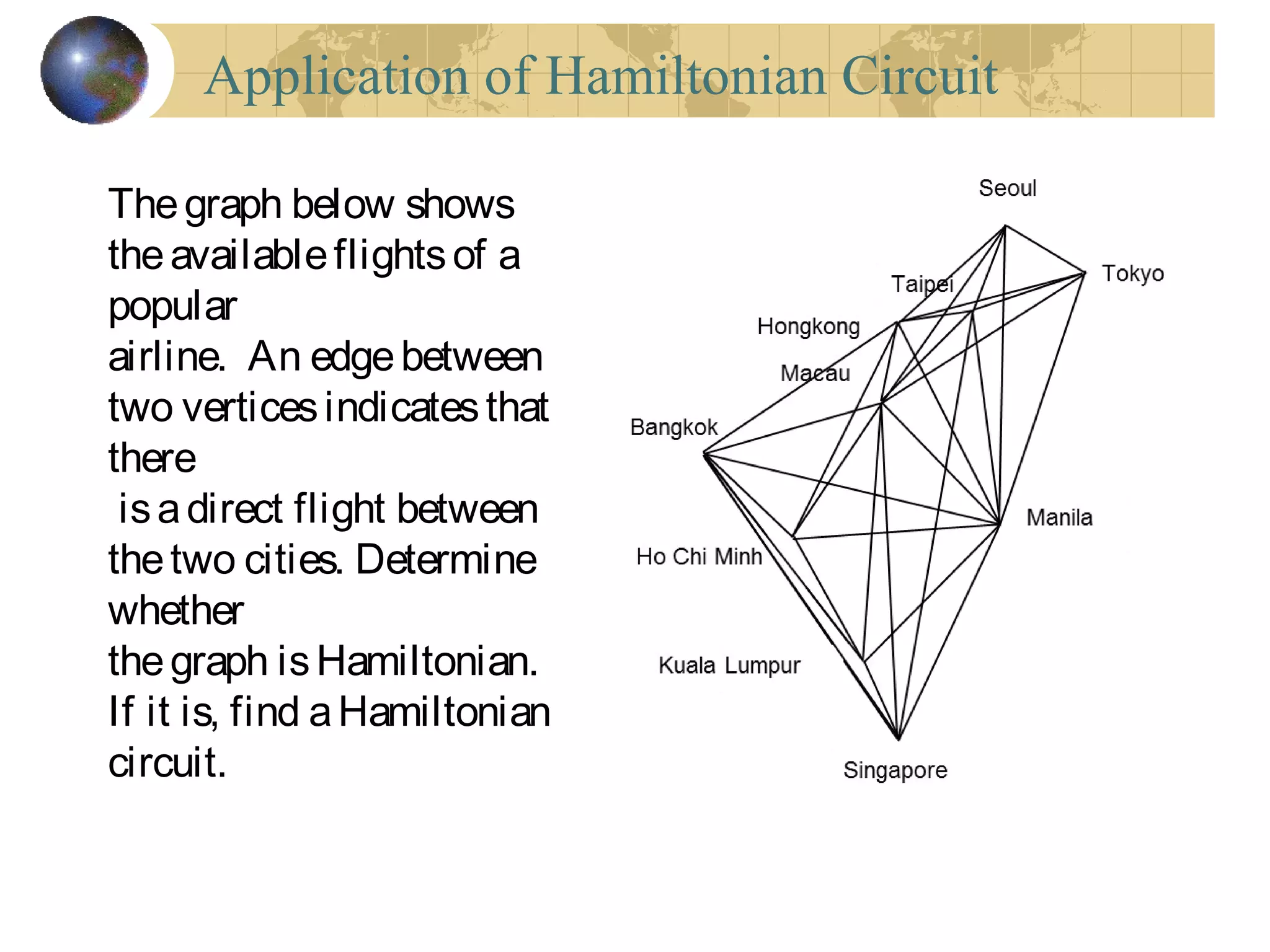
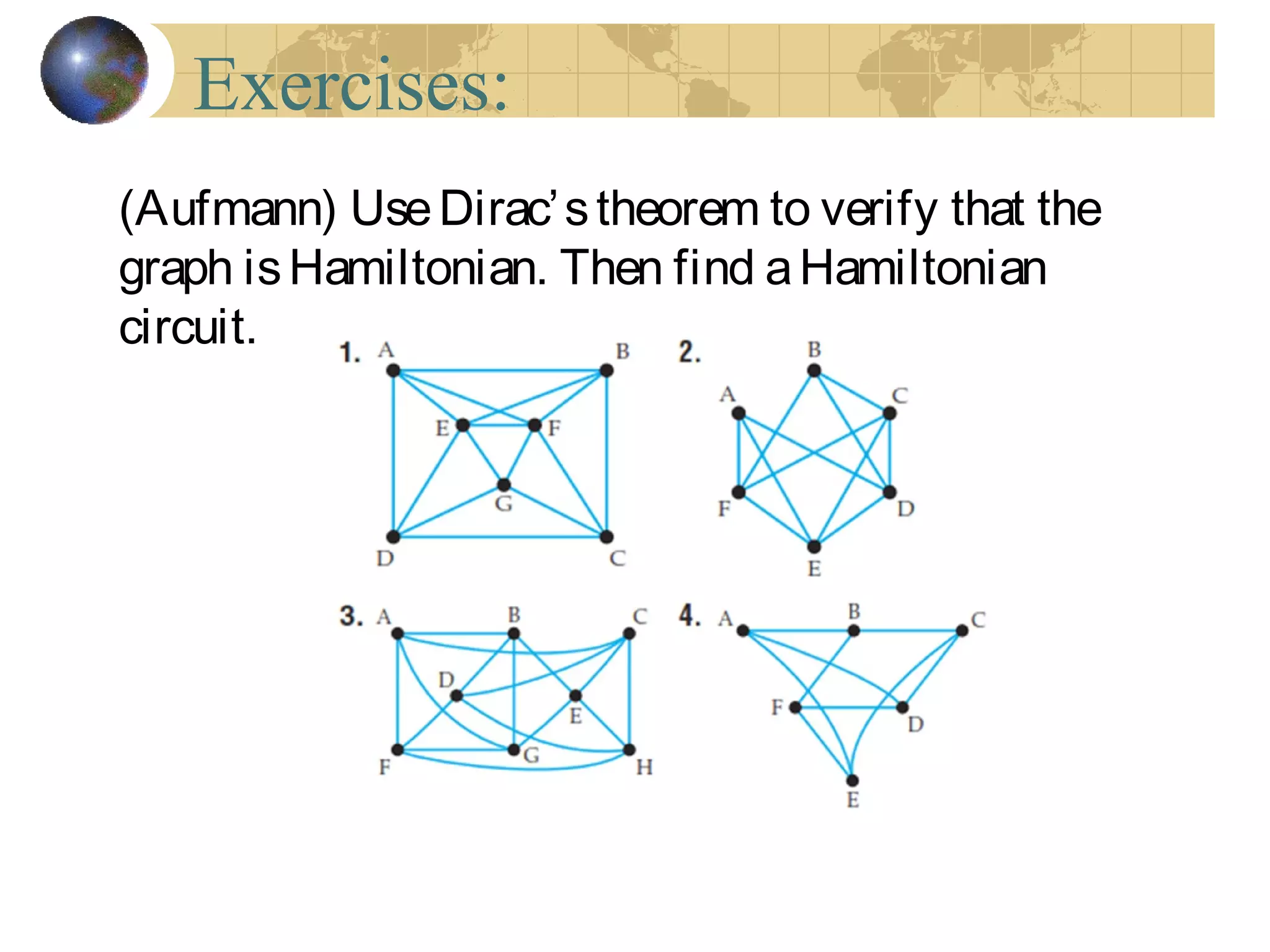
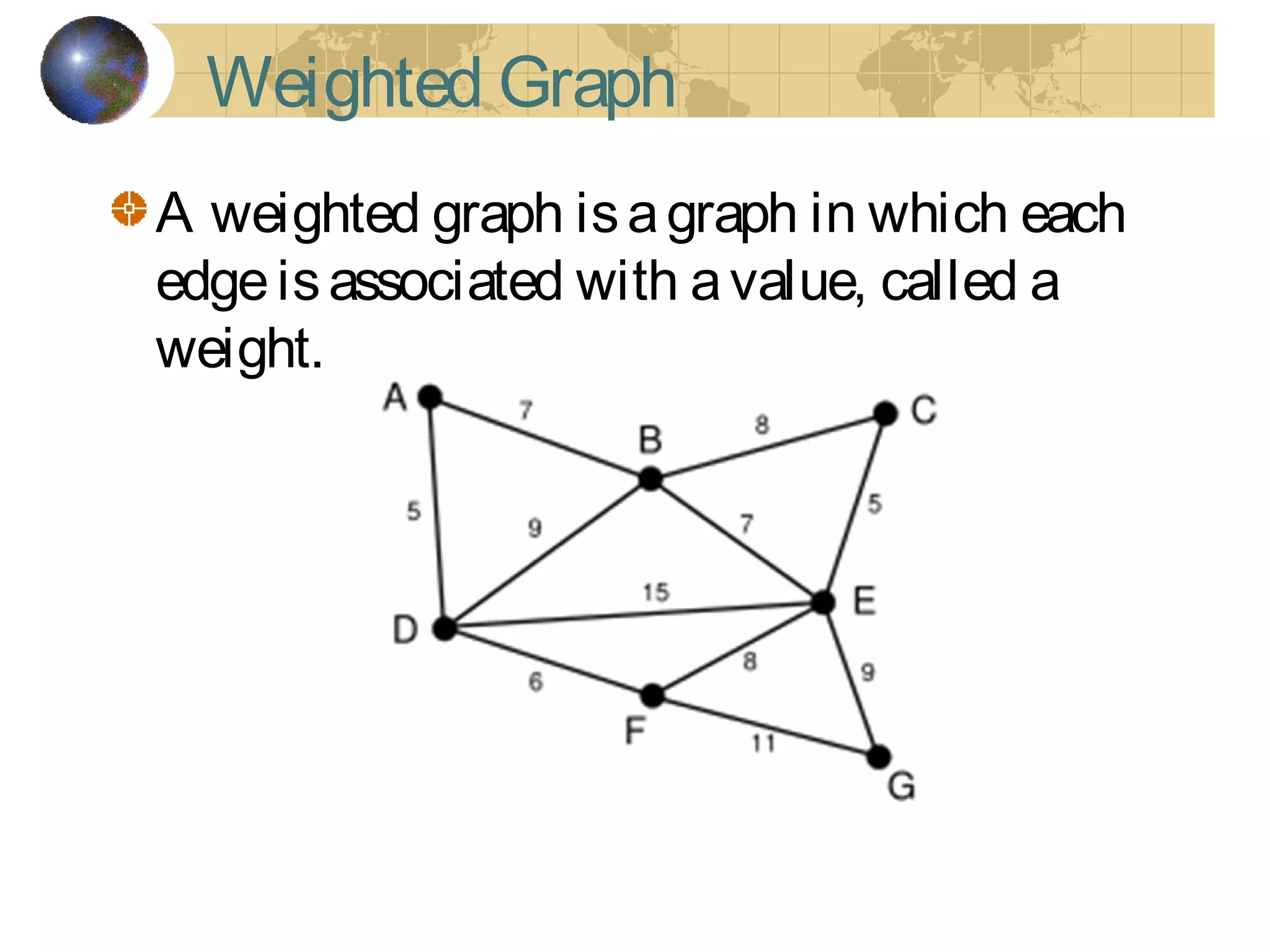
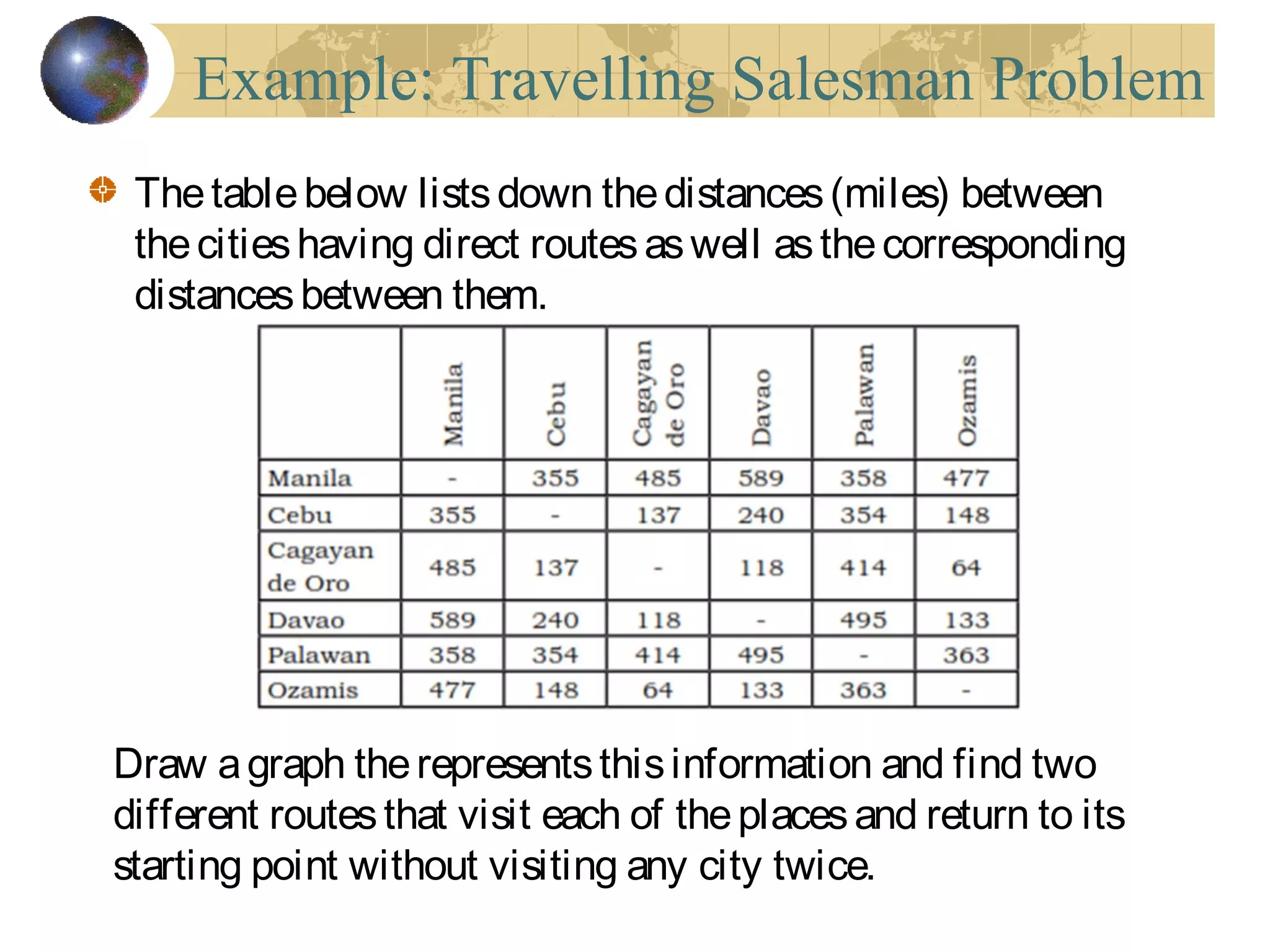
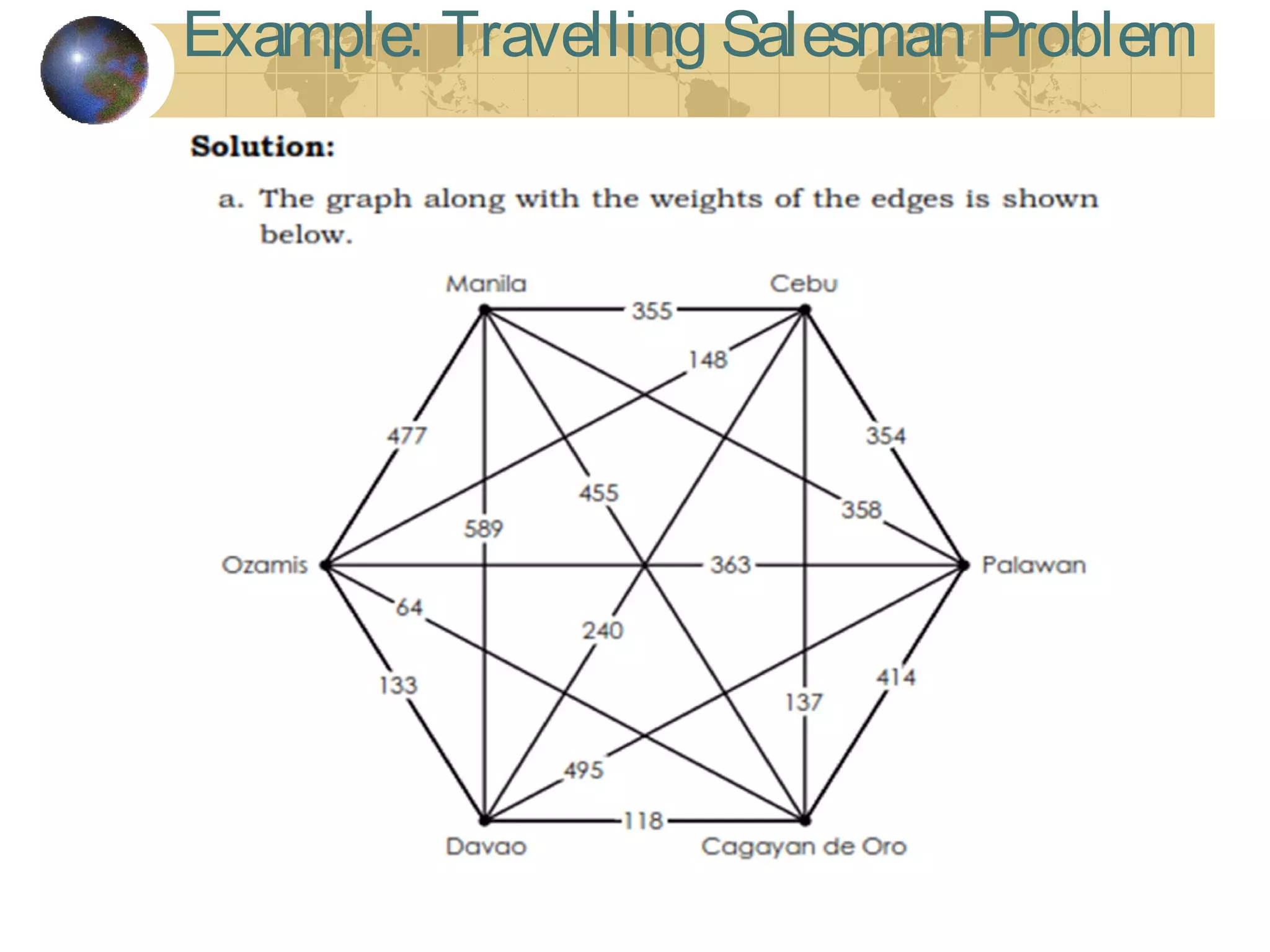
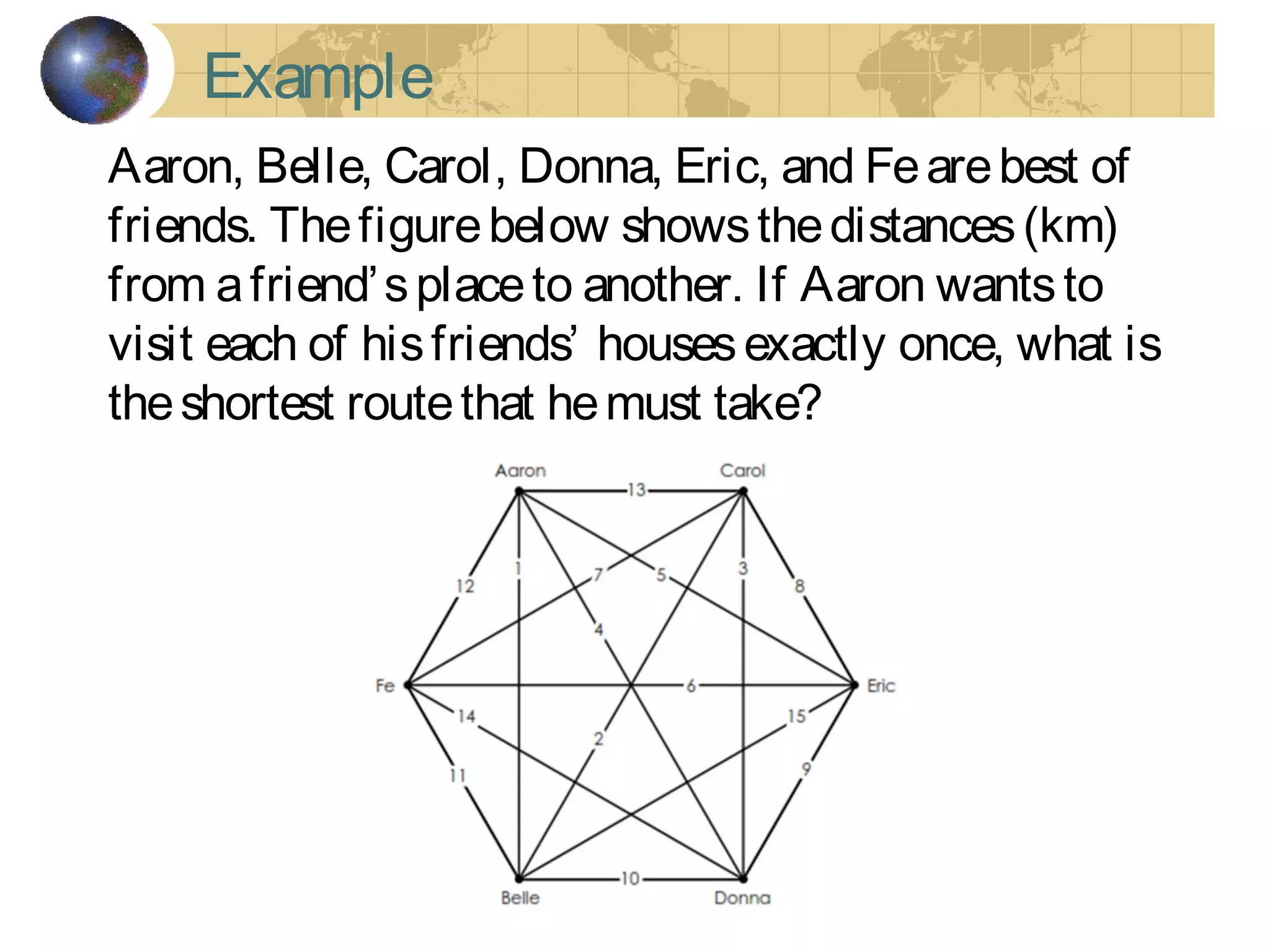
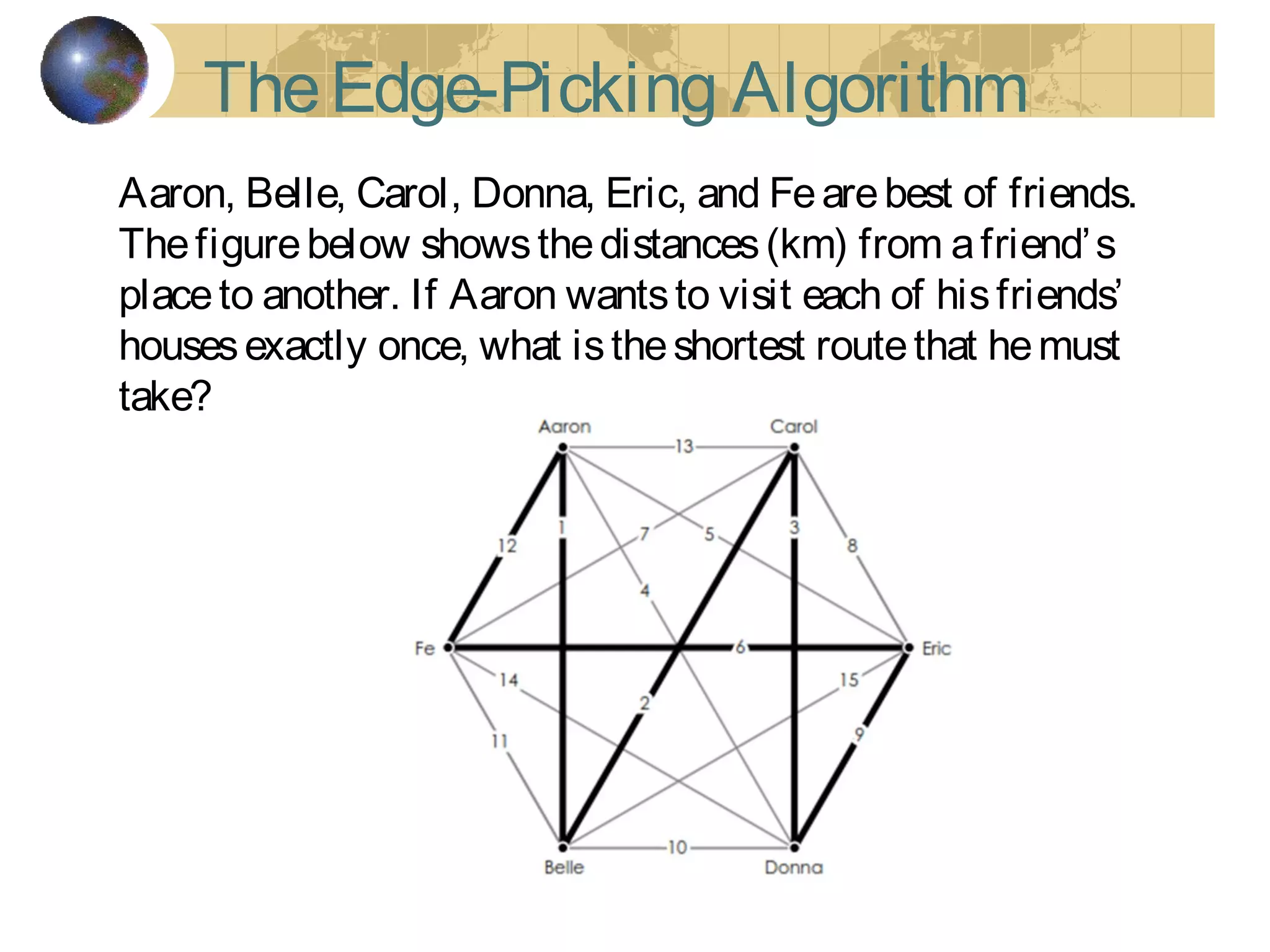
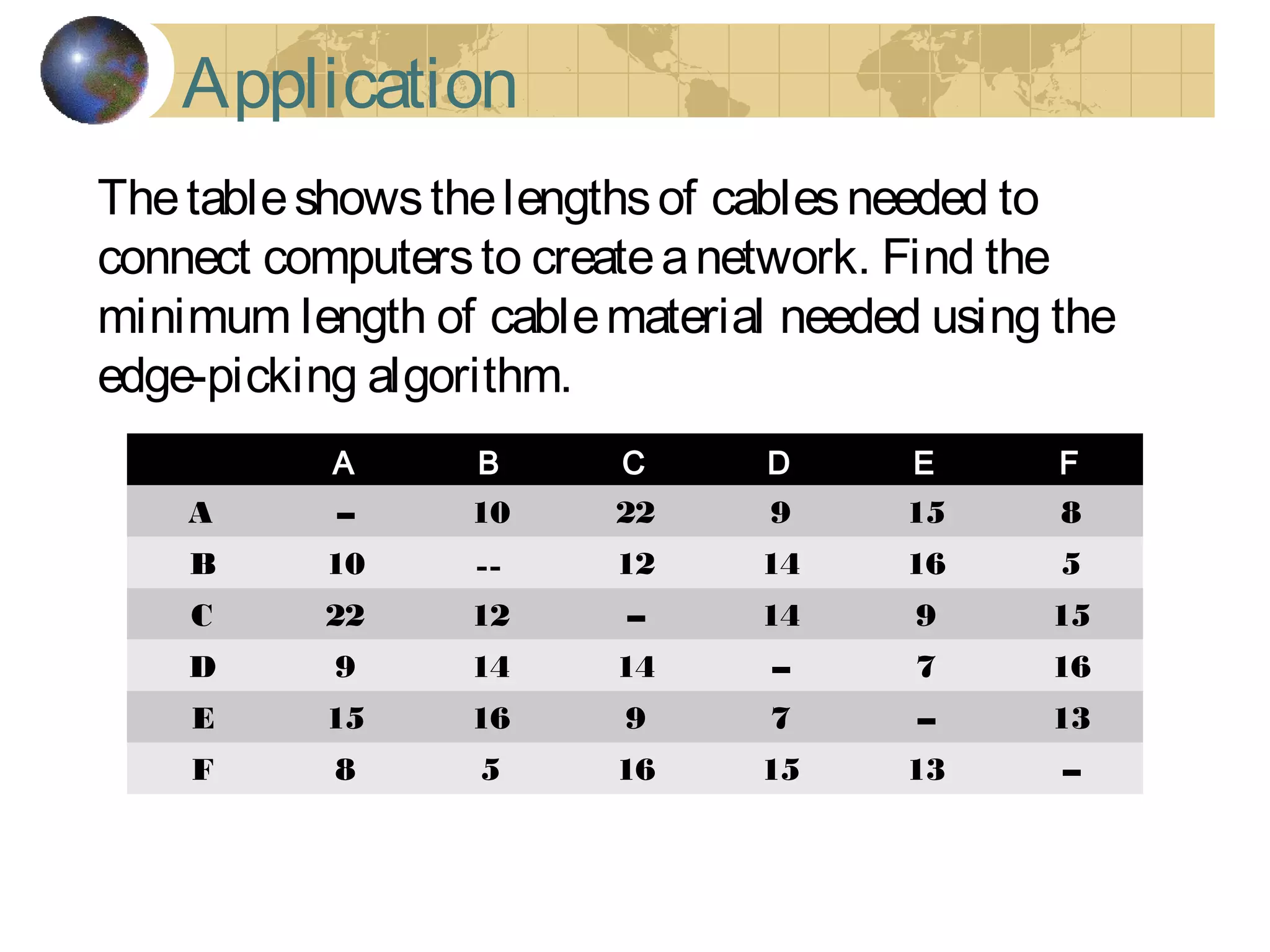
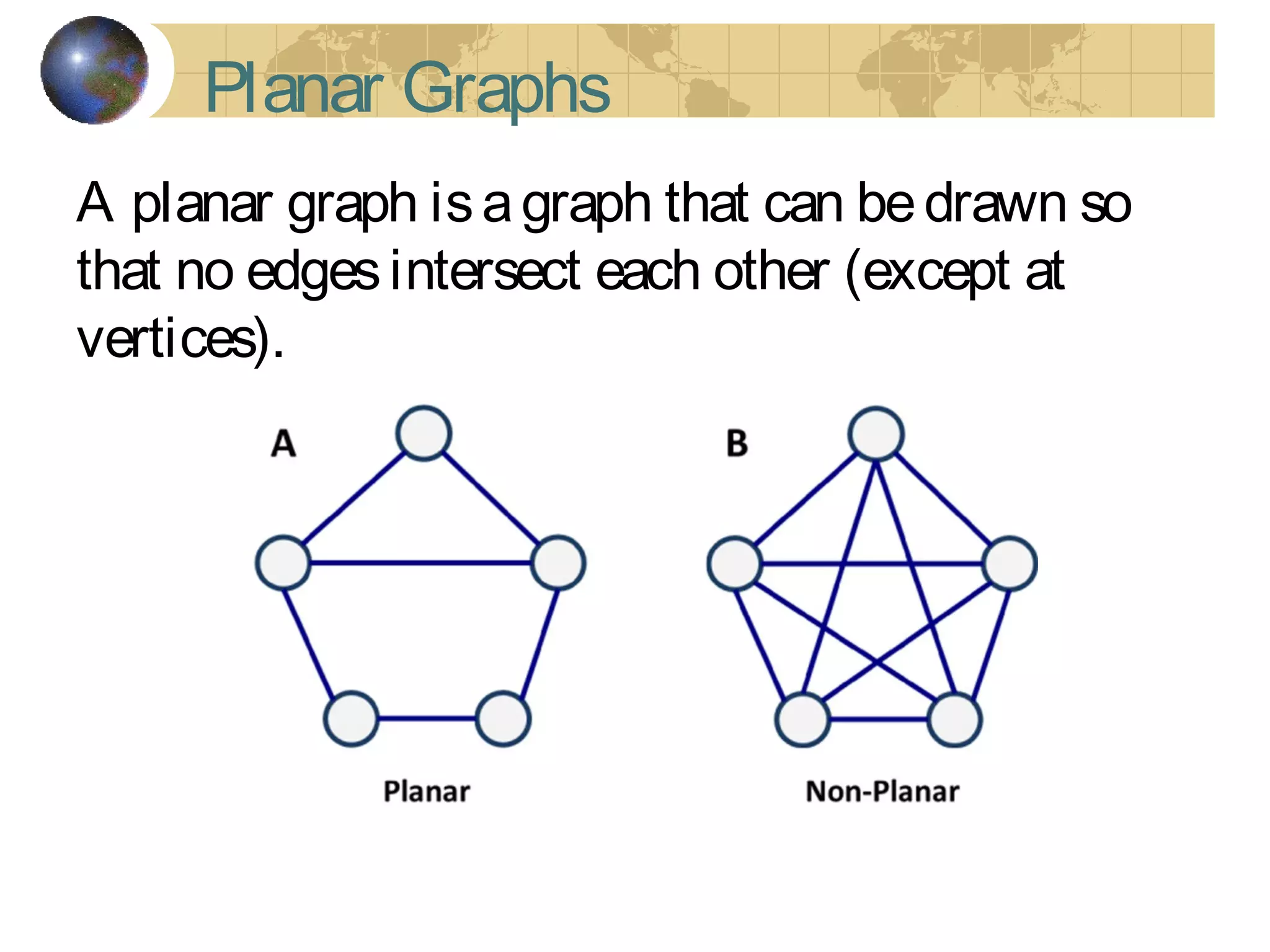
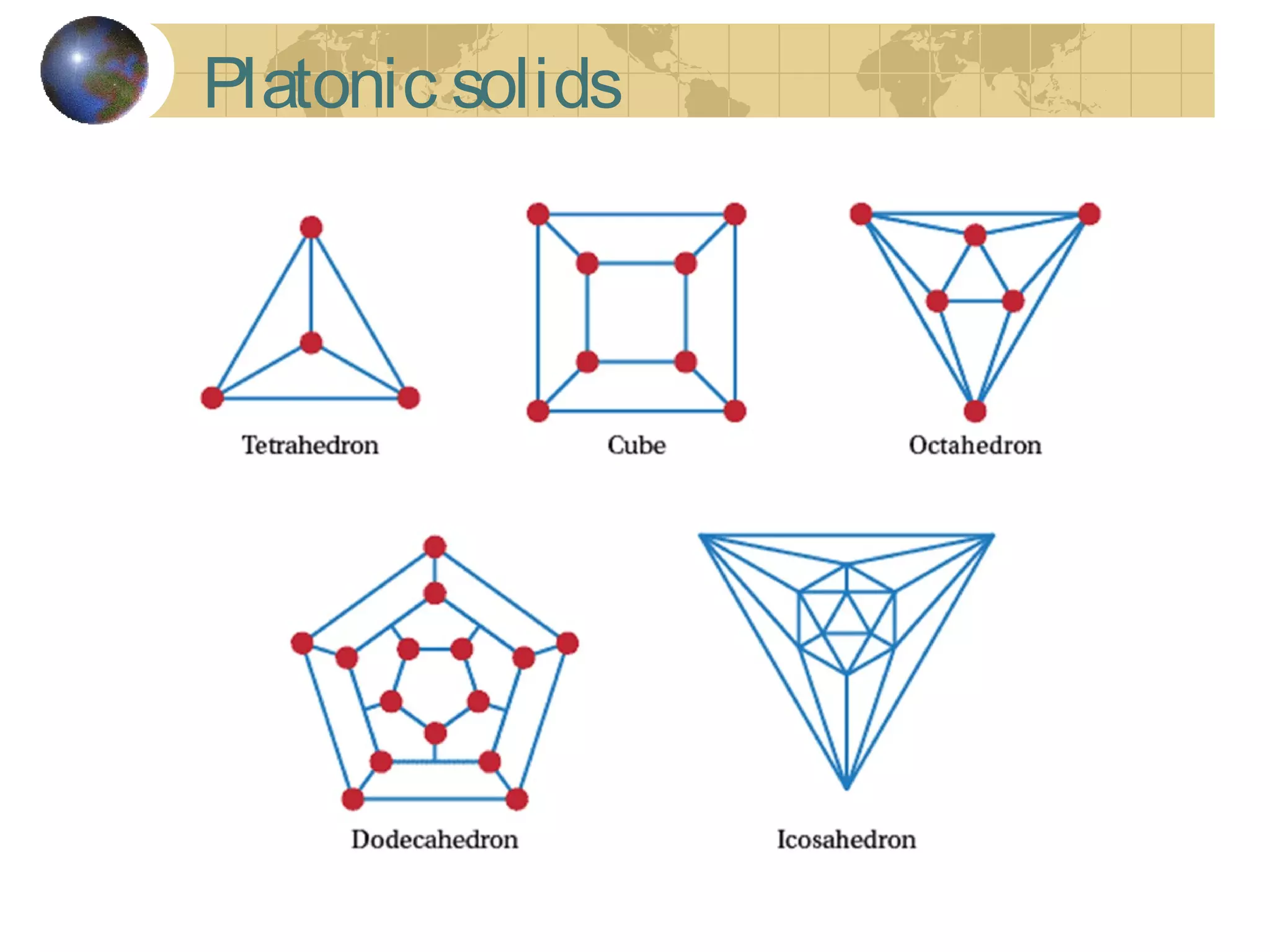
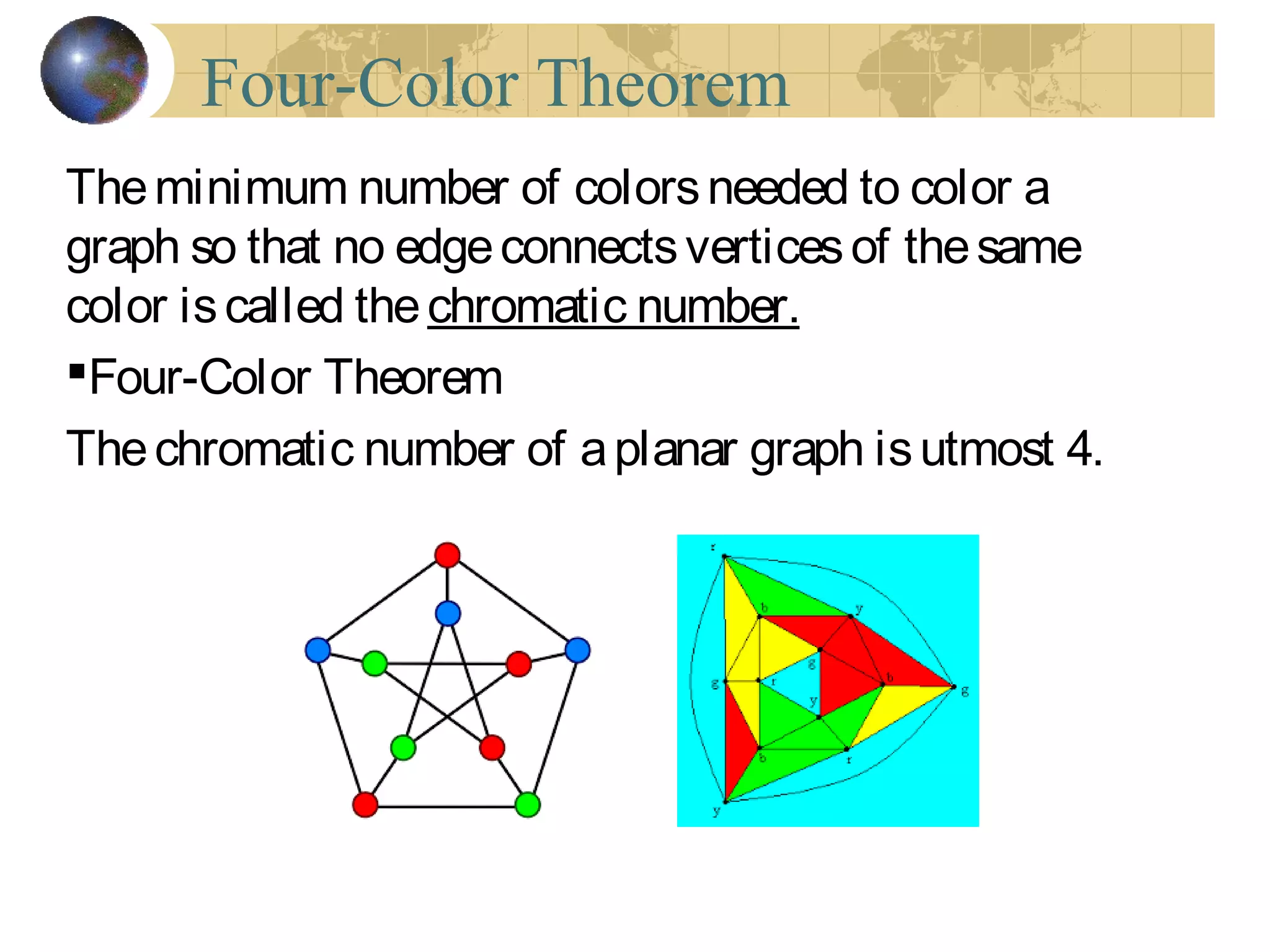
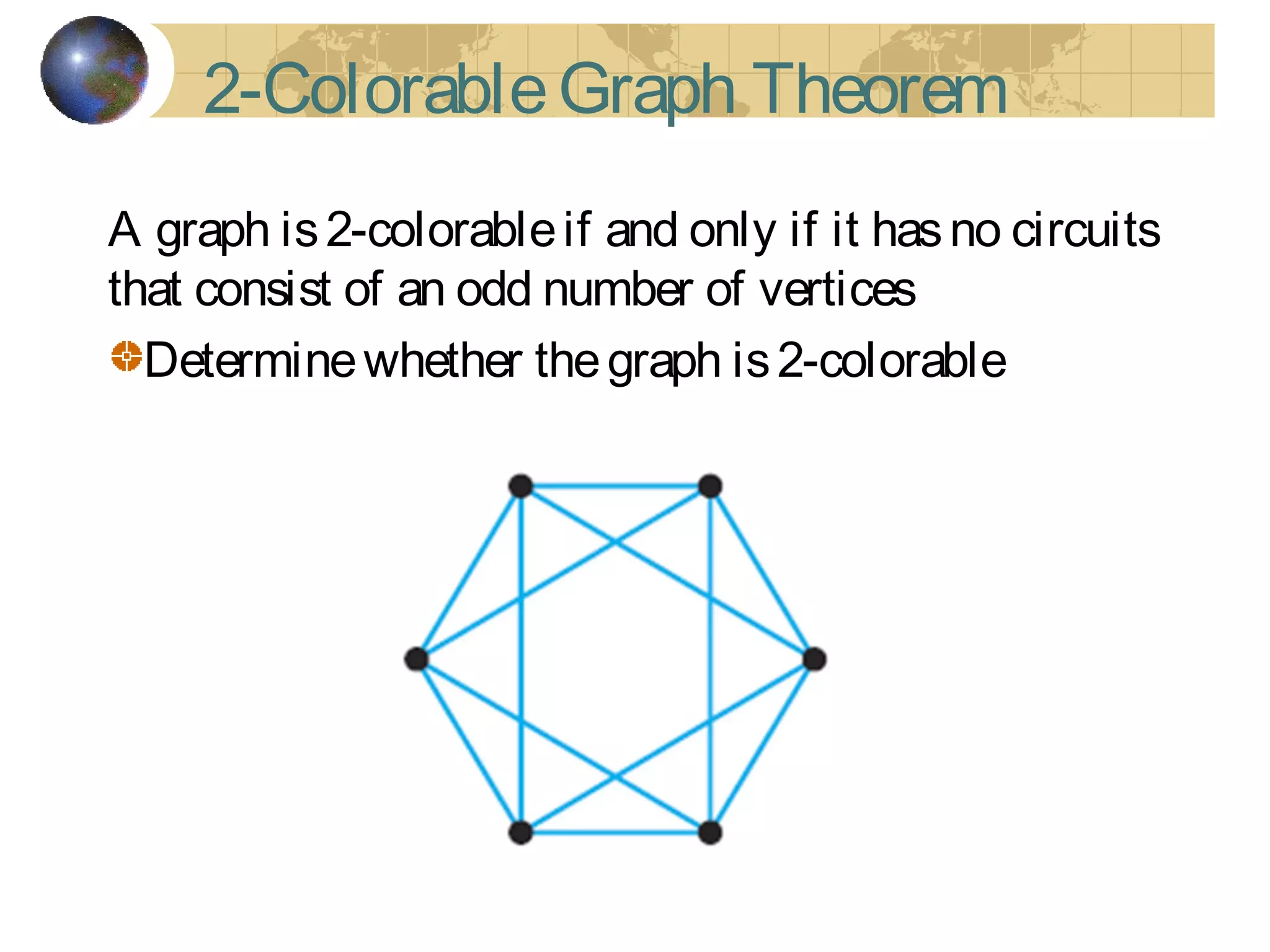
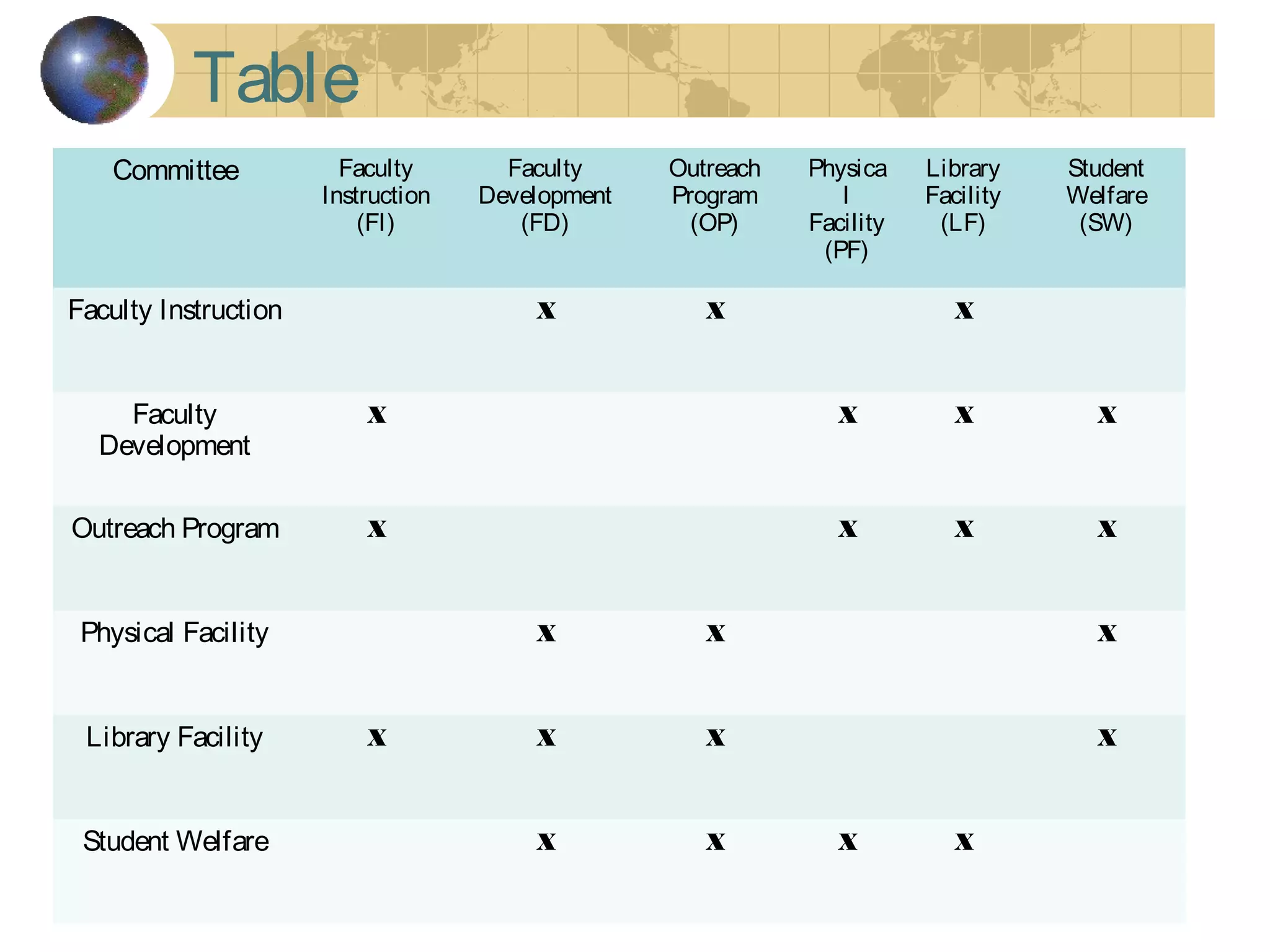
The document discusses Hamiltonian paths and circuits, defined as paths that visit each vertex exactly once, noting the lack of straightforward criteria for determining Hamiltonian circuits compared to Euler circuits. Dirac's theorem is introduced, which provides a condition for a graph to be Hamiltonian, along with examples such as applications in airline flight graphs and the Traveling Salesman Problem. Various algorithms, including greedy and edge-picking algorithms, are mentioned for finding Hamiltonian circuits, leading to practical applications in scheduling and network design.

1. Graphs: Hamiltonian Path
and Circuits
By Prof. Liwayway Memije-Cruz

2. Irish mathematician
who contributed to the
development of optics,
dynamics, and algebra
—in particular,
discovering thealgebra
of quaternions. His
work proved significant
for thedevelopment of
quantum mechanics.
William Rowan Hamilton

3. https://youtu.be/AamHZhAmR7o

4. Hamiltonian Path and Circuit
A Hamiltonian path isapath that visits
each vertex of thegraph exactly once.
A Hamiltonian circuit isapath that uses
each vertex of agraph exactly onceand
returnsto thestarting vertex. A graph that
containsaHamiltonian circuit iscalled
Hamiltonian.

5.  In Euler circuits, welooked at closed pathsthat use
every edgeexactly once, possibly visiting avertex
morethan once.
 In Hamiltonian circuits, welook at pathsthat visit
each vertex exactly once, possibly not passing
through someof theedges.
 But unliketheEuler circuit, wheretheEulerian
Graph Theorem isused to determinewhether it
containsan Euler circuit or not, wedo not havea
straightforward criterion to determinewhether or not
aHamiltonian circuit existsin agraph.

6. Finding Hamilton circuit

7. Determine whether the graph below is Hamiltonian
or not. If it is, find a Hamiltonian circuit. If it is not,
explain why?
Answer: A – B – C – E – D – F – G – A.

8. Dirac’s Theorem
https://www.youtube.com/watch?
v=OGh5JKso0y4

9. Dirac’s Theorem
Consider aconnected graph with at least threeverticesand no
multipleedges. Let n bethenumber of verticesin thegraph. If
every vertex hasdegreeof at least n/2, then thegraph must be
Hamiltonian.

10. Application of Hamiltonian Circuit
Thegraph below shows
theavailableflightsof a
popular
airline. An edgebetween
two verticesindicatesthat
there
isadirect flight between
thetwo cities. Determine
whether
thegraph isHamiltonian.
If it is, find aHamiltonian
circuit.

11. Solution
 Thereareten verticesin thegraph, and n/2 =5 . Now,
vertex Manilahas9 edges, Tokyo 5, Seoul 5, Taipei 6,
Hongkong 7, Macau 9, Ho Chi Minh 5, KualaLumpur 5,
and Singapore5. Using Dirac’stheorem, thegraph is
Hamiltonian.
 Thismeansthat thegraph containsacircuit that visitseach
vertex and return to itsstarting point without visiting a
vertex morethan once.
 By trial and error, oneHamiltonian circuit isManila–
Tokyo – Seoul – Taipei – Hongkong – Macau – Bangkok –
Ho Chi Minh – KualaLumpur – Singapore– Manila.

12. Remember:
If thegraph doesnot meet therequirements
of theDirac’sTheorem, it still might be
Hamiltonian.

13. Exercises:
(Aufmann) UseDirac’stheorem to verify that the
graph isHamiltonian. Then find aHamiltonian
circuit.

14. Weighted Graph
A weighted graph isagraph in which each
edgeisassociated with avalue, called a
weight.

15. Travelling Salesman Problem
The travelling salesman problem (TSP) asksthe
following question: "Given alist of citiesand the
distancesbetween each pair of cities, what isthe
shortest possibleroutethat visitseach city exactly
onceand returnsto theorigin city?“
Thetravelling salesman problem consistsof a
salesman and aset of cities. Thesalesman hasto
visit each oneof thecitiesstarting from acertain
one(e.g. thehometown) and returning to thesame
city. Thechallengeof theproblem isthat the
travelling salesman wantsto minimizethetotal
length of thetrip.

16. Example: Travelling Salesman Problem
Thetablebelow listsdown thedistances(miles) between
thecitieshaving direct routesaswell asthecorresponding
distancesbetween them.
Draw agraph therepresentsthisinformation and find two
different routesthat visit each of theplacesand return to its
starting point without visiting any city twice.

17. Example: Travelling Salesman Problem

18. Example: Travelling Salesman Problem

19. TheGreedy Algorithm
A method of finding aHamiltonian circuit in acomplete
weighted graph isgiven by thefollowing greedy algorithm.
1.Chooseavertex to start at, then travel along theconnected
edgethat hasthesmallest weight.
2.After arriving at thenext vertex, travel along theedgeof
smallest weight that connectsto avertex not yet visited.
Continuethisprocessuntil you havevisited all vertices.
3.Return to thestarting vertex.
Take Note:
Thegreedy algorithm attemptsto giveacircuit of
minimal total weight, although it doesnot always
succeed.

20. Example
Aaron, Belle, Carol, Donna, Eric, and Fearebest of
friends. Thefigurebelow showsthedistances(km)
from afriend’splaceto another. If Aaron wantsto
visit each of hisfriends’ housesexactly once, what is
theshortest routethat hemust take?

21. Solution

22. TheEdge-Picking Algorithm
Another method of finding aHamiltonian circuit in
acompleteweighted graph isgiven by the
following edge-picking algorithm.
1.Mark theedgeof smallest weight in thegraph.
2.Mark theedgeof thenext smallest weight in the
graph, aslong asit doesnot completeacircuit and
doesnot add athird marked edgeto asinglevertex.
3.Continuetheprocessuntil you can no longer mark
any edges. Then mark thefinal edgethat completes
theHamiltonian circuit.

23. TheEdge-Picking Algorithm
Aaron, Belle, Carol, Donna, Eric, and Fearebest of friends.
Thefigurebelow showsthedistances(km) from afriend’s
placeto another. If Aaron wantsto visit each of hisfriends’
housesexactly once, what istheshortest routethat hemust
take?

24. Solution
 First wemark thelinesegment from Aaron’shouseto Belle’s
house, of weight 1.
 Next wemark thesegment from Belle’sto Carol’shouse, of
weight 2, followed by Carol’sto Donna’shouse, of weight 3,
followed by Eric’sto Fe’shouse, of weight 6.
 Takenotethat wecannot mark thesegment from Eric’shouseto
Aaron’sbecauseit can completeacircuit. Also, wecannot mark
thesegment from Carol’sto Fe’shousebecauseit can makethe
third marked edgeon avertex.
 Finally to completethecircuit, wemark thelinesegment from
Fe’shouseback to Aaron’s.
 Thefinal Hamiltonian circuit, of total weight
1+2+3+6+9+12=33, isAaron’shouse– Belle’shouse– Carol’s
house– Donna’shouse– Eric’shouse– Fe’shouseand back to
Aaron’s.

25. Theedge-picking algorithm attempts
to giveacircuit of minimal total
weight, although it doesnot always
succeed.
Remember

26. Application
Thetableshowsthelengthsof cablesneeded to
connect computersto createanetwork. Find the
minimum length of cablematerial needed using the
edge-picking algorithm.
A B C D E F
A -- 10 22 9 15 8
B 10 -- 12 14 16 5
C 22 12 -- 14 9 15
D 9 14 14 -- 7 16
E 15 16 9 7 -- 13
F 8 5 16 15 13 --

27. Planar Graphs
A planar graph isagraph that can bedrawn so
that no edgesintersect each other (except at
vertices).

28. Platonic solids

29. Subgraphs
A part of agraph G iscalled asubgraph of G.
Subgraph Theorem
“If agraph G hasasubgraph that isnot planar, theG isalso not
planar. In particular, if containstheUtilitiesGraph or K5 asa
subgraph, G isnot planar.”
Nonplanar Graph Theorem
A graph isnonplanar if and only if it hastheUtilitiesGraph or
K5 asasubgraph, or it hasasubgraph that can becontracted to
theUtilitiesGraph or K5.

30. https://youtu.be/Cxdyh7A4-Ho
Euler’sFormula

31. Euler’sFormula
In aconnected planar graph drawn with no
intersecting edges, let v bethenumber of vertices, e
thenumber of edges, and f thenumber of faces.
Then v + f = e+ 2.

32. Graph Coloring
If themap isdivided into regionsin somemanner, what is
theminimum number of colorsrequired if theneighboring
regionsareto becolored differently?
Thereisaconnection between map coloring and graph
theory. Mapscan bemodeled by graphsusing the
countriesastheverticesand two vertices(countries) are
adjacent if they shareacommon boundary.
In graph coloring, each vertex of agraph will beassigned
onecolor in such away that no two adjacent verticeshave
thesamecolor. Theinteresting ideahereisto determine
theminimum number of (distinct) colorsto beused so that
wecan color each vertex of agraph with no two adjacent
verticeshavethesamecolor

33. Four-Color Theorem
Theminimum number of colorsneeded to color a
graph so that no edgeconnectsverticesof thesame
color iscalled thechromatic number.
Four-Color Theorem
Thechromatic number of aplanar graph isutmost 4.

34. 2-ColorableGraph Theorem
A graph is2-colorableif and only if it hasno circuits
that consist of an odd number of vertices
Determinewhether thegraph is2-colorable

35. Scheduling Problem
Six collegeaccreditation committeesneed to hold
meetingson thesameday, but someteachers
belong to morethan onecommittee. In order to
avoid membersmissing meetings, themeetings
need to bescheduled during different timeslots.
An “X” in thetableindicatesthat thetwo
corresponding committeesshareat least one
member. Usegraph coloring to determinethe
minimum number of timeslotsnecessary to
ensurethat all faculty memberscan attend all
meetings.

36. Table
Committee Faculty
Instruction
(FI)
Faculty
Development
(FD)
Outreach
Program
(OP)
Physica
l
Facility
(PF)
Library
Facility
(LF)
Student
Welfare
(SW)
Faculty Instruction X X X
Faculty
Development
X X X X
Outreach Program X X X X
Physical Facility X X X
Library Facility X X X X
Student Welfare X X X X

37. Solution
First wedraw agraph representing thesix committeesusing six
verticesor nodesin any configuration. An edgeconnectstwo
committeesthat shareat least onemember.
Then assign each vertex of thegraph with onecolor in such a
way that no two adjacent verticeshavethesamecolor.

38. Conclusion
Obviously, thegraph isnot 2-colorablebecausewe
can find circuitsof odd length but thegraph is3-
colorable. Hence, theminimum number of timeslots
necessary to ensurethat all faculty memberscan
attend all meetingsis3.
Scheduleof Meetings
First timeslot: Faculty Instruction, Student
Welfare
Second timeslot: Faculty Development,
Outreach
Program
Third timeslot: Library Facility, Physical Facility

39. References:
 https://www.coursera.org/lecture/discrete-mathematics/hamilton-c
 https://www.britannica.com/biography/William-Rowan-Hamilton
 http://math.gmu.edu/~tlim/DiracTheorem.pdf
Baltazar, Ethel CecilleM. Mathematicsin theModern World by C & E
Publishing Inc. 2018
Aufmann et al, Mathematical Excursions(2013)
Baltazar, Ethel CecilleM.
Mame, Neil (BatangasStateUniversity),
Manalang, Rodman (UE Manila),
Maquiling Rene(Xavier University),
Mocorro, Ronald (LeyteNormal University) – Powerpoint
Presentation (2017)