Kinematics

Dr. M.N. Shesha Prakash
Vice Principal, Head
Department of Civil Engineering
VVIET, Mysore

• Dynamics:
– Dynamics is the branch of science which deals with the study
of behavior of a body or particle in the state of motion under
the action of force system
• Dynamics branches into two streams called kinematics and
kinetics.
• Kinematics
– is the branch of dynamics which deals with the study of
properties of motion of the body or particle under the system
of forces without considering the effect of forces.
• Kinetics
– is the branch of dynamics which deals with the study of
properties of motion of the body or particle in such way that
the forces which cause the motion of body are mainly taken
into consideration.

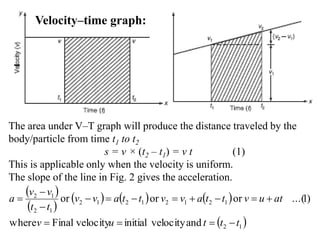
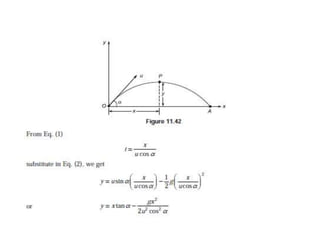
TECHNICAL TERMS RELATED TO MOTION
• Motion
• Path
• Displacement and Distance Travelled
• Velocity
– Average Velocity
– Instantaneous Velocity
– Speed
• Acceleration
– Average Acceleration
– Acceleration due to Gravity (g)

Newton’s Laws of Motion
• Newton’s first law:
– Every body continues in its state of rest or of uniform motion,
so long as it is under the influence of a balanced force system.
• Newton’s second law:
– The rate of change momentum of a body is directly proportional
to the impressed force and it takes place in the direction of force
acting on it.
• Newton’s third law:
– Action and reaction are equal in magnitude but opposite in
direction.
Types of Motion
Rectilinear motion
When a particle or a body moves along a straight line path, then
it is called linear motion or rectilinear motion.

• Curvilinear motion
– When a moving particle describes a path other than a straight
line is said be a particle in curvilinear motion.
• Projectile motion
– Whenever a particle is projected upwards with some inclination
to the horizontal (but not vertical), it travels in the air and
traces a parabolic path and falls on the ground point (target)
other than the point of projection
Rectilinear Motion
• When a particle or a body moves along a straight line path,
then it is called linear motion or rectilinear motion.
• Equation of motion along a straight line
– v = u + at
– v2 – u2 = 2as
– s = ut + ½ at2

Velocity–time graph:
The area under V–T graph will produce the distance traveled by the
body/particle from time t1 to t2
s = v × (t2 – t1) = v t (1)
This is applicable only when the velocity is uniform.
The slope of the line in Fig. 2 gives the acceleration.
 
 
     
 12
12121212
12
12
andvelocityinitialvelocityFinalwhere
)1...(ororor
tttuv
atuvttavvttavv
tt
vv
a






As seen from earlier graph, the total distance travelled is given by the
area under the curve and hence the area is given as
 
 
 
1
2
12
121
at timevelocityinitialtheisWhere
2
2
1
get,weng,Substituti
onacceleratiBut
2
1
tu
atuts
t
vv
a
tvvtvs




From Eqs (1) and (2), eliminating t, we get
 32or2222
2
1
22222
2
asuvuvuvuuvas
a
uv
a
a
uv
us






 





 


Problems on Rectilinear Motion
The motion of a particle is given by the equation x = t3 – 3t2 – 9t + 12.
Determine the time, distance travelled and acceleration of particle when
velocity becomes zero.
Solution:
Differentiating Eq. (1) with respect to ‘x’, we get
and the solution is
t = –1 or t = 3 s (negative value of t can be discarded)
t = 3 s
Substitute t = 3 s in (1), we get
x = –15 m
 2963 2
 tt
dt
dx
v
 11293 23
 tttx
0963:0when 2
 ttv
2
2
2
m/s1263666  t
dt
xd
a

2. The acceleration of a particle is defined by a = –2 m/s2, if v = 8 m/s
and x = 0 when t = 0. Determine (i) Velocity (ii) Distance travelled at t
= 6 s.
Solution: We know that
a = –2 m/s2
a = dv/dt
dv = adt
dv = –2dt (1)
Integrating Eq. (1), we get
v = –2t + C
at v = 8 m/s
t = 0
8 = –2 × 0 + C
C = 8
v = –2t + 8 (2)

From (2)
v = –2t + 8
dx/dt = v
dx = vdt
dx = (–2t + 8)dt (3)
Integrating Eq. (2), we get
x = -2t2/2 + 8t + K
x = –t2 + 8t + K
at x = 0, t = 0, K = 0
x = –t2 + 8t (4)
Substitute t = 6 s in (2) and (4), we get

3. A driver of a car travelling at a speed of 72 km/h observes the light 300
m ahead of him turning red. The traffic light is timed to remain red for
20 s before it turns to green. If the motorist wishes to pass the light
without stopping to wait for it to green. Determine (i) Required uniform
acceleration of car (ii) The speed with which the motorist crosses the
traffic light.
(i) Uniform acceleration: We know that t = 20 s
m/s20
6060
100072



u
    222
m/s5.0or20
2
1
2020300or
2
1
 aaatuts
m/s10205.020  atuv

4. A motorist starts with initial velocity takes 10 s to cover a distance
of 20 m and 15 s to cover a distance of 40 m. Find the uniform
acceleration of car and the velocity at the end of 15 s.
 
 1501020
10
2
1
1020bygivenis10sintravelledDistance
2
1
thatknowWe
2
2
au
au
atuts



 
 25.1121540
15
2
1
1540bygivenis15sintravelledDistance
2
au
au


Solving Eqs. 1 and 2, we get a = 0.267m/s2 and u = 0.664m/s
m/s669.415267.0664.0
bygivenis15sofendat theVelocity


v
atuv

5. A car is moving with a velocity of 15 m/s. The car
is brought to rest by applying brakes in 5 s.
Determine (i) Retardation (ii) Distance travelled
by the car after applying the brakes.

6. A car and truck are both travelling at a
constant speed of 45 km/h. Car is 10 m behind
the truck. The truck driver suddenly applies his
brakes, causing the truck to decelerate at a
constant rate at 2 m/s2. Two seconds later the
driver of car applied his brakes and just
manages to avoid rear end collision. Determine
the constant rate at which the car decelerated.

7. The acceleration of a particle is defined by the relation
a = (32 – 6t2). The particle starts at t = 0 with v = 0
and x = 50 m. Determine (a) Time when the velocity is
again zero (b) Position and velocity when t = 6 s (c)
The total distance travelled by the particle from t = 0 s
to t = 6 s.

MOTION UNDER GRAVITY
• When a body is allowed to fall freely, it is acted upon
by acceleration due to gravity and its velocity goes on
increasing until it reaches the ground.
• The force of attraction of the earth that pulls all bodies
towards the centre of earth with uniform acceleration is
known as Acceleration due to Gravity.
• The value of acceleration due to gravity is constant in
general and its value is considered to be 9.81 m/s2 and
is always directed towards the centre of earth.
Acceleration due to gravity is generally denoted by ‘g’.
• When the body is moving vertically downwards, the
value of g is considered as positive and if the body is
projected vertically upwards, then acceleration due to
gravity is considered as negative.

Evidently, all equations of motion are applicable except by replacing
uniform acceleration ‘a’
with acceleration due to gravity ’g’and are written as
(i) When a body is projected vertically downward, under the action of
gravity, the equations of motion are
v = u + gt
v2 = u2 + 2gh
h = ut + ½ gt2
(ii) When a body is projected vertically upward, under the action of
gravity, the equations of motion are
v = u – gt
v2 = u2 – 2gh
h = ut – ½ gt2

1. A ball is thrown vertically upward into air with an initial
velocity of 35 m/s. After 3 s another ball is thrown
vertically. What initial velocity must be the second ball has
to pass the first ball at 30 m from the ground.

1. A stone is dropped into a well and a sound of splash is heard after 4 s. Find
the depth of well if the velocity of sound is 350 m/s.

2. A stone is dropped from the top of the tower 50 m high. At the same
time another stone is thrown up from the foot of the tower with a
velocity of 25 m/s. At what distance from the top and after how much
time the two stones cross each other.

3. A stone is thrown vertically into the air from the top of tower 100 m
high. At the same instant a second stone is thrown upward from the
ground. The initial velocity of first stone is 50 m/s and that of
second stone is 75 m/s. When and where will the stones be at the
same height from the ground.

PROJECTILES
Whenever a particle is projected upwards with some
inclination to the horizontal (but not vertical), it travels
in the air and traces a parabolic path and falls on the
ground point (target) other than the point of projection.
The particle itself is called projectile and the path
traced by the projectile is called trajectory

Terms used in projectile
1. Velocity of projection (u): It is the velocity with
which projectile is projected in the upward direction
with some inclination to the horizontal.
2. Angle of projection (α): It is the angle with which the
projectile is projected with respect to horizontal.
3. Time of flight (T): It is the total time required for the
projectile to travel from the point of projection to the
point of target.
4. Horizontal range (R): It is the horizontal distance
between the point of projection and target point.
5. Vertical height (h): It is the vertical distance/height
reached by the projectile from the point of projection.

Time Of Flight:
Let T be the time of flight. We know that the
vertical ordinate at any point on the path of
projectile after a time T is given by

Let a particle be projected upward from a point O at an angle with horizontal with an initial
velocity of u m/s
Motion of projectile:
The vertical component of velocity is always affected by acceleration due to gravity. The
particle will reach the maximum height when vertical component becomes zero. The
horizontal component of velocity will remains constant since there is no effect of
acceleration due to gravity.
The combined effect of horizontal and vertical components of velocity will move the
particle along some path in air and then fall on the ground other than the point of
projection.

Problems on projections
1. A particle is projected at an angle of 60° with horizontal. The horizontal range
of particle is 5 km. Find (i) Velocity of projection (ii) Maximum height attained by the
particle

2. A particle is projected in air with a velocity of 100 m/s at an
angle of 30° with horizontal. Find the horizontal range,
maximum height attained and time of flight.
Solution : Data given: u = 100 m/s, g = 9.81 m/s2 and α= 30°
To find: R, T and hmax

3. A bullet is fired upwards at an angle of 30° to the horizontal from a point P
on a hill and it strikes a target which is 80 m lower than B. The initial velocity
of bullet is 100 m/s.
Calculate
(a) The maximum height with which the bullet will rise above the
horizontal
(b) The actual velocity with which it strikes the target
(c) The total time required for the flight of bullet
Neglect the air resistance.

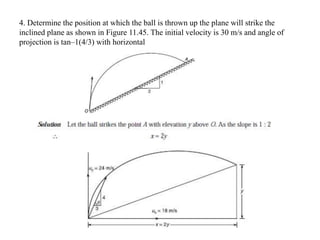
4. Determine the position at which the ball is thrown up the plane will strike the
inclined plane as shown in Figure 11.45. The initial velocity is 30 m/s and angle of
projection is tan–1(4/3) with horizontal

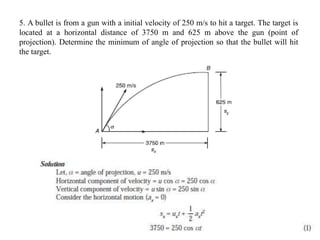
5. A bullet is from a gun with a initial velocity of 250 m/s to hit a target. The target is
located at a horizontal distance of 3750 m and 625 m above the gun (point of
projection). Determine the minimum of angle of projection so that the bullet will hit
the target.

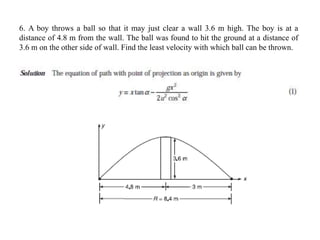
6. A boy throws a ball so that it may just clear a wall 3.6 m high. The boy is at a
distance of 4.8 m from the wall. The ball was found to hit the ground at a distance of
3.6 m on the other side of wall. Find the least velocity with which ball can be thrown.

Kinematics

More Related Content

What's hot

Similar to Kinematics

Recently uploaded

Kinematics