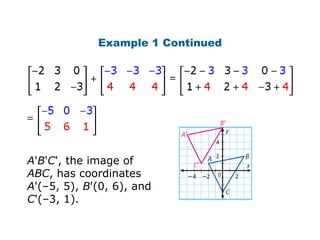
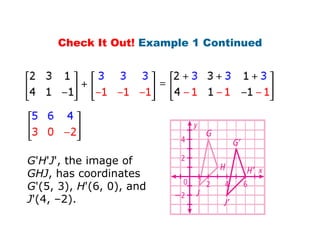
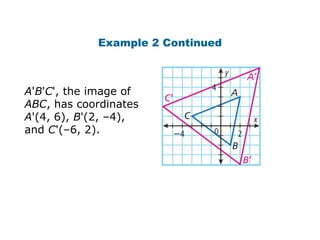
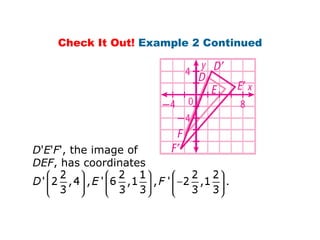
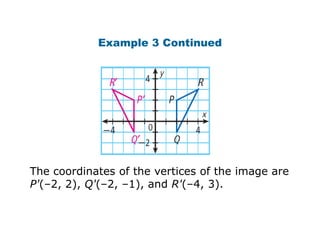
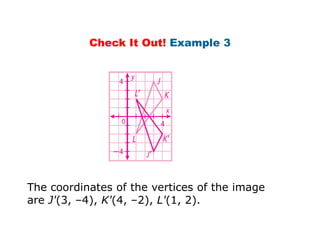
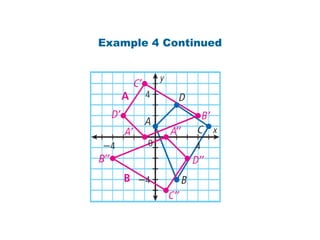
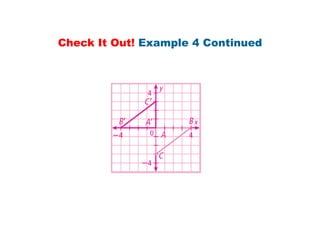
Using matrices to transform geometric figures, including translations, dilations, reflections, and rotations. Translations use a matrix with the distances of movement in each row. Dilations multiply coordinates by a scalar factor. Reflections across an axis involve changing the sign of coordinates on one side of the axis. Rotation matrices involve trigonometric functions to rotate the figure a specified number of degrees clockwise or counterclockwise. Examples show setting up and performing each type of transformation on sample polygons.

2. Using Matrices to Transform
Geometric Figures
Warm Up
Lesson Presentation
Lesson Quiz

3. Warm Up
Perform the indicated operation.
1.
2.
3.

4. Objective
Use matrices to transform a plane
figure.

5. Vocabulary
translation matrix
reflection matrix
rotation matrix

6. You can describe the position, shape, and size of a
polygon on a coordinate plane by naming the
ordered pairs that define its vertices.
The coordinates of ΔABC below are A (–2, –1),
B (0, 3), and C (1, –2) .
You can also define ΔABC by a matrix:
 x-coordinates
 y-coordinates

7. A translation matrix is a matrix used to
translate coordinates on the coordinate plane.
The matrix sum of a preimage and a translation
matrix gives the coordinates of the translated
image.

8. Reading Math
The prefix pre- means ―before,‖ so the preimage
is the original figure before any transformations
are applied. The image is the resulting figure
after a transformation.

9. Example 1: Using Matrices to Translate a Figure
Translate ΔABC with coordinates A(–2, 1),
B(3, 2), and C(0, –3), 3 units left and 4 units
up. Find the coordinates of the vertices of
the image, and graph.
The translation
matrix will have –3  x-coordinates
in all entries in row  y-coordinates
1 and 4 in all entries
in row 2.

10. Example 1 Continued
A'B'C', the image of
ABC, has coordinates
A'(–5, 5), B'(0, 6), and
C'(–3, 1).

11. Check It Out! Example 1
Translate ΔGHJ with coordinates G(2, 4), H(3,
1), and J(1, –1) 3 units right and 1 unit down.
Find the coordinates of the vertices of the image
and graph.
The translation
matrix will have 3 in  x-coordinates
all entries in row 1  y-coordinates
and –1 in all entries
in row 2.

12. Check It Out! Example 1 Continued
G'H'J', the image of
GHJ, has coordinates
G'(5, 3), H'(6, 0), and
J'(4, –2).

13. A dilation is a transformation that scales—enlarges
or reduces—the preimage, resulting in similar
figures. Remember that for similar figures, the
shape is the same but the size may be different.
Angles are congruent, and side lengths are
proportional.
When the center of dilation is the origin,
multiplying the coordinate matrix by a scalar gives
the coordinates of the dilated image. In this
lesson, all dilations assume that the origin is the
center of dilation.

14. Example 2: Using Matrices to Enlarge a Figure
Enlarge ΔABC with coordinates
A(2, 3), B(1, –2), and C(–3, 1), by a factor
of 2. Find the coordinates of the vertices of
the image, and graph.
Multiply each coordinate by 2 by multiplying each
entry by 2.
 x-coordinates
 y-coordinates

15. Example 2 Continued
A'B'C', the image of
ABC, has coordinates
A'(4, 6), B'(2, –4),
and C'(–6, 2).

16. Check It Out! Example 2
Enlarge ΔDEF with coordinates D(2, 3), E(5,
1), and F(–2, –7) a factor of . Find the
coordinates of the vertices of the image, and
graph.
Multiply each coordinate by by multiplying each
entry by .

17. Check It Out! Example 2 Continued
D'E'F', the image of
DEF, has coordinates

18. A reflection matrix is a matrix that creates a
mirror image by reflecting each vertex over a
specified line of symmetry. To reflect a figure
across the y-axis, multiply
by the coordinate matrix. This reverses the x-
coordinates and keeps the y-coordinates
unchanged.

19. Caution
Matrix multiplication is not commutative. So be
sure to keep the transformation matrix on the
left!

20. Example 3: Using Matrices to Reflect a Figure
Reflect ΔPQR with coordinates
P(2, 2), Q(2, –1), and R(4, 3) across the
y-axis. Find the coordinates of the
vertices of the image, and graph.
Each x-coordinate is multiplied by –1.
Each y-coordinate is multiplied by 1.

21. Example 3 Continued
The coordinates of the vertices of the image are
P'(–2, 2), Q'(–2, –1), and R'(–4, 3).

22. Check It Out! Example 3
To reflect a figure across the x-axis, multiply by
.
Reflect ΔJKL with coordinates J(3, 4), K(4, 2),
and L(1, –2) across the x-axis. Find the
coordinates of the vertices of the image and
graph.

23. Check It Out! Example 3
The coordinates of the vertices of the image
are J'(3, –4), K'(4, –2), L'(1, 2).

24. A rotation matrix is a matrix used to rotate a
figure. Example 4 gives several types of rotation
matrices.

25. Example 4: Using Matrices to Rotate a Figure
Use each matrix to rotate polygon ABCD
with coordinates A(0, 1), B(2, –
4), C(5, 1), and D(2, 3) about the origin.
Graph and describe the image.
A.
The image A'B'C'D' is rotated 90° counterclockwise.
B.
The image A''B''C''D'' is rotated 90° clockwise.

26. Example 4 Continued

27. Check It Out! Example 4
Use
Rotate ΔABC with coordinates A(0, 0),
B(4, 0), and C(0, –3) about the origin.
Graph and describe the image.
A'(0, 0), B'(-4, 0), C'(0, 3); the image is rotated
180°.

28. Check It Out! Example 4 Continued

29. Lesson Quiz
Transform triangle PQR with vertices
P(–1, –1), Q(3, 1), R(0, 3). For each, show
the matrix transformation and state the
vertices of the image.
1. Translation 3 units to the left and 2 units up.
2. Dilation by a factor of 1.5.
3. Reflection across the x-axis.
4. 90° rotation, clockwise.

30. Lesson Quiz
1.
2.
3. 4.