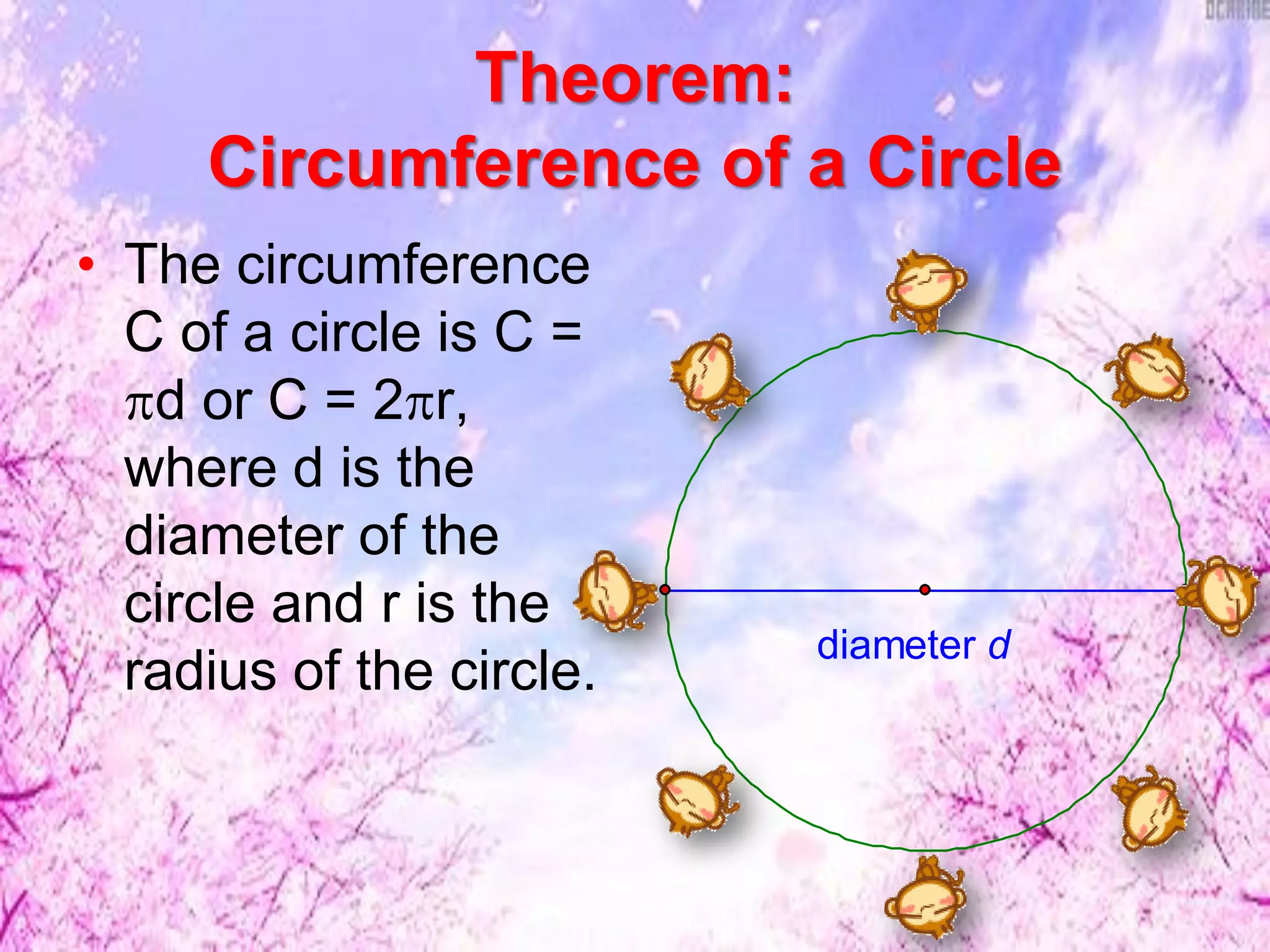
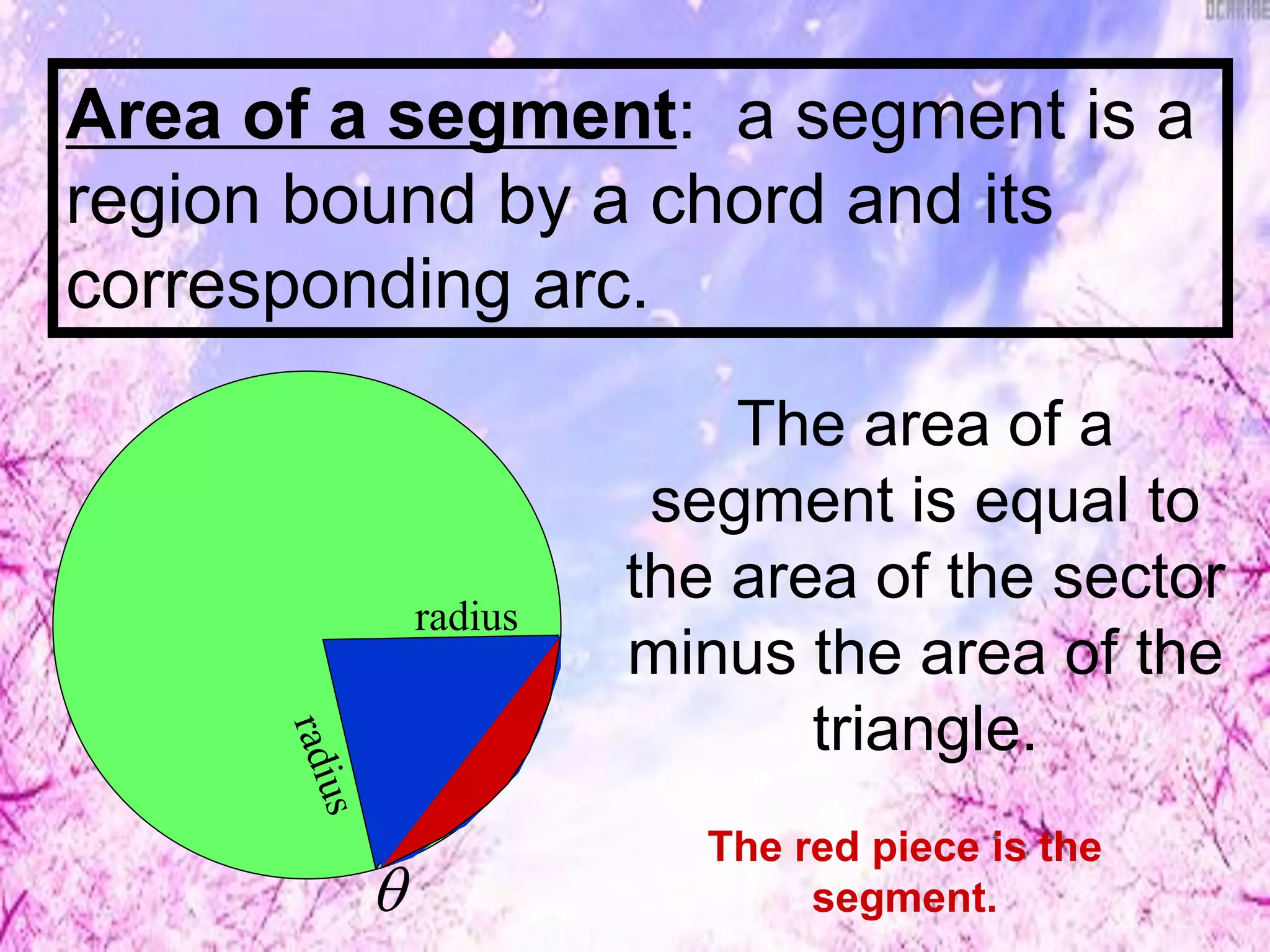
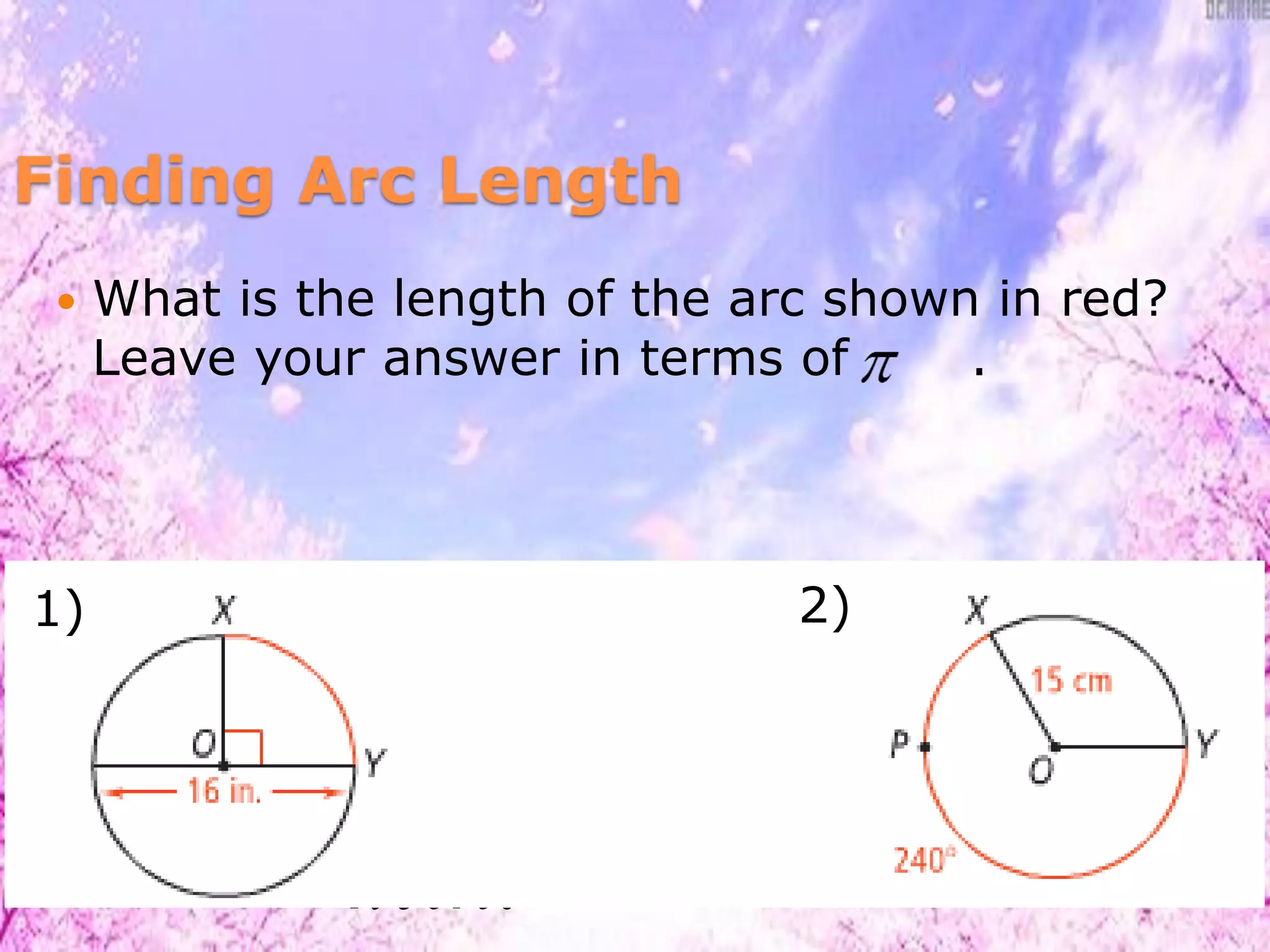
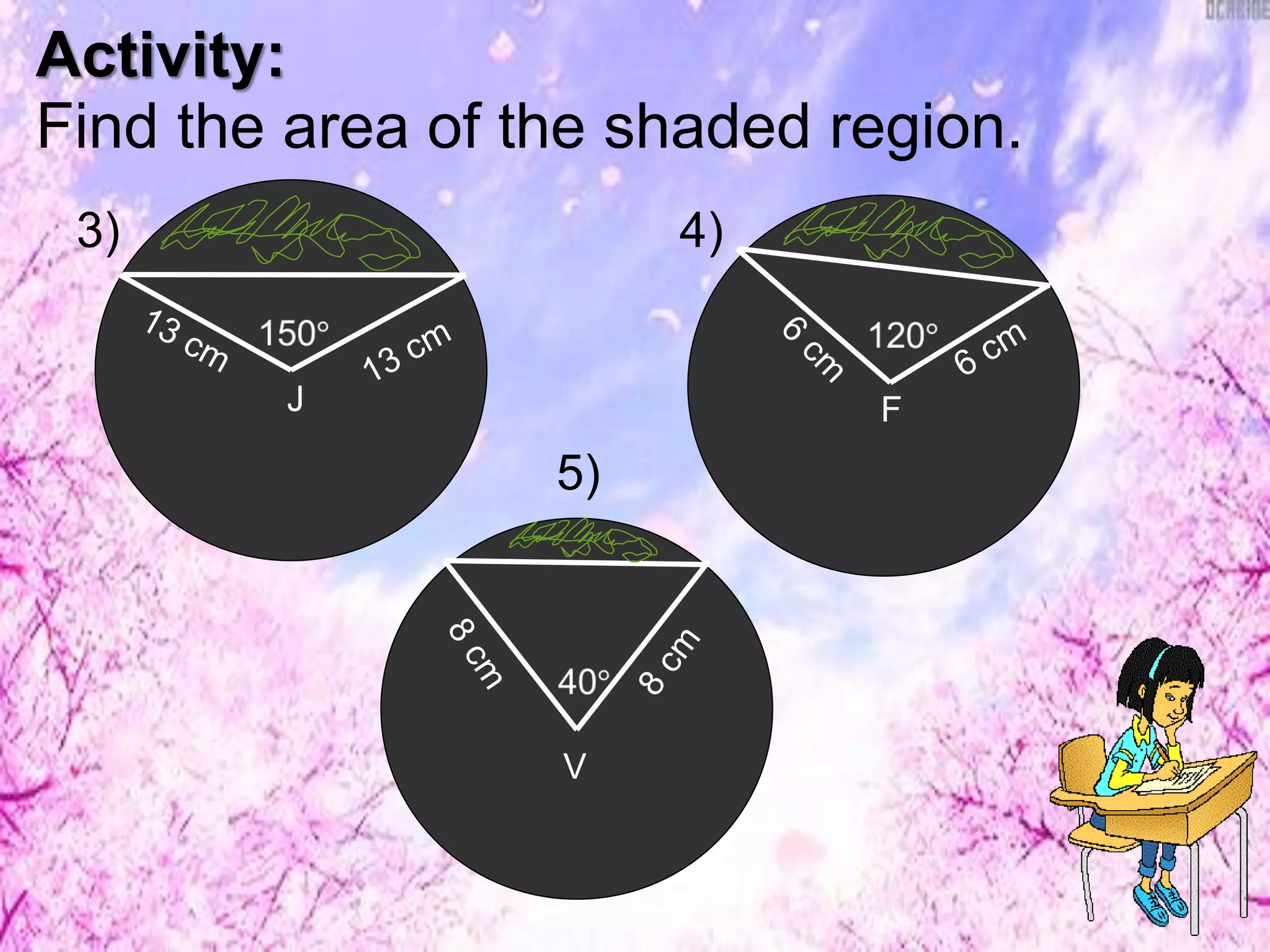
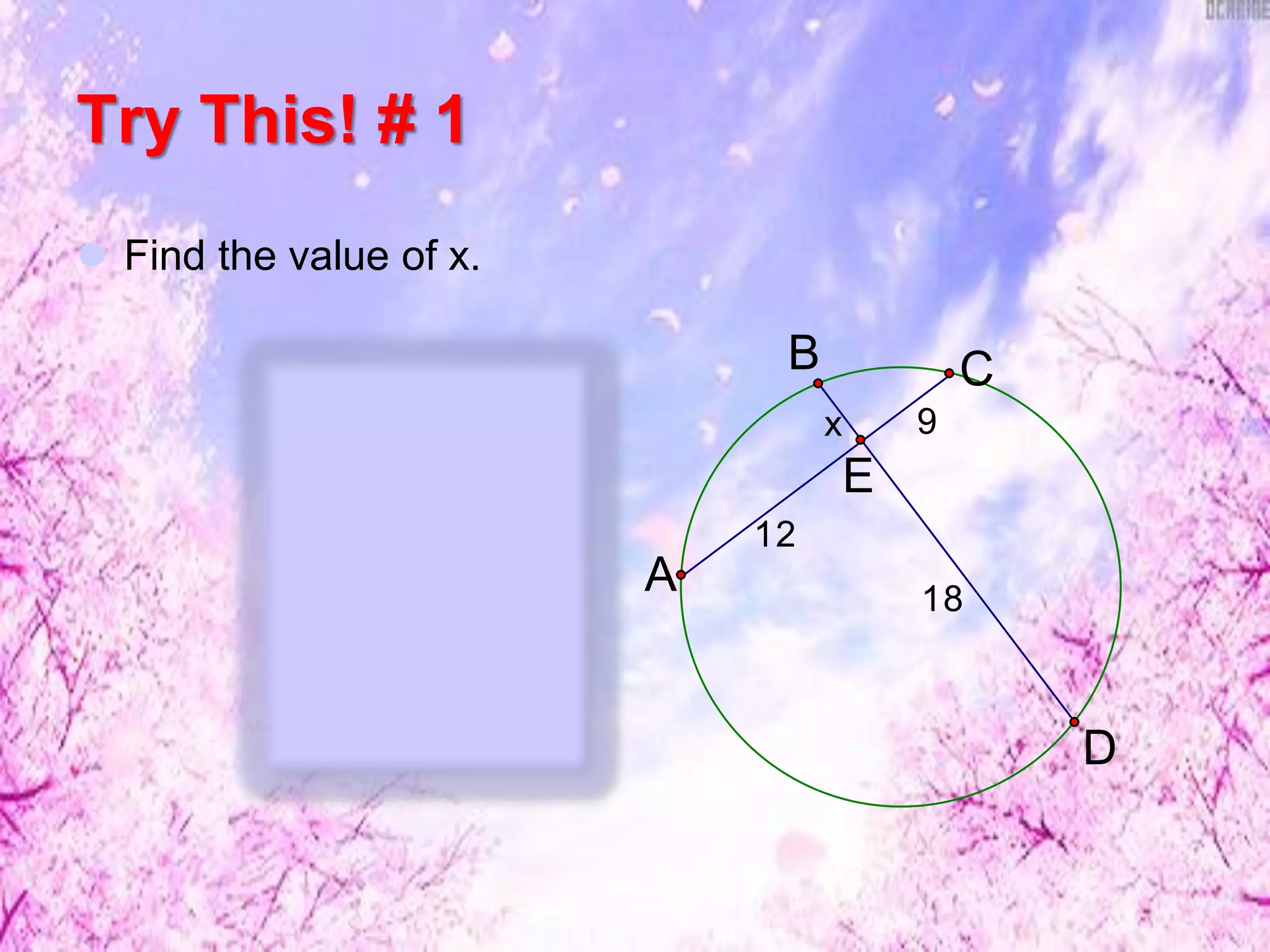
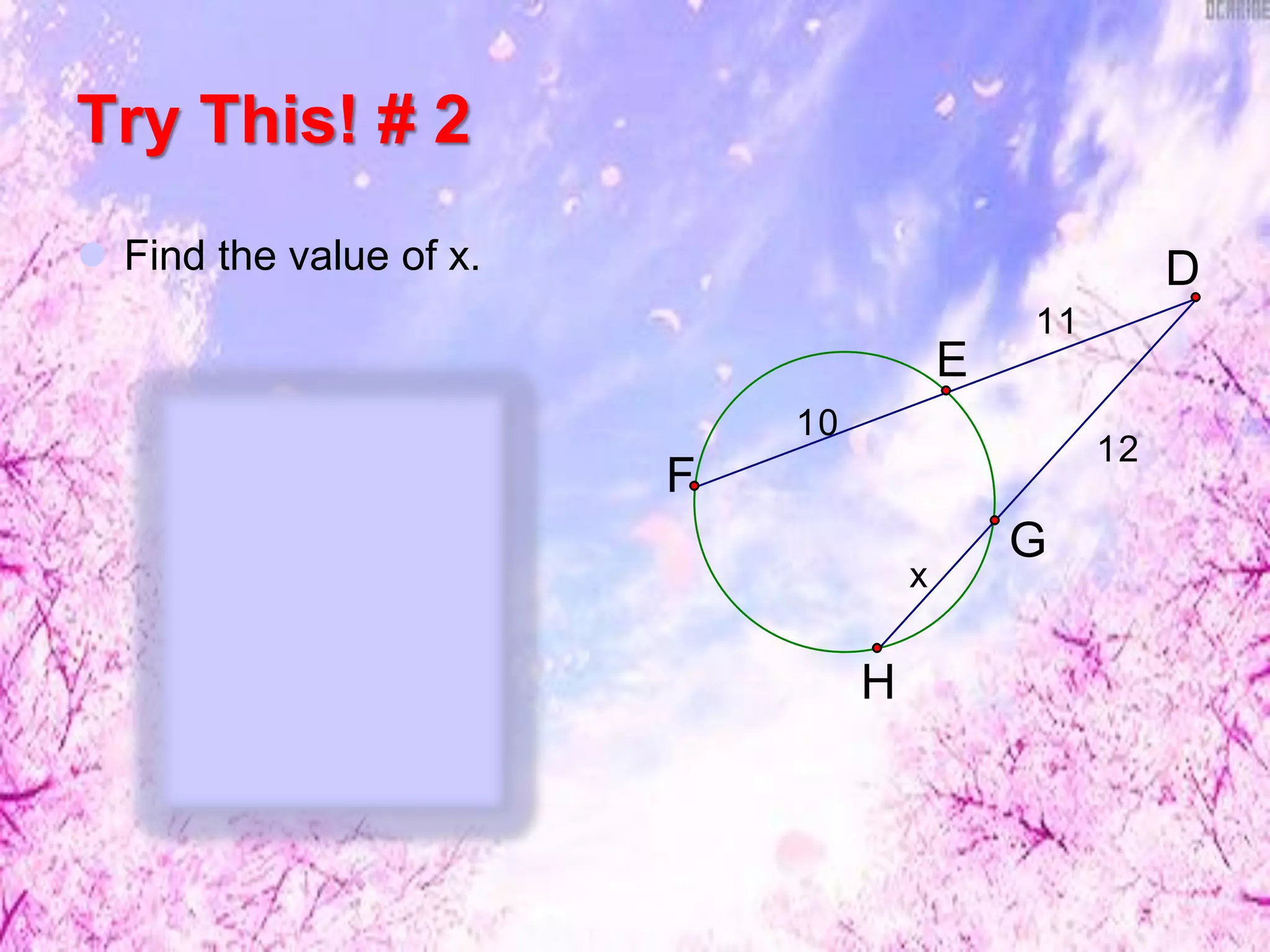
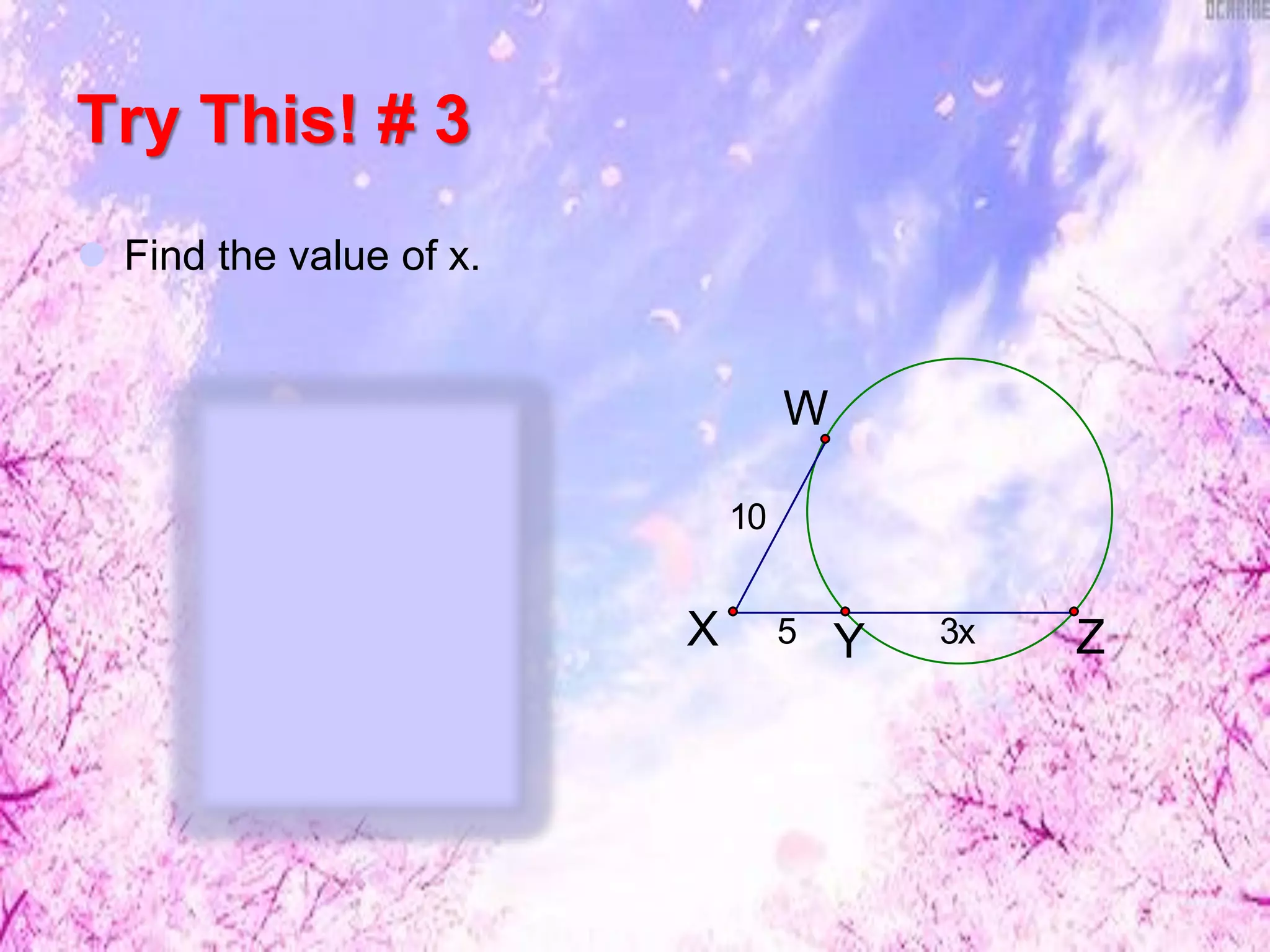
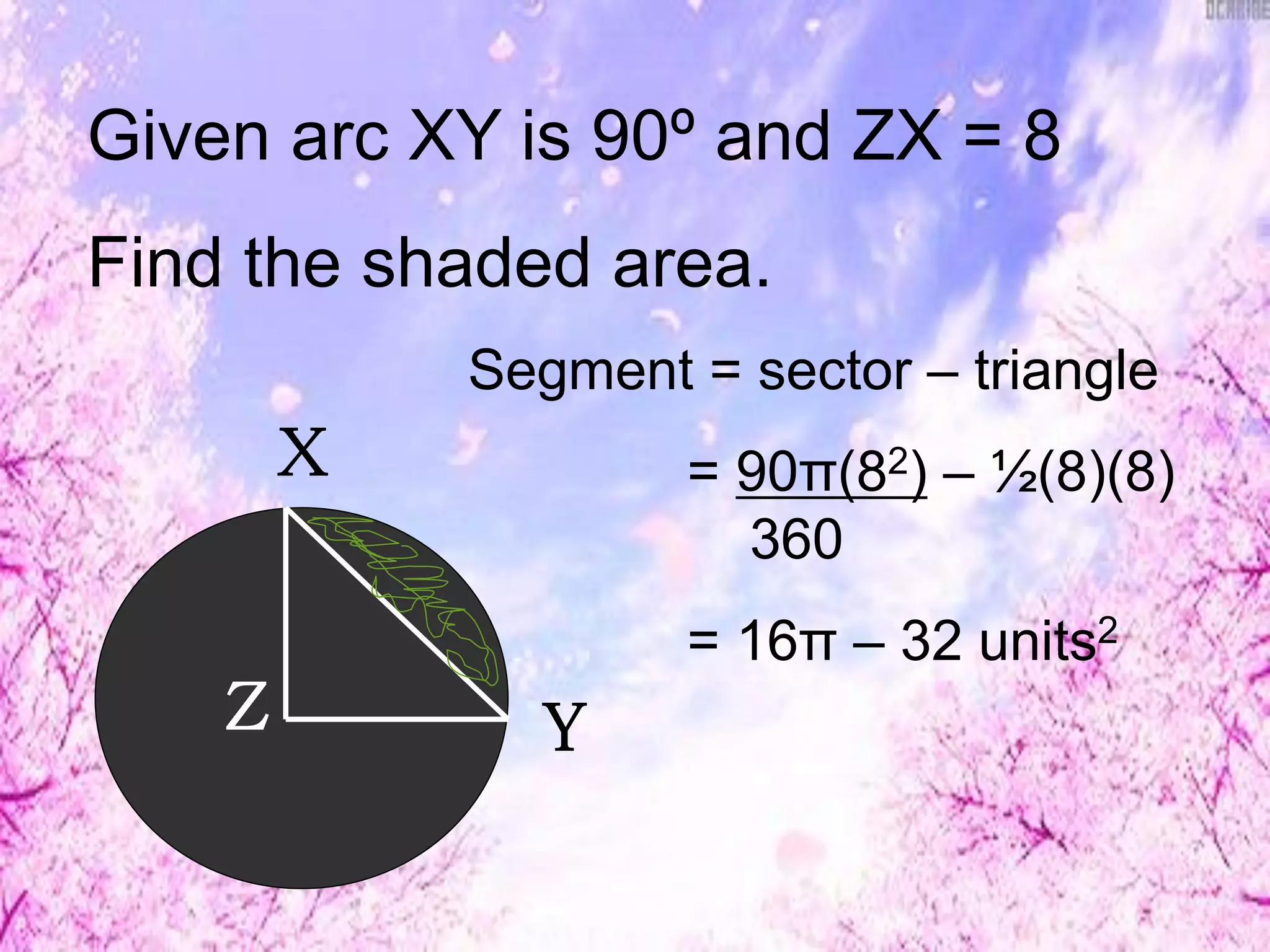This document discusses finding lengths of arcs, chords, segments, and circumferences in circles. It defines circumference as 2πr and arc length as (degree measure of arc/360) × 2πr. Examples show calculating circumference, arc length, and using theorems like chord-product and secant-tangent to find unknown segment lengths. The key ideas are that circumference is proportional to diameter/radius and arc length is proportional to its central angle measure. Various geometry problems demonstrate applying these circle concepts.

2. Objectives
Find the circumference of a circle and
the length of a circular arc.
Use circumference and arc length to
solve real-life problems.
Find the area of a sector and a segment
in a circle.
Find the lengths of segments of chords.
Find the lengths of segments of
tangents and secants.

3. Finding circumference and arc
length
• The circumference of a circle is the
distance around the circle. For all
circles, the ratio of the circumference
to the diameter is the same. This
ratio is known as  or pi.

4. Theorem:
Circumference of a Circle
• The circumference
C of a circle is C =
d or C = 2r,
where d is the
diameter of the
circle and r is the
radius of the circle.
diameter d

5. Ex. 1: Using circumference
• Find (a) the circumference of a circle
with radius 6 centimeters and (b) the
radius of a circle with circumference
31 meters. Round decimal answers
to two decimal places.

6. Solution:
C = 2r
= 2 •  • 6
= 12
 37.70
So, the
circumference is
about 37.70 cm.
C = 2r
31 = 2r
31 = r
4.93  r
So, the radius is
about 4.93 cm.
2
a.
b.

7. And . . .
• An arc length is a portion of the
circumference of a circle. You can
use the measure of an arc (in
degrees) to find its length (in linear
units).

8. Ex. 2: Finding Arc Lengths
• Find the length of each arc.
5 cm
B
A
50°
a.
7 cm
D
C
50°
b. 7 cm
F
E
100°
c.

9. Arc Length Corollary
• In a circle, the ratio
of the length of a
given arc to the
circumference is
equal to the ratio of
the measure of the
arc to 360°. AB
Arc length of
2r
=
360°
or Arc length of =
360°
• 2r
m AB

AB
m

10. More . . .
• The length of a
semicircle is half the
circumference, and
the length of a 90°
arc is one quarter of
the circumference.
½ • 2r
r
¼ • 2r
r
r

11. Ex. 2: Finding Arc Lengths
• Find the length of each arc.
5 cm
B
A
50°
a.
a. Arc length of =AB
 50°
360°
• 2(5)
a. Arc length of =AB
 # of °
360°
• 2r
 4.36 centimeters

12. Ex. 2: Finding Arc Lengths
• Find the length of each arc.
7 cm
D
C
50°
b. b. Arc length of =CD
 # of °
360°
• 2r
b. Arc length of =CD
 50°
360°
• 2(7)
 6.11 centimeters

13. Ex. 2: Finding Arc Lengths
• Find the length of each arc.
7 cm
F
E
100°
c. c. Arc length of =
# of °
360°
• 2r
c. Arc length of =EF
 100°
360°
• 2(7)
EF

 12.22 centimeters
In parts (a) and (b) in Example 2, note that the
arcs have the same measure but different
lengths because the circumferences of the
circles are not equal.

14. Ex. 3: Using Arc Lengths
• Find the indicated measure.
3.82 m
R
Q
P
60°
a. circumference PQ
Arc length of
2r =
PQ
m
360°
3.82
2r 6
1
=
3.82
2r 360°
60°
=
3.82(6) = 2r
22.92 = 2r
C = 2r; so using substitution, C = 22.92
meters.

15. Ex. 3: Using Arc Lengths
• Find the indicated measure.
XY
b. m XY
Arc length of
2r = 360°
18
2(7.64) 360°
=
135°  m
XY
m
XY
m
• 360°360° •
XY

So the m 
135°
XY
7.64 in.
18 in.
Z
Y
X

16. Ex. 4: Comparing Circumferences
• Tire Revolutions: Tires
from two different
automobiles are shown
on the next slide. How
many revolutions does
each tire make while
traveling 100 feet?
Round decimal answers
to one decimal place.

17. • Reminder: C = d or
2r.
• Tire A has a diameter
of 14 + 2(5.1), or 24.2
inches.
• Its circumference is
(24.2), or about 76.03
inches.
Ex. 4: Comparing Circumferences

18. • Reminder: C = d or
2r.
• Tire B has a diameter
of 15 + 2(5.25), or 25.5
inches.
• Its circumference is
(25.5), or about 80.11
inches.
Ex. 4: Comparing Circumferences

19. Ex. 5: Finding Arc Length
a. Find the distance around Lane 1.
 The track is made up of two semicircles and two
straight sections with length s. To find the total
distance around each lane, find the sum of the
lengths of each part. Round decimal answers to
one decimal place.

20. • Divide the distance traveled by the tire
circumference to find the number of revolutions
made. First, convert 100 feet to 1200 inches.
TIRE A: 100 ft.
76.03 in.
1200 in.
76.03 in.= 100 ft.
80.11 in.
1200 in.
80.11 in.=
 15.8 revolutions
TIRE B:
 15.0 revolutions
Ex. 4: Comparing Circumferences

21. Ex. 5: Finding Arc Length
• Track. The track shown has six lanes. Each
lane is 1.25 meters wide. There is 180° arc at
the end of each track. The radii for the arcs in
the first two lanes are given.
a. Find the distance around Lane 1.
b. Find the distance around Lane 2.

22. • Distance = 2s + 2r1
= 2(108.9) + 2(29.00)
 400.0 meters
• Distance = 2s + 2r2
= 2(108.9) + 2(30.25)
 407.9 meters
Ex. 5: Lane 1
Ex. 5: Lane 2

24. A = r2
Definition of the Area of a Sector: a
region bound by 2 radii and an arc.
O
As you remember,
the area of a circle is
radius


25. Theorem: A sec = (mHP) r2
360
Where r is the radius and the arc
HP is measured in degrees.
Find the area, leave in terms of .
12m
60º
A = 60π(122)
360
A = 24π m2

26. Area of a segment: a segment is a
region bound by a chord and its
corresponding arc.
The area of a
segment is equal to
the area of the sector
minus the area of the
triangle.
radius

The red piece is the
segment.

27. X
YZ
Given arc XY is 90º and ZX = 8
Find the shaded area.
Segment = sector – triangle
= 90π(82) – ½(8)(8)
360
= 16π – 32 units2

28. ..Areas of Circles, Sectors &
Segments.mp4

29.  What is the length of the arc shown in red?
Leave your answer in terms of .
360
mXY
lengthof XY d 
90
(16)
360
 
4 .in
2
360
mXPY
lengthof XPY r 
240
2 (15)
360
 
20 cm
1) 2)

30. J F
V
Find the area of the shaded region.
Activity:
3) 4)
5)

31. Finding the Lengths of Chords
• When two chords intersect in the
interior of a circle, each chord is
divided into two segments which are
called segments of a chord. The
following theorem gives a relationship
between the lengths of the four
segments that are formed.

32. Chord Product Theorem
• If two chords
intersect in the
interior of a circle,
then the product of
the lengths of the
segments of one
chord is equal to
the product of the
lengths of the
segments of the
other chord.
E
A
B
C
D
EA • EB = EC • ED

33. Proving the Chord Product
Theorem
• You can use similar
triangles to prove Theorem
10.15.
• Given: , are chords
that intersect at E.
• Prove: EA • EB = EC • ED
AB CD
E
D
B
C
A

34. Paragraph proof: Draw
and . Because C and
B intercept the same arc,
C  B. Likewise, A 
D. By the AA Similarity
Postulate, ∆AEC  ∆DEB.
So the lengths of
corresponding sides are
proportional.
AC
DB
E
D
B
C
A
ED
EA
=
EB
EC
EA • EB = EC • ED
Lengths of sides are
proportional.
Cross Product Property
Proving the Chord Product
Theorem

35. Ex. 1: Finding Segment
Lengths
• Chords ST and PQ
intersect inside the
circle. Find the
value of x.
6
9
3
XR
T
S
Q P
RQ • RP = RS • RT Use Chord Product Theorem
Substitute values.9 • x = 3 • 6
9x = 18
x = 2
Simplify.
Divide each side by 9.

36. Using Segments of Tangents
and Secants
• In the figure shown,
PS is called a
tangent segment
because it is tangent
to the circle at an
end point. Similarly,
PR is a secant
segment and PQ is
the external segment
of PR.
Q
S
P
R

37. Secant – Secant Theorem
• If two secant
segments share the
same endpoint outside
a circle, then the
product of the length
of one secant
segment and the
length of its external
segment equals the
product of the length
of the other secant
segment and the
length of its external
segment.
C
A
D
E
B
EA • EB = EC • ED

38. • If a secant segment
and a tangent
segment share an
endpoint outside a
circle, then the
product of the length
of the secant segment
and the length of its
external segment
equal the square of
the length of the
tangent segment.
(EA)2 = EC • ED
C
D
E
A
Secant – Tangent Theorem

39. Ex. 2: Finding Segment
Lengths
• Find the value of x. x
10
11
9
S
P
T
R
Q
RP • RQ = RS • RT Use Secant-Secant Theorem
Substitute values.9•(11 + 9)=10•(x + 10)
180 = 10x + 100
80 = 10x
Simplify.
Subtract 100 from each side.
8 = x Divide each side by 10.

40. Ex. 3: Estimating the radius of
a circle
• Aquarium Tank.
You are standing
at point C, about 8
feet from a circular
aquarium tank.
The distance from
you to a point of
tangency is about
20 feet. Estimate
the radius of the
tank.

41. (CB)2 = CE • CD Use Secant-Tangent Theorem
Substitute values.
400  16r + 64
336  16r
Simplify.
21  r Divide each side by 16.
(20)2  8 • (2r + 8)
Subtract 64 from each side.
So, the radius of the tank is about 21 feet.
Solution:

42. (BA)2 = BC • BD Use Secant-Tangent Theorem
Substitute values.
25 = x2 + 4x
0 = x2 + 4x - 25
Simplify.
Use Quadratic Formula.
(5)2 = x • (x + 4)
Write in standard form.
Simplify.
Use the positive solution because lengths cannot be
negative. So,
Ex. 4: Finding Segment
Lengths

43. Try This! # 1
 Find the value of x.
x 9
18
12
E
B
D
A
C
9(12) = 18x
108 = 18x
x = 6

44. Try This! # 2
 Find the value of x.
x
10
12
11
H
G
F
E
D
DE  DF = DG DH
11(21) = 12(12 + x)
231 = 144 + 12x
87 = 12x
x = 7.25

45. Try This! # 3
 Find the value of x.
3x5
10
Y
W
X Z
WX2 = XY(XZ)
102 = 5(5 + 3x)
100 = 25 + 15x
75 = 15x
x = 5