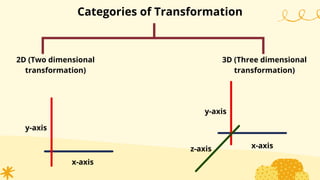
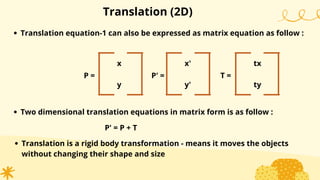
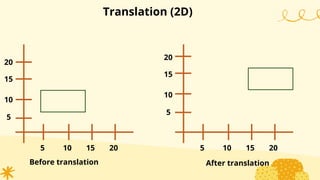
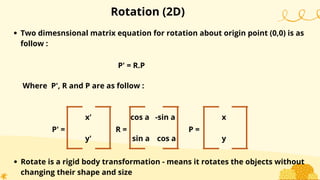
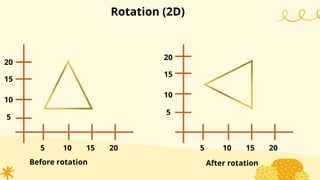
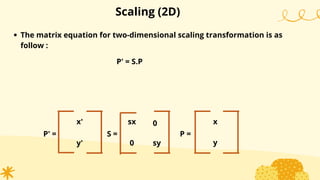
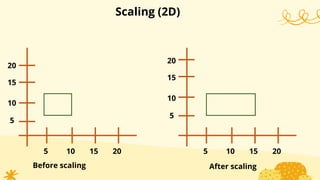
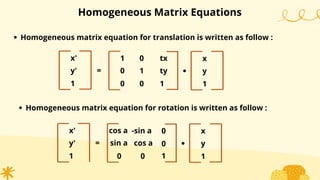
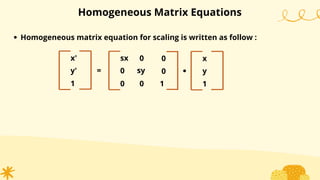
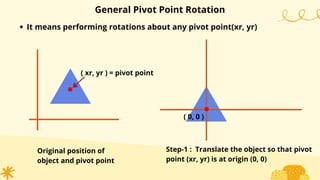
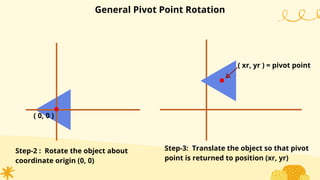
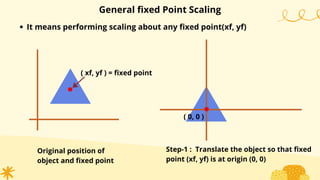
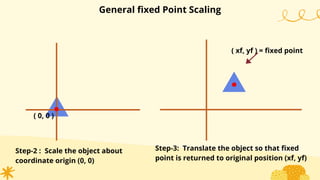
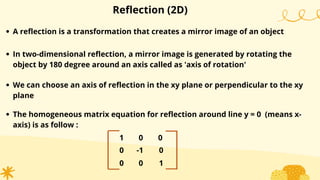
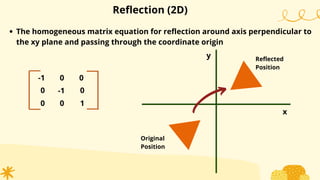
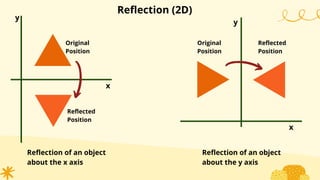
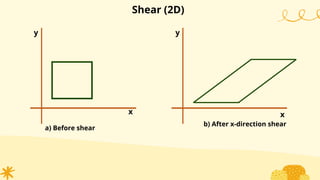
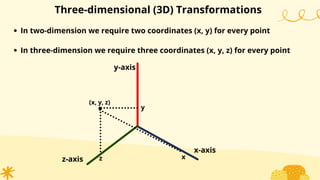
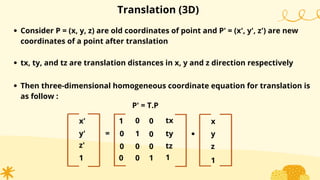
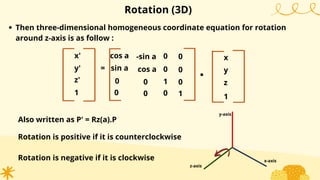
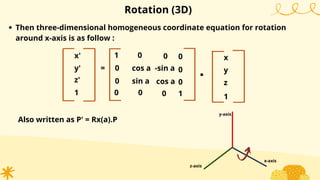
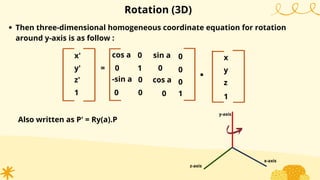
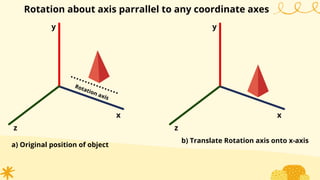
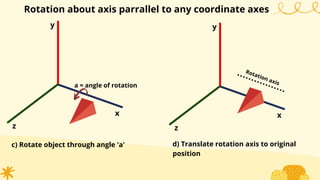
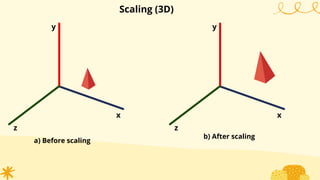
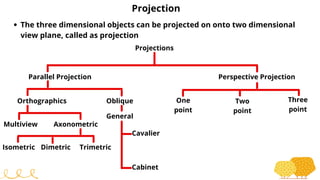
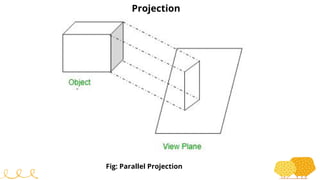
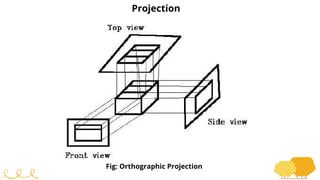
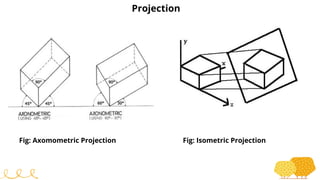
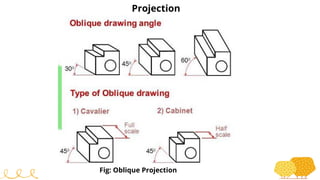
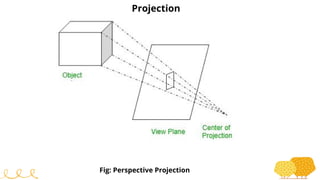
This document provides an overview of transformations in computer graphics. It discusses various 2D and 3D transformations including translation, rotation, scaling, reflection, shear, and their applications. Transformation means changing the orientation, shape, and size of objects or images. Basic 2D transformations discussed are translation, rotation, scaling, reflection, and shear. Homogeneous coordinates and matrix representations are used to combine multiple transformations. The document also discusses general pivot point rotation, fixed point scaling, and 3D transformations.

1. COMPUTER GRAPHICS
by
Amol S. Gaikwad
Lecturer
Government Polytechnic Gadchiroli

2. UNIT-III
OVERVIEW OF
TRANSFORMATIONS

3. Welcome! Are you
excited for a fun
learning session?
Hi!.

4. Unit Outcomes
Perform the given operation in 2D transformation
Perform the given operation in 3D transformation
Solve the given problem based on composite
transformations
Apply the given type of projection on object

5. What is Transformation ?
Transformation means changing orientation, shape and size of
objects or images
We use geometry to achieve transformation
Coordinate descriptions of objects are changed for performing transformation
Basic transformations are as follow :
Translation
Rotation
Scaling

6. What is Transformation ?
Other transformations are as follow :
Reflection
Shear

7. Why Transformation is Needed ?
By using basic shapes we create various types of pictures and graphs
But many applications requires that pictures or images should be altered
and changed
Design applications and layouts are created by arranging the orientation
and sizes of parts
Animations are created by moving objects as per the scene requirements

8. Why Transformation is Needed ?
By using basic shapes we create various types of pictures and graphs
But many applications requires that pictures or images should be altered
and changed
Design applications and layouts are created by arranging the orientation
and sizes of parts
Animations are created by moving objects as per the scene requirements

9. Categories of Transformation
2D (Two dimensional
transformation)
3D (Three dimensional
transformation)
x-axis
y-axis
x-axis
y-axis
z-axis

10. Translation (2D)
In translation we change the location of object from on coordinate position
to other another position along straight line path
let tx and ty are distances , where we want to move our point
Consider (x,y) is the original coordinate position of the point and (x',y') are
new coordinate position of the point, then x' and y' are calculated as follow :
x' = x + tx
y' = y + ty
The pait (tx,ty) are called as translation distance or translation vector or
shift vector
........... equation-1

11. Translation (2D)
Translation equation-1 can also be expressed as matrix equation as follow :
x
y
P =
x'
y'
P' =
tx
ty
T =
Two dimensional translation equations in matrix form is as follow :
P' = P + T
Translation is a rigid body transformation - means it moves the objects
without changing their shape and size

12. Translation (2D)
5 10 15 20 5 10 15 20
5
10
15
20
5
10
15
20
Before translation After translation

13. Rotation (2D)
In two dimesional rotation we reposition the obect along circular path in
the xy-plane
For rotating the object we require angle of rotation 'a' and the position
(xr,yr) of rotation point (pivot point)
Positive angle of rotation means anti-clockwise rotation around rotation
point (pivot point)
Negative angle of rotation means clockwise rotation around rotation point
(pivot point)

14. Rotation (2D)
Two dimesnsional matrix equation for rotation about origin point (0,0) is as
follow :
P' = R.P
Where P', R and P are as follow :
x'
y'
P' =
cos a
sin a
R =
x
y
P =
-sin a
cos a
Rotate is a rigid body transformation - means it rotates the objects without
changing their shape and size

15. Rotation (2D)
5 10 15 20 5 10 15 20
5
10
15
20
5
10
15
20
Before rotation After rotation

16. Scaling (2D)
Scaling transformation alters (changes) the size of an object
Scaling transformation is achieved by multiplying coordinate values (x,y) of
each vertex by scaling factor sx and sy
The transformed coordinates are denoted by (x',y')
x' = x.sx and y' = y.sy
Scaling factors sx scales objects in x direction
Scaling factors sy scales objects in y direction

17. Scaling (2D)
The matrix equation for two-dimensional scaling transformation is as
follow :
P' = S.P
x'
y'
P' =
sx
S =
x
P =
0
sy
0 y

18. Scaling (2D)
If the value of scaling factor sx and sy is less than 1, then the size of the
object decreases
If the value of scaling factor sx and sy is greater than 1, then the size of the
object increases
If the value of scaling factor sx = sy = 1, then the size of the object remains
unchanged
If the value of scaling factor sx = sy, then uniform scaling is achieved which
maintains relative proportion of the object
If the value of scaling factor sx is not equal to sy then differential scaling is
achieved

19. Scaling (2D)
5 10 15 20 5 10 15 20
5
10
15
20
5
10
15
20
Before scaling After scaling

20. Scaling (2D)
If the value of scaling factor sx and sy is less than 1, then the object moves
closer to the coordinate origin (0,0)
If the value of scaling factor sx and sy is greater than 1, then the object
moves away from the coordinate origin (0,0)

21. Homogeneous Coordinates and Matrix Representations
In many computer graphics applications we require to perform
translations, rotations and scalings transformations sequencially
With the help of homogeneous coordinates, we can combine various
transformations so that final coordinates are obtained directly from the
initial (starting) coordinates
It eliminates the calculations of intermediate coordinate values
By expanding the 2x2 matrix into 3x3 matrix, we combine the
multiplicative and translational terms for 2D geometric transformations
into single matrix

22. Homogeneous Coordinates and Matrix Representations
Homogeneous coordinates are used to express any 2D transformation as a
matrix multiplication
We represent each cartesian coordinate position (x,y) with homogeneous
coordinate triple (xh, yh, h)
where we take value of h = 1
Each two-dimensional (2D) position is then represented with homogenous
coordinates (x, y, 1)

23. Homogeneous Matrix Equations
Homogeneous matrix equation for translation is written as follow :
x'
y'
1
=
1
0
0
0
1
0
tx
ty
1
.
x
y
1
Homogeneous matrix equation for rotation is written as follow :
x'
y'
1
=
cos a
0
-sin a
0
0
1
.
x
y
1
sin a cos a 0

24. Homogeneous Matrix Equations
Homogeneous matrix equation for scaling is written as follow :
x'
y'
1
=
sx
0
0
0
sy
0
0
1
.
x
y
1
0

25. Composite Transformations
Composite transformation means performing various types of
transformations in sequence
Forming products of transformation matrices is often referred to as a
concatenation or composition of matrices
For column matrix representation of coordinate positions, we form
composite transformations by multiplying matrices in order from right to
left

26. Composite Transformations
Homogeneous matrix equation for two successive translations is as follow :
1
0
0
0
1
0
tx1
ty1
1
.
Homogeneous matrix equation for two successive scalings are as follow :
1
0
0
0
1
0
tx2
ty2
1
1
0
0
0
1
0
tx1 + tx2
ty1 + ty2
1
=
sx1
0
0
0
sy1
0
0
0
1
.
sx2
0
0
0
sy2
0
0
0
1
sx1.sx2
0
0
0
sy1.sy2
0
0
0
1
=

27. General Pivot Point Rotation
It means performing rotations about any pivot point(xr, yr)
.
.
( xr, yr ) = pivot point
( 0, 0 )
Original position of
object and pivot point
Step-1 : Translate the object so that pivot
point (xr, yr) is at origin (0, 0)

28. General Pivot Point Rotation
( xr, yr ) = pivot point
.
( 0, 0 )
.
Step-2 : Rotate the object about
coordinate origin (0, 0)
Step-3: Translate the object so that pivot
point is returned to position (xr, yr)

29. General fixed Point Scaling
It means performing scaling about any fixed point(xf, yf)
.
.
( xf, yf ) = fixed point
( 0, 0 )
Original position of
object and fixed point
Step-1 : Translate the object so that fixed
point (xf, yf) is at origin (0, 0)

30. ( xf, yf ) = fixed point
( 0, 0 )
.
Step-2 : Scale the object about
coordinate origin (0, 0)
Step-3: Translate the object so that fixed
point is returned to original position (xf, yf)
General fixed Point Scaling
.

31. Other Transformations
Translation, rotation and scaling are called as basic transformations
Most computer graphics packages provide these basic transformations of
translation, rotation and scaling
Some computer graphics packages also provide additional
transformations they are as follow :
Reflection
Shear

32. Reflection (2D)
A reflection is a transformation that creates a mirror image of an object
In two-dimensional reflection, a mirror image is generated by rotating the
object by 180 degree around an axis called as 'axis of rotation'
We can choose an axis of reflection in the xy plane or perpendicular to the xy
plane
The homogeneous matrix equation for reflection around line y = 0 (means x-
axis) is as follow :
1
0
0
0
-1
0 1
0
0

33. Reflection (2D)
Reflection around x-axis (means y = 0), keeps the x-values same but reverses
the y values
-1
0
0
0
1
0 1
0
0
It is same as rotating the object by 180 degree in three-dimensional space
around x-axis
The homogeneous matrix equation for reflection around line x= 0 (means y-
axis) is as follow :

34. Reflection (2D)
-1
0
0
0
-1
0 1
0
0
The homogeneous matrix equation for reflection around axis perpendicular to
the xy plane and passing through the coordinate origin
Original
Position
Reflected
Position
x
y

35. Reflection (2D)
Reflection of an object
about the x axis
Original
Position
Reflected
Position
x
y
Original
Position
Reflected
Position
Reflection of an object
about the y axis
x
y

36. Shear (2D)
Shear is a transformation that distorts (changes) the shape of object
It transforms the object such that the object appears to be composed of
internal layers and the layers slide over each other
Two common shearing transformations are those that shift coordinate x
values and those that shift y values
Two-dimensional homogeneous matrix equation for x-direction shear is as
follow :
1
0
0
shx
1
0 1
0
0
Where x' = x + shx.y
y' = y

37. Shear (2D)
a) Before shear
b) After x-direction shear
x
y
x
y

38. Three-dimensional (3D) Transformations
In two-dimension we require two coordinates (x, y) for every point
In three-dimension we require three coordinates (x, y, z) for every point
x-axis
y-axis
z-axis
.
(x, y, z)
z
y
x

39. Translation (3D)
Consider P = (x, y, z) are old coordinates of point and P' = (x', y', z') are new
coordinates of a point after translation
tx, ty, and tz are translation distances in x, y and z direction respectively
Then three-dimensional homogeneous coordinate equation for translation is
as follow :
P' = T.P
x'
y'
1
=
1
0
0
0
1
0
0
1
.
x
y
1
0
0
z'
0
0
ty
1
tx
tz z

40. Then three-dimensional homogeneous coordinate equation for rotation
around z-axis is as follow :
=
Rotation (3D)
Also written as P' = Rz(a).P
x'
y'
1
cos a
sin a
0
-sin a
cos a
0
0
0
.
x
y
1
0
0
z'
0
1
0
1
0
0 z
x-axis
y-axis
z-axis
Rotation is positive if it is counterclockwise
Rotation is negative if it is clockwise

41. Rotation (3D)
Then three-dimensional homogeneous coordinate equation for rotation
around x-axis is as follow :
Also written as P' = Rx(a).P
x'
y'
1
= cos a
sin a
0
-sin a
cos a
0
0
0
.
x
y
1
0
0
z'
0
1
0
1
0
0 z
x-axis
y-axis
z-axis

42. Rotation (3D)
Then three-dimensional homogeneous coordinate equation for rotation
around y-axis is as follow :
Also written as P' = Ry(a).P
x'
y'
1
=
cos a sin a
0
-sin a cos a
0
0
0
.
x
y
1
0
0
z'
0
1 0
1
0
0 z
x-axis
y-axis
z-axis

43. Rotation about axis parrallel to any coordinate axes
x
y
z
a) Original position of object
Rotation axis
x
y
z
b) Translate Rotation axis onto x-axis

44. Rotation about axis parrallel to any coordinate axes
c) Rotate object through angle 'a'
x
y
z
a = angle of rotation
x
y
z
d) Translate rotation axis to original
position
Rotation axis

45. Scaling (3D)
Consider P = (x, y, z) are old coordinates of point and P' = (x', y', z') are new
coordinates of a point after scaling
Sx, Sy and Sz are values of scaling parameters
Where x' = x.Sx , y' = y.Sy and z' = z.Sz
Then three-dimensional homogeneous coordinate equation for rotation
around y-axis is as follow :
x'
y'
1
=
Sx
0
0
0
Sy
0
0
0
.
x
y
1
0
0
z'
0
Sz z
0
1
0
0

46. Scaling (3D)
x
y
z
a) Before scaling
x
y
z
b) After scaling

47. Scaling (3D)
x
y
z
a) Before scaling
x
y
z
b) After scaling

48. Projection
The three dimensional objects can be projected on onto two dimensional
view plane, called as projection
Projections
Parallel Projection Perspective Projection
Orthographics Oblique
Multiview Axonometric
Dimetric
Isometric Trimetric
General
Cavalier
Cabinet
One
point
Two
point
Three
point

49. Projection
Parallel Projection :
In parallel projection the lines of projection are parallel to each other
Coordinate position are transformed to the view plane in along parallel
lines
It maintains the relative proportions of objects
It is used for scale drawings of three-dimensional objects
It gives us accurate view of various sides of an object
But it doesn't give us realistic representation of appearance of three-
dimensional objects

50. Projection
Fig: Parallel Projection

51. Projection
Orthographic Projection :
It is a type of parallel projection
In this projection, the projection lines are perpendicular to the view plane
Orthographic projections are used to produce the front, side, and top
views of an object
Front, side, and rear orthographic projections of an object are called as
elevations
Top orthographic projection is called as plan view
Orthographic projections are commonly used by engineering and
architectural drawings

52. Projection
Fig: Orthographic Projection

53. Projection
Axonometric Projection :
It is a type of orthographic projection
This projection displays more than one face of an object
In axonometric projection scaling factor may be different for three axes -
x, y and z
Isometric Projection :
It is a type of Axonometric projection
In this projection, the projection plane is kept in such a position such
that it intersects each coordinates axis (x, y and z axis) at same distance
from the origin

54. Projection
Fig: Axomometric Projection Fig: Isometric Projection

55. Projection
Oblique Projection :
It is a type of parallel projection
In this projection, the projection lines are not perpendicular to the view
plane
The two types of oblique projections are cavalier projection and cabinet
projection

56. Projection
Fig: Oblique Projection

57. Projection
Perspective Projection :
In perspective projection the lines of projections are not parallel to each
other
Object positions are transferred to the plane along lines that meet at a
point called as projection reference point or center of projection
The projected view of object is calculated from the intersection of the
projected lines with the view plane
It creates realistic view of an object
It does not preserve relative proportion of the object

58. Projection
Types of Perspective Projection :
One-point
In this any one principal axes intersect with the projection plane
Projection plane is perpendicular to any one principal axis
Two-point
In this two principal axes intersect with the projection plane
Three-point
In this all the three principal axes (x, y, z) intersect with the projection
plane

59. Projection
Fig: Perspective Projection

60. Activity Time
Problems worksheet
Programming
Assignment

61. Supplemental Video
https://nptel.ac.in/courses/1
06/102/106102065/

62. Additional Resources
https://www.tutorialspoint.com/computer_graphics
https://nptel.ac.in/courses/106/102/106102065
Computer Graphics - Donald Hearn, Baker M Pauline, Pearson Education

63. Summary of Class
2D Transformations
Lesson Recap 1
3D Transformations
Lesson Recap 2
Composite Transformations
Lesson Recap 3
Types of projections
Lesson Recap 4

64. Thank you for attending!