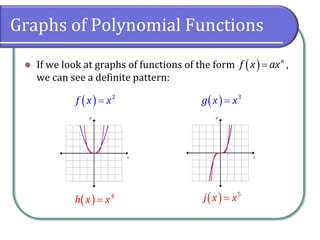
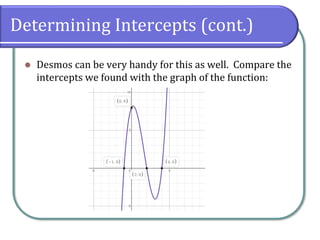
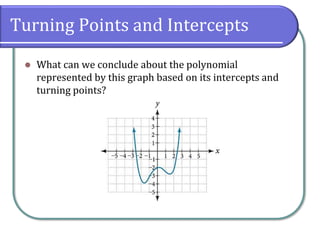
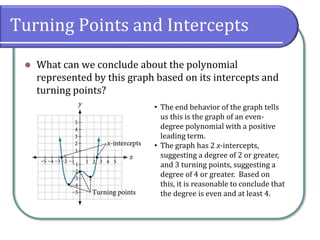
This document explains power and polynomial functions, covering their definitions, forms, and characteristics, including degree and leading coefficients. It also discusses end behavior, turning points, intercepts, and how to determine these features through graphs and examples. Finally, it provides exercises for practice related to these concepts.

1. 5.2 Power Functions &
Polynomial Functions
Chapter 5 Polynomial and Rational Functions

2. Concepts and Objectives
⚫ Objectives for the section are
⚫ Identify power functions.
⚫ Identify end behavior of power functions.
⚫ Identify polynomial functions.
⚫ Identify the degree and leading coefficient of
polynomial functions.

3. Power Functions
⚫ A power function is a function with a single term that is
the product of a real number (the coefficient) and a
variable raised to a fixed real number.
⚫ It can be represented in the form
where k and p are real numbers.
( )= ,
p
f x kx

4. Power Functions (cont.)
⚫ Examples of power functions:
⚫
⚫
⚫
⚫ Non-examples of power functions:
⚫
⚫
( ) 3
f x x
=
( ) 2
f x x
= ( )
1
2
x
( ) 2
1
f x
x
= ( )
2
x−
( ) 2
4 1
f x x
= −
( )
5
2
2 1
3 4
x
f x
x
−
=
+

5. Polynomial Functions
⚫ A polynomial function consists of either zero or the sum
of a finite number of non-zero terms, each of which is a
product of a number (the coefficient) and a variable
raised to a non-negative integer (≥1) power
⚫ Let n be a non-negative integer. A polynomial function is
a function that can be written in the form
⚫ This is called the general form of a polynomial function.
Each ai is a coefficient and can be any real number, but
an ≠ 0.
( ) 2
2 1 0
n
n
f x a x a x a x a
= + + + +

6. Polynomial Functions (cont.)
⚫ Polynomial functions are different from power functions
in that
⚫ they can consist of multiple terms combined by
addition or subtraction
⚫ their exponents must be non-negative integers

7. The Degree and Leading Term
⚫ The degree of a polynomial (or power) function is the
highest power of the variable that occurs in the
polynomial.
⚫ The leading term is the term containing the highest
power of the variable.
⚫ The leading coefficient is the coefficient of the leading
term.
⚫ The leading term does not have to be the first term in
the polynomial.

8. Identifying the Degree and Leading
Coefficient
Examples: Identify the degree and the leading coefficient
of the following polynomial functions.
⚫ f
⚫
⚫
( ) 5 3
6 2 7
f t t t t
= − +
( ) 2 3
3 2 4
g x x x
= + −
( ) 3
6 2
h p p p
= − −

9. Identifying the Degree and Leading
Coefficient
Examples: Identify the degree and the leading coefficient
of the following polynomial functions.
⚫ f
Degree: 5 Leading coefficient: 6
⚫
Degree: 3 Leading coefficient: ‒4
⚫
Degree: 3 Leading coefficient: ‒1
( ) 5 3
6 2 7
f t t t t
= − +
( ) 2 3
3 2 4
g x x x
= + −
( ) 3
6 2
h p p p
= − −

10. Graphs of Polynomial Functions
⚫ If we look at graphs of functions of the form ,
we can see a definite pattern:
( )= n
f x ax
( )= 2
f x x ( )= 3
g x x
( )= 4
h x x ( )= 5
j x x

11. End Behavior
⚫ The end behavior of a polynomial graph is determined by
the leading term (also called the dominating term).
⚫ For example, has the same end
behavior as once you zoom out far enough.
( )= − +
3
2 8 9
f x x x
( )= 3
2
f x x

12. End Behavior
⚫ Example: Use symbols for end behavior to describe the
end behavior of the graph of each function.
1.
2.
3.
( )= − + + −
4 2
2 8
f x x x x
( )= + − +
3 2
2 3 5
g x x x x
( )= − + +
5 3
2 1
h x x x

13. End Behavior
⚫ Example: Use symbols for end behavior to describe the
end behavior of the graph of each function.
1.
2.
3.
( )= − + + −
4 2
2 8
f x x x x even function
opens downward
( )= + − +
3 2
2 3 5
g x x x x odd function
increases
( )= − + +
5 3
2 1
h x x x odd function
decreases

14. Turning Points and Intercepts
⚫ The point where a graph changes direction (“bounces”
or “wiggles”) is called a turning point of the function.
⚫ The y-intercept is the point at which the function has an
input value of zero.
⚫ The x-intercepts are the points at which the output value
is zero.

15. Determining Intercepts
⚫ To find the y-intercept, substitute 0 for every x.
⚫ To find the x-intercept(s), set the polynomial equal to
zero and solve for x.
Example: Find the intercepts of
⚫ y-intercept:
⚫ x-intercepts:
( ) ( )( )( )
2 1 4
f x x x x
= − + −
( ) ( )( )( )
( )( )( )
0 0 2 0 1 0 4
2 1 4 8
f = − + −
= − − =
( )( )( )
0 2 1 4
x x x
= − + −
2 0
2
x
x
− =
=
or
1 0
1
x
x
+ =
= −
or
4 0
4
x
x
− =
=

16. Determining Intercepts (cont.)
⚫ Desmos can be very handy for this as well. Compare the
intercepts we found with the graph of the function:

17. Turning Points and Intercepts
⚫ A polynomial function of degree n will have at most
n x-intercepts and n – 1 turning points, with at least one
turning point between each pair of adjacent zeros.
(Because it is a function, there is only one y-intercept.)
⚫ Example: Without graphing the function, determine the
local behavior of the function by finding the maximum
number of x-intercepts and turning points for
⚫ The polynomial has a degree of 10, so there are at
most 10 x-intercepts and at most 9 turning points.
( ) 10 7 4 3
3 4 2
f x x x x x
= − + − +

18. Turning Points and Intercepts
⚫ What can we conclude about the polynomial
represented by this graph based on its intercepts and
turning points?

19. Turning Points and Intercepts
⚫ What can we conclude about the polynomial
represented by this graph based on its intercepts and
turning points?
• The end behavior of the graph tells
us this is the graph of an even-
degree polynomial with a positive
leading term.
• The graph has 2 x-intercepts,
suggesting a degree of 2 or greater,
and 3 turning points, suggesting a
degree of 4 or greater. Based on
this, it is reasonable to conclude that
the degree is even and at least 4.

20. Putting It All Together
⚫ Use the information below about the graph of a
polynomial function to determine the function. Assume
the leading coefficient is 1 or ‒1.
The y-intercept is (0, ‒4). The x-intercepts are (‒2, 0),
(2, 0). Degree is 2. End behavior:

21. Putting It All Together
⚫ Use the information below about the graph of a
polynomial function to determine the function. Assume
the leading coefficient is 1 or ‒1.
The y-intercept is (0, ‒4). The x-intercepts are (‒2, 0),
(2, 0). Degree is 2. End behavior:
( ) ( )( )
2 2
f x x x
= + −

22. Classwork
⚫ College Algebra 2e
⚫ 5.2: 12-24 (even); 5.1: 26-32, 40-44 (even); 4.3: 32-
42 (even)
⚫ 5.2 Classwork Check
⚫ Quiz 5.1