Solo Hermelin, profile picture
Uploaded bySolo Hermelin
PPT, PDF2,345 views

Conic sections

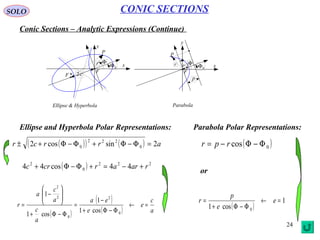
The document provides a comprehensive overview of conic sections, including definitions and properties of circles, ellipses, parabolas, and hyperbolas formed by intersecting a right circular cone with a plane. It explains how the angle of intersection affects the type of conic section produced and includes mathematical expressions and diagrams for better understanding. The historical context of conic sections is also mentioned, attributing their discovery to the Greek mathematician Menachmus.

Embed presentation

Downloaded 68 times
1 CONIC SECTIONS SOLO HERMELIN http://www.solohermelin.com
2 SOLO Table of Contents 2. Circle 3. Ellipse 4. Parabola 5. Hyperbola 6. Conic sections – Analytic Expressions 7. Conic sections – General Description CONIC SECTIONS 1. Conic Sections - Introduction 8. References
3 SOLO A right circular cone is a cone obtained by generators (straight lines) passing through a circle, and the apex C that is situated on the normal to the circle plane and passing trough the center of the circle. β is the angle between the cone axis and the generators. CONIC SECTIONS Cutting Plane generating a "hyperbola" Right Circular Cone Cone Apex Conical Section C Cone Axis Cutting Plane generating a "parabola" Cutting Plane generating a "ellipse" Cutting Plane generating a "circle" Cutting Plane generating two "lines" α β       −= β π α 2       −< β π α 2       −> β π α 2 ( )0=α                   −> −= −< lines line po 2 2 1 2 int 2 β π α β π α β π α P F F * Cutting Plane (Hyperbola ) Right Circular Cone Hyperbola 2 Branches C β α Ellipse Parabola Cutting Plane (Ellipse) Cutting Plane (Circle) Cutting Plane (Parabola) By cutting the right circular conic by a plane we obtain different conic sections, as a function of the inclination angle α of the plane relative to the base of the conic section and the angle β between the generators and the base. The discovery of the Conical Sections is attributed to the greek Menachmus who lived around 350 B.C.. 1. Conic Sections - Introduction
4 SOLO The conical sections are: CONIC SECTIONS 1. Circle if the cutting plane is normal to the cone axis (α=0) and is above or bellow the apex. 2. Ellipse if the cutting plane is inclined to the basis at an angle that falls short of the angle between generators to the base (α<π/2-β) (in greek word elleipsis means falls, short or leaves out. 3. Hyperbola if the cutting plane is inclined to the basis at an angle that exceeds of the angle between generators to the base (α>π/2-β)(in greek word hyperbole means excess. 4. Parabola if the cutting plane is parallel to a generator of the right circular cone (α=π/2-β) (in greek word parabole is the origin of the words parabola and parallel. 5. A point- apex (α<π/2-β), one straight line (α=π/2-β), two straight lines (α>π/2-β), if the cutting plane passes through the apex and intersects the cone basis.
5 SOLO CONIC SECTIONS Circle if the cutting plane is normal to the cone axis (α=0) and is above or bellow the apex. 2. Circle
6 SOLO CONIC SECTIONS 3 Ellipse (α < π/2-β) To find the properties of the ellipse let introduce two spheres, with centers on the cone axis, inside the right circular cone, one the above the cutting plane and one bellow. The sphere are tangent to the right cone surfaces, along one circle each (C1 for sphere 1 and C2 for sphere 2, with centers on cone axis and parallel to cone base), and tangent to cutting plane at the points F* (sphere 1) and F (sphere 2). The center of the spheres are in the plane perpendicular to the cutting plane. They contain the cone axis, and are the intersection of this axis with the line bisecting one of the angles generated between the cone generators and intersection of perpendicular and cutting planes.
7 SOLO CONIC SECTIONS Ellipse (α < π/2-β) (Continue – 1) Let draw the cone generator CP (where C is the cone apex and P is any point on the Ellipse). Since PF* is tangent to sphere 1 and PF is tangent to sphere 2, and since the tangent distances to a sphere from the same points are equal, we have: ** PQPF = PQPF = Therefore QQPQPQPFPF *** =+=+ Since Q* is on circle C1 and Q on circle C2 and on the same generator the distance Q*Q is independent on P. Ellipse (Definition 1) Ellipse is a planar curve, such that the sum of distances, from any point on the curve, to two fixed points (foci) in the plane is constant.
8 SOLO CONIC SECTIONS Ellipse (α < π/2-β) (Continue – 2) One other definition is obtained by the following construction: The intersection between cutting plane and the plane containing circle C1 is called directrix 1. The intersection between cutting plane and the plane containing circle C2 is called directrix 2. The point M* on directrix 1 is on the normal from P on directrix 1 (PM* ┴ directrix 1). The point M on directrix 2 is on the normal from P on directrix 2 (PM ┴ directrix 2). The distance from the point P to the plane containing circle C1 (that contains both Q* and M*) is given by The distance from the point P to the plane containing circle C2 (that contains both Q and M) is given by ββα cos*cos*sin* ** PFPQPM PFPQ = == ββα coscossin PFPQPM PFPQ = == From those equations we obtain: Since for an ellipse α<π/2-β → sinα<sin(π/2-β) we have: β α cos sin * * == PM PF PM PF 1 cos sin : <= β α e e - eccentricity
9 SOLO CONIC SECTIONS Ellipse (α < π/2-β) (Continue – 3) We obtained: 1 cos sin * * <=== e PM PF PM PF β α P F Q* Q Cutting Plane Right Circular Cone Sphere2 Tangent to Cone at Q & Cutting Plane at F Sphere1 Tangent to Cone at Q* & Cutting Plane at F* Cone Appex Circle C1 on the Cone & Sphere1 Circle C2 on the Cone & Sphere2 R1 R2 C M* M Directrix 2 Directrix 1 α β F* PQPF = ** PQPF = constQQ PQPQ PFPF = =+ =+ * * * β β α cos cos sin PF PQ PM = = β β α cos* cos* sin* PF PQ PM = = 1: cos sin * * <=== e PM PF PM PF β α Ellipse (Definition 2) Ellipse is a planar curve, such that the ratio of distances, from any point on the curve, to a fixed point F* (focus 1) and to the line directrix1 and ratio of distances to a second fixed point F and the second line directrix 2 (parallel to directrix1) are constant and equal to e < 1. The focci F* and F are between the two directrices, where F* is closer to directrix 1 and F to directrix 2. The proof given here was supplied in 1822 by the Belgian mathematician Germinal P. Dandelin (1794-1847)
10 SOLO CONIC SECTIONS 4. Parabola (α = π/2-β) To find the properties of the parabola let introduce a sphere, with center on the cone axis, inside the right circular cone, above the cutting plane. The sphere is tangent to the right cone surfaces, along one circle C with center on cone axis and parallel to cone base, and tangent to cutting plane at point F. Let draw the cone generator CP (where C is the cone apex and P is any point on the Parabola). CP is tangent to the sphere at point Q (on circle C). Since PF is tangent to the sphere, and all tangents from the same point are equal PF = PQ. Let perform the following construction:The intersection between cutting plane and the plane containing circle C is called directrix. The point M on directrix is on the normal from P on directrix (PM ┴ directrix). The distance from the point P to the plane containing circle C (that contains both Q and M) is given by ββα coscossin PFPQPM PFPQ = ==
11 SOLO CONIC SECTIONS Parabola (α = π/2-β) (Continue – 1) P F Q Cutting Plane Right Circular Cone SphereTangent to Cone at Q* & Cuting Plane at F* Cone Apex Plane Containin g the Circle Tangent to Cone & Sphere Circle Tangent to Cone & Sphere β βπα −= 2/ M Directrix PQPF = β β α cos cos sin PF PQ PM = = e PM PF === :1 cos sin β α The distance from the point P to the plane containing circle C (that contains both Q and M) is given by ββα coscossin PFPQPM PFPQ = == β α cos sin = PM PF From those equations we obtain: Since for a parabola α = π/2-β → sinα = sin(π/2-β)=cos β we have: e - eccentricity 1 cos sin : == β α e e - eccentricity Parabola (Definition) Parabola is a planar curve, such that the distances, from any point on the curve, to a fixed point (focus) and to the line directrix are equal.
12 SOLO CONIC SECTIONS 5. Hyperbola (α > π/2-β) To find the properties of the hyperbola let introduce two spheres, with centers on the cone axis, inside the right circular cone, one the above the apex and one bellow. The sphere are tangent to the right cone surfaces, along one circle each (C1 for sphere 1 and C2 for sphere 2, with centers on cone axis and parallel to cone base), and tangent to cutting plane at the points F* (sphere 1) and F (sphere 2). The center of the spheres are in the plane perpendicular to the cutting plane. They contain the cone axis, and are the intersection of this axis with the line bisecting one of the angles generated between the cone generators and intersection of perpendicular and cutting planes.
13 SOLO CONIC SECTIONS Hyperbola (α > π/2-β) (Continue – 1) Let draw the cone generator CP (where C is the cone apex and P is any point on the Hyperbola). Since PF* is tangent to sphere 1 and PF is tangent to sphere 2, and since the tangent distances to a sphere from the same points are equal, we have: ** PQPF = PQPF = Therefore *** QCQPQPQPFPF =−=− Since Q* is on circle C1 and Q on circle C2 and on the same generator the distance Q*Q is independent on P. P F F* Q Cutting Plane Right Circular Cone Sphere1 Tangent to Cone & Cuting Plane at F* Cone Apex Circle on the Sphere2 & Cone Sphere2 Tangent to Cone & Cuting Plane at F Circle on the Sphere1 & Cone Conical Section Conical Section C Q* Cone Axis Hyperbola (Definition 1) Hyperbola is a planar curve, such that the difference of distances, from any point on the curve, to two fixed points (foci) in the plane is constant. Hyperbola has two branches.
14 SOLO CONIC SECTIONS Hyperbola (α > π/2-β) (Continue – 2) One other definition is obtained by the following construction: The intersection between cutting plane and the plane containing circle C1 is called directrix 1. The intersection between cutting plane and the plane containing circle C2 is called directrix 2. The point M* on directrix 1 is on the normal from P on directrix 1 (PM* ┴ directrix 1). The point M on directrix 2 is on the normal from P on directrix 2 (PM ┴ directrix 2). The distance from the point P to the plane containing circle C1 (that contains both Q* and M*) is given by The distance from the point P to the plane containing circle C2 (that contains both Q and M) is given by ββα cos*cos*sin* ** PFPQPM PFPQ = == ββα coscossin PFPQPM PFPQ = == From those equations we obtain: Since for an ellipse α>π/2-β → sinα>sin(π/2-β) we have: β α cos sin * * == PM PF PM PF 1 cos sin : >= β α e e - eccentricity P F F* Q Cutting Plane Right Circular Cone Sphere1 Tangent to Cone & Cuting Plane at F* Cone Apex Sphere2 Tangent to Cone & Cuting Plane at F Circle C1 on the Sphere1 & Cone Conical Section Conical Section Q* CCircle C2 on the Sphere2 & Cone PQPF = ** PQPF = constQCQ PQPQ PFPF = =− =− * * * β β α cos cos sin PF PQ PM = = β β α cos* cos* sin* PF PQ PM = = ( )βπα −> 2/ β Directrix1 Directrix2M M* α 1: cos sin * * >=== e PM PF PM PF β α
15 SOLO CONIC SECTIONS Hyperbola (α < π/2-β) (Continue – 3) We obtained: 1 cos sin * * >=== e PM PF PM PF β α Hyperbola (Definition 2) Hyperbola is a planar curve, such that the ratio of distances, from any point on the curve, to a fixed point F* (focus 1) and to the line directrix1 and ratio of distances to a second fixed point F and the second line directrix 2 (parallel to directrix1) are constant and equal to e > 1. The focci F* and F are between the two directrices, where F* is closer to directrix 1 and F to directrix 2. P F F* Q Cutting Plane Right Circular Cone Sphere1 Tangent to Cone & Cuting Plane at F* Cone Apex Sphere2 Tangent to Cone & Cuting Plane at F Circle C1 on the Sphere1 & Cone Conical Section Conical Section Q* CCircle C2 on the Sphere2 & Cone PQPF = ** PQPF = constQCQ PQPQ PFPF = =− =− * * * β β α cos cos sin PF PQ PM = = β β α cos* cos* sin* PF PQ PM = = ( )βπα −> 2/ β Directrix1 Directrix2M M* α 1: cos sin * * >=== e PM PF PM PF β α
16 SOLO CONIC SECTIONS 6. Conic Sections – Analytic Expressions ( ) ( ) aycxycx 22222 =++±+− ( ) ( ) 2222 2 ycxaycx +−−=++± ( ) ( ) ( ) 2222222 44 ycxaycxaycx +−−+−+=++ ( ) 22 ycxa a xc +−−=− 2222 2 22 22 ycxcxaxc a cx ++−=+− 222 2 22 2 cay a ca x −=+ −122 2 2 2 = − + ca y a x cacab b y a x >←−=←=+ 222 2 2 2 2 1 caacb b y a x <←−=←=− 222 2 2 2 2 1 012 2 2 2 =←=+ c a y a x ellipse hyperbola circle Start with ellipse and hyperbola definitions:
17 SOLO CONIC SECTIONS Conic Sections – Analytic Expressions (Continue) Ellipse and Hyperbola Polar Representations: Φ 0Φ P F *F x y r c2 Φ 0Φ P F x y r p 2/p Ellipse & Hyperbola Parabola Parabola Polar Representations: ( )( ) ( ) arrcr 2sincos2 0 222 0 =Φ−Φ+Φ−Φ+± ( ) 222 0 2 44cos44 rararcrc +−=+Φ−Φ+ ( ) ( ) ( ) a c e e ea a c a c a r =← Φ−Φ+ − = Φ−Φ+       − = 0 2 0 2 2 cos1 1 cos1 1 ( )0cos Φ−Φ−= rpr ( ) 1 cos1 0 =← Φ−Φ+ = e e p r or
18 SOLO CONIC SECTIONS 7. Conic Sections – General Description Let perform a rotation of coordinates: 022 =+++++ FYEXDYCXYBXA ϕϕ ϕϕ cossin sincos yxY yxX +−= += ( ) 0cossinsincos sincoscossincossin cossin2cossin cossin2sincos 2222 2222 2222 =++−++ −++− −++ ++ FEyxEyDxD yxByBxB yxCyCxC yxAyAxA ϕϕϕϕ ϕϕϕϕϕϕ ϕϕϕϕ ϕϕϕϕ Choose φ such that the coefficient of xy is zero: ( ) ( ) 0sincoscossin2 22 =−−− ϕϕϕϕ BAC ( ) AC B − =02tan ϕ
19 SOLO CONIC SECTIONS Conic Sections – General Description (Continue – 1) 0cossinsincos cossincossin cossin sincos 0000 00 2 00 2 ) 22 0 22 0 22 0 22 =++−++ +− ++ + FEyxEyDxD yBxB yCxC yAxA ϕϕϕϕ ϕϕϕϕ ϕϕ ϕϕ ( ) ( ) ( ) ( ) 0cossinsincos cossincossincossinsincos 0000 2 00) 2 0 22 000 2 0 2 =+++−+ +++−+ FyEDxED yBCAxBCA ϕϕϕϕ ϕϕϕϕϕϕϕϕ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 cossincossin2 cossin cossinsincos2 sincos cossincossin2 cossin cossincossin cossinsincos2 sincos cossinsincos 2 00) 2 0 2 00 2 000 2 0 2 00 2 00) 2 0 2 00 00) 2 0 2 2 000 2 0 2 00 000 2 0 2 1 1 =+         ++ + −        −+ − −         ++ + ++++         −+ − +−+ F BCA ED BCA ED BCA ED yBCA BCA ED xBCA C A ϕϕϕϕ ϕϕ ϕϕϕϕ ϕϕ ϕϕϕϕ ϕϕ ϕϕϕϕ ϕϕϕϕ ϕϕ ϕϕϕϕ       We obtain or or
20 SOLO CONIC SECTIONS Conic Sections – General Description (Continue – 2) Let define ( )000 2 0 2 1 cossinsincos: ϕϕϕϕ BCAA −+= ( )00) 2 0 2 1 cossincossin: ϕϕϕϕ BCAC ++= 001 001 cossin: sincos: ϕϕ ϕϕ EDE EDD += −= We can see that CACA +=+ 11 1. If A1 ≠ 0 & C1 ≠ 0. We define ( ) ( ) ( ) ( ) 2 00) 2 0 2 00 2 000 2 0 2 00 1 cossincossin2 cossin cossinsincos2 sincos :         ++ + −      −+ − −= ϕϕϕϕ ϕϕ ϕϕϕϕ ϕϕ BCA ED BCA ED FF If A1, C1, F1 ≠ 0 do not have the same algebraic sign, than the equation is an equation of an ellipse, circle or hyperbola 1 1 1 2 A D xx += 1 1 1 2C E yy += The equation becomes: 01 2 11 2 11 =++ FyCxA If sign A1 = sign C1 ≠ sign F1 & A1 = C1 → circle If sign A1 = sign C1 ≠ sign F1 & A1 ≠ C1 → ellipse If sign A1 ≠ sign C1 → hyperbola
21 SOLO CONIC SECTIONS Conic Sections – General Description (Continue – 3) 2. If A1 = 0 , C1 ≠ 0 & D1 ≠ 0. We define 1 2 1 1 1 2 : D C E F xx       − += 1 1 1 2 : C E yy += Parabola011 2 11 =+ xDyCThe equation becomes: Parabola011 2 11 =+ yExAThe equation becomes: 3. If A1 ≠ 0 , C1 = 0 & E1 ≠ 0. We define 1 1 1 2 : A D xx += 1 1 1 1 2 : E A D F yy       − +=
22 SOLO CONIC SECTIONS Conic Sections – General Description (Continue – 4) The equation can be rewritten as022 =+++++ FYEXDYCXYBXA [ ] [ ] 0 1 2 1 2 1 2 1 2 1 2 1 2 1 1 2 1 2 1 2 1 2 1 2 1 2 1 1 =                             =                   ++ ++ ++ Y X FED ECB DBA YX FEYDX EYCXB DYBXA YX The rotation of coordinates can be written as:                     −=           1100 0cossin 0sincos 1 y x Y X ϕϕ ϕϕ We can write: [ ]                             =+++++ 1 2 1 2 1 2 1 2 1 2 1 2 1 122 Y X FED ECB DBA YXFYEXDYCXYBXA [ ]                     −                             − = 1100 0cossin 0sincos 2 1 2 1 2 1 2 1 2 1 2 1 100 0cossin 0sincos 1 y x FED ECB DBA yx ϕϕ ϕϕ ϕϕ ϕϕ [ ] 0 1 2 1 2 1 2 1 2 1 2 1 2 1 1 11 111 111 =                             = y x FED ECB DBA yx
23 SOLO CONIC SECTIONS Conic Sections – General Description (Continue – 5) Therefore we have           −                             − =                   100 0cossin 0sincos 2 1 2 1 2 1 2 1 2 1 2 1 100 0cossin 0sincos 2 1 2 1 2 1 2 1 2 1 2 1 11 111 111 ϕϕ ϕϕ ϕϕ ϕϕ FED ECB DBA FED ECB DBA       −                   − =             ϕϕ ϕϕ ϕϕ ϕϕ cossin sincos 2 1 2 1 cossin sincos 2 1 2 1 11 11 CB BA CB BA                   =                   FED ECB DBA FED ECB DBA 2 1 2 1 2 1 2 1 2 1 2 1 det 2 1 2 1 2 1 2 1 2 1 2 1 det 11 111 111 2 11 11 4 1 2 1 2 1 det 2 1 2 1 det BCA CB BA CB BA −=             =                  →> →= →< − circleorellipse parabola hyperbola BCA 0 0 0 4 1 2 and Finally we obtain: The necessary conditions for different conic sections are:
24 SOLO CONIC SECTIONS References 1. Battin R.H., “An Introduction to the Mathematics and Methods of Astrodynamics”, AIAA Education Series, AIAA, Washington. DV., 1987
January 6, 2015 25 SOLO Technion Israeli Institute of Technology 1964 – 1968 BSc EE 1968 – 1971 MSc EE Israeli Air Force 1970 – 1974 RAFAEL Israeli Armament Development Authority 1974 – 2013 Stanford University 1983 – 1986 PhD AA

More Related Content

PPTX
Conic section ppt
byFarhana Shaheen
 
PPTX
Conic Sections- Circle, Parabola, Ellipse, Hyperbola
byNaman Kumar
 
PPTX
Conic Sections
byJasminJoyceTerrado
 
PPT
Hyperbola (Advanced Algebra)
byLydelle Saringan
 
PPTX
Equation of Hyperbola
byitutor
 
PPT
Conic Section
byAshams kurian
 
PPT
Conic sectioins
byAditya Janardhanan
 
PPTX
Introduction to conic sections
byrey castro
 
Conic section ppt
byFarhana Shaheen
 
Conic Sections- Circle, Parabola, Ellipse, Hyperbola
byNaman Kumar
 
Conic Sections
byJasminJoyceTerrado
 
Hyperbola (Advanced Algebra)
byLydelle Saringan
 
Equation of Hyperbola
byitutor
 
Conic Section
byAshams kurian
 
Conic sectioins
byAditya Janardhanan
 
Introduction to conic sections
byrey castro
 

What's hot

PPTX
Grade 11 STEM (2023~2024) Hyperbolas.pptx
byAlwinCAsuncion
 
PPTX
Mehul mathematics conics
bymehuldas
 
PPT
Parabola
byheiner gomez
 
PPTX
Conic section Maths Class 11
byDevangSPSingh
 
PPT
Lesson 8 conic sections - parabola
byJean Leano
 
PPTX
Conic sections and introduction to circles
byArric Tan
 
PPTX
Lecture #6 analytic geometry
byDenmar Marasigan
 
PPTX
Conic sections
byDivyanshuTyagi8
 
PPTX
Ellipse
byitutor
 
PPTX
Maths project
byEdward Kenway
 
PPT
Math1.2
bywraithxjmin
 
PPT
Pre-Calculus 11 - Lesson no. 1: Conic Sections
byJuan Miguel Palero
 
PDF
Conic Section: Circles (Pre-Calculus).pdf
byLyndrianShalomBaclay
 
PPT
34 the ellipse
byEdcarlos Vasconcelos
 
PPTX
Hyperbolas
byHazel Llorando
 
PPT
Hyperbola
byHae Morgia
 
PPTX
Conic section
byAaryanMaheshwari
 
PDF
INTRODUCTION TO CONIC SECTIONS (BASIC CALCULUS).pdf
byLyndrianShalomBaclay
 
PPTX
Graphs of the Sine and Cosine Functions Lecture
byFroyd Wess
 
PPT
Lesson 10 conic sections - hyperbola
byJean Leano
 
Grade 11 STEM (2023~2024) Hyperbolas.pptx
byAlwinCAsuncion
 
Mehul mathematics conics
bymehuldas
 
Parabola
byheiner gomez
 
Conic section Maths Class 11
byDevangSPSingh
 
Lesson 8 conic sections - parabola
byJean Leano
 
Conic sections and introduction to circles
byArric Tan
 
Lecture #6 analytic geometry
byDenmar Marasigan
 
Conic sections
byDivyanshuTyagi8
 
Ellipse
byitutor
 
Maths project
byEdward Kenway
 
Math1.2
bywraithxjmin
 
Pre-Calculus 11 - Lesson no. 1: Conic Sections
byJuan Miguel Palero
 
Conic Section: Circles (Pre-Calculus).pdf
byLyndrianShalomBaclay
 
34 the ellipse
byEdcarlos Vasconcelos
 
Hyperbolas
byHazel Llorando
 
Hyperbola
byHae Morgia
 
Conic section
byAaryanMaheshwari
 
INTRODUCTION TO CONIC SECTIONS (BASIC CALCULUS).pdf
byLyndrianShalomBaclay
 
Graphs of the Sine and Cosine Functions Lecture
byFroyd Wess
 
Lesson 10 conic sections - hyperbola
byJean Leano
 

Similar to Conic sections

PPTX
MATHS PROJECT.pptx pappu is a ver good boy
bybaddbboy15
 
PPTX
Conic Sections (Class 11 Project)
byKushagraAgrawal46
 
PDF
conicsection-230210095242-c864bbb3.pdf m
byDreamPandey
 
PPTX
Conic Section.pptx
bySwastikPattnayak1
 
PPTX
11111Q1 - INTRODUCTION TO CONIC SECTIONS.pptx
byroselynmachecasanta
 
PPTX
Conic section
byMxolisi Creswell MNCUBE
 
PDF
conicsection-ppt-130124134216-phpapp01 (1).pdf
byRajJaiswal715327
 
PPTX
PCAL-11-Q1-0101-PF-FINAL.pptx
bySeanColadilla
 
PPTX
Conic sections
bydarencervantes
 
PDF
Cone Cutting Activity.ni.sir.ian.pls.dont
byIrisJacob2
 
PDF
Conic sections slide compatibility format doc
byविजु कर्माचार्य
 
PPT
Conic Section
bysahilsahil992
 
PDF
Conic section
byTheepakorn Boonpleng
 
PPTX
MODULE 1 - PRE CALCULUS STEM 11 CONIC SECTIONS
bylesliejoypangan121
 
PPTX
Mathematics presentation - Conic section.pptx
bynirupama74
 
PPTX
EG Presentation (CONIC SECTIONS AND INVOLUTES) (1).pptx
byTulasi72
 
PPTX
B.tech i eg u1 engineering curves
byRai University
 
PPTX
Conic Section
byRoqui Gonzaga
 
PPTX
Lecture4 Engineering Curves and Theory of projections.pptx
byKishorKumaar3
 
PPTX
Precalculus 2nd quarter (CONIC SECTIONS).pptx
byjosephinepatac1
 
MATHS PROJECT.pptx pappu is a ver good boy
bybaddbboy15
 
Conic Sections (Class 11 Project)
byKushagraAgrawal46
 
conicsection-230210095242-c864bbb3.pdf m
byDreamPandey
 
Conic Section.pptx
bySwastikPattnayak1
 
11111Q1 - INTRODUCTION TO CONIC SECTIONS.pptx
byroselynmachecasanta
 
Conic section
byMxolisi Creswell MNCUBE
 
conicsection-ppt-130124134216-phpapp01 (1).pdf
byRajJaiswal715327
 
PCAL-11-Q1-0101-PF-FINAL.pptx
bySeanColadilla
 
Conic sections
bydarencervantes
 
Cone Cutting Activity.ni.sir.ian.pls.dont
byIrisJacob2
 
Conic sections slide compatibility format doc
byविजु कर्माचार्य
 
Conic Section
bysahilsahil992
 
Conic section
byTheepakorn Boonpleng
 
MODULE 1 - PRE CALCULUS STEM 11 CONIC SECTIONS
bylesliejoypangan121
 
Mathematics presentation - Conic section.pptx
bynirupama74
 
EG Presentation (CONIC SECTIONS AND INVOLUTES) (1).pptx
byTulasi72
 
B.tech i eg u1 engineering curves
byRai University
 
Conic Section
byRoqui Gonzaga
 
Lecture4 Engineering Curves and Theory of projections.pptx
byKishorKumaar3
 
Precalculus 2nd quarter (CONIC SECTIONS).pptx
byjosephinepatac1
 

More from Solo Hermelin

PPT
5 introduction to quantum mechanics
bySolo Hermelin
 
PPT
Stabilization of linear time invariant systems, Factorization Approach
bySolo Hermelin
 
PPT
Slide Mode Control (S.M.C.)
bySolo Hermelin
 
PPT
Sliding Mode Observers
bySolo Hermelin
 
PPT
Reduced order observers
bySolo Hermelin
 
PPT
Inner outer and spectral factorizations
bySolo Hermelin
 
PPT
Keplerian trajectories
bySolo Hermelin
 
PPT
Anti ballistic missiles ii
bySolo Hermelin
 
PPT
Anti ballistic missiles i
bySolo Hermelin
 
PPT
Analytic dynamics
bySolo Hermelin
 
PPT
12 performance of an aircraft with parabolic polar
bySolo Hermelin
 
PPT
11 fighter aircraft avionics - part iv
bySolo Hermelin
 
PPT
10 fighter aircraft avionics - part iii
bySolo Hermelin
 
PPT
9 fighter aircraft avionics-part ii
bySolo Hermelin
 
PPT
8 fighter aircraft avionics-part i
bySolo Hermelin
 
PPT
6 computing gunsight, hud and hms
bySolo Hermelin
 
PPT
4 navigation systems
bySolo Hermelin
 
PPT
3 earth atmosphere
bySolo Hermelin
 
PPT
2 aircraft flight instruments
bySolo Hermelin
 
PPT
3 modern aircraft cutaway
bySolo Hermelin
 
5 introduction to quantum mechanics
bySolo Hermelin
 
Stabilization of linear time invariant systems, Factorization Approach
bySolo Hermelin
 
Slide Mode Control (S.M.C.)
bySolo Hermelin
 
Sliding Mode Observers
bySolo Hermelin
 
Reduced order observers
bySolo Hermelin
 
Inner outer and spectral factorizations
bySolo Hermelin
 
Keplerian trajectories
bySolo Hermelin
 
Anti ballistic missiles ii
bySolo Hermelin
 
Anti ballistic missiles i
bySolo Hermelin
 
Analytic dynamics
bySolo Hermelin
 
12 performance of an aircraft with parabolic polar
bySolo Hermelin
 
11 fighter aircraft avionics - part iv
bySolo Hermelin
 
10 fighter aircraft avionics - part iii
bySolo Hermelin
 
9 fighter aircraft avionics-part ii
bySolo Hermelin
 
8 fighter aircraft avionics-part i
bySolo Hermelin
 
6 computing gunsight, hud and hms
bySolo Hermelin
 
4 navigation systems
bySolo Hermelin
 
3 earth atmosphere
bySolo Hermelin
 
2 aircraft flight instruments
bySolo Hermelin
 
3 modern aircraft cutaway
bySolo Hermelin
 

Recently uploaded

PDF
Origin Of Life & Evolution || BIOLOGY || CBSE & CHSE
byVivek Kola
 
PDF
Machine Learning Lectures -- Support Vector Machine (SVM)
byZahra Sadeghi
 
PDF
Bettersize | Absolute Molecular Weight Determination of HSAs using the BeSEC
byBettersize Instruments
 
PPT
newtons-laws-of-motion.ppt explaining how
byLinditaAndoni
 
PPTX
Water treatment BOD and COD , dissolved gases
byNandhiniV90
 
PPTX
C4 cycle in plants (Hatch and Slack Pathway).pptx
byRashmiMG2
 
PPTX
Light compensation point, CO2 compensation point, Quantum yield in plants.pptx
byRashmiMG2
 
PPTX
Phytoextraction , Bioremediation . pptx
byswathin2411
 
PDF
Hematology-1-Lesson_About_Hematopoiesis_and_erythropoetin
byyunahilnaya
 
PDF
Alkane ( एल्केन ) - Notes PDF Download Hindi Medium - IRFANULLAH MEHAR.pdf
byWorld of Wisdom
 
PDF
S. Dharshini ( Msc. Microbiology) Microbial aspects and Metabolic aspects.
bydharshinisampath6
 
PPTX
Week 3 - Microbes - Pathogens & Infection (1).pptx
byEnas813292
 
PPTX
Sedimentary basins by Team Maverick.pptx
byolonabasit
 
PPTX
Bioremediation anaerobic process, sulphur, nitrate, iron reduction, hydrocarb...
byNandhiniV90
 
PPTX
DNA Structure, Damage and Repair Mechanism- Avinesh Shrestha
byAvinesh Shrestha
 
PPT
Ch04uiuuuuuuuuuuuuuuuuuuuuuukkkkkkklh.ppt
bykarzanberdawood
 
PPTX
Phytoextraction_Detailed_Presentation-1.pptx
byvidhya1172005
 
PPTX
Presentation of Bloc-Pattern-in-Flutter.pptx
bynomanali123110
 
PPT
GENETICS MODULE ONE-1. Genetic engineeri
byusmanusman4sollawu
 
PDF
Benzene ( बेंजीन ) - Organic Chemistry Notes PDF Download Slide - Irfanullah ...
byWorld of Wisdom
 
Origin Of Life & Evolution || BIOLOGY || CBSE & CHSE
byVivek Kola
 
Machine Learning Lectures -- Support Vector Machine (SVM)
byZahra Sadeghi
 
Bettersize | Absolute Molecular Weight Determination of HSAs using the BeSEC
byBettersize Instruments
 
newtons-laws-of-motion.ppt explaining how
byLinditaAndoni
 
Water treatment BOD and COD , dissolved gases
byNandhiniV90
 
C4 cycle in plants (Hatch and Slack Pathway).pptx
byRashmiMG2
 
Light compensation point, CO2 compensation point, Quantum yield in plants.pptx
byRashmiMG2
 
Phytoextraction , Bioremediation . pptx
byswathin2411
 
Hematology-1-Lesson_About_Hematopoiesis_and_erythropoetin
byyunahilnaya
 
Alkane ( एल्केन ) - Notes PDF Download Hindi Medium - IRFANULLAH MEHAR.pdf
byWorld of Wisdom
 
S. Dharshini ( Msc. Microbiology) Microbial aspects and Metabolic aspects.
bydharshinisampath6
 
Week 3 - Microbes - Pathogens & Infection (1).pptx
byEnas813292
 
Sedimentary basins by Team Maverick.pptx
byolonabasit
 
Bioremediation anaerobic process, sulphur, nitrate, iron reduction, hydrocarb...
byNandhiniV90
 
DNA Structure, Damage and Repair Mechanism- Avinesh Shrestha
byAvinesh Shrestha
 
Ch04uiuuuuuuuuuuuuuuuuuuuuuukkkkkkklh.ppt
bykarzanberdawood
 
Phytoextraction_Detailed_Presentation-1.pptx
byvidhya1172005
 
Presentation of Bloc-Pattern-in-Flutter.pptx
bynomanali123110
 
GENETICS MODULE ONE-1. Genetic engineeri
byusmanusman4sollawu
 
Benzene ( बेंजीन ) - Organic Chemistry Notes PDF Download Slide - Irfanullah ...
byWorld of Wisdom
 

Conic sections

  • 1.
  • 2.
    2 SOLO Table of Contents 2.Circle 3. Ellipse 4. Parabola 5. Hyperbola 6. Conic sections – Analytic Expressions 7. Conic sections – General Description CONIC SECTIONS 1. Conic Sections - Introduction 8. References
  • 3.
    3 SOLO A right circularcone is a cone obtained by generators (straight lines) passing through a circle, and the apex C that is situated on the normal to the circle plane and passing trough the center of the circle. β is the angle between the cone axis and the generators. CONIC SECTIONS Cutting Plane generating a "hyperbola" Right Circular Cone Cone Apex Conical Section C Cone Axis Cutting Plane generating a "parabola" Cutting Plane generating a "ellipse" Cutting Plane generating a "circle" Cutting Plane generating two "lines" α β       −= β π α 2       −< β π α 2       −> β π α 2 ( )0=α                   −> −= −< lines line po 2 2 1 2 int 2 β π α β π α β π α P F F * Cutting Plane (Hyperbola ) Right Circular Cone Hyperbola 2 Branches C β α Ellipse Parabola Cutting Plane (Ellipse) Cutting Plane (Circle) Cutting Plane (Parabola) By cutting the right circular conic by a plane we obtain different conic sections, as a function of the inclination angle α of the plane relative to the base of the conic section and the angle β between the generators and the base. The discovery of the Conical Sections is attributed to the greek Menachmus who lived around 350 B.C.. 1. Conic Sections - Introduction
  • 4.
    4 SOLO The conical sectionsare: CONIC SECTIONS 1. Circle if the cutting plane is normal to the cone axis (α=0) and is above or bellow the apex. 2. Ellipse if the cutting plane is inclined to the basis at an angle that falls short of the angle between generators to the base (α<π/2-β) (in greek word elleipsis means falls, short or leaves out. 3. Hyperbola if the cutting plane is inclined to the basis at an angle that exceeds of the angle between generators to the base (α>π/2-β)(in greek word hyperbole means excess. 4. Parabola if the cutting plane is parallel to a generator of the right circular cone (α=π/2-β) (in greek word parabole is the origin of the words parabola and parallel. 5. A point- apex (α<π/2-β), one straight line (α=π/2-β), two straight lines (α>π/2-β), if the cutting plane passes through the apex and intersects the cone basis.
  • 5.
    5 SOLO CONIC SECTIONS Circleif the cutting plane is normal to the cone axis (α=0) and is above or bellow the apex. 2. Circle
  • 6.
    6 SOLO CONIC SECTIONS 3Ellipse (α < π/2-β) To find the properties of the ellipse let introduce two spheres, with centers on the cone axis, inside the right circular cone, one the above the cutting plane and one bellow. The sphere are tangent to the right cone surfaces, along one circle each (C1 for sphere 1 and C2 for sphere 2, with centers on cone axis and parallel to cone base), and tangent to cutting plane at the points F* (sphere 1) and F (sphere 2). The center of the spheres are in the plane perpendicular to the cutting plane. They contain the cone axis, and are the intersection of this axis with the line bisecting one of the angles generated between the cone generators and intersection of perpendicular and cutting planes.
  • 7.
    7 SOLO CONIC SECTIONS Ellipse(α < π/2-β) (Continue – 1) Let draw the cone generator CP (where C is the cone apex and P is any point on the Ellipse). Since PF* is tangent to sphere 1 and PF is tangent to sphere 2, and since the tangent distances to a sphere from the same points are equal, we have: ** PQPF = PQPF = Therefore QQPQPQPFPF *** =+=+ Since Q* is on circle C1 and Q on circle C2 and on the same generator the distance Q*Q is independent on P. Ellipse (Definition 1) Ellipse is a planar curve, such that the sum of distances, from any point on the curve, to two fixed points (foci) in the plane is constant.
  • 8.
    8 SOLO CONIC SECTIONS Ellipse(α < π/2-β) (Continue – 2) One other definition is obtained by the following construction: The intersection between cutting plane and the plane containing circle C1 is called directrix 1. The intersection between cutting plane and the plane containing circle C2 is called directrix 2. The point M* on directrix 1 is on the normal from P on directrix 1 (PM* ┴ directrix 1). The point M on directrix 2 is on the normal from P on directrix 2 (PM ┴ directrix 2). The distance from the point P to the plane containing circle C1 (that contains both Q* and M*) is given by The distance from the point P to the plane containing circle C2 (that contains both Q and M) is given by ββα cos*cos*sin* ** PFPQPM PFPQ = == ββα coscossin PFPQPM PFPQ = == From those equations we obtain: Since for an ellipse α<π/2-β → sinα<sin(π/2-β) we have: β α cos sin * * == PM PF PM PF 1 cos sin : <= β α e e - eccentricity
  • 9.
    9 SOLO CONIC SECTIONS Ellipse(α < π/2-β) (Continue – 3) We obtained: 1 cos sin * * <=== e PM PF PM PF β α P F Q* Q Cutting Plane Right Circular Cone Sphere2 Tangent to Cone at Q & Cutting Plane at F Sphere1 Tangent to Cone at Q* & Cutting Plane at F* Cone Appex Circle C1 on the Cone & Sphere1 Circle C2 on the Cone & Sphere2 R1 R2 C M* M Directrix 2 Directrix 1 α β F* PQPF = ** PQPF = constQQ PQPQ PFPF = =+ =+ * * * β β α cos cos sin PF PQ PM = = β β α cos* cos* sin* PF PQ PM = = 1: cos sin * * <=== e PM PF PM PF β α Ellipse (Definition 2) Ellipse is a planar curve, such that the ratio of distances, from any point on the curve, to a fixed point F* (focus 1) and to the line directrix1 and ratio of distances to a second fixed point F and the second line directrix 2 (parallel to directrix1) are constant and equal to e < 1. The focci F* and F are between the two directrices, where F* is closer to directrix 1 and F to directrix 2. The proof given here was supplied in 1822 by the Belgian mathematician Germinal P. Dandelin (1794-1847)
  • 10.
    10 SOLO CONIC SECTIONS 4.Parabola (α = π/2-β) To find the properties of the parabola let introduce a sphere, with center on the cone axis, inside the right circular cone, above the cutting plane. The sphere is tangent to the right cone surfaces, along one circle C with center on cone axis and parallel to cone base, and tangent to cutting plane at point F. Let draw the cone generator CP (where C is the cone apex and P is any point on the Parabola). CP is tangent to the sphere at point Q (on circle C). Since PF is tangent to the sphere, and all tangents from the same point are equal PF = PQ. Let perform the following construction:The intersection between cutting plane and the plane containing circle C is called directrix. The point M on directrix is on the normal from P on directrix (PM ┴ directrix). The distance from the point P to the plane containing circle C (that contains both Q and M) is given by ββα coscossin PFPQPM PFPQ = ==
  • 11.
    11 SOLO CONIC SECTIONS Parabola(α = π/2-β) (Continue – 1) P F Q Cutting Plane Right Circular Cone SphereTangent to Cone at Q* & Cuting Plane at F* Cone Apex Plane Containin g the Circle Tangent to Cone & Sphere Circle Tangent to Cone & Sphere β βπα −= 2/ M Directrix PQPF = β β α cos cos sin PF PQ PM = = e PM PF === :1 cos sin β α The distance from the point P to the plane containing circle C (that contains both Q and M) is given by ββα coscossin PFPQPM PFPQ = == β α cos sin = PM PF From those equations we obtain: Since for a parabola α = π/2-β → sinα = sin(π/2-β)=cos β we have: e - eccentricity 1 cos sin : == β α e e - eccentricity Parabola (Definition) Parabola is a planar curve, such that the distances, from any point on the curve, to a fixed point (focus) and to the line directrix are equal.
  • 12.
    12 SOLO CONIC SECTIONS 5.Hyperbola (α > π/2-β) To find the properties of the hyperbola let introduce two spheres, with centers on the cone axis, inside the right circular cone, one the above the apex and one bellow. The sphere are tangent to the right cone surfaces, along one circle each (C1 for sphere 1 and C2 for sphere 2, with centers on cone axis and parallel to cone base), and tangent to cutting plane at the points F* (sphere 1) and F (sphere 2). The center of the spheres are in the plane perpendicular to the cutting plane. They contain the cone axis, and are the intersection of this axis with the line bisecting one of the angles generated between the cone generators and intersection of perpendicular and cutting planes.
  • 13.
    13 SOLO CONIC SECTIONS Hyperbola(α > π/2-β) (Continue – 1) Let draw the cone generator CP (where C is the cone apex and P is any point on the Hyperbola). Since PF* is tangent to sphere 1 and PF is tangent to sphere 2, and since the tangent distances to a sphere from the same points are equal, we have: ** PQPF = PQPF = Therefore *** QCQPQPQPFPF =−=− Since Q* is on circle C1 and Q on circle C2 and on the same generator the distance Q*Q is independent on P. P F F* Q Cutting Plane Right Circular Cone Sphere1 Tangent to Cone & Cuting Plane at F* Cone Apex Circle on the Sphere2 & Cone Sphere2 Tangent to Cone & Cuting Plane at F Circle on the Sphere1 & Cone Conical Section Conical Section C Q* Cone Axis Hyperbola (Definition 1) Hyperbola is a planar curve, such that the difference of distances, from any point on the curve, to two fixed points (foci) in the plane is constant. Hyperbola has two branches.
  • 14.
    14 SOLO CONIC SECTIONS Hyperbola(α > π/2-β) (Continue – 2) One other definition is obtained by the following construction: The intersection between cutting plane and the plane containing circle C1 is called directrix 1. The intersection between cutting plane and the plane containing circle C2 is called directrix 2. The point M* on directrix 1 is on the normal from P on directrix 1 (PM* ┴ directrix 1). The point M on directrix 2 is on the normal from P on directrix 2 (PM ┴ directrix 2). The distance from the point P to the plane containing circle C1 (that contains both Q* and M*) is given by The distance from the point P to the plane containing circle C2 (that contains both Q and M) is given by ββα cos*cos*sin* ** PFPQPM PFPQ = == ββα coscossin PFPQPM PFPQ = == From those equations we obtain: Since for an ellipse α>π/2-β → sinα>sin(π/2-β) we have: β α cos sin * * == PM PF PM PF 1 cos sin : >= β α e e - eccentricity P F F* Q Cutting Plane Right Circular Cone Sphere1 Tangent to Cone & Cuting Plane at F* Cone Apex Sphere2 Tangent to Cone & Cuting Plane at F Circle C1 on the Sphere1 & Cone Conical Section Conical Section Q* CCircle C2 on the Sphere2 & Cone PQPF = ** PQPF = constQCQ PQPQ PFPF = =− =− * * * β β α cos cos sin PF PQ PM = = β β α cos* cos* sin* PF PQ PM = = ( )βπα −> 2/ β Directrix1 Directrix2M M* α 1: cos sin * * >=== e PM PF PM PF β α
  • 15.
    15 SOLO CONIC SECTIONS Hyperbola(α < π/2-β) (Continue – 3) We obtained: 1 cos sin * * >=== e PM PF PM PF β α Hyperbola (Definition 2) Hyperbola is a planar curve, such that the ratio of distances, from any point on the curve, to a fixed point F* (focus 1) and to the line directrix1 and ratio of distances to a second fixed point F and the second line directrix 2 (parallel to directrix1) are constant and equal to e > 1. The focci F* and F are between the two directrices, where F* is closer to directrix 1 and F to directrix 2. P F F* Q Cutting Plane Right Circular Cone Sphere1 Tangent to Cone & Cuting Plane at F* Cone Apex Sphere2 Tangent to Cone & Cuting Plane at F Circle C1 on the Sphere1 & Cone Conical Section Conical Section Q* CCircle C2 on the Sphere2 & Cone PQPF = ** PQPF = constQCQ PQPQ PFPF = =− =− * * * β β α cos cos sin PF PQ PM = = β β α cos* cos* sin* PF PQ PM = = ( )βπα −> 2/ β Directrix1 Directrix2M M* α 1: cos sin * * >=== e PM PF PM PF β α
  • 16.
    16 SOLO CONIC SECTIONS 6.Conic Sections – Analytic Expressions ( ) ( ) aycxycx 22222 =++±+− ( ) ( ) 2222 2 ycxaycx +−−=++± ( ) ( ) ( ) 2222222 44 ycxaycxaycx +−−+−+=++ ( ) 22 ycxa a xc +−−=− 2222 2 22 22 ycxcxaxc a cx ++−=+− 222 2 22 2 cay a ca x −=+ −122 2 2 2 = − + ca y a x cacab b y a x >←−=←=+ 222 2 2 2 2 1 caacb b y a x <←−=←=− 222 2 2 2 2 1 012 2 2 2 =←=+ c a y a x ellipse hyperbola circle Start with ellipse and hyperbola definitions:
  • 17.
    17 SOLO CONIC SECTIONS ConicSections – Analytic Expressions (Continue) Ellipse and Hyperbola Polar Representations: Φ 0Φ P F *F x y r c2 Φ 0Φ P F x y r p 2/p Ellipse & Hyperbola Parabola Parabola Polar Representations: ( )( ) ( ) arrcr 2sincos2 0 222 0 =Φ−Φ+Φ−Φ+± ( ) 222 0 2 44cos44 rararcrc +−=+Φ−Φ+ ( ) ( ) ( ) a c e e ea a c a c a r =← Φ−Φ+ − = Φ−Φ+       − = 0 2 0 2 2 cos1 1 cos1 1 ( )0cos Φ−Φ−= rpr ( ) 1 cos1 0 =← Φ−Φ+ = e e p r or
  • 18.
    18 SOLO CONIC SECTIONS 7.Conic Sections – General Description Let perform a rotation of coordinates: 022 =+++++ FYEXDYCXYBXA ϕϕ ϕϕ cossin sincos yxY yxX +−= += ( ) 0cossinsincos sincoscossincossin cossin2cossin cossin2sincos 2222 2222 2222 =++−++ −++− −++ ++ FEyxEyDxD yxByBxB yxCyCxC yxAyAxA ϕϕϕϕ ϕϕϕϕϕϕ ϕϕϕϕ ϕϕϕϕ Choose φ such that the coefficient of xy is zero: ( ) ( ) 0sincoscossin2 22 =−−− ϕϕϕϕ BAC ( ) AC B − =02tan ϕ
  • 19.
    19 SOLO CONIC SECTIONS ConicSections – General Description (Continue – 1) 0cossinsincos cossincossin cossin sincos 0000 00 2 00 2 ) 22 0 22 0 22 0 22 =++−++ +− ++ + FEyxEyDxD yBxB yCxC yAxA ϕϕϕϕ ϕϕϕϕ ϕϕ ϕϕ ( ) ( ) ( ) ( ) 0cossinsincos cossincossincossinsincos 0000 2 00) 2 0 22 000 2 0 2 =+++−+ +++−+ FyEDxED yBCAxBCA ϕϕϕϕ ϕϕϕϕϕϕϕϕ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 cossincossin2 cossin cossinsincos2 sincos cossincossin2 cossin cossincossin cossinsincos2 sincos cossinsincos 2 00) 2 0 2 00 2 000 2 0 2 00 2 00) 2 0 2 00 00) 2 0 2 2 000 2 0 2 00 000 2 0 2 1 1 =+         ++ + −        −+ − −         ++ + ++++         −+ − +−+ F BCA ED BCA ED BCA ED yBCA BCA ED xBCA C A ϕϕϕϕ ϕϕ ϕϕϕϕ ϕϕ ϕϕϕϕ ϕϕ ϕϕϕϕ ϕϕϕϕ ϕϕ ϕϕϕϕ       We obtain or or
  • 20.
    20 SOLO CONIC SECTIONS ConicSections – General Description (Continue – 2) Let define ( )000 2 0 2 1 cossinsincos: ϕϕϕϕ BCAA −+= ( )00) 2 0 2 1 cossincossin: ϕϕϕϕ BCAC ++= 001 001 cossin: sincos: ϕϕ ϕϕ EDE EDD += −= We can see that CACA +=+ 11 1. If A1 ≠ 0 & C1 ≠ 0. We define ( ) ( ) ( ) ( ) 2 00) 2 0 2 00 2 000 2 0 2 00 1 cossincossin2 cossin cossinsincos2 sincos :         ++ + −      −+ − −= ϕϕϕϕ ϕϕ ϕϕϕϕ ϕϕ BCA ED BCA ED FF If A1, C1, F1 ≠ 0 do not have the same algebraic sign, than the equation is an equation of an ellipse, circle or hyperbola 1 1 1 2 A D xx += 1 1 1 2C E yy += The equation becomes: 01 2 11 2 11 =++ FyCxA If sign A1 = sign C1 ≠ sign F1 & A1 = C1 → circle If sign A1 = sign C1 ≠ sign F1 & A1 ≠ C1 → ellipse If sign A1 ≠ sign C1 → hyperbola
  • 21.
    21 SOLO CONIC SECTIONS ConicSections – General Description (Continue – 3) 2. If A1 = 0 , C1 ≠ 0 & D1 ≠ 0. We define 1 2 1 1 1 2 : D C E F xx       − += 1 1 1 2 : C E yy += Parabola011 2 11 =+ xDyCThe equation becomes: Parabola011 2 11 =+ yExAThe equation becomes: 3. If A1 ≠ 0 , C1 = 0 & E1 ≠ 0. We define 1 1 1 2 : A D xx += 1 1 1 1 2 : E A D F yy       − +=
  • 22.
    22 SOLO CONIC SECTIONS ConicSections – General Description (Continue – 4) The equation can be rewritten as022 =+++++ FYEXDYCXYBXA [ ] [ ] 0 1 2 1 2 1 2 1 2 1 2 1 2 1 1 2 1 2 1 2 1 2 1 2 1 2 1 1 =                             =                   ++ ++ ++ Y X FED ECB DBA YX FEYDX EYCXB DYBXA YX The rotation of coordinates can be written as:                     −=           1100 0cossin 0sincos 1 y x Y X ϕϕ ϕϕ We can write: [ ]                             =+++++ 1 2 1 2 1 2 1 2 1 2 1 2 1 122 Y X FED ECB DBA YXFYEXDYCXYBXA [ ]                     −                             − = 1100 0cossin 0sincos 2 1 2 1 2 1 2 1 2 1 2 1 100 0cossin 0sincos 1 y x FED ECB DBA yx ϕϕ ϕϕ ϕϕ ϕϕ [ ] 0 1 2 1 2 1 2 1 2 1 2 1 2 1 1 11 111 111 =                             = y x FED ECB DBA yx
  • 23.
    23 SOLO CONIC SECTIONS ConicSections – General Description (Continue – 5) Therefore we have           −                             − =                   100 0cossin 0sincos 2 1 2 1 2 1 2 1 2 1 2 1 100 0cossin 0sincos 2 1 2 1 2 1 2 1 2 1 2 1 11 111 111 ϕϕ ϕϕ ϕϕ ϕϕ FED ECB DBA FED ECB DBA       −                   − =             ϕϕ ϕϕ ϕϕ ϕϕ cossin sincos 2 1 2 1 cossin sincos 2 1 2 1 11 11 CB BA CB BA                   =                   FED ECB DBA FED ECB DBA 2 1 2 1 2 1 2 1 2 1 2 1 det 2 1 2 1 2 1 2 1 2 1 2 1 det 11 111 111 2 11 11 4 1 2 1 2 1 det 2 1 2 1 det BCA CB BA CB BA −=             =                  →> →= →< − circleorellipse parabola hyperbola BCA 0 0 0 4 1 2 and Finally we obtain: The necessary conditions for different conic sections are:
  • 24.
    24 SOLO CONIC SECTIONS References 1.Battin R.H., “An Introduction to the Mathematics and Methods of Astrodynamics”, AIAA Education Series, AIAA, Washington. DV., 1987
  • 25.
    January 6, 201525 SOLO Technion Israeli Institute of Technology 1964 – 1968 BSc EE 1968 – 1971 MSc EE Israeli Air Force 1970 – 1974 RAFAEL Israeli Armament Development Authority 1974 – 2013 Stanford University 1983 – 1986 PhD AA