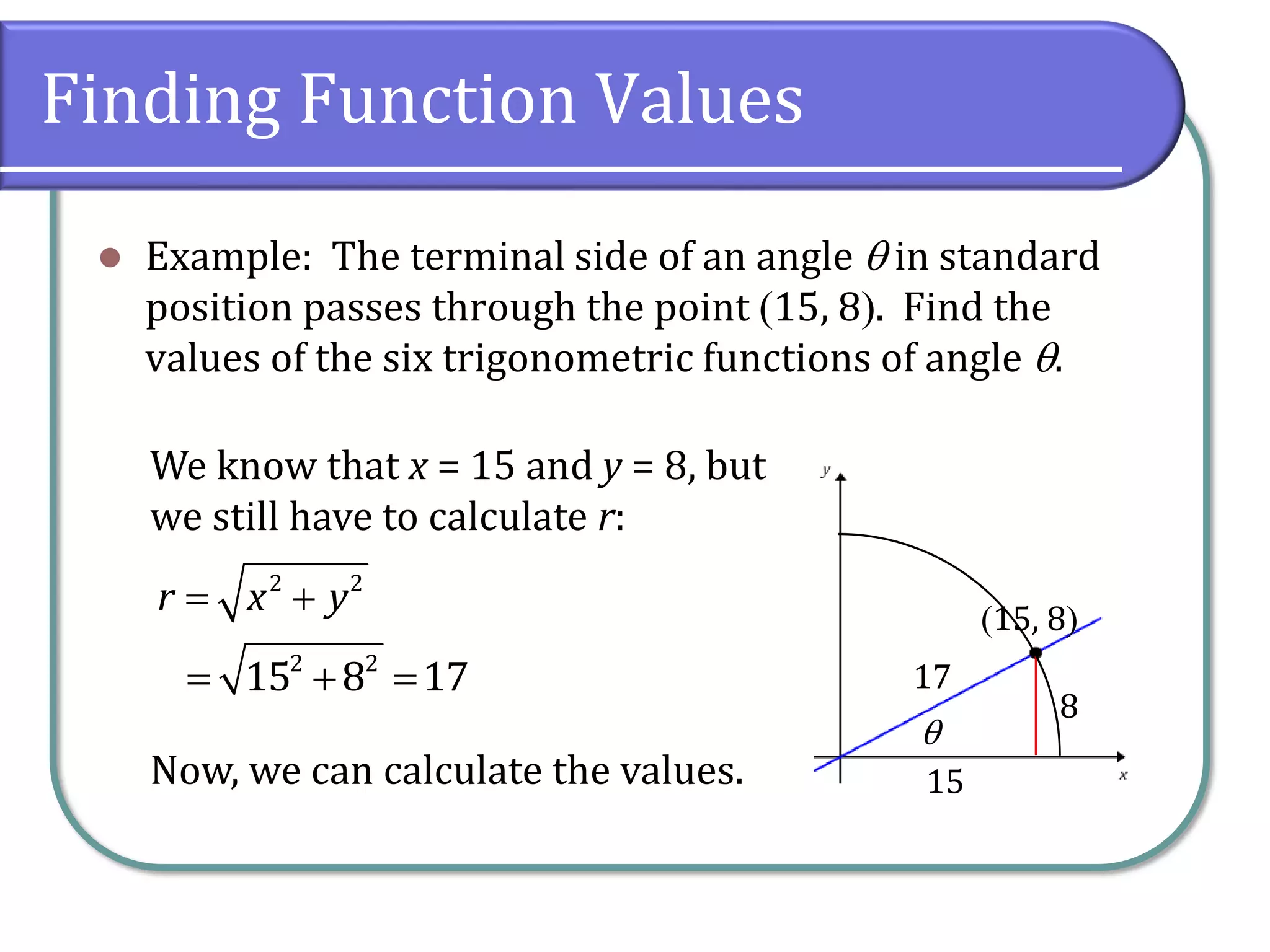
This document covers trigonometric functions, including the definitions and calculations of the six functions for given angles. It explains key concepts such as finding function values from points on the unit circle, identifying quadrantal angles, and determining which quadrant an angle resides in based on its sine, cosine, and tangent values. Additionally, it discusses relationships among these functions, such as their reciprocals and how knowing one function allows for the calculation of others.

1. 5.2 Trigonometric Functions
Chapter 5 – Trigonometric Functions

2. Concepts and Objectives
⚫ Definitions of Trigonometric Functions
⚫ Find the values of the six trigonometric functions of
angle .
⚫ Find the function values of quadrantal angles.
⚫ Identify the quadrant of a given angle.
⚫ Find the other function values given one value and
the quadrant

3. Trigonometric Ratio Review
⚫ In Geometry, we learned that for any given right triangle,
there are special ratios between the sides.
A
opposite
adjacent
=
opposite
sin
hypotenuse
A
=
adjacent
cos
hypotenuse
A
=
opposite
tan
adjacent
A

4. Trigonometric Functions
⚫ Consider a circle centered at the origin with radius r:
⚫ The equation for this circle is x2 + y2 = r2
⚫ A point (x, y) on the circle creates a right triangle whose
sides are x, y, and r.
⚫ The trig ratios are now (x, y)
r
x
y=sin
y
r

=cos
x
r

=tan
y
x


5. Trigonometric Functions
⚫ There are three other ratios in addition to the three we
already know : cosecant, secant, and cotangent.
⚫ These ratios are the reciprocals of the original three:
(x, y)
r
x
y
= =
1
csc
sin
r
y


= =
1
sec
cos
r
x


= =
1
cot
tan
x
y



6. Finding Function Values
⚫ Example: The terminal side of an angle  in standard
position passes through the point (15, 8). Find the
values of the six trigonometric functions of angle .
(15, 8)


7. Finding Function Values
⚫ Example: The terminal side of an angle  in standard
position passes through the point (15, 8). Find the
values of the six trigonometric functions of angle .
8
15
(15, 8)

We know that x = 15 and y = 8, but
we still have to calculate r:
Now, we can calculate the values.
= +2 2
r x y
= + =2 2
15 8 17 17

8. Finding Function Values
⚫ Example: The terminal side of an angle  in standard
position passes through the point (15, 8). Find the
values of the six trigonometric functions of angle .
8
15
(15, 8)

17
= =
8
sin
17
y
r

= =
15
cos
17
x
r

= =
8
tan
15
y
x

= =
17
csc
8
r
y

= =
17
sec
15
r
x

= =
15
cot
8
x
y


9. Introducing the Unit Circle
⚫ Recall that angles in standard position whose terminal
sides lie on the x-axis or y-axis (90°, 180°, 270°, etc.) are
called quadrantal angles.
⚫ To find function values of quandrantal angles easily, we
⚫ Notice that at the quadrantal
angle points x and y are either
0, 1, or –1 (r is always 1).
use a circle with a radius of 1, which
is called a unit circle.
90
(0, 1)
(0, –1)
270
180
(–1, 0)
0/360
(1, 0)

10. Values of Quadrantal Angles
⚫ Example: Find the values of the six trigonometric
functions for an angle of 270°.

11. Values of Quadrantal Angles
⚫ Example: Find the values of the six trigonometric
functions for an angle of 270°.
At 270°, x = 0, y = –1, r = 1.
−
 = = −
1
sin270 1
1
 = =
0
cos270 0
1
−
 = =
1
tan270 undefined
0
(0, –1)

12. Values of Quadrantal Angles
⚫ Example: Find the values of the six trigonometric
functions for an angle of 270°.
At 270°, x = 0, y = –1, r = 1.
 = = −
−
1
csc270 1
1
 = =
1
sec270 undefined
0
 = =
−
0
cot270 0
1
(0, –1)

13. Identifying an Angle’s Quadrant
⚫ To identify the quadrant of an angle given certain
conditions, note the following:
⚫ In the first quadrant, x and y are both positive.
⚫ In QII, x is negative and y is positive.
⚫ In QIII, both are negative.
⚫ In QIV, x is positive and y is
IVIII
II I
(+,+)(–,+)
(–,–)
negative.
(+,–)

14. Identifying an Angle’s Quadrant
⚫ Example: Identify the quadrant (or possible quadrants)
of an angle  that satisfies the given conditions.
a) sin  > 0, tan  < 0 b) cos  < 0, sec  < 0

15. Identifying an Angle’s Quadrant
⚫ Example: Identify the quadrant (or possible quadrants)
of an angle  that satisfies the given conditions.
a) sin  > 0, tan  < 0 b) cos  < 0, sec  < 0
I, II II, IV
II
II, III II, III
II, III

16. Finding Other Function Values
⚫ We can consider the six functions as three pairs of
related functions: sine and cosecant, cosine and secant,
and tangent and cotangent. Because these pairs are
reciprocals of each other, if we know one function, we
can find the other by inverting or “flipping” the function.
⚫ Example: Find cos θ, given that
5
sec
3
=
3
cos
5
 =

17. Finding Other Function Values
⚫ Example: Find sin θ, given that
12
csc
2
 = −
2
sin
12
2
2 3
 = −
= −
12 4 3
2 3
=
=

18. Finding Other Function Values
⚫ Example: Find sin θ, given that
12
csc
2
 = −
2
sin
12
2 1
2 3 3
 = −
= − = −
12 4 3
2 3
=
=

19. Finding Other Function Values
⚫ Example: Find sin θ, given that
12
csc
2
 = −
2
sin
12
2 1
2 3 3
1 3
3 3
 = −
= − = −
 
= −  
 
12 4 3
2 3
=
=
Rationalize the
denominator.

20. Finding Other Function Values
⚫ Example: Find sin θ, given that
12
csc
2
 = −
2
sin
12
2 1
2 3 3
1 3 3
33 3
 = −
= − = −
 
= − = − 
 
12 4 3
2 3
=
=
Rationalize the
denominator.

21. Finding Other Function Values
⚫ Because the functions are all defined in terms of x, y, and
r, if we know one function, with a little work, we can find
any of the others.
⚫ Example: Find sin θ and cos θ, given that and
θ is in quandrant III.
4
tan
3
 =

22. Finding Other Function Values
⚫ Because the functions are all defined in terms of x, y, and
r, if we know one function, with a little work, we can find
any of the others.
⚫ Example: Find sin θ and cos θ, given that and
θ is in quandrant III.
Recall that and
If θ is in QIII, then both x and y are negative.
4
tan
3
 =
tan , sin , cos ,
y y x
x r r
  = = = 2 2 2
x y r+ =

23. Finding Other Function Values
⚫ Example: Find sin θ and cos θ, given that and
θ is in quandrant III.
Therefore, y = –4, x = –3, and
4
tan
3
 =
( ) ( )
2 2
3 4 5r = − + − =
4
sin
5
y
r
 = = −
3
cos
5
x
r
 = = −

24. Classwork
⚫ College Algebra
⚫ Page 513: 30-46, page 501: 58-68 (evens)