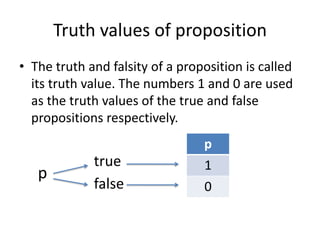
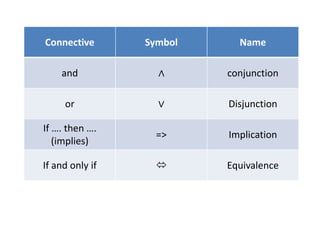
This document defines key concepts in logic and propositions: 1) A proposition is a statement that is either true or false, such as "Dogs have six legs" or "2+3=5". 2) The truth value of a proposition is either 1 (true) or 0 (false). 3) Two propositions are equivalent if they have the same truth value. The negation of a proposition, denoted by p', is its opposite truth value. 4) A compound proposition combines two or more simple propositions using logical connectives like "and", "or", or "if/then".

1. Logic

2. Propositions
• An assertion which is definitely either true or
false is called a proposition, shown by the letters
p, q, r, s, ….
• Examples:
• Dogs with six legs.
• 2+3=5
• Come here.
• Who is that?
• The triangle is negative.

3. Truth values of proposition
• The truth and falsity of a proposition is called
its truth value. The numbers 1 and 0 are used
as the truth values of the true and false
propositions respectively.
p
true 1
p
false 0

4. p q
1
1 1
1 q
0 1 0
p
1 0 1
0 q
0 0 0

5. Equivalent propositions
• Two propositions p and q have the same truth
value they are said to be equivalent
propositions, denoted as

6. Negation of a proposition
• The negation of a proposition p is denoted by
p’ . The following table provides some
information about negation.
p p’ Some symbols negation
1 0 = ≠
0 1 > ≤
≥ <

7. Compound Propositions
• A proposition which is formed two or more
propositions by using connective words is called a
compound proposition.
Connective Words:
And
Or
Then
If and only if

8. Connective Symbol Name
and ∧ conjunction
or ∨ Disjunction
If …. then ….
=> Implication
(implies)
If and only if  Equivalence

9. Conjunction ∧
• A compound proposition of p and q formed
using the connective word “and” is called
conjunction of p and q, written as p∧q.
• The conjunction of p and q is true if both p
and q are true otherwise it is false.
p q p∧q
1 1 1
1 0 0
0 1 0
0 0 0

10. Disjunction ∨
• A compound proposition of p and q formed
using the connective word “or” is called
disjunction of p and q, written as p∨q.
• The disjunction of p and q is false if both p
and q are false otherwise it is true.
p q p∨q
1 1 1
1 0 1
0 1 1
0 0 0

11. Common properties of ∧ and ∨

12. Common properties of ∧ and ∨

13. Common properties of ∧ and ∨