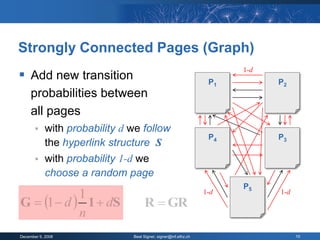
The document provides an overview of the PageRank algorithm, developed by Larry Page and Sergey Brin at Stanford University as part of a search engine project. It explains the mechanics of calculating PageRank, including how it factors in the quantity and quality of linking pages, as well as its implications for website development and SEO practices. The document also highlights the various factors that influence a page's ranking, both positive and negative, and discusses tool options for tracking PageRank and optimizing web content.

1. Google PageRank
Prof. Beat Signer
<bsigner@vub.ac.be>
Department of Computer Science
Vrije Universiteit Brussel
http://www.beatsigner.com
December 9, 2008

2. Overview
 History of PageRank
 PageRank algorithm
 Examples
 Implications for website development
December 9, 2008 Beat Signer, signer@inf.ethz.ch 2

3. History of PageRank
 Developed as part of an academic
project at Stanford University
 research platform to aid under- Larry Page Sergey Brin
standing of large-scale web data
and enable researches to easily
experiment with new search technologies
 Larry Page and Sergey Brin worked on the project
about a new kind of search engine (1995-1998) which
finally led to a functional prototype called Google
December 9, 2008 Beat Signer, signer@inf.ethz.ch 3

4. Web Search Until 1998
 Find all documents using a query term
 use information retrieval (IR) solutions
 ranking based on "on-page factors"
 problem: poor quality of search results (order)
 Page and Brin proposed to compute the
absolute qualtity of a page (PageRank)
 based on the number and quality of pages
linking to a page (votes)
December 9, 2008 Beat Signer, signer@inf.ethz.ch 4

5. PageRank P1 P5 P7 P8
R1 R5 R7 R8
P2 P3 P4 P6
R2 R3 R4 R6
 A page has a high PageRank R if
 there are many pages linking to it
 or, if there are some pages with a high PageRank
linking to it
 Total score = IR score x PageRank
December 9, 2008 Beat Signer, signer@inf.ethz.ch 5

6. PageRank Algorithm
R( Pj )
R( Pi )  
Pj Bi Lj
P1 P2
1.5
1 1.5
1
 where
 Bi is the set of pages
that link to page Pi P3
 Lj is the number of 0.75
1
outgoing links for page Pj
December 9, 2008 Beat Signer, signer@inf.ethz.ch 6

7. Matrix Representation
 Let us define a hyperlink P1 P2
matrix H
1 L j if Pj  Bi
H ij  
 0 otherwise
0 1 2 1 
and R  RPi 
P3
H  1 0 0
 
 R  HR 0 1 2 0 
 
R is an eigenvector of H
with eigenvalue 1
December 9, 2008 Beat Signer, signer@inf.ethz.ch 7

8. Matrix Representation ...
 We can use the power method to find R
t 1
R  HR t
0 1 2 1 
For our example H  1 0 0
 
0 1 2 0 
 
this results in R  2 2 1 or 0.4 0.4 0.2
December 9, 2008 Beat Signer, signer@inf.ethz.ch 8

9. Dangling Pages
 Problem with pages P1 P2
C
that have no outbound
links (P2)
0 0  C
H  and R  0 0
1 0
0 1 2  0 1 2
C  and S  H  C   
 0 1 2 1 1 2
December 9, 2008 Beat Signer, signer@inf.ethz.ch 9

10. Strongly Connected Pages (Graph)
1-d
 Add new transition P1 P2
probabilities between
all pages
 with probability d we follow
P4 P3
the hyperlink structure S
 with probability 1-d we
choose a random page
P5
1-d 1-d
G  1  d  1  dS
1
R  GR
n
December 9, 2008 Beat Signer, signer@inf.ethz.ch 10

11. G  1  d  1  dS
1
Examples n
A2
0.37
A1 A3
0.26 0.37
December 9, 2008 Beat Signer, signer@inf.ethz.ch 11

12. G  1  d  1  dS
1
Examples ... n
A2 B2
0.185 0.185
A1 A3 B1 B3
0.13 0.185 0.13 0.185
P A  0.5 PB   0.5
December 9, 2008 Beat Signer, signer@inf.ethz.ch 12

13. G  1  d  1  dS
1
Examples ... n
A2 B2
0.14 0.20
A1 A3 B1 B3
0.10 0.14 0.22 0.20
P A  0.38 PB   0.62
December 9, 2008 Beat Signer, signer@inf.ethz.ch 13

14. G  1  d  1  dS
1
Examples ... n
A2 B2
0.23 0.095
A1 A3 B1 B3
0.3 0.18 0.10 0.095
P A  0.71 PB   0.29
December 9, 2008 Beat Signer, signer@inf.ethz.ch 14

15. G  1  d  1  dS
1
Examples ... n
A2 B2
0.24 0.07
A1 A3 B1 B3
0.35 0.18 0.09 0.07
P A  0.77 PB   0.23
December 9, 2008 Beat Signer, signer@inf.ethz.ch 15

16. G  1  d  1  dS
1
Examples ... n
A2 B2
0.17 0.06
A1 A3 B1 B3
0.33 0.175 0.08 0.06
A4 PB   0.20
P A  0.80
0.125
December 9, 2008 Beat Signer, signer@inf.ethz.ch 16

17. Implications for Website Development
 First make sure that your page gets indexed
 on-page factors
 Think about your site's internal link structure
 create many internal links for important pages
 be "careful" about where to put outgoing links
 Increase the number of pages
 Ensure that webpages are addressed consistently
 http://www.vub.ac.be  http://www.vub.ac.be/index.php
 Make sure that you get links from good websites
December 9, 2008 Beat Signer, signer@inf.ethz.ch 17

18. Consistent Addressing of Webpages
December 9, 2008 Beat Signer, signer@inf.ethz.ch 18

19. Search Engine Optimisations (SEO)
 Internet marketing has become a big business
 white hat and black hat optimisations
 Bad ranking or removal from index can cost a
company a lot of money
 e.g. supplemental index ("Google hell")
December 9, 2008 Beat Signer, signer@inf.ethz.ch 19

20. Black Hat Optimisations (Don'ts)
 Link farms
 Spamdexing in guestbooks, Wikipedia etc.
 "solution": <a rel="nofollow" href="…">…</a>
 Doorway pages (cloaking)
 e.g. BMW Germany and Ricoh Germany banned in
February 2006
 Selling/buying links
 ...
December 9, 2008 Beat Signer, signer@inf.ethz.ch 20

21. On-Page Factors (Speculative)
 It is assumed that there are over 200 on-page
and off-page factors
 Positive factors
 keyword in title tag
 keyword in URL
 keyword in domain name
 quality of HTML code
 page freshness (occasional changes)
 …
December 9, 2008 Beat Signer, signer@inf.ethz.ch

22. On-Page Factors (Speculative) …
 Negative factors
 links to "bad neighbourhood"
 over optimisation penalty (keyword stuffing)
 text with same colour as background (hidden content)
 automatic redirects via the refresh meta tag
 any copyright violations
 …
December 9, 2008 Beat Signer, signer@inf.ethz.ch

23. Off-Page Factors (Speculative)
 Positive factors
 high PageRank
 anchor text of inbound links
 links from authority sites (Hilltop algorithm)
 listed in DMOZ (ODP) and Yahoo directories
 site age (stability)
 domain expiration date
 …
December 9, 2008 Beat Signer, signer@inf.ethz.ch

24. Off-Page Factors (Speculative) …
 Negative factors
 link buying (fast increasing number of inbound links)
 link farms
 cloaking (different pages for spider and user)
 limited (temporal) availability of site
 links from bad neighbourhood?
 competitor attack (e.g. duplicate content)?
 …
December 9, 2008 Beat Signer, signer@inf.ethz.ch

25. Tools
 Google toolbar
 PageRank information not frequently updated
 Google webmaster tools
 meta description issues
 title tag issues
 non-indexable content issues
 number and URLs of indexed pages
 number and URLs of inbound/outbound links
 ...
December 9, 2008 Beat Signer, signer@inf.ethz.ch 25

26. Questions
 Is PageRank fair?
 What about Google's power and influence?
December 9, 2008 Beat Signer, signer@inf.ethz.ch 26

27. Conclusions
 PageRank algorithm
 absolute quality of a page based on incoming links
 random surfer model
 computed as eigenvector of Google matrix G
 Implications for website development and SEO
 PageRank is just one (important) factor
December 9, 2008 Beat Signer, signer@inf.ethz.ch 27

28. References
 The PageRank Citation Ranking: Bringing Order
to the Web, L. Page, S. Brin, R. Motwani and
T. Winograd, January 1998
 The Anatomy of a Large-Scale Hypertextual
Web Search Engine, S. Brin and L. Page,
Computer Networks and ISDN Systems, 30(1-7),
April 1998
December 9, 2008 Beat Signer, signer@inf.ethz.ch

29. References …
 PageRank Uncovered, C. Ridings and
M. Shishigin, September 2002
 PageRank Calculator,
http://www.webworkshop.net/pagerank_
calculator.php
December 9, 2008 Beat Signer, signer@inf.ethz.ch 29