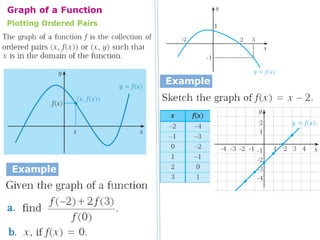
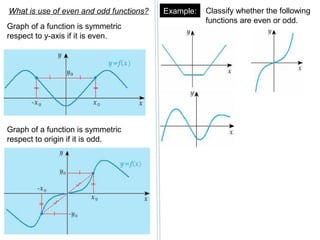
This document discusses key concepts related to functions including: - The domain of a function is the set of all real numbers for which the expression is defined as a real number. - Two functions are equal if and only if their expressions and domains are equal. - An even function satisfies f(-x) = f(x) and an odd function satisfies f(-x) = -f(x). Graphs of even functions are symmetric to the y-axis and odds are symmetric to the origin. 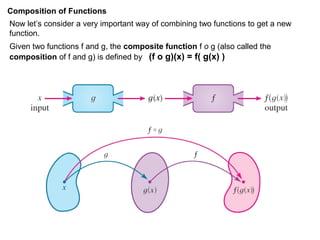- Composition of functions f o g is defined as (f o g)(x) = f(g(x)). Inverse functions satisfy y = f(x) if and only if x =

1. FUNCTIONS

8. The Domain of a Function
Example:
The domain is the set of all real numbers
for which the expression is defined as a
real number.
f(x) = 2x + 3
D=R
g(x) = 2x + 3
D=R
Example:
f(x) = g(x)
Example:
1
f (x ) =
x −4
D = R – {4}
f (x ) = x
D = R+
g(x) = x
f (x ) =
5
f (x ) = 2 − x
2x − 6
x
f (x ) = 2
f (x ) = x 2 − 4
x −9
f (x ) =
Equal Functions
Two functions are equal if and only if their
expressions and domains are equal.
2
x
x
D=R
f(x) ≠ g(x)
D = R – {0}
Even and Odd Function
A function is called even if
f(-x) = f(x)
A function is called odd if
f(-x) = -f(x)
Example:
State whether each of the following
functions are even or odd function.
f(x) = 3x2 + 4
h(x) = 2x3
g(x) = x
m(x) = x3 – 1

9. What is use of even and odd functions?
Graph of a function is symmetric
respect to y-axis if it is even.
Graph of a function is symmetric
respect to origin if it is odd.
Example:
Classify whether the following
functions are even or odd.

10. Vertical Line Test: A graph is a function if every
vertical line intersects the graph at most one
point.
Example:
Find f + g, f - g, f·g, and f/g
Operations on Functions:
Homework: Page 53 check yourself 13
Homework: Page 53 check yourself 13

11. Composition of Functions
Now let’s consider a very important way of combining two functions to get a new
function.
Given two functions f and g, the composite function f o g (also called the
composition of f and g) is defined by (f o g)(x) = f( g(x) )

12. Example:

13. Inverse Functions
Horizontal Line Test
One-to-One Function
A function f is one-to-one if and only if
A function f with domain D and range R is a every horizontal line intersects the graph of
f in at most one point.
one-to-one function if either of the
following equivalent conditions is satisfied:
(1) Whenever a≠b in D, then f(a) ≠ f(b) in R.
(2) Whenever f(a) = f(b) in R, then a=b in D.
Example:
Example:
Check whether the following
functions are one-to-one.
f(x) = 3x + 1
g(x) = x2 - 3
h(x) = 1 - x

14. Inverse Function
Let f be a one-to-one function with domain
D and range R. A function g with domain R
and range D is the inverse function of f,
provided the following condition is true for
every x in D and every y in R:
y = f(x)
The two graphs are reflections of each
other through the line y = x , or are
symmetric with respect to this line.
if and only if x = g(y)
How to find inverse of a function
Solve the equation x = f(y) for y.
f(x) = 3x + 7