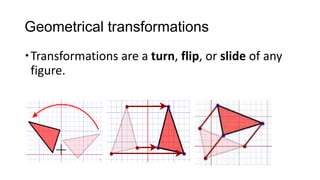
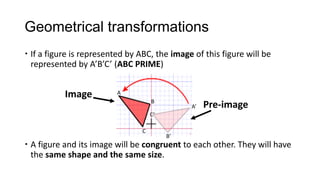
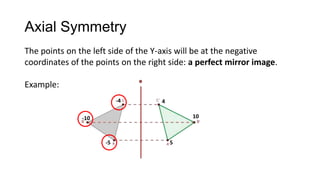
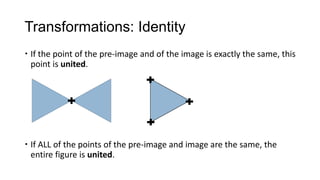
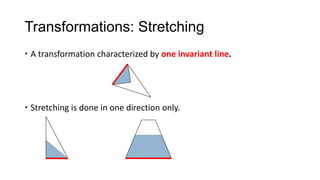
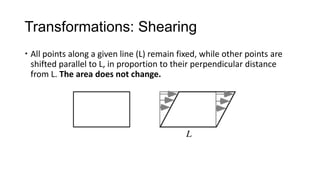
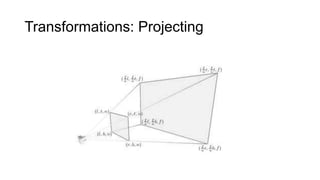
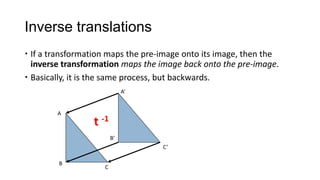
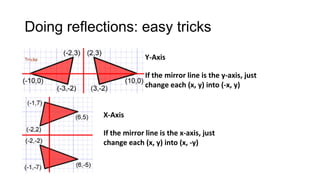
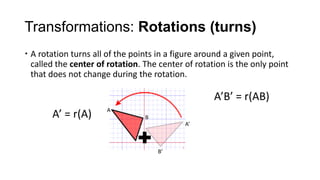
1) Geometrical transformations include turns, flips, or slides of figures that result in a congruent image. 2) Translations (slides) move every point of a figure by the same displacement vector, resulting in a figure pointing in the same direction. Reflections (flips) produce an image with the opposite orientation across a mirror line. 3) Rotations turn all points of a figure around a central point, with the center of rotation unchanged. A 180-degree rotation is a half turn.

1. Geometry
Graziadei/Leone
2O & 2A
October 29, 2012

2. Geometrical transformations
Transformations are a turn, flip, or slide of any
figure.

3. Geometrical transformations
 If a figure is represented by ABC, the image of this figure will be
represented by A’B’C’ (ABC PRIME)
Image A
B
A’ Pre-image
C’
C
B’
 A figure and its image will be congruent to each other. They will have
the same shape and the same size.

4. Transformations: Translations (slides)
 A translation is a transformation whose points are all the same
relative distance from the pre-image and which is pointing in the
same direction.

5. Writing translations
 If we want to say that the shape gets moved 30 Units in the "X"
direction, and 40 Units in the "Y" direction, we can write:
 This says "all the x and y coordinates will become x+30 and y+40"

6. Transformations: Reflections (flips)
 A reflection is an isometry in which a figure and its image have opposite
orientations
37 33 33 37
20 20
 An isometry is when the distance between any two points in the pre-
image must be the same as the distance between the images of the two
points.

7. Doing reflections: easy tricks
Tricks Y-Axis
If the mirror line is the y-axis, just
change each (x, y) into (-x, y)
X-Axis
If the mirror line is the x-axis, just
change each (x, y) into (x, -y)

8. Symmetry
 If a line is drawn down the middle of an object, both sides would be
identical.

9. Axial Symmetry
The points on the left side of the Y-axis will be at the negative
coordinates of the points on the right side: a perfect mirror image.
Example:
-4 4
-10 10
-5 5

10. Transformations: Rotations (turns)
 A rotation turns all of the points in a figure around a given point,
called the center of rotation. The center of rotation is the only point
that does not change during the rotation.
A’B’ = r(AB)
A
A’ = r(A) B
A’
B’

11. Transformations: Rotation
 180-degree turn = half turn
 A positive angle rotation is when one figure is rotated counter-
clockwise
 A negative angle rotation is when the figure is rotated clockwise.

12. Transformations: Identity
 If the point of the pre-image and of the image is exactly the same, this
point is united.
 If ALL of the points of the pre-image and image are the same, the
entire figure is united.

13. Transformations: Expansions &
Contractions
 Produces an image that is the same shape as the original, but it is a
different size.
 Expansion if the scale factor is greater than 1
 Contraction is the scale factor is between 0 and 1

14. Transformations: Stretching
 A transformation characterized by one invariant line.
 Stretching is done in one direction only.

15. Similar or congruent?
congruent
congruent
similar
similar

16. Transformations: Shearing
 All points along a given line (L) remain fixed, while other points are
shifted parallel to L, in proportion to their perpendicular distance
from L. The area does not change.

17. Transformations: Projecting

18. Inverse translations
 If a transformation maps the pre-image onto its image, then the
inverse transformation maps the image back onto the pre-image.
 Basically, it is the same process, but backwards.
A’
A
t -1
B’
C’
B
C